2.6二次函数与一元二次方程 说课课件(共36张PPT)2023-2024学年北师大版九年级数学上册
文档属性
| 名称 | 2.6二次函数与一元二次方程 说课课件(共36张PPT)2023-2024学年北师大版九年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-21 21:26:42 | ||
图片预览








文档简介
(共36张PPT)
题
说
课
课
二次函数与一元二次方程
敬请您批评指正!
汇报人:
1
教材分析
2
学情分析
5
教法与学法
6
教学过程
目
录
教学目标
3
4
特色说明
2
4
教材分析
本节课是北师大版数学九年级下册第二章《二次函数》第五节第一课时的内容。本节课是在学生对一元二次方程以及二次函数图象、性质的学习后进行的综合学习。学生已具备了相应的学习经验,如画二次函数图象、判别一元二次方程根的情况等。
通过本节课的学习认识到求二次函数与x轴(y=h)交点的横坐标问题可以转化为一元二次方程的问题来解决,学好本节课有助于学生增强在解决中考二次函数综合题中的读图、作图、析图能力,突出体现了数形结合思想。十大核心概念在本节课中突出培养的是几何直观、运算能力。
教材分析
学情分析
教学目标
教法与学法分析
教学过程
特色说明
学情分析
教材分析
学情分析
教学目标
教法与学法分析
教学过程
特色说明
知识基础:学生对二次函数的图象及其性质和一元二次方程的解的情况都有所了解,特别的,八年级时学生已经了解到了一次函数和一元一次方程的解之间的关系,因而,对于本节所要学习的二次函数与一元二次方程之间的关系可以类比学习。
知识障碍:本节课的主要目的在于建立二次函数与一元二次方程之间的联系,部分同学一开始理解时可能存在困难,缺乏在题目中“翻译、转化”的能力
教学目标
教材分析
学情分析
教学目标
教法与学法分析
教学过程
特色说明
理解二次函数与x 轴交点的个数与一元二次方程的根的关系,理解何时方程有两个不等的实根、两个相等的实根和没有实根。
理解一元二次方程的根就是二次函数与y =h 交点的横坐标。
经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系。
1
2
3
难点
教学重难点
教材分析
学情分析
教学目标
教法与学法分析
教学过程
特色说明
把握二次函数图象与x轴(或y=h)交点与一元二次方程的根的关系 。
重点
应用一元二次方程根的判别式及求根公式来对二次函数及其图象进行进一步的理解。
教法与学法分析
教材分析
学情分析
教学目标
教法与学法分析
教学过程
特色说明
启发
发现
讨论
动手
操作
小组合作
以学生为主体,以问题为主线,以质疑为特征
1.二次函数与x轴的交点与一元二次方程的根有什么关系?
2.二次函数与y=h的交点与一元二次方程的根有什么关系?
3.还有哪些交点类型?在哪些地方考察?
小组讨论要求
时间:5分钟;小组长组织本组组员进行合作交流;
每个人充分表达自己的观点;能提出新的数学问题.
【合作辩疑】
1.二次函数与x轴的交点与一元二次方程的根有什么关系?
2.二次函数与y=h的交点与一元二次方程的根有什么关系?
3.还有哪些交点类型?在哪些地方考察?
y=kx+b
令y=0
解有关x的一元一次方程:kx+b=0
总结:一次函数y=kx+b与x轴交点横坐标
即为方程kx+b=0的解
二次函数有没有类似的过程和结论成立呢?
(二次函数y=ax +bx+c与x轴交点横坐标
即为方程ax +bx+c=0的解?)
结合导案知识探究,说出你的结论.
类比猜想
回顾:结合导案相关链接思考,如何求一次函数y=kx+b与x轴的交点坐标?
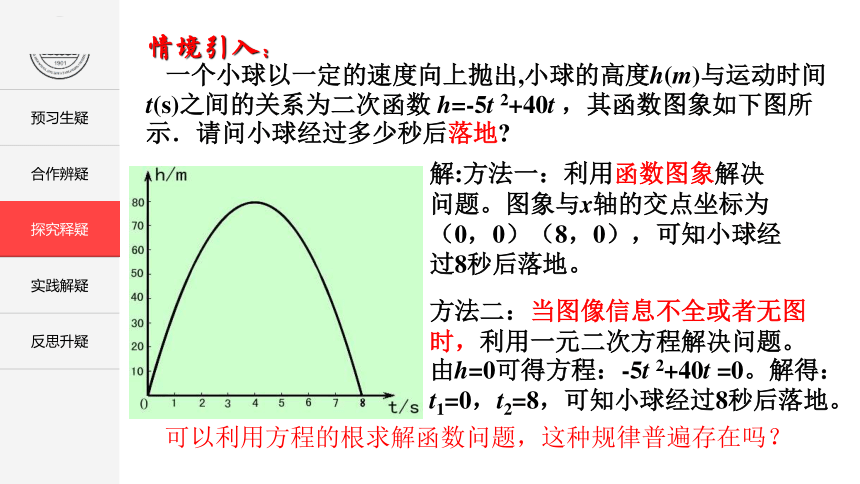
一个小球以一定的速度向上抛出,小球的高度h(m)与运动时间t(s)之间的关系为二次函数 h=-5t 2+40t ,其函数图象如下图所示.请问小球经过多少秒后落地
解:方法一:利用函数图象解决问题。图象与x轴的交点坐标为(0,0)(8,0),可知小球经过8秒后落地。
方法二:当图像信息不全或者无图时,利用一元二次方程解决问题。由h=0可得方程:-5t 2+40t =0。解得:t1=0,t2=8,可知小球经过8秒后落地。
可以利用方程的根求解函数问题,这种规律普遍存在吗?
情境引入:
【探究活动一】
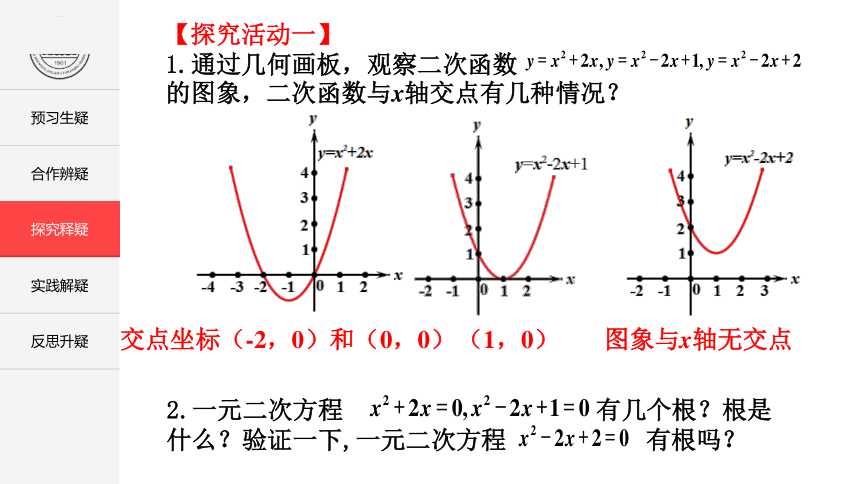
1.通过几何画板,观察二次函数 的图象,二次函数与x轴交点有几种情况?
(1,0)
图象与x轴无交点
交点坐标(-2,0)和(0,0)
2.一元二次方程 有几个根?根是什么?验证一下,一元二次方程 有根吗?
二次函数 的图象与x轴有几个交点?
一元二次方程
有几个根?
与x轴有2个交点:
(-2,0)、(0,0)
方程有2个根:
二次函数
的图象与x轴有几个交点?
一元二次方程
有几个根?
与x轴有1个交点:(1,0)
方程有两个相等的根:
二次函数
的图象与x轴有几个交点?
一元二次方程
有几个根?
与x轴没有交点
方程没有实数根
结合这3个图,你发现了与二次函数与x轴的交点与一元二次方程的根有什么规律?
再找几个例子,用几何画板演示,体会规律的一般性
二次函数 y=ax +bx+c
的图象与x轴有几个交点?
一元二次方程 ax +bx+c=0
有几个根?
二次函数的图象和x轴的交点 一元二次方程的根 一元二次方程根的判别式
有两个交点
有两个不等的实数根
有一个交点
有两个相等的
实数根
没有交点
没有实数根
要求y=ax +bx+c与x轴交点
令y=0
解有关x的一元二次方程:ax +bx+c=0
若有解,解即为交点横坐标
你发现二次函数y=ax +bx+c的图象和x轴交点的坐标与一元二次方程ax +bx+c=0的根有什么关系 你能说明理由吗?
答:有交点.
令y=0,则-x2+4x-3=0,解得
令x=0,则y=-3,
1.二次函数与x轴的交点与一元二次方程的根有什么关系?
2.二次函数与y=h的交点与一元二次方程的根有什么关系?
3.还有哪些交点类型?在哪些地方考察?
y= -x +4x-3
-1= -x +4x-3
在函数y= -x +4x-3上求满足y=-1的点的横坐标
y=-x +4x-3与y=-1的交点横坐标,即为一元二次方程 -x +4x-3=-1的解
y=-1
满足条件的点既在二次函数上,又在y=-1上;
所以,这个点为两个图象交点
一元二次方程ax2+bx+c=h的根是函数y=ax2+bx+c的图象和
直线y=h交点坐标的横坐标.
质疑问题2:二次函数与y=h的交点与一元二次方程的根有什么关系?
情境引入中的小球上抛问题中,h=-5t 2+40t ,何时小球离地面的高度是60m,你是如何知道的,你有几种方法
(2)方法二:利用方程:把h=60 代入得 -5t2+40t=60
解得t1=2 t2=6
h
t
2
4
6
8
20
40
0
60
80
100
(1)方法一:利用图像
问题解决
小球能达到100米的高度吗?
2.还可以怎样做?
1.顶点式:
h
t
2
4
6
8
20
40
0
60
80
100
1.二次函数与x轴的交点与一元二次方程的根有什么关系?
2.二次函数与y=h的交点与一元二次方程的根有什么关系?
3.还有哪些交点类型?在哪些地方考察?
y= -x +4x-3
x= -x +4x-3
在函数y= -x +4x-3上求满足y=x的点的横坐标
y=x
y=-x +4x-3与y=x的交点横坐标,即为一元二次方程
-x +4x-3=x的解
满足条件的点既在二次函数上,又在y=x上;
所以,这个点为两个图象交点
跟踪练习
解:令
整理得
解方程得
图像有两个交点
1.若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x轴的交点情况是( )
A.无交点 B.只有一个交点
C.有两个交点 D.不能确定
C
2.已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方
程ax2+bx+c=0的解是 .
x
y
0
5
x1=0,x2=5
3.二次函数y=x2+2x﹣8图象与x轴的交点坐标为__________.二次函数y=x2+2x﹣8图象与y=-8的交点坐标为__________.
二次函数y=x2+2x﹣8图象与 y=-x+4 的交点坐标为___________.
4.链接中考
2. 二次函数与一元二次方程的关系
y=ax2+bx+c
ax2+bx+c=h
y取定值h
方程的根
交点的横坐标
与直线y=h
1.二次函数y=ax2+bx+c与x轴交点个数的确定
二次函数
的图象和x轴交点
一元二次方程
的根
从一般到特殊
从特殊到一般
数形结合的思想
(数)
(形)
结合
转化
结合
转化
数量关系
空间形式
代数特征
几何问题代数化
精确刻画
直观形象
几何意义
代数问题几何化
数缺形时少直观,
形少数时难入微,
数形结合百般好,
隔离分家万事休。
———华罗庚
一、采用质疑式课堂模式,注重对学生思维的培养。数学课堂,要以学生为主体,使学生带着问题走进课堂,探究合作解决问题,注重批判性思维的培养。对于学生提出的问题,处理讲究有层次,有梯度,有深度,注重数学思想方法的引导。
二、运用几何画板等软件直观演示,突破难点。紧扣数与形两条线,以形助数,以数解形,学生通过类比猜想、图形验证、说明推理,有效地突破了难点;及时小结,注重升华;紧密链接中考,注意拓展延伸和上下链接。
教材分析
学情分析
教学目标
教法与学法分析
教学过程
特色说明
数学是思维的体操。怎样培养学生的核心素养,我认为目标就是:即便学生将来忘记了所学的知识,却会在将来感激数学课堂带来的思维灵动。
这就是我们数学教师的使命与价值。
教材分析
学情分析
教学目标
教法与学法分析
教学过程
特色说明
THANKS!
恳请各位老师批评指正!
题
说
课
课
二次函数与一元二次方程
敬请您批评指正!
汇报人:
1
教材分析
2
学情分析
5
教法与学法
6
教学过程
目
录
教学目标
3
4
特色说明
2
4
教材分析
本节课是北师大版数学九年级下册第二章《二次函数》第五节第一课时的内容。本节课是在学生对一元二次方程以及二次函数图象、性质的学习后进行的综合学习。学生已具备了相应的学习经验,如画二次函数图象、判别一元二次方程根的情况等。
通过本节课的学习认识到求二次函数与x轴(y=h)交点的横坐标问题可以转化为一元二次方程的问题来解决,学好本节课有助于学生增强在解决中考二次函数综合题中的读图、作图、析图能力,突出体现了数形结合思想。十大核心概念在本节课中突出培养的是几何直观、运算能力。
教材分析
学情分析
教学目标
教法与学法分析
教学过程
特色说明
学情分析
教材分析
学情分析
教学目标
教法与学法分析
教学过程
特色说明
知识基础:学生对二次函数的图象及其性质和一元二次方程的解的情况都有所了解,特别的,八年级时学生已经了解到了一次函数和一元一次方程的解之间的关系,因而,对于本节所要学习的二次函数与一元二次方程之间的关系可以类比学习。
知识障碍:本节课的主要目的在于建立二次函数与一元二次方程之间的联系,部分同学一开始理解时可能存在困难,缺乏在题目中“翻译、转化”的能力
教学目标
教材分析
学情分析
教学目标
教法与学法分析
教学过程
特色说明
理解二次函数与x 轴交点的个数与一元二次方程的根的关系,理解何时方程有两个不等的实根、两个相等的实根和没有实根。
理解一元二次方程的根就是二次函数与y =h 交点的横坐标。
经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系。
1
2
3
难点
教学重难点
教材分析
学情分析
教学目标
教法与学法分析
教学过程
特色说明
把握二次函数图象与x轴(或y=h)交点与一元二次方程的根的关系 。
重点
应用一元二次方程根的判别式及求根公式来对二次函数及其图象进行进一步的理解。
教法与学法分析
教材分析
学情分析
教学目标
教法与学法分析
教学过程
特色说明
启发
发现
讨论
动手
操作
小组合作
以学生为主体,以问题为主线,以质疑为特征
1.二次函数与x轴的交点与一元二次方程的根有什么关系?
2.二次函数与y=h的交点与一元二次方程的根有什么关系?
3.还有哪些交点类型?在哪些地方考察?
小组讨论要求
时间:5分钟;小组长组织本组组员进行合作交流;
每个人充分表达自己的观点;能提出新的数学问题.
【合作辩疑】
1.二次函数与x轴的交点与一元二次方程的根有什么关系?
2.二次函数与y=h的交点与一元二次方程的根有什么关系?
3.还有哪些交点类型?在哪些地方考察?
y=kx+b
令y=0
解有关x的一元一次方程:kx+b=0
总结:一次函数y=kx+b与x轴交点横坐标
即为方程kx+b=0的解
二次函数有没有类似的过程和结论成立呢?
(二次函数y=ax +bx+c与x轴交点横坐标
即为方程ax +bx+c=0的解?)
结合导案知识探究,说出你的结论.
类比猜想
回顾:结合导案相关链接思考,如何求一次函数y=kx+b与x轴的交点坐标?
一个小球以一定的速度向上抛出,小球的高度h(m)与运动时间t(s)之间的关系为二次函数 h=-5t 2+40t ,其函数图象如下图所示.请问小球经过多少秒后落地
解:方法一:利用函数图象解决问题。图象与x轴的交点坐标为(0,0)(8,0),可知小球经过8秒后落地。
方法二:当图像信息不全或者无图时,利用一元二次方程解决问题。由h=0可得方程:-5t 2+40t =0。解得:t1=0,t2=8,可知小球经过8秒后落地。
可以利用方程的根求解函数问题,这种规律普遍存在吗?
情境引入:
【探究活动一】
1.通过几何画板,观察二次函数 的图象,二次函数与x轴交点有几种情况?
(1,0)
图象与x轴无交点
交点坐标(-2,0)和(0,0)
2.一元二次方程 有几个根?根是什么?验证一下,一元二次方程 有根吗?
二次函数 的图象与x轴有几个交点?
一元二次方程
有几个根?
与x轴有2个交点:
(-2,0)、(0,0)
方程有2个根:
二次函数
的图象与x轴有几个交点?
一元二次方程
有几个根?
与x轴有1个交点:(1,0)
方程有两个相等的根:
二次函数
的图象与x轴有几个交点?
一元二次方程
有几个根?
与x轴没有交点
方程没有实数根
结合这3个图,你发现了与二次函数与x轴的交点与一元二次方程的根有什么规律?
再找几个例子,用几何画板演示,体会规律的一般性
二次函数 y=ax +bx+c
的图象与x轴有几个交点?
一元二次方程 ax +bx+c=0
有几个根?
二次函数的图象和x轴的交点 一元二次方程的根 一元二次方程根的判别式
有两个交点
有两个不等的实数根
有一个交点
有两个相等的
实数根
没有交点
没有实数根
要求y=ax +bx+c与x轴交点
令y=0
解有关x的一元二次方程:ax +bx+c=0
若有解,解即为交点横坐标
你发现二次函数y=ax +bx+c的图象和x轴交点的坐标与一元二次方程ax +bx+c=0的根有什么关系 你能说明理由吗?
答:有交点.
令y=0,则-x2+4x-3=0,解得
令x=0,则y=-3,
1.二次函数与x轴的交点与一元二次方程的根有什么关系?
2.二次函数与y=h的交点与一元二次方程的根有什么关系?
3.还有哪些交点类型?在哪些地方考察?
y= -x +4x-3
-1= -x +4x-3
在函数y= -x +4x-3上求满足y=-1的点的横坐标
y=-x +4x-3与y=-1的交点横坐标,即为一元二次方程 -x +4x-3=-1的解
y=-1
满足条件的点既在二次函数上,又在y=-1上;
所以,这个点为两个图象交点
一元二次方程ax2+bx+c=h的根是函数y=ax2+bx+c的图象和
直线y=h交点坐标的横坐标.
质疑问题2:二次函数与y=h的交点与一元二次方程的根有什么关系?
情境引入中的小球上抛问题中,h=-5t 2+40t ,何时小球离地面的高度是60m,你是如何知道的,你有几种方法
(2)方法二:利用方程:把h=60 代入得 -5t2+40t=60
解得t1=2 t2=6
h
t
2
4
6
8
20
40
0
60
80
100
(1)方法一:利用图像
问题解决
小球能达到100米的高度吗?
2.还可以怎样做?
1.顶点式:
h
t
2
4
6
8
20
40
0
60
80
100
1.二次函数与x轴的交点与一元二次方程的根有什么关系?
2.二次函数与y=h的交点与一元二次方程的根有什么关系?
3.还有哪些交点类型?在哪些地方考察?
y= -x +4x-3
x= -x +4x-3
在函数y= -x +4x-3上求满足y=x的点的横坐标
y=x
y=-x +4x-3与y=x的交点横坐标,即为一元二次方程
-x +4x-3=x的解
满足条件的点既在二次函数上,又在y=x上;
所以,这个点为两个图象交点
跟踪练习
解:令
整理得
解方程得
图像有两个交点
1.若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x轴的交点情况是( )
A.无交点 B.只有一个交点
C.有两个交点 D.不能确定
C
2.已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方
程ax2+bx+c=0的解是 .
x
y
0
5
x1=0,x2=5
3.二次函数y=x2+2x﹣8图象与x轴的交点坐标为__________.二次函数y=x2+2x﹣8图象与y=-8的交点坐标为__________.
二次函数y=x2+2x﹣8图象与 y=-x+4 的交点坐标为___________.
4.链接中考
2. 二次函数与一元二次方程的关系
y=ax2+bx+c
ax2+bx+c=h
y取定值h
方程的根
交点的横坐标
与直线y=h
1.二次函数y=ax2+bx+c与x轴交点个数的确定
二次函数
的图象和x轴交点
一元二次方程
的根
从一般到特殊
从特殊到一般
数形结合的思想
(数)
(形)
结合
转化
结合
转化
数量关系
空间形式
代数特征
几何问题代数化
精确刻画
直观形象
几何意义
代数问题几何化
数缺形时少直观,
形少数时难入微,
数形结合百般好,
隔离分家万事休。
———华罗庚
一、采用质疑式课堂模式,注重对学生思维的培养。数学课堂,要以学生为主体,使学生带着问题走进课堂,探究合作解决问题,注重批判性思维的培养。对于学生提出的问题,处理讲究有层次,有梯度,有深度,注重数学思想方法的引导。
二、运用几何画板等软件直观演示,突破难点。紧扣数与形两条线,以形助数,以数解形,学生通过类比猜想、图形验证、说明推理,有效地突破了难点;及时小结,注重升华;紧密链接中考,注意拓展延伸和上下链接。
教材分析
学情分析
教学目标
教法与学法分析
教学过程
特色说明
数学是思维的体操。怎样培养学生的核心素养,我认为目标就是:即便学生将来忘记了所学的知识,却会在将来感激数学课堂带来的思维灵动。
这就是我们数学教师的使命与价值。
教材分析
学情分析
教学目标
教法与学法分析
教学过程
特色说明
THANKS!
恳请各位老师批评指正!
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
