数学人教A版(2019)选择性必修第一册2.3.3点到直线的距离公式(共17张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.3.3点到直线的距离公式(共17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 404.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-21 21:50:23 | ||
图片预览





文档简介
(共17张PPT)
2.3.3 点到直线的距离公式
第二章 直线和圆的方程
2.2 直线的方程
高二数学备课组
1、两点间距离公式
特别地,点P(x,y)与坐标原点的距离是
平面内两点P1(x1,y1),P2(x2,y2),
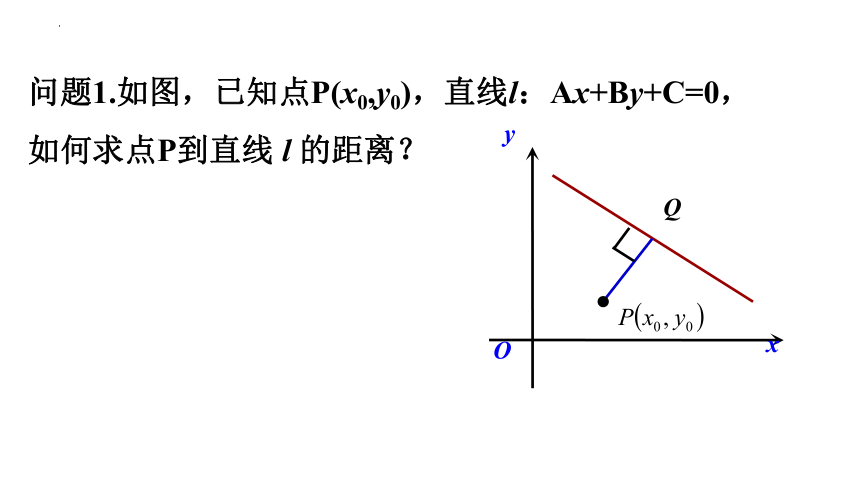
问题1.如图,已知点P(x0,y0),直线l:Ax+By+C=0,如何求点P到直线 l 的距离?
x
y
O
Q
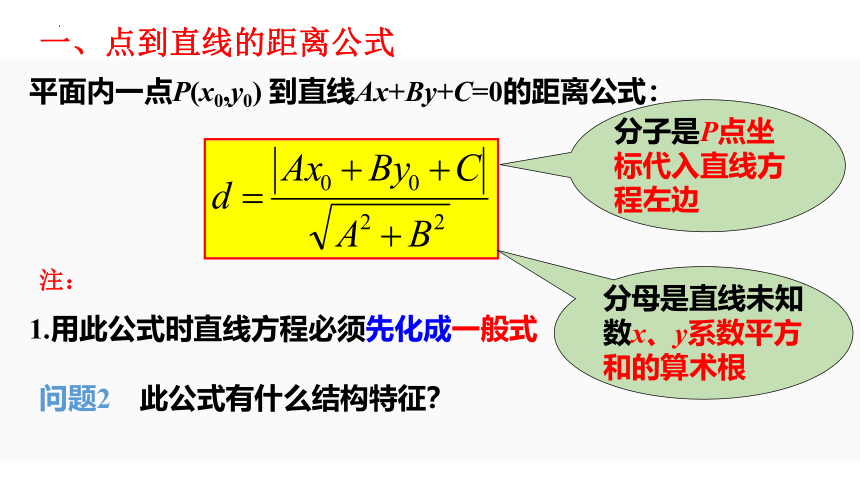
平面内一点P(x0,y0) 到直线Ax+By+C=0的距离公式:
分子是P点坐标代入直线方程左边
分母是直线未知数x、y系数平方和的算术根
1.用此公式时直线方程必须先化成一般式
注:
一、点到直线的距离公式
问题2 此公式有什么结构特征?
解:
题型一 求点到直线的距离
题型一 求点到直线的距离
课本77页
例2已知点P(2,-1),求过点P且与原点距离为2的直线l的方程.
题型二 点到直线距离的应用
例2 已知点P(2,-1),求过点P且与原点距离为2的直线l的方程.
当直线l的斜率不存在时,直线l的方程为x=2,符合题意;
当直线l的斜率存在时,设直线l的方程为y+1=k(x-2),即kx-y-2k-1=0,
所以直线l的方程为3x-4y-10=0.
故直线l的方程为x=2或3x-4y-10=0.
题型二 点到直线距离的应用
练3.已知直线l经过点P(0,2),且A(1,1),B(-3,1)两点到直线l的距离相等,求直线l的方程.
题型二 点到直线距离的应用
题型二 点到直线距离的应用
练4.求垂直于直线x+3y-5=0且与点P(-1,0)的距离是 的直线l的方程.
题型二 点到直线距离的应用
题型二 点到直线距离的应用
例3 已知点A(1,3), B(3,1), C(-1,0),求△ABC的面积.
题型二 点到直线距离的应用
练6.已知点A(-1,3), B(-3,0), C(1,2),求△ABC的面积.
练6.已知点A(-1,3), B(-3,0), C(1,2),求△ABC的面积.
题型二 点到直线距离的应用
课堂小结
平面上两点P1(x1,y1), P2(x2,y2)的距离:
点 到直线 的距离:
THANKS
2.3.3 点到直线的距离公式
第二章 直线和圆的方程
2.2 直线的方程
高二数学备课组
1、两点间距离公式
特别地,点P(x,y)与坐标原点的距离是
平面内两点P1(x1,y1),P2(x2,y2),
问题1.如图,已知点P(x0,y0),直线l:Ax+By+C=0,如何求点P到直线 l 的距离?
x
y
O
Q
平面内一点P(x0,y0) 到直线Ax+By+C=0的距离公式:
分子是P点坐标代入直线方程左边
分母是直线未知数x、y系数平方和的算术根
1.用此公式时直线方程必须先化成一般式
注:
一、点到直线的距离公式
问题2 此公式有什么结构特征?
解:
题型一 求点到直线的距离
题型一 求点到直线的距离
课本77页
例2已知点P(2,-1),求过点P且与原点距离为2的直线l的方程.
题型二 点到直线距离的应用
例2 已知点P(2,-1),求过点P且与原点距离为2的直线l的方程.
当直线l的斜率不存在时,直线l的方程为x=2,符合题意;
当直线l的斜率存在时,设直线l的方程为y+1=k(x-2),即kx-y-2k-1=0,
所以直线l的方程为3x-4y-10=0.
故直线l的方程为x=2或3x-4y-10=0.
题型二 点到直线距离的应用
练3.已知直线l经过点P(0,2),且A(1,1),B(-3,1)两点到直线l的距离相等,求直线l的方程.
题型二 点到直线距离的应用
题型二 点到直线距离的应用
练4.求垂直于直线x+3y-5=0且与点P(-1,0)的距离是 的直线l的方程.
题型二 点到直线距离的应用
题型二 点到直线距离的应用
例3 已知点A(1,3), B(3,1), C(-1,0),求△ABC的面积.
题型二 点到直线距离的应用
练6.已知点A(-1,3), B(-3,0), C(1,2),求△ABC的面积.
练6.已知点A(-1,3), B(-3,0), C(1,2),求△ABC的面积.
题型二 点到直线距离的应用
课堂小结
平面上两点P1(x1,y1), P2(x2,y2)的距离:
点 到直线 的距离:
THANKS
