【名师制作】2014-2015学年华师大版八年级数学下册 同步跟踪训练:16-4 零指数与负整指数(8页,考点+分析+点评)
文档属性
| 名称 | 【名师制作】2014-2015学年华师大版八年级数学下册 同步跟踪训练:16-4 零指数与负整指数(8页,考点+分析+点评) |

|
|
| 格式 | zip | ||
| 文件大小 | 43.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-14 08:46:00 | ||
图片预览

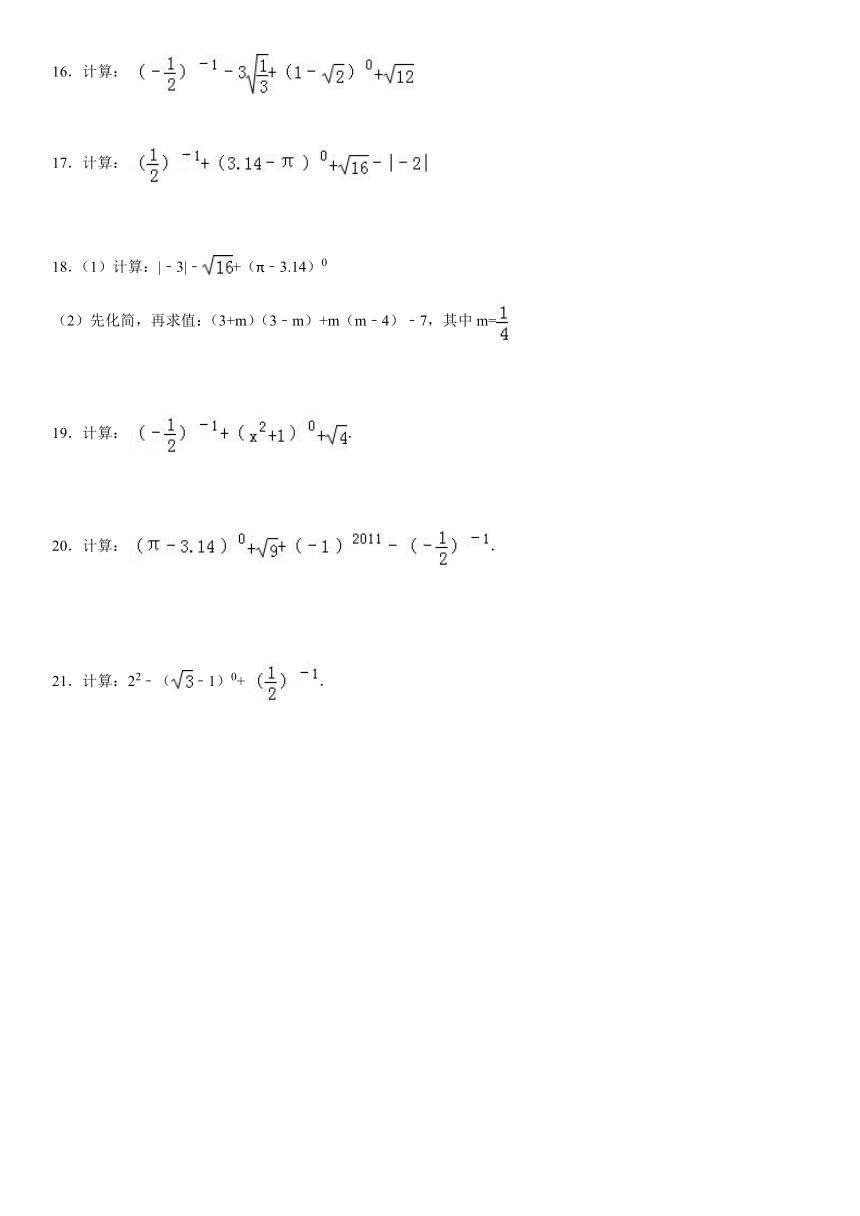


文档简介
16.4零指数与负整指数
农安县合隆中学 徐亚惠
一.选择题(共8小题)
1.一个代数式的值不能等于零,那么它是( )
A.a2 B.a0 C. D.|a|
2.π0的值是( )
A.π B.0 C.1 D.3.14
3.下列说法正确的是( )
A.a0=1 B.夹在两条平行线间的线段相等 C.勾股定理是a2+b2=c2 D.若有意义,则x≥1且x≠2
4.下列计算中,正确的是( )
A.a3 a2=a6 B.(π﹣3.14)0=1 C.()﹣1=﹣3 D.=±3
5.下列计算正确的是( )
A.(﹣1)﹣1=1 B.(﹣1)0=0 C.|﹣1|=﹣1 D.﹣(﹣1)2=﹣1
6.下列运算的结果中,是正数的是( )
A.(﹣2014)﹣1 B.﹣(2014)﹣1 C.(﹣1)×(﹣2014) D.(﹣2014)÷2014
7.2﹣1等于( )
A.2 B.﹣2 C. D.﹣
8.计算|﹣2|+(﹣1)0的结果是( )
A.1 B.2 C.3 D.﹣3
二.填空题(共6小题)
9.计算:= _________ .
10.若实数m,n 满足|m﹣2|+(n﹣2014)2=0,则m﹣1+n0= _________ .
11.2﹣2= _________ .
12.(﹣2014)0的平方根等于 _________ .
13.计算(﹣)0的结果等于 _________ .
14.3﹣1= _________ .
三.解答题(共8小题)
15.计算:.
16.计算:
17.计算:
18.(1)计算:|﹣3|﹣+(π﹣3.14)0
(2)先化简,再求值:(3+m)(3﹣m)+m(m﹣4)﹣7,其中m=
19.计算:.
20.计算:.
21.计算:22﹣(﹣1)0+.
16.4零指数与负整指数
参考答案与试题解析
一.选择题(共8小题)
1.一个代数式的值不能等于零,那么它是( )
A. a2 B.a0 C. D. |a|
考点: 零指数幂;绝对值;有理数的乘方;算术平方根.
分析: 根据非0的0次幂等于1,可得答案.
解答: 解:A、当a=0时,a2=0,故A错误;
B、a0=1(且a≠0),故B正确;
C、当a=0时,=0,故C错误;
D、当a=0时,|a|=0,故D错误.
故选:B.
点评: 本题考查了零指数幂,非0的0次幂等于1是解题关键.
2.π0的值是( )
A. π B.0 C.1 D. 3.14
考点: 零指数幂.
分析: 根据零指数幂的运算法则计算即可.
解答: 解:π0=1,
故选:C.
点评: 本题主要考查了零指数幂的运算.任何非0数的0次幂等于1.
3.下列说法正确的是( )
A. a0=1 B. 夹在两条平行线间的线段相等
C. 勾股定理是a2+b2=c2 D . 若有意义,则x≥1且x≠2
考点: 零指数幂;分式有意义的条件;二次根式有意义的条件;平行线之间的距离;勾股定理.
分析: 分别利用零指数幂的性质以及二次根式有意义的条件和勾股定理以及平行线的距离等知识,分别判断得出即可.
解答: 解:A、a0=1(a≠0),故A选项错误;
B、夹在两条平行线间的线段不一定相等,故B选项错误;
C、当∠C=90°,则由勾股定理得a2+b2=c2,故C选项错误;
D、若有意义,则x≥1且x≠2,此D选项正确.
故选:D.
点评: 此题主要考查了零指数幂的性质以及二次根式有意义的条件和勾股定理等知识,正确把握相关定义是解题关键.
4.下列计算中,正确的是( )
A. a3 a2=a6 B.(π﹣3.14)0=1 C.()﹣1=﹣3 D. =±3
考点: 负整数指数幂;算术平方根;同底数幂的乘法;零指数幂.
专题: 计算题.
分析: 根据同底数幂相乘,底数不变指数相加 ( http: / / www.21cnjy.com );任何非零数的零次幂等于1,负整数指数次幂等于正整数指数次幂的倒数,算术平方根的定义对各选项分析判断利用排除法求解.
解答: 解:A、a3 a2=a3+2=a5,故A选项错误;
B、(π﹣3.14)0=1,故B选项正确;
C、()﹣1=3,故C选项错误;
D、=3,故D选项错误.
故选:B.
点评: 本题考查了负整数指数次幂等于正整数指数次幂的倒数,同底数幂的乘法,零指数幂的定义以及算术平方根的定义,是基础题.
5.下列计算正确的是( )
A. (﹣1)﹣1=1 B. (﹣1)0=0 C. |﹣1|=﹣1 D. ﹣(﹣1)2=﹣1
考点: 负整数指数幂;绝对值;有理数的乘方;零指数幂.
专题: 计算题.
分析: 根据负整指数幂,可判断A,根据非0的0次幂,可判断B,根据负数的绝对值是正数,可判断C,根据相反数,可判断D.
解答: 解:A、(﹣1)﹣1=﹣1,故A错误;
B、(﹣1)0=1,故B错误;
C、|﹣1|=1,故C错误;
D、﹣(﹣1)2=﹣1,故D正确;
故选:D.
点评: 本题考查了负整指数幂,负整数指数为正整数指数的倒数;任何非0数的0次幂等于1.
6.下列运算的结果中,是正数的是( )
A. (﹣2014)﹣1 B. ﹣(2014)﹣1 C. (﹣1)×(﹣2014) D. (﹣2014)÷2014
考点: 负整数指数幂;正数和负数;有理数的乘法;有理数的除法.
分析: 分别根据负指数幂和有理数的乘除法进行计算求得结果,再判断正负即可.
解答: 解:A、原式=<0,故A错误;
B、原式=﹣<0,故B错误;
C、原式=1×2014=2014>0,故C正确;
D、原式=﹣2014÷2014=﹣1<0,故D错误;
故选:C.
点评: 本题主要考查了有理数的乘除法,负指数幂的运算.负整数指数为正整数指数的倒数.
7.2﹣1等于( )
A. 2 B. ﹣2 C. D. ﹣
考点: 负整数指数幂.
分析: 根据a,可得答案.
解答: 解:2,
故选:C.
点评: 本题考查了负整指数幂,负整数指数为正整数指数的倒数.
8.计算|﹣2|+(﹣1)0的结果是( )
A. 1 B. 2 C. 3 D. ﹣3
考点: 零指数幂;绝对值.
专题: 计算题.
分析: 根据绝对值的性质以及零指数幂的性质化简求出即可.
解答: 解:|﹣2|+(﹣1)0=2+1=3.
故选:C.
点评: 此题主要考查了绝对值的性质以及零指数幂的性质,正确化简各式是解题关键.
二.填空题(共6小题)
9.计算:= 9 .
考点: 负整数指数幂.
专题: 计算题.
分析: 根据负整数指数幂的运算法则进行计算即可.
解答: 解:原式===9.
故答案为:9.
点评: 本题考查的是负整数指数幂,即负整数指数幂等于该数对应的正整数指数幂的倒数.
10.若实数m,n 满足|m﹣2|+(n﹣2014)2=0,则m﹣1+n0= .
考点: 负整数指数幂;非负数的性质:绝对值;非负数的性质:偶次方;零指数幂.
分析: 根据绝对值与平方的和为0,可得绝对值与平方同时为0,根据负整指数幂、非0的0次幂,可得答案.
解答: 解:|m﹣2|+(n﹣2014)2=0,
m﹣2=0,n﹣2014=0,
m=2,n=2014.
m﹣1+n0=2﹣1+20140=+1=,
故答案为:.
点评: 本题考查了负整指数幂,先求出m、n的值,再求出负整指数幂、0次幂.
11.2﹣2= .
考点: 负整数指数幂.
分析: 根据负整数指数幂的运算法则直接进行计算即可.
解答: 解:2﹣2==.
故答案为:.
点评: 本题主要考查负整数指数幂,幂的负整数指数运算,先把底数化成其倒数,然后将负整数指数幂当成正的进行计算.
12.(﹣2014)0的平方根等于 ±1 .
考点: 零指数幂.
分析: 根据零指数幂:a0=1(a≠0)可得(﹣2014)0=1,再根据平方根可得答案.
解答: 解:(﹣2014)0=1,
1的平方根为±1,
故答案为:±1.
点评: 本题主要考查了零指数幂的运算,以及平方根.关键是掌握任何非0数的0次幂等于1.
13.计算(﹣)0的结果等于 1 .
考点: 零指数幂.
分析: 根据零指数幂:a0=1(a≠0)可得答案.
解答: 解:(﹣)0=1,
故答案为:1.
点评: 此题主要考查了零指数幂,关键是掌握计算公式.
14.3﹣1= .
考点: 负整数指数幂.
专题: 常规题型.
分析: 根据有理数的负整数次幂等于正整数次幂的倒数进行计算即可.
解答: 解:3﹣1=.
故答案为:.
点评: 本题主要考查了有理数的负整数指数次幂等于正整数次幂的倒数的性质,熟记性质是解题的关键.
三.解答题(共8小题)
15.计算:.
考点: 负整数指数幂;绝对值;有理数的乘方;零指数幂.
专题: 计算题.
分析: 本题涉及零指数幂、负整数指数幂、平方、绝对值.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答: 解:原式=3﹣1+4=6.故答案为6.
点评: 本题考查实数的运算能力,解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、绝对值等考点的运算.注意:负指数为正指数的倒数;任何非0数的0次幂等于1;利用绝对值的性质化简.
16.计算:
考点: 负整数指数幂;零指数幂.
专题: 计算题.
分析: 分别根据二次根式的化简、零指数幂,负指数幂的运算法则计算,然后根据实数的运算法则求得计算结果.
解答: 解:原式=﹣2﹣+1+2
=﹣1.
点评: 本题主要考查了二次根式的化简、零指数幂,负指数幂的运算.负整数指数为正整数指数的倒数;任何非0数的0次幂等于1.
17.计算:
考点: 负整数指数幂;零指数幂.
专题: 计算题.
分析: 分别根据零指数幂、负指数幂的运算法则,以及开方和绝对值的性质计算,然后根据实数的运算法则求得计算结果.
解答: 解:,
=2+1+4﹣2,
=5.
故答案为:5.
点评: 本题主要考查了零指数幂、负指数幂的运算法则以及开方和绝对值的性质.负整数指数为正整数指数的倒数;任何非0数的0次幂等于1.
18.(1)计算:|﹣3|﹣+(π﹣3.14)0
(2)先化简,再求值:(3+m)(3﹣m)+m(m﹣4)﹣7,其中m=
考点: 零指数幂;算术平方根;实数的运算;整式的混合运算—化简求值.
专题: 计算题.
分析: (1)本题涉及零指数幂、绝对值、算术平方根3个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;
(2)先化简,利用乘法公式,单项式乘以多项式的乘法运算法则进行,再代值计算.
解答: 解:(1)原式=3﹣4+1
=0;
(2)原式=9﹣m2+m2﹣4m﹣7
=2﹣4m,
当m=时,原式=2﹣4×=1.
点评: 实数的运算,要熟练掌握算术平方根、零指数幂、绝对值等考点的运算;化简求值题,先根据整式的运算法则把代数式化简,再求值.
19.计算:.
考点: 零指数幂;算术平方根;负整数指数幂.
专题: 计算题.
分析: 分别根据零指数幂、算术平方根、负指数幂的运算法则计算,然后根据实数的运算法则求得计算结果.
解答: 解:原式=(﹣2)+1+2=1,故答案为1.
点评: 本题主要考查了零指数幂,负指数幂的运算以及算术平方根.负整数指数为正整数指数的倒数;任何非0数的0次幂等于1.
20.计算:.
考点: 负整数指数幂;零指数幂.
专题: 计算题.
分析: 分别根据零指数幂,负指数幂的运算法则计算,然后根据实数的运算法则求得计算结果.
解答: 解:
=1+3﹣1﹣(﹣2)
=5.
故答案为5.
点评: 本题主要考查了零指数幂,负指数幂的运算.负整数指数为正整数指数的倒数;任何非0数的0次幂等于1.
21.计算:22﹣(﹣1)0+.
考点: 负整数指数幂;有理数的乘方;零指数幂.
分析: 根据零指数幂和负整数指数幂的知识进行解答,任何不等于0的数的0次幂都等于1,==2.
解答: 解:原式=4﹣1+2=5.
点评: 掌握0次幂的性质和负指数的转换方法.
农安县合隆中学 徐亚惠
一.选择题(共8小题)
1.一个代数式的值不能等于零,那么它是( )
A.a2 B.a0 C. D.|a|
2.π0的值是( )
A.π B.0 C.1 D.3.14
3.下列说法正确的是( )
A.a0=1 B.夹在两条平行线间的线段相等 C.勾股定理是a2+b2=c2 D.若有意义,则x≥1且x≠2
4.下列计算中,正确的是( )
A.a3 a2=a6 B.(π﹣3.14)0=1 C.()﹣1=﹣3 D.=±3
5.下列计算正确的是( )
A.(﹣1)﹣1=1 B.(﹣1)0=0 C.|﹣1|=﹣1 D.﹣(﹣1)2=﹣1
6.下列运算的结果中,是正数的是( )
A.(﹣2014)﹣1 B.﹣(2014)﹣1 C.(﹣1)×(﹣2014) D.(﹣2014)÷2014
7.2﹣1等于( )
A.2 B.﹣2 C. D.﹣
8.计算|﹣2|+(﹣1)0的结果是( )
A.1 B.2 C.3 D.﹣3
二.填空题(共6小题)
9.计算:= _________ .
10.若实数m,n 满足|m﹣2|+(n﹣2014)2=0,则m﹣1+n0= _________ .
11.2﹣2= _________ .
12.(﹣2014)0的平方根等于 _________ .
13.计算(﹣)0的结果等于 _________ .
14.3﹣1= _________ .
三.解答题(共8小题)
15.计算:.
16.计算:
17.计算:
18.(1)计算:|﹣3|﹣+(π﹣3.14)0
(2)先化简,再求值:(3+m)(3﹣m)+m(m﹣4)﹣7,其中m=
19.计算:.
20.计算:.
21.计算:22﹣(﹣1)0+.
16.4零指数与负整指数
参考答案与试题解析
一.选择题(共8小题)
1.一个代数式的值不能等于零,那么它是( )
A. a2 B.a0 C. D. |a|
考点: 零指数幂;绝对值;有理数的乘方;算术平方根.
分析: 根据非0的0次幂等于1,可得答案.
解答: 解:A、当a=0时,a2=0,故A错误;
B、a0=1(且a≠0),故B正确;
C、当a=0时,=0,故C错误;
D、当a=0时,|a|=0,故D错误.
故选:B.
点评: 本题考查了零指数幂,非0的0次幂等于1是解题关键.
2.π0的值是( )
A. π B.0 C.1 D. 3.14
考点: 零指数幂.
分析: 根据零指数幂的运算法则计算即可.
解答: 解:π0=1,
故选:C.
点评: 本题主要考查了零指数幂的运算.任何非0数的0次幂等于1.
3.下列说法正确的是( )
A. a0=1 B. 夹在两条平行线间的线段相等
C. 勾股定理是a2+b2=c2 D . 若有意义,则x≥1且x≠2
考点: 零指数幂;分式有意义的条件;二次根式有意义的条件;平行线之间的距离;勾股定理.
分析: 分别利用零指数幂的性质以及二次根式有意义的条件和勾股定理以及平行线的距离等知识,分别判断得出即可.
解答: 解:A、a0=1(a≠0),故A选项错误;
B、夹在两条平行线间的线段不一定相等,故B选项错误;
C、当∠C=90°,则由勾股定理得a2+b2=c2,故C选项错误;
D、若有意义,则x≥1且x≠2,此D选项正确.
故选:D.
点评: 此题主要考查了零指数幂的性质以及二次根式有意义的条件和勾股定理等知识,正确把握相关定义是解题关键.
4.下列计算中,正确的是( )
A. a3 a2=a6 B.(π﹣3.14)0=1 C.()﹣1=﹣3 D. =±3
考点: 负整数指数幂;算术平方根;同底数幂的乘法;零指数幂.
专题: 计算题.
分析: 根据同底数幂相乘,底数不变指数相加 ( http: / / www.21cnjy.com );任何非零数的零次幂等于1,负整数指数次幂等于正整数指数次幂的倒数,算术平方根的定义对各选项分析判断利用排除法求解.
解答: 解:A、a3 a2=a3+2=a5,故A选项错误;
B、(π﹣3.14)0=1,故B选项正确;
C、()﹣1=3,故C选项错误;
D、=3,故D选项错误.
故选:B.
点评: 本题考查了负整数指数次幂等于正整数指数次幂的倒数,同底数幂的乘法,零指数幂的定义以及算术平方根的定义,是基础题.
5.下列计算正确的是( )
A. (﹣1)﹣1=1 B. (﹣1)0=0 C. |﹣1|=﹣1 D. ﹣(﹣1)2=﹣1
考点: 负整数指数幂;绝对值;有理数的乘方;零指数幂.
专题: 计算题.
分析: 根据负整指数幂,可判断A,根据非0的0次幂,可判断B,根据负数的绝对值是正数,可判断C,根据相反数,可判断D.
解答: 解:A、(﹣1)﹣1=﹣1,故A错误;
B、(﹣1)0=1,故B错误;
C、|﹣1|=1,故C错误;
D、﹣(﹣1)2=﹣1,故D正确;
故选:D.
点评: 本题考查了负整指数幂,负整数指数为正整数指数的倒数;任何非0数的0次幂等于1.
6.下列运算的结果中,是正数的是( )
A. (﹣2014)﹣1 B. ﹣(2014)﹣1 C. (﹣1)×(﹣2014) D. (﹣2014)÷2014
考点: 负整数指数幂;正数和负数;有理数的乘法;有理数的除法.
分析: 分别根据负指数幂和有理数的乘除法进行计算求得结果,再判断正负即可.
解答: 解:A、原式=<0,故A错误;
B、原式=﹣<0,故B错误;
C、原式=1×2014=2014>0,故C正确;
D、原式=﹣2014÷2014=﹣1<0,故D错误;
故选:C.
点评: 本题主要考查了有理数的乘除法,负指数幂的运算.负整数指数为正整数指数的倒数.
7.2﹣1等于( )
A. 2 B. ﹣2 C. D. ﹣
考点: 负整数指数幂.
分析: 根据a,可得答案.
解答: 解:2,
故选:C.
点评: 本题考查了负整指数幂,负整数指数为正整数指数的倒数.
8.计算|﹣2|+(﹣1)0的结果是( )
A. 1 B. 2 C. 3 D. ﹣3
考点: 零指数幂;绝对值.
专题: 计算题.
分析: 根据绝对值的性质以及零指数幂的性质化简求出即可.
解答: 解:|﹣2|+(﹣1)0=2+1=3.
故选:C.
点评: 此题主要考查了绝对值的性质以及零指数幂的性质,正确化简各式是解题关键.
二.填空题(共6小题)
9.计算:= 9 .
考点: 负整数指数幂.
专题: 计算题.
分析: 根据负整数指数幂的运算法则进行计算即可.
解答: 解:原式===9.
故答案为:9.
点评: 本题考查的是负整数指数幂,即负整数指数幂等于该数对应的正整数指数幂的倒数.
10.若实数m,n 满足|m﹣2|+(n﹣2014)2=0,则m﹣1+n0= .
考点: 负整数指数幂;非负数的性质:绝对值;非负数的性质:偶次方;零指数幂.
分析: 根据绝对值与平方的和为0,可得绝对值与平方同时为0,根据负整指数幂、非0的0次幂,可得答案.
解答: 解:|m﹣2|+(n﹣2014)2=0,
m﹣2=0,n﹣2014=0,
m=2,n=2014.
m﹣1+n0=2﹣1+20140=+1=,
故答案为:.
点评: 本题考查了负整指数幂,先求出m、n的值,再求出负整指数幂、0次幂.
11.2﹣2= .
考点: 负整数指数幂.
分析: 根据负整数指数幂的运算法则直接进行计算即可.
解答: 解:2﹣2==.
故答案为:.
点评: 本题主要考查负整数指数幂,幂的负整数指数运算,先把底数化成其倒数,然后将负整数指数幂当成正的进行计算.
12.(﹣2014)0的平方根等于 ±1 .
考点: 零指数幂.
分析: 根据零指数幂:a0=1(a≠0)可得(﹣2014)0=1,再根据平方根可得答案.
解答: 解:(﹣2014)0=1,
1的平方根为±1,
故答案为:±1.
点评: 本题主要考查了零指数幂的运算,以及平方根.关键是掌握任何非0数的0次幂等于1.
13.计算(﹣)0的结果等于 1 .
考点: 零指数幂.
分析: 根据零指数幂:a0=1(a≠0)可得答案.
解答: 解:(﹣)0=1,
故答案为:1.
点评: 此题主要考查了零指数幂,关键是掌握计算公式.
14.3﹣1= .
考点: 负整数指数幂.
专题: 常规题型.
分析: 根据有理数的负整数次幂等于正整数次幂的倒数进行计算即可.
解答: 解:3﹣1=.
故答案为:.
点评: 本题主要考查了有理数的负整数指数次幂等于正整数次幂的倒数的性质,熟记性质是解题的关键.
三.解答题(共8小题)
15.计算:.
考点: 负整数指数幂;绝对值;有理数的乘方;零指数幂.
专题: 计算题.
分析: 本题涉及零指数幂、负整数指数幂、平方、绝对值.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答: 解:原式=3﹣1+4=6.故答案为6.
点评: 本题考查实数的运算能力,解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、绝对值等考点的运算.注意:负指数为正指数的倒数;任何非0数的0次幂等于1;利用绝对值的性质化简.
16.计算:
考点: 负整数指数幂;零指数幂.
专题: 计算题.
分析: 分别根据二次根式的化简、零指数幂,负指数幂的运算法则计算,然后根据实数的运算法则求得计算结果.
解答: 解:原式=﹣2﹣+1+2
=﹣1.
点评: 本题主要考查了二次根式的化简、零指数幂,负指数幂的运算.负整数指数为正整数指数的倒数;任何非0数的0次幂等于1.
17.计算:
考点: 负整数指数幂;零指数幂.
专题: 计算题.
分析: 分别根据零指数幂、负指数幂的运算法则,以及开方和绝对值的性质计算,然后根据实数的运算法则求得计算结果.
解答: 解:,
=2+1+4﹣2,
=5.
故答案为:5.
点评: 本题主要考查了零指数幂、负指数幂的运算法则以及开方和绝对值的性质.负整数指数为正整数指数的倒数;任何非0数的0次幂等于1.
18.(1)计算:|﹣3|﹣+(π﹣3.14)0
(2)先化简,再求值:(3+m)(3﹣m)+m(m﹣4)﹣7,其中m=
考点: 零指数幂;算术平方根;实数的运算;整式的混合运算—化简求值.
专题: 计算题.
分析: (1)本题涉及零指数幂、绝对值、算术平方根3个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;
(2)先化简,利用乘法公式,单项式乘以多项式的乘法运算法则进行,再代值计算.
解答: 解:(1)原式=3﹣4+1
=0;
(2)原式=9﹣m2+m2﹣4m﹣7
=2﹣4m,
当m=时,原式=2﹣4×=1.
点评: 实数的运算,要熟练掌握算术平方根、零指数幂、绝对值等考点的运算;化简求值题,先根据整式的运算法则把代数式化简,再求值.
19.计算:.
考点: 零指数幂;算术平方根;负整数指数幂.
专题: 计算题.
分析: 分别根据零指数幂、算术平方根、负指数幂的运算法则计算,然后根据实数的运算法则求得计算结果.
解答: 解:原式=(﹣2)+1+2=1,故答案为1.
点评: 本题主要考查了零指数幂,负指数幂的运算以及算术平方根.负整数指数为正整数指数的倒数;任何非0数的0次幂等于1.
20.计算:.
考点: 负整数指数幂;零指数幂.
专题: 计算题.
分析: 分别根据零指数幂,负指数幂的运算法则计算,然后根据实数的运算法则求得计算结果.
解答: 解:
=1+3﹣1﹣(﹣2)
=5.
故答案为5.
点评: 本题主要考查了零指数幂,负指数幂的运算.负整数指数为正整数指数的倒数;任何非0数的0次幂等于1.
21.计算:22﹣(﹣1)0+.
考点: 负整数指数幂;有理数的乘方;零指数幂.
分析: 根据零指数幂和负整数指数幂的知识进行解答,任何不等于0的数的0次幂都等于1,==2.
解答: 解:原式=4﹣1+2=5.
点评: 掌握0次幂的性质和负指数的转换方法.
