4.7 相似三角形的性质(无答案)2023-2024学年北师大版数学九年级上册
文档属性
| 名称 | 4.7 相似三角形的性质(无答案)2023-2024学年北师大版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 366.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 14:13:27 | ||
图片预览

文档简介
北师大版九年级上册4.7 相似三角形的性质
一、选择题
1. 已知,,若,则( )
A.4 B.6 C.8 D.16
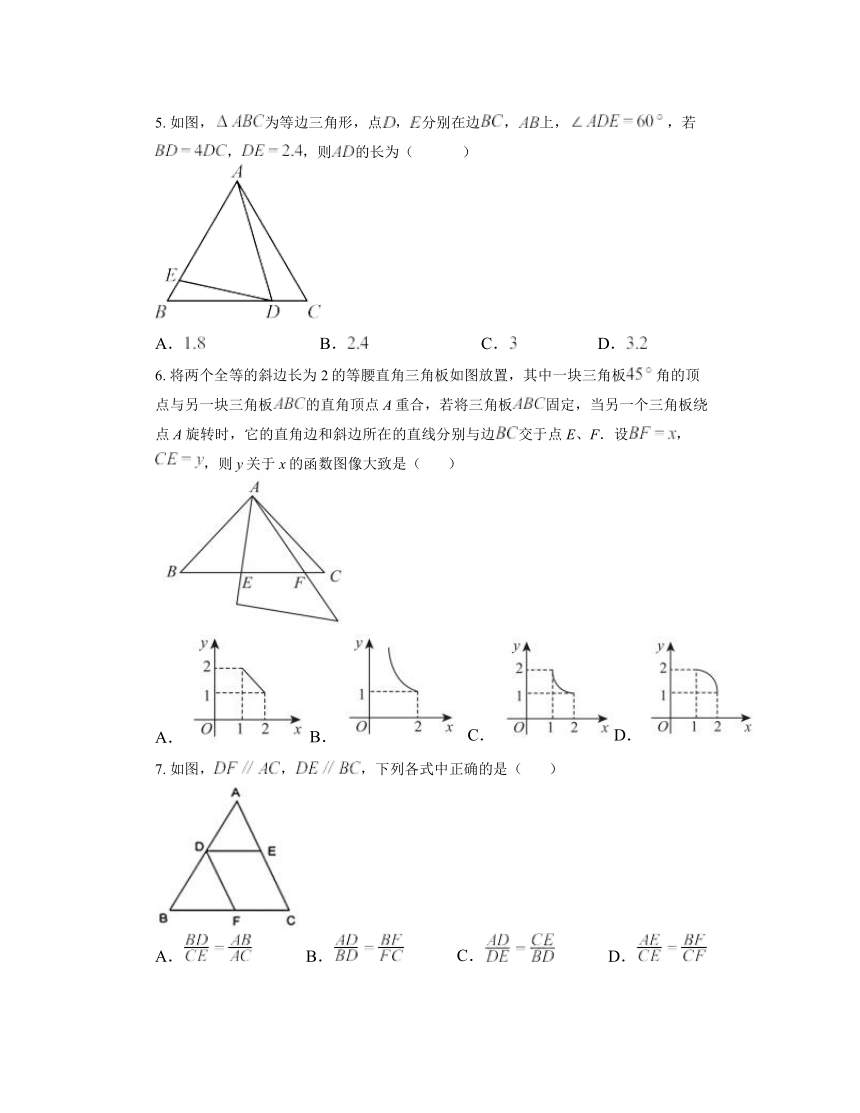
2. 如图,小明站在C处看甲、乙两楼楼顶上的点A和点 E.C,E,A三点在同一直线上,B,C相距20米,D,C相距40米,乙楼的高为15米,小明的身高忽略不计,则甲楼的高为( )
A.40米 B.20米 C.15米 D.30米
3. 如图,点,,,分别是四边形各边的中点,现随机向四边形内掷一枚小针,则针尖落在白色区域内的概率为( )
A. B. C. D.
4. 如图,E,F,G,H分别是矩形四条边上的点,已知,若,,则为( )
A. B. C. D.
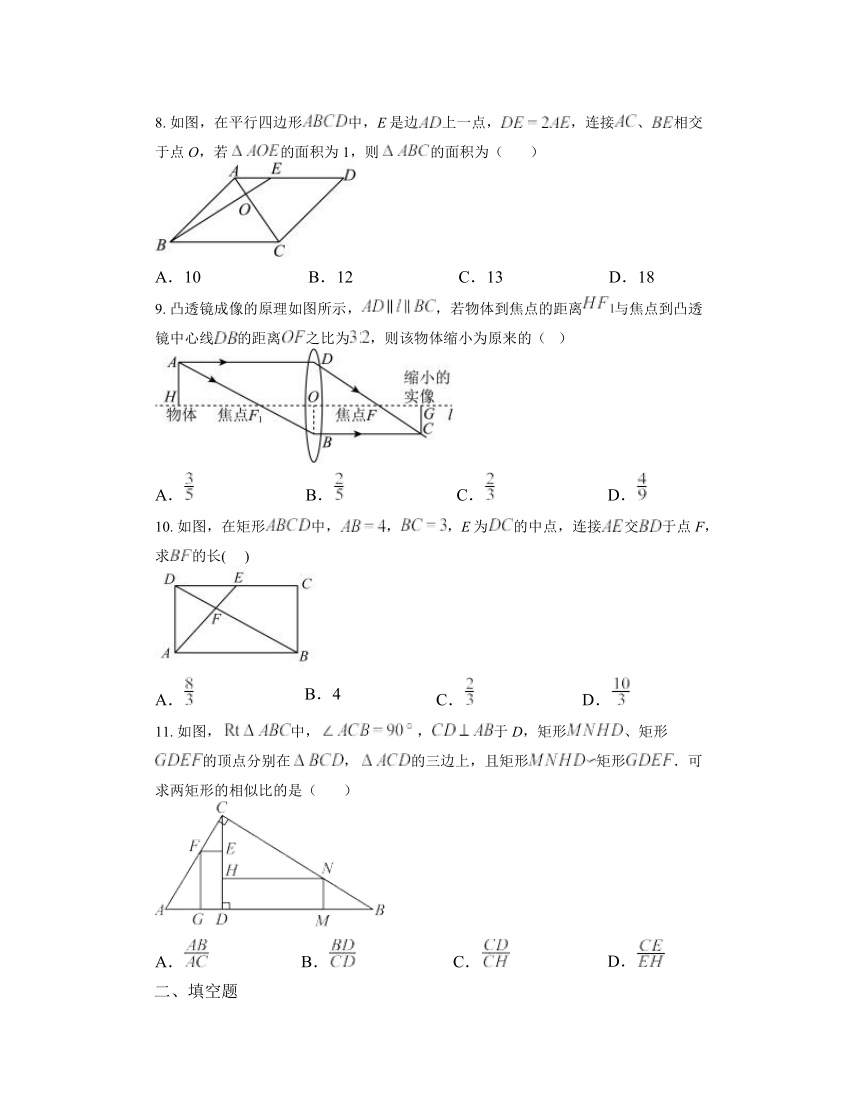
5. 如图,为等边三角形,点,分别在边,上,,若,,则的长为( )
A. B. C. D.
6. 将两个全等的斜边长为2的等腰直角三角板如图放置,其中一块三角板角的顶点与另一块三角板的直角顶点A重合,若将三角板固定,当另一个三角板绕点A旋转时,它的直角边和斜边所在的直线分别与边交于点E、F.设,,则y关于x的函数图像大致是( )
A. B. C. D.
7. 如图,,,下列各式中正确的是( )
A. B. C. D.
8. 如图,在平行四边形中,E是边上一点,,连接、相交于点O,若的面积为1,则的面积为( )
A.10 B.12 C.13 D.18
9. 凸透镜成像的原理如图所示,,若物体到焦点的距离与焦点到凸透镜中心线的距离之比为,则该物体缩小为原来的( )
A. B. C. D.
10. 如图,在矩形中,,,E为的中点,连接交于点F,求的长( )
A. B.4 C. D.
11. 如图, 中,,于D,矩形、矩形的顶点分别在,的三边上,且矩形矩形.可求两矩形的相似比的是( )
A. B. C. D.
二、填空题
12. 在阳光下,高为6m的旗杆在地面上的影长为4m,在同一时刻,测得附近一座建筑物的影长为,则这座建筑物的高度为_________m.
13. 如图,正方形的对角线、交于点O,E是的中点,连接,过点A作于点M,交于F,若,则______.
14. 如图,在矩形中,是边的中点,连接交对角线于点,若,,则的长为__________.
15. 如图,和都是等边三角形,点在上,交于点,若,,则的长是______.
三、解答题
16. 如图,在中,D为上一点,.求的长.
17. 党的二十大报告提出要“全面推进乡村振兴”,这是对党的十九大报告所提出的“实施乡村振兴战略”的进一步发展,彰显出新时代新征程在工农城乡关系布局上的深远谋划,为不断推进乡村振兴、加快农村现代化进程指明了方向某市为了加快城乡发展,保障市民出行方便,在流经该市的河流上架起一座桥,连通南北,铺就城市繁荣之路.小明和小颖想通过自己所学的数学知识计算该桥的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在的延长线上取点,使得.经测量,米,米,且点E到河岸的距离为60米.已知于点F,请你根据提供的数据,帮助他们计算桥的长度.
18. 如图,在中,,,将线段绕点逆时针旋转角得到线段,连接,过点作于点,连接,分别交、于点、.
(1)当时,求的大小;
(2)当时,试写出线段与满足的数量关系,并证明;
(3)若为线段的中点,求的长.
19. 如图,在正方形中,为上一点,连接,的垂直平分线交于点,交于点,垂足为,点在上,且.
(1)求证:;
(2)若,,求的长.
20. 同学们还记得吗?图①是我们研究过的湘教版八年级上册教材P99第16题“已知,如图在等腰三角形中,,是的中点,点、分别在、上求证:”的图形;图②是我们研究过的湘教版九年级上册教材第2题“如图,,,是的中点.已知,,求的长.”的图形,受这两个图形的启发,数学兴趣小组提出了以下三个问题,请你回答:
(1)【问题一】受图①启发,兴趣小组画出了图③,正方形的对角线相交于点,点又是正方形的一个顶点,交于点,交于点,则与的数量关系为_________;
(2)【问题二】受图①启发,兴趣小组画出了图④:直线、经过正方形的对称中心,直线分别与、交于点、,直线分别与、交于点、,且,若正方形边长为8,求四边形的面积;
(3)【问题三】受图②启发,兴趣小组画出了图⑤:正方形的顶点在正方形的边上,顶点在的延长线上,且,.在直线上是否存在点,使为直角三角形?若存在,求出的长度;若不存在,说明理由.
一、选择题
1. 已知,,若,则( )
A.4 B.6 C.8 D.16
2. 如图,小明站在C处看甲、乙两楼楼顶上的点A和点 E.C,E,A三点在同一直线上,B,C相距20米,D,C相距40米,乙楼的高为15米,小明的身高忽略不计,则甲楼的高为( )
A.40米 B.20米 C.15米 D.30米
3. 如图,点,,,分别是四边形各边的中点,现随机向四边形内掷一枚小针,则针尖落在白色区域内的概率为( )
A. B. C. D.
4. 如图,E,F,G,H分别是矩形四条边上的点,已知,若,,则为( )
A. B. C. D.
5. 如图,为等边三角形,点,分别在边,上,,若,,则的长为( )
A. B. C. D.
6. 将两个全等的斜边长为2的等腰直角三角板如图放置,其中一块三角板角的顶点与另一块三角板的直角顶点A重合,若将三角板固定,当另一个三角板绕点A旋转时,它的直角边和斜边所在的直线分别与边交于点E、F.设,,则y关于x的函数图像大致是( )
A. B. C. D.
7. 如图,,,下列各式中正确的是( )
A. B. C. D.
8. 如图,在平行四边形中,E是边上一点,,连接、相交于点O,若的面积为1,则的面积为( )
A.10 B.12 C.13 D.18
9. 凸透镜成像的原理如图所示,,若物体到焦点的距离与焦点到凸透镜中心线的距离之比为,则该物体缩小为原来的( )
A. B. C. D.
10. 如图,在矩形中,,,E为的中点,连接交于点F,求的长( )
A. B.4 C. D.
11. 如图, 中,,于D,矩形、矩形的顶点分别在,的三边上,且矩形矩形.可求两矩形的相似比的是( )
A. B. C. D.
二、填空题
12. 在阳光下,高为6m的旗杆在地面上的影长为4m,在同一时刻,测得附近一座建筑物的影长为,则这座建筑物的高度为_________m.
13. 如图,正方形的对角线、交于点O,E是的中点,连接,过点A作于点M,交于F,若,则______.
14. 如图,在矩形中,是边的中点,连接交对角线于点,若,,则的长为__________.
15. 如图,和都是等边三角形,点在上,交于点,若,,则的长是______.
三、解答题
16. 如图,在中,D为上一点,.求的长.
17. 党的二十大报告提出要“全面推进乡村振兴”,这是对党的十九大报告所提出的“实施乡村振兴战略”的进一步发展,彰显出新时代新征程在工农城乡关系布局上的深远谋划,为不断推进乡村振兴、加快农村现代化进程指明了方向某市为了加快城乡发展,保障市民出行方便,在流经该市的河流上架起一座桥,连通南北,铺就城市繁荣之路.小明和小颖想通过自己所学的数学知识计算该桥的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在的延长线上取点,使得.经测量,米,米,且点E到河岸的距离为60米.已知于点F,请你根据提供的数据,帮助他们计算桥的长度.
18. 如图,在中,,,将线段绕点逆时针旋转角得到线段,连接,过点作于点,连接,分别交、于点、.
(1)当时,求的大小;
(2)当时,试写出线段与满足的数量关系,并证明;
(3)若为线段的中点,求的长.
19. 如图,在正方形中,为上一点,连接,的垂直平分线交于点,交于点,垂足为,点在上,且.
(1)求证:;
(2)若,,求的长.
20. 同学们还记得吗?图①是我们研究过的湘教版八年级上册教材P99第16题“已知,如图在等腰三角形中,,是的中点,点、分别在、上求证:”的图形;图②是我们研究过的湘教版九年级上册教材第2题“如图,,,是的中点.已知,,求的长.”的图形,受这两个图形的启发,数学兴趣小组提出了以下三个问题,请你回答:
(1)【问题一】受图①启发,兴趣小组画出了图③,正方形的对角线相交于点,点又是正方形的一个顶点,交于点,交于点,则与的数量关系为_________;
(2)【问题二】受图①启发,兴趣小组画出了图④:直线、经过正方形的对称中心,直线分别与、交于点、,直线分别与、交于点、,且,若正方形边长为8,求四边形的面积;
(3)【问题三】受图②启发,兴趣小组画出了图⑤:正方形的顶点在正方形的边上,顶点在的延长线上,且,.在直线上是否存在点,使为直角三角形?若存在,求出的长度;若不存在,说明理由.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
