第四章《图形的相似》高频考点靶向专题集训(无答案) 北师大版数学九年级上册
文档属性
| 名称 | 第四章《图形的相似》高频考点靶向专题集训(无答案) 北师大版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 634.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 00:00:00 | ||
图片预览



文档简介
北师大版九年级上册数学《图形的相似》高频考点靶向专题集训
考点一:成比例线段
1. 已知,,则 .
2.我们把顶角为的等腰三角形称为“黄金三角形”,它的底与腰的比值为.如图,在△ABC中,,,平分交于点D,若,则的长为 .
3.已知a、b、c是△ABC的三边长,且,求:
(1)的值;
(2)若△ABC的周长为90,求△ABC的面积.
考点二:平行线分线段成比例
1. 如图,在△ABC中,点,,分别在边,,上,且,.若,则的值为 .
2.如图,直线,直线和被直线、、所截,,,,则的长为 .
3.如图,△ABC中,,,,,,求的长.
考点三:相似多边形
1.两个相似多边形的面积之比为,则它们的对应高之比为 。
2.某校有两块相似的多边形草坪,其相似比为,其中较大的一块草坪的周长是36米,则另一块草坪的周长是米 。
3.一个矩形的较短边长为2.
(1)如图1,若沿长边对折后得到的矩形与原矩形相似,求的长;
(2)如图2,已知矩形的另一边长为4,剪去一个矩形后,余下的矩形与原矩形相似,求矩形的面积.
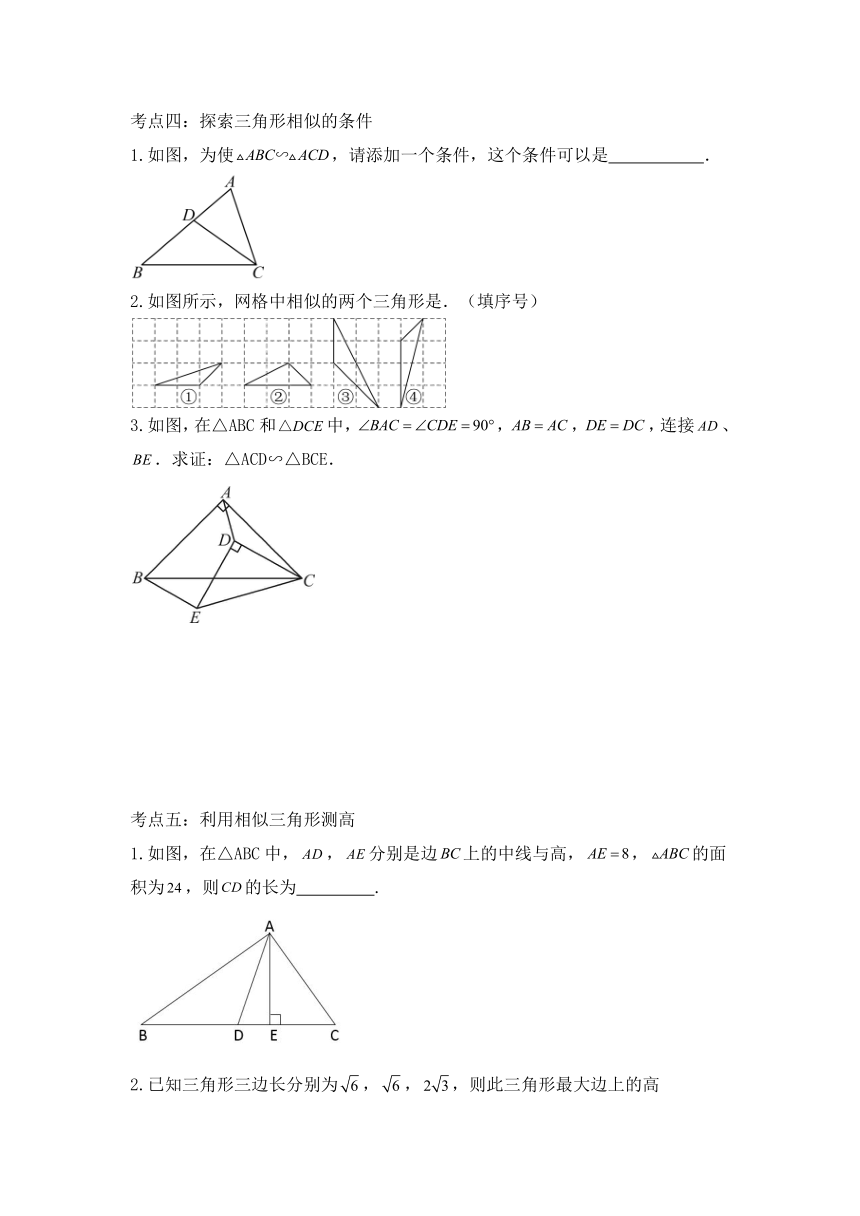
考点四:探索三角形相似的条件
1.如图,为使,请添加一个条件,这个条件可以是 .
2.如图所示,网格中相似的两个三角形是.(填序号)
3.如图,在△ABC和中,,,,连接、.求证:△ACD∽△BCE.
考点五:利用相似三角形测高
1.如图,在△ABC中,,分别是边上的中线与高,,的面积为,则的长为 .
2.已知三角形三边长分别为,,,则此三角形最大边上的高为 .
3.每年的秋冬季节,青竹湖湘一外国语学校的银杏大道是学校最为靓丽的一条风景线,数学彭老师有一天为了测量一棵高不可攀的银杏树高度,他利用了反射定律,利用一面镜子和皮尺,设计如图所示的测量方案:把镜子放在离银杏树m的点处,然后观测者沿着直线后退到点,这时恰好在镜子里看到树梢顶点,再用皮尺量得m,观测者目高m,则树高约是多少米?
考点六:相似三角形的性质
1.中,,三个正方形如图放置,边长分别为a,b,c,已知,,则c的值为 .
2.如图,△ABC是等边三角形,点、分别在、上,且,,,则的长等于 .
3. 如图,在平面直角坐标系中,直线:与x轴、y轴分别交于点A、点B,直线与x轴、y轴分别交于点C、点D,与相交于点E,且,.
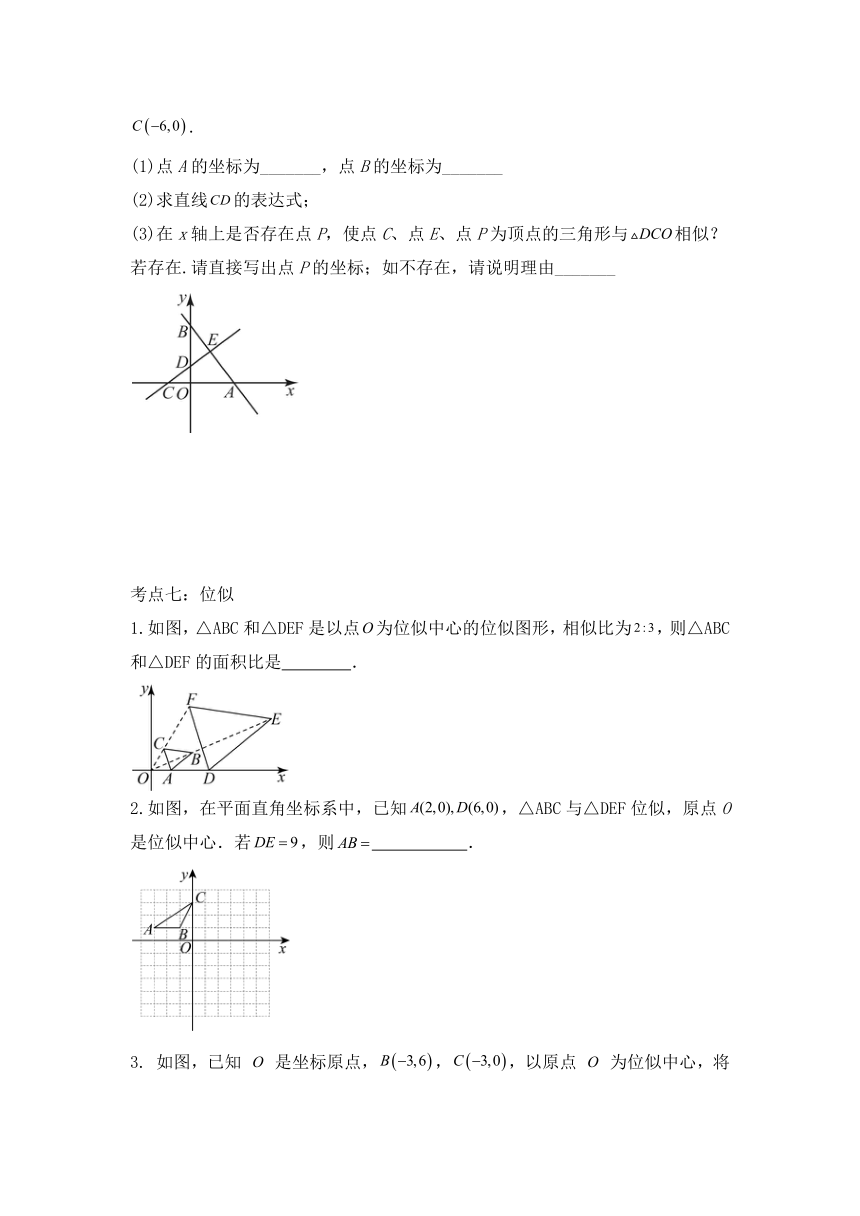
(1)点A的坐标为_______,点B的坐标为_______
(2)求直线的表达式;
(3)在x轴上是否存在点P,使点C、点E、点P为顶点的三角形与相似?若存在.请直接写出点P的坐标;如不存在,请说明理由_______
考点七:位似
1.如图,△ABC和△DEF是以点为位似中心的位似图形,相似比为,则△ABC和△DEF的面积比是 .
2.如图,在平面直角坐标系中,已知,△ABC与△DEF位似,原点O是位似中心.若,则 .
3. 如图,已知 是坐标原点,,,以原点 为位似中心,将 在其内部缩小为原来的一半(即新图形与原图形的相似比为 ).
(1)画出缩小后的图形;
(2)写出点的对应点坐标;
(3)如果 内部一点 的坐标为 ,写出点 经位似变换后的对应点坐标.
考点八:相似综合问题
1. 综合与实践课上,老师让同学们以“矩形与垂直”为主题开展数学活动.
(1)操作判断
如图1,正方形纸片,在边上任意取一点,连接,过点作于点,与边交于点.根据以上操作,请直接写出图1中线段与线段的关系.
(2)迁移探究
小华将正方形纸片换成矩形纸片,继续探究,过程如下:
如图2,在矩形纸片中,,在边上任意取一点,连接,过点作于点,与边交于点,请求出线段与的关系,并说明理由.
(3)拓展应用
如图3,已知正方形纸片的边长为2,动点由点向终点做匀速运动,动点由点向终点做匀速运动,动点、同时开始运动,且速度相同,连接、,交于点,连接,则线段长度的最小值为______,点的运动轨迹的长为______.(直接写出答案不必说明理由)
2.在中,,将绕点B顺时针旋转得到,其中点A,C的对应点分别为点,.
(1)如图1,当点落在的延长线上时,求的长;
(2)如图2,当点落在的延长线上时,连接,交于点M,求的长;
(3)如图3,连接,,直线交于点D,点E为的中点,连接.在旋转过程中,是否存在最小值?若存在,求出的最小值;若不存在,请说明理由.
3.如图:在如图1所示的平面直角坐标系中,直线交x轴于点A,交y轴于点B,点C与点A关于y轴对称.
(1)求直线的解析式;
(2)如图2,点E在线段上,点D在线段上,且,若点E的横坐标为t,三角形的面积为S,求S与t之间的函数关系式(不要求写出自变量的取值范围);
(3)如图3,在(2)问的条件下,点H是点B关于x轴的对称点,连接,过点B作的垂线,交于点G,交x轴于点F,交于点K,若,求点E的坐标.
考点一:成比例线段
1. 已知,,则 .
2.我们把顶角为的等腰三角形称为“黄金三角形”,它的底与腰的比值为.如图,在△ABC中,,,平分交于点D,若,则的长为 .
3.已知a、b、c是△ABC的三边长,且,求:
(1)的值;
(2)若△ABC的周长为90,求△ABC的面积.
考点二:平行线分线段成比例
1. 如图,在△ABC中,点,,分别在边,,上,且,.若,则的值为 .
2.如图,直线,直线和被直线、、所截,,,,则的长为 .
3.如图,△ABC中,,,,,,求的长.
考点三:相似多边形
1.两个相似多边形的面积之比为,则它们的对应高之比为 。
2.某校有两块相似的多边形草坪,其相似比为,其中较大的一块草坪的周长是36米,则另一块草坪的周长是米 。
3.一个矩形的较短边长为2.
(1)如图1,若沿长边对折后得到的矩形与原矩形相似,求的长;
(2)如图2,已知矩形的另一边长为4,剪去一个矩形后,余下的矩形与原矩形相似,求矩形的面积.
考点四:探索三角形相似的条件
1.如图,为使,请添加一个条件,这个条件可以是 .
2.如图所示,网格中相似的两个三角形是.(填序号)
3.如图,在△ABC和中,,,,连接、.求证:△ACD∽△BCE.
考点五:利用相似三角形测高
1.如图,在△ABC中,,分别是边上的中线与高,,的面积为,则的长为 .
2.已知三角形三边长分别为,,,则此三角形最大边上的高为 .
3.每年的秋冬季节,青竹湖湘一外国语学校的银杏大道是学校最为靓丽的一条风景线,数学彭老师有一天为了测量一棵高不可攀的银杏树高度,他利用了反射定律,利用一面镜子和皮尺,设计如图所示的测量方案:把镜子放在离银杏树m的点处,然后观测者沿着直线后退到点,这时恰好在镜子里看到树梢顶点,再用皮尺量得m,观测者目高m,则树高约是多少米?
考点六:相似三角形的性质
1.中,,三个正方形如图放置,边长分别为a,b,c,已知,,则c的值为 .
2.如图,△ABC是等边三角形,点、分别在、上,且,,,则的长等于 .
3. 如图,在平面直角坐标系中,直线:与x轴、y轴分别交于点A、点B,直线与x轴、y轴分别交于点C、点D,与相交于点E,且,.
(1)点A的坐标为_______,点B的坐标为_______
(2)求直线的表达式;
(3)在x轴上是否存在点P,使点C、点E、点P为顶点的三角形与相似?若存在.请直接写出点P的坐标;如不存在,请说明理由_______
考点七:位似
1.如图,△ABC和△DEF是以点为位似中心的位似图形,相似比为,则△ABC和△DEF的面积比是 .
2.如图,在平面直角坐标系中,已知,△ABC与△DEF位似,原点O是位似中心.若,则 .
3. 如图,已知 是坐标原点,,,以原点 为位似中心,将 在其内部缩小为原来的一半(即新图形与原图形的相似比为 ).
(1)画出缩小后的图形;
(2)写出点的对应点坐标;
(3)如果 内部一点 的坐标为 ,写出点 经位似变换后的对应点坐标.
考点八:相似综合问题
1. 综合与实践课上,老师让同学们以“矩形与垂直”为主题开展数学活动.
(1)操作判断
如图1,正方形纸片,在边上任意取一点,连接,过点作于点,与边交于点.根据以上操作,请直接写出图1中线段与线段的关系.
(2)迁移探究
小华将正方形纸片换成矩形纸片,继续探究,过程如下:
如图2,在矩形纸片中,,在边上任意取一点,连接,过点作于点,与边交于点,请求出线段与的关系,并说明理由.
(3)拓展应用
如图3,已知正方形纸片的边长为2,动点由点向终点做匀速运动,动点由点向终点做匀速运动,动点、同时开始运动,且速度相同,连接、,交于点,连接,则线段长度的最小值为______,点的运动轨迹的长为______.(直接写出答案不必说明理由)
2.在中,,将绕点B顺时针旋转得到,其中点A,C的对应点分别为点,.
(1)如图1,当点落在的延长线上时,求的长;
(2)如图2,当点落在的延长线上时,连接,交于点M,求的长;
(3)如图3,连接,,直线交于点D,点E为的中点,连接.在旋转过程中,是否存在最小值?若存在,求出的最小值;若不存在,请说明理由.
3.如图:在如图1所示的平面直角坐标系中,直线交x轴于点A,交y轴于点B,点C与点A关于y轴对称.
(1)求直线的解析式;
(2)如图2,点E在线段上,点D在线段上,且,若点E的横坐标为t,三角形的面积为S,求S与t之间的函数关系式(不要求写出自变量的取值范围);
(3)如图3,在(2)问的条件下,点H是点B关于x轴的对称点,连接,过点B作的垂线,交于点G,交x轴于点F,交于点K,若,求点E的坐标.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
