河北省保定市顺平县2023-2024学年八年级上学期月考数学试题(无答案)
文档属性
| 名称 | 河北省保定市顺平县2023-2024学年八年级上学期月考数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 517.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 14:51:06 | ||
图片预览

文档简介
2023-2024学年八年级(上)第一次月考数学试卷
第Ⅰ卷(选择题)
一、选择题(本大题共16小题,共38分.1-6题每题3分,7-16题每题2分.在每小题列出的选项中,选出符合题目的一项.)
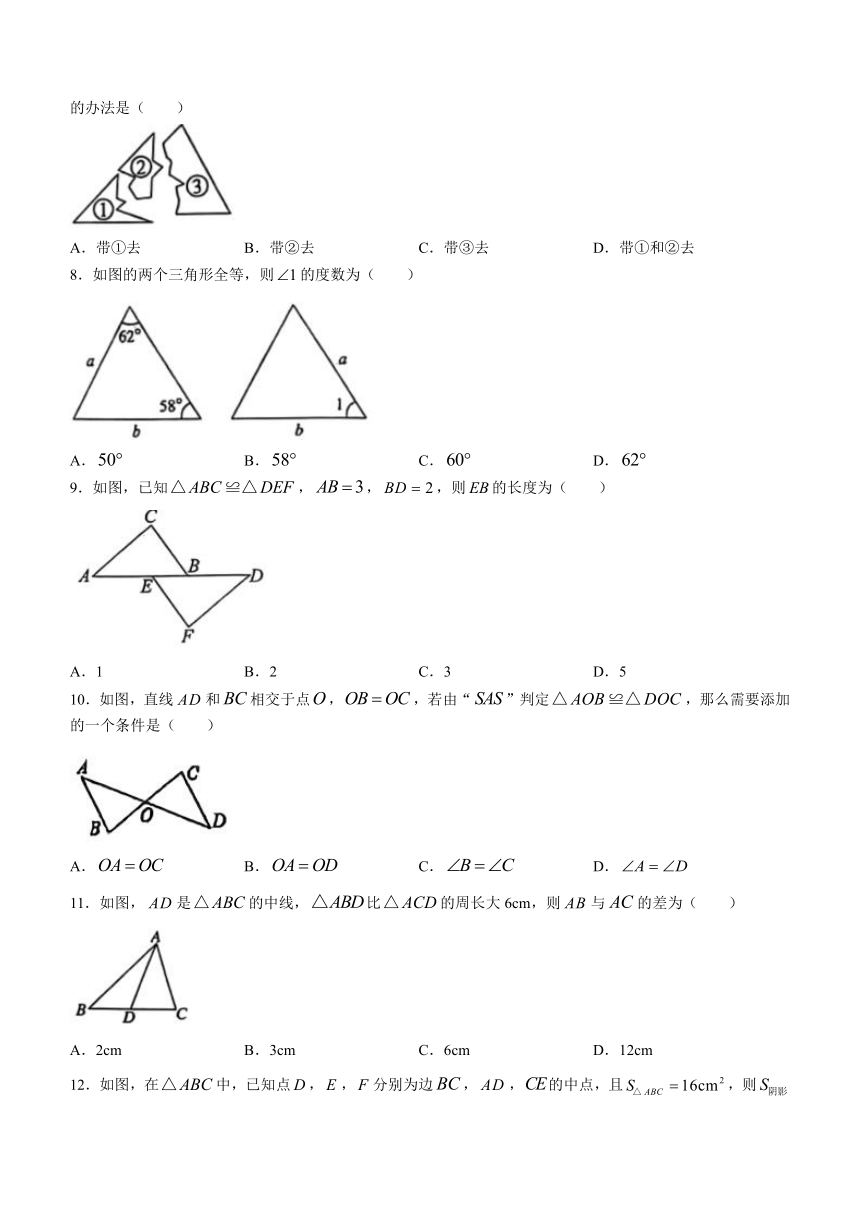
1.下列各组线段,能构成三角形的是( )
A.1cm,3cm,5cm B.2cm,4cm,6cm C.4cm,4cm,1cm D.8cm,8cm,20cm
2.一个缺角的三角形残片如图所示,量得,,则这个三角形残缺前的的度数为( )
A. B. C. D.
3.如图,小明做了一个长方形框架,发现很容易变形,请你帮他选择一个最好的加固方案( )
A. B. C. D.
4.下列四个图形中,线段是中边上的高的图形是( )
A. B.
C. D.
5.如图所示,,则( )
A. B. C. D.
6.将一个四边形截去一个角后,它不可能是( )
A.六边形 B.五边形 C.四边形 D.三角形
7.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A.带①去 B.带②去 C.带③去 D.带①和②去
8.如图的两个三角形全等,则的度数为( )
A. B. C. D.
9.如图,已知,,,则的长度为( )
A.1 B.2 C.3 D.5
10.如图,直线和相交于点,,若由“”判定,那么需要添加的一个条件是( )
A. B. C. D.
11.如图,是的中线,比的周长大6cm,则与的差为( )
A.2cm B.3cm C.6cm D.12cm
12.如图,在中,已知点,,分别为边,,的中点,且,则等于( )
A. B. C. D.
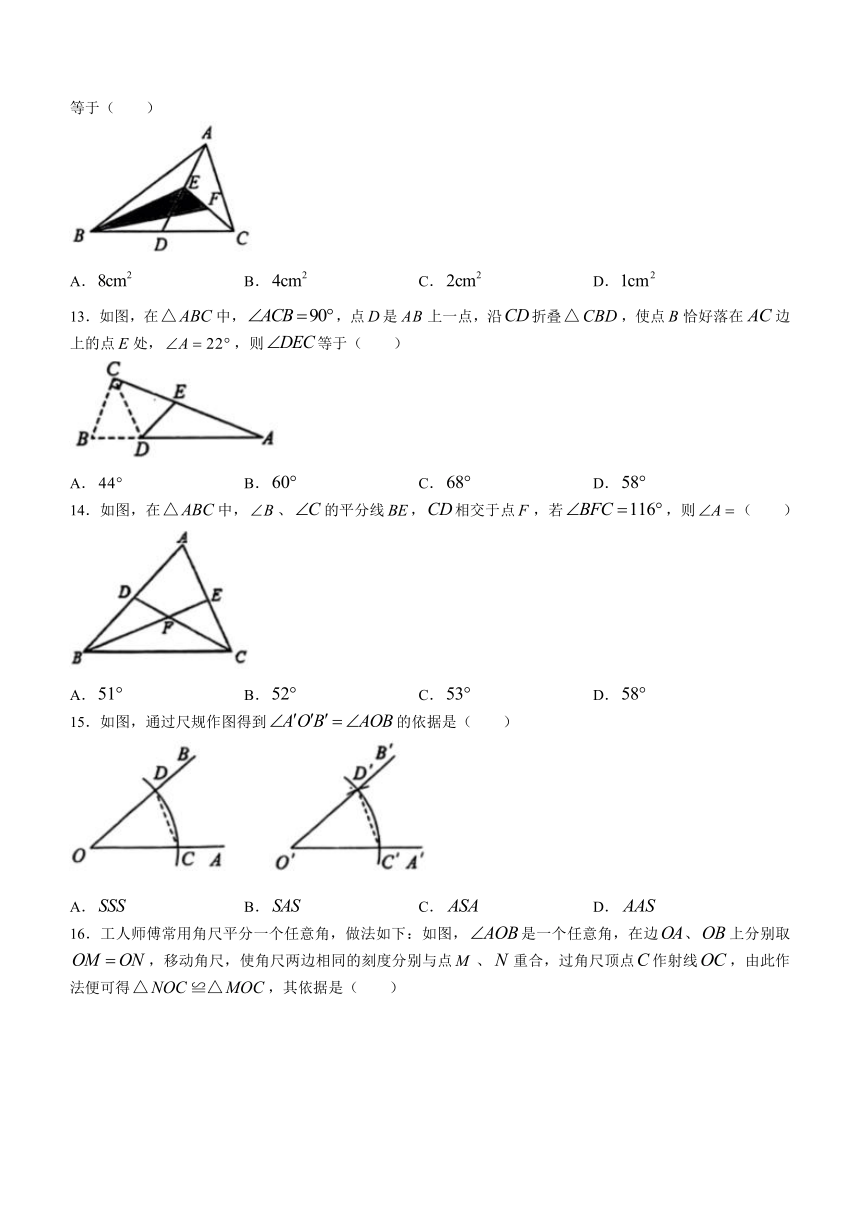
13.如图,在中,,点是上一点,沿折叠,使点恰好落在边上的点处,,则等于( )
A. B. C. D.
14.如图,在中,、的平分线,相交于点,若,则( )
A. B. C. D.
15.如图,通过尺规作图得到的依据是( )
A. B. C. D.
16.工人师傅常用角尺平分一个任意角,做法如下:如图,是一个任意角,在边、上分别取,移动角尺,使角尺两边相同的刻度分别与点、重合,过角尺顶点作射线,由此作法便可得,其依据是( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共3小题,共10分.17小题2分,18-19小题个4分,每空2分.)
17.三角形的两边长分别是10和8,则第三边的取值范围是________.
18.一个多边形的内角和是它外角和的3倍,则这个多边形是________边形,内角和是________度。
19.(1)如图,三角形纸片,,,,沿过点的直线折叠这个三角形,使顶点落在边上的点处,折痕为,则的周长为________cm.
(2)如图,点、、、在一条直线上,已知,,请你添加一个适当的条件________使得.
三、解答题(本题共7小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
20.(本小题9.0分)如果一个三角形的一边长为9cm、另一边长为1cm,求:
(1)这个三角形的第三边的范围;
(2)当第三边长为奇数时,求三角形的周长.
21.(本小题9.0分)如图,已知在四边形中,,.
(1)的度数为________;
(2)若的平分线交边于点,且,求的度数.
22.(本小题9.0分)如图,,,,求的度数.
23.(本小题10.0分)已知:如图,,,求证.
24.(本小题10.0分)如图,已知,点在上,与交于点,,,,
(1)求的长度;
(2)求的度数.
25.(本小题12.0分)如图,点,,,在同一条直线上,,相较于点,,,,求证:.
26.(本小题13.0分)(1)如图1,在中,,,是过点的一条直线,且,在的异侧,于点,于点,求证:.
图1
(2)若直线绕点旋转到图2的位置,其余条件不变,则与,之间的数量关系如何?请证明.
图2
(3)若直线绕点旋转到图3的位置,其余条件不变,则与,之间的数量关系如何?请直接写出结果,不需证明.
图3
(4)归纳(1)(2)(3),请用简洁的语言表述与,之间的数量关系.
第Ⅰ卷(选择题)
一、选择题(本大题共16小题,共38分.1-6题每题3分,7-16题每题2分.在每小题列出的选项中,选出符合题目的一项.)
1.下列各组线段,能构成三角形的是( )
A.1cm,3cm,5cm B.2cm,4cm,6cm C.4cm,4cm,1cm D.8cm,8cm,20cm
2.一个缺角的三角形残片如图所示,量得,,则这个三角形残缺前的的度数为( )
A. B. C. D.
3.如图,小明做了一个长方形框架,发现很容易变形,请你帮他选择一个最好的加固方案( )
A. B. C. D.
4.下列四个图形中,线段是中边上的高的图形是( )
A. B.
C. D.
5.如图所示,,则( )
A. B. C. D.
6.将一个四边形截去一个角后,它不可能是( )
A.六边形 B.五边形 C.四边形 D.三角形
7.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A.带①去 B.带②去 C.带③去 D.带①和②去
8.如图的两个三角形全等,则的度数为( )
A. B. C. D.
9.如图,已知,,,则的长度为( )
A.1 B.2 C.3 D.5
10.如图,直线和相交于点,,若由“”判定,那么需要添加的一个条件是( )
A. B. C. D.
11.如图,是的中线,比的周长大6cm,则与的差为( )
A.2cm B.3cm C.6cm D.12cm
12.如图,在中,已知点,,分别为边,,的中点,且,则等于( )
A. B. C. D.
13.如图,在中,,点是上一点,沿折叠,使点恰好落在边上的点处,,则等于( )
A. B. C. D.
14.如图,在中,、的平分线,相交于点,若,则( )
A. B. C. D.
15.如图,通过尺规作图得到的依据是( )
A. B. C. D.
16.工人师傅常用角尺平分一个任意角,做法如下:如图,是一个任意角,在边、上分别取,移动角尺,使角尺两边相同的刻度分别与点、重合,过角尺顶点作射线,由此作法便可得,其依据是( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共3小题,共10分.17小题2分,18-19小题个4分,每空2分.)
17.三角形的两边长分别是10和8,则第三边的取值范围是________.
18.一个多边形的内角和是它外角和的3倍,则这个多边形是________边形,内角和是________度。
19.(1)如图,三角形纸片,,,,沿过点的直线折叠这个三角形,使顶点落在边上的点处,折痕为,则的周长为________cm.
(2)如图,点、、、在一条直线上,已知,,请你添加一个适当的条件________使得.
三、解答题(本题共7小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
20.(本小题9.0分)如果一个三角形的一边长为9cm、另一边长为1cm,求:
(1)这个三角形的第三边的范围;
(2)当第三边长为奇数时,求三角形的周长.
21.(本小题9.0分)如图,已知在四边形中,,.
(1)的度数为________;
(2)若的平分线交边于点,且,求的度数.
22.(本小题9.0分)如图,,,,求的度数.
23.(本小题10.0分)已知:如图,,,求证.
24.(本小题10.0分)如图,已知,点在上,与交于点,,,,
(1)求的长度;
(2)求的度数.
25.(本小题12.0分)如图,点,,,在同一条直线上,,相较于点,,,,求证:.
26.(本小题13.0分)(1)如图1,在中,,,是过点的一条直线,且,在的异侧,于点,于点,求证:.
图1
(2)若直线绕点旋转到图2的位置,其余条件不变,则与,之间的数量关系如何?请证明.
图2
(3)若直线绕点旋转到图3的位置,其余条件不变,则与,之间的数量关系如何?请直接写出结果,不需证明.
图3
(4)归纳(1)(2)(3),请用简洁的语言表述与,之间的数量关系.
同课章节目录
