第十二章全等三角形 单元复习题(含解析) 2023—2024学年人教版八年级数学上册
文档属性
| 名称 | 第十二章全等三角形 单元复习题(含解析) 2023—2024学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 516.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 14:55:32 | ||
图片预览



文档简介
人教版八年级数学上册第十二章全等三角形 单元复习题
一、选择题
1.如图,,若,,则的度数为( )
A. B. C. D.
2.全等三角形是( )
A.形状相同的两个三角形 B.周长相等的两个三角形
C.面积相等的两个三角形 D.完全重合的两个三角形
3.如图,已知∠1=∠2,要得到结论ABC≌ADC,不能添加的条件是( )
A.BC=DC B.∠ACB=∠ACD
C.AB=AD D.∠B=∠D
4.用直尺和圆规作一个角等于已知角,如图,能得出∠A'O'B'=∠AOB的依据是( )
A.SAS B.ASA C.AAS D.SSS
5.如图,,,平分,则为( )
A. B. C. D.
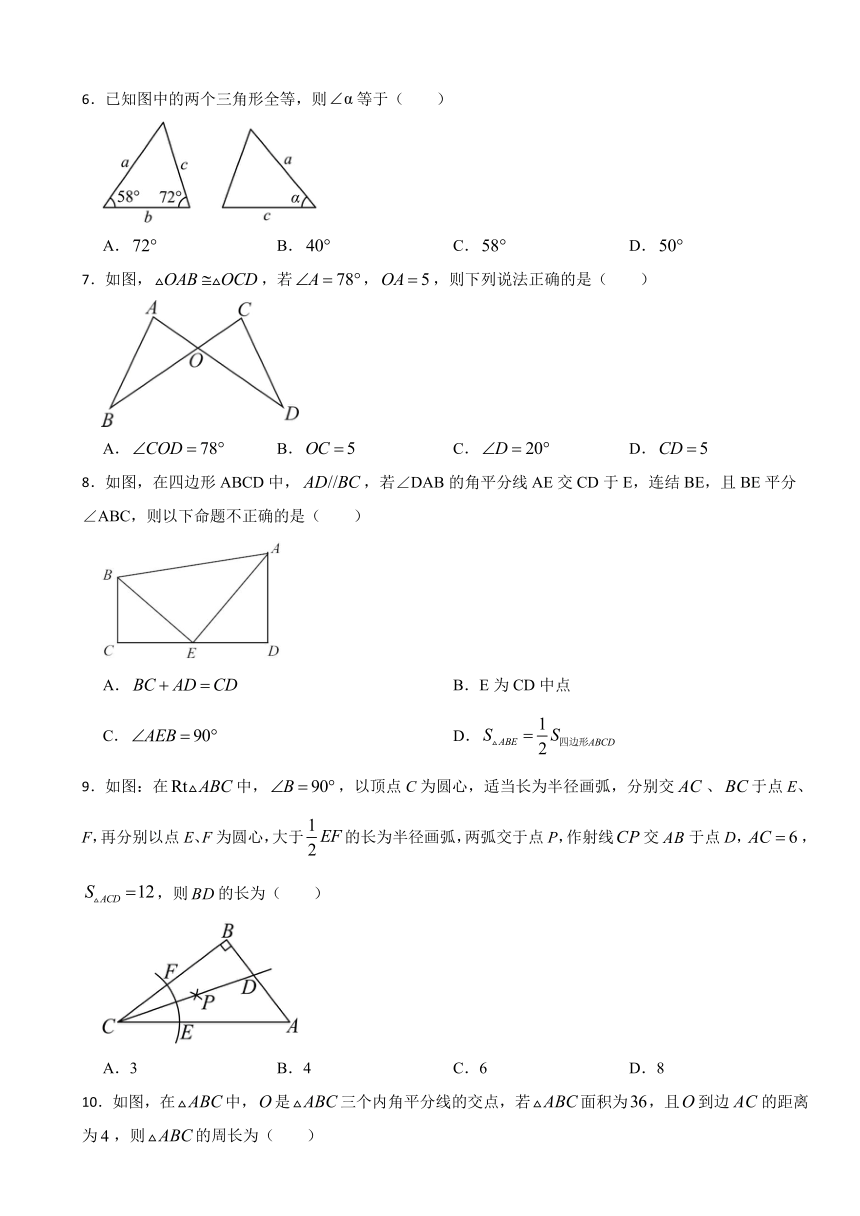
6.已知图中的两个三角形全等,则等于( )
A. B. C. D.
7.如图,,若,,则下列说法正确的是( )
A. B. C. D.
8.如图,在四边形ABCD中,,若∠DAB的角平分线AE交CD于E,连结BE,且BE平分∠ABC,则以下命题不正确的是( )
A. B.E为CD中点
C. D.
9.如图:在中,,以顶点C为圆心,适当长为半径画弧,分别交、于点E、F,再分别以点E、F为圆心,大于的长为半径画弧,两弧交于点P,作射线交于点D,,,则的长为( )
A.3 B.4 C.6 D.8
10.如图,在中,是三个内角平分线的交点,若面积为,且到边的距离为,则的周长为( )
A. B. C. D.
二、填空题
11.如图,在中,,平分交于点,过点作,垂足为点.若,,则的长度为 .
12.一个三角形的三条边的长分别是5,8,10,另一个三角形的三条边的长分别是5,,,若这两个三角形全等,则的值是 .
13. 如图,已知,若以“”为依据证明≌,还需要添加的条件是 .
14.在中,.两条角平分线,所在直线所成的角的度数是 .
三、解答题
15.如图,,求的长.
16.如图是一个工业开发区局部的设计图,河的同一侧有两个工厂A和B,的长表示两个工厂到河岸的距离,其中E是进水口,D、C为污水净化后的出口.已知米,米,求两个排污口之间的水平距离.
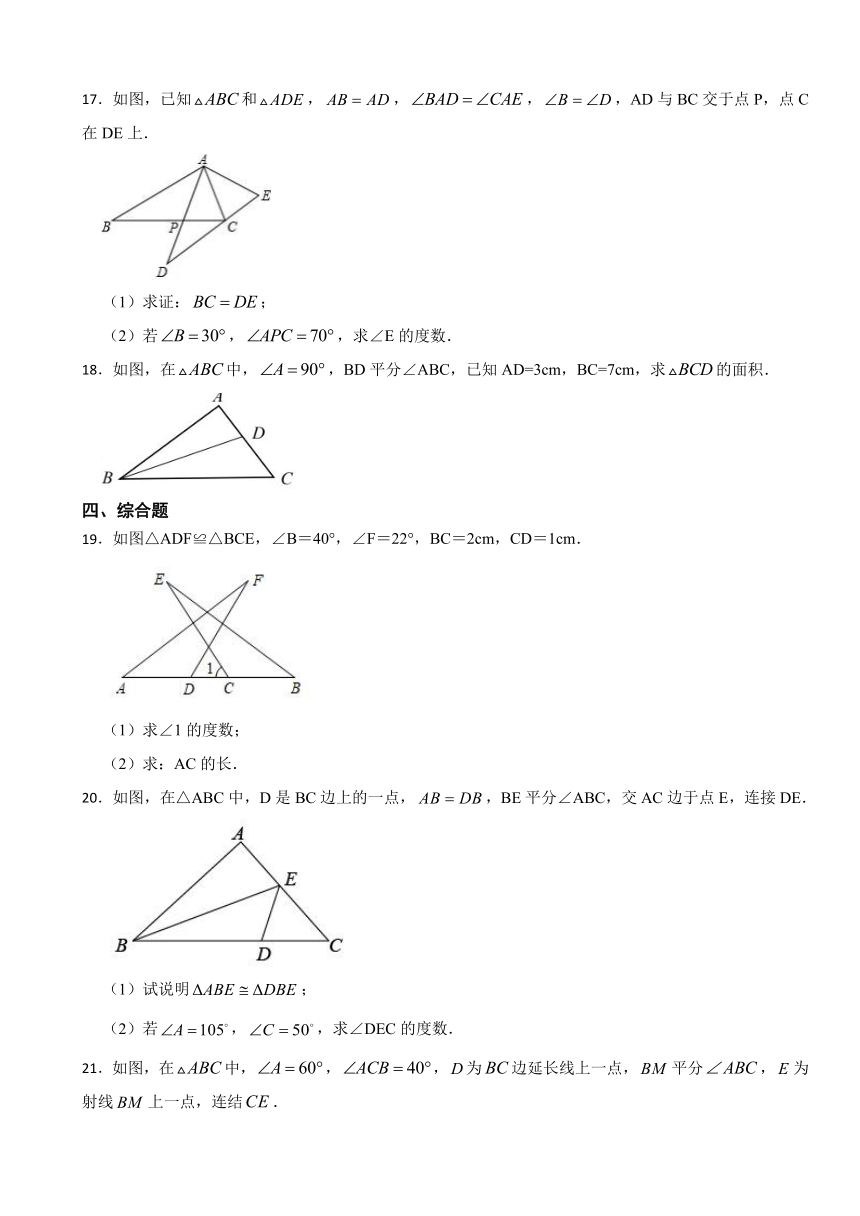
17.如图,已知和,,,,AD与BC交于点P,点C在DE上.
(1)求证:;
(2)若,,求∠E的度数.
18.如图,在中,,BD平分∠ABC,已知AD=3cm,BC=7cm,求的面积.
四、综合题
19.如图△ADF≌△BCE,∠B=40°,∠F=22°,BC=2cm,CD=1cm.
(1)求∠1的度数;
(2)求:AC的长.
20.如图,在△ABC中,D是BC边上的一点,,BE平分∠ABC,交AC边于点E,连接DE.
(1)试说明;
(2)若,,求∠DEC的度数.
21.如图,在中,,,为边延长线上一点,平分,为射线上一点,连结.
(1)求的度数.
(2)若,求的度数.
(3)若平分,求的度数.
答案解析部分
1.【答案】A
【解析】【解答】解:∵
∴∠D=∠B=80°
∵
∴∠E=180°-∠D-∠DAE=30°
故答案为:A
【分析】根据全等三角形的性质及三角形内角和定理即可求出答案。
2.【答案】D
【解析】【解答】解:能够完全重合的两个三角形是全等三角形,故D正确,A、B、C错误。
故答案为:D.
【分析】根据全等三角形的定义判定即可。
3.【答案】A
【解析】【解答】由题意可知,∠1=∠2,AC=AC.
A:BC=DC,添加后,不能证明 ,符合题意;
B:∠ACB=∠ACD,结合题干,通过ASA证明,不合题意;
C:AB=AD,结合题干,通过SAS证明,不合题意;
D:∠B=∠D,结合题干,通过AAS证明,不合题意;
故答案为:A.
【分析】本题考查三角形的全等判定。熟悉三角形全等判定的方法(边边边,边角边,角边角,角角边,斜边直角边(直角三角形))是解题的关键。
4.【答案】D
【解析】【解答】解:由作图痕迹得OC=OD=O′C′=O′D′,CD=C′D′,
∴△C'O'D'≌△COD(SSS),
∴∠A'O'B'=∠AOB.
故答案为:D.
【分析】利用基本作图得到OC=OD=O′C′=O′D′,CD=C′D′,根据三边分别对应相等的两个三角形是全等三角形,全等三角形的对应角相等即可得出答案.
5.【答案】C
【解析】【解答】解:,
,
平分 ,
,
,
.
故答案为:C.
【分析】根据 ,,以及平行线的性质,得到,又由 平分 得到 ,即可求出答.
6.【答案】D
【解析】【解答】解:由题意可得:所对边为b
由第一个图可得:b所对的角度数为:180°-58°-72°=50°
则=50°
故答案为:D.
【分析】根据全等三角形性质及三角形内角和定理即可求出答案。
7.【答案】B
【解析】【解答】解:∵,
∴,故A不符合题意;
度数不确定,故C不符合题意;
∴,故B符合题意;D不符合题意;
故答案为:B.
【分析】利用全等三角形的性质求解即可。
8.【答案】A
9.【答案】B
【解析】【解答】解:过点D作DQ⊥AC于点H
由作图可知:CD是∠ACB的平分线
∵∠B=90°,DH⊥AC
∴DB=DH
∵,AC=6
∴
解得:DH=4
∴BD=DH=4
故答案为:B.
【分析】根据角平分线的性质及三角形面积即可求出答案.
10.【答案】C
【解析】【解答】解:由题意可得:
点O到AB,BC,AC的距离相等
O到边AB,BC的距离都为4
故答案为:C
【分析】根据三角形角平分线性质及面积即可求出答案。
11.【答案】9
【解析】【解答】解:∵平分交于点,,,
∴DE=DC=7,
∵,
∴AD=AC-CD=16-7=9.
故答案为:9.
【分析】利用角平分线上的点到角两边的距离相等可得DE=DC=7,再利用线段的和差求出AD的长即可.
12.【答案】7.5或7
【解析】【解答】解:∵一个三角形的三条边的长分别是5,8,10,另一个三角形的三条边的长分别是5,,,这两个三角形全等,
∴4x+2=8,2y-2=10或4x+2=10,2y-2=8,
解得x=1.5,y=6或x=2,y=5,
∴x+y=7.5或7.
故答案为:7.5或7.
【分析】根据全等三角形的对应边相等可得4x+2=8,2y-2=10或4x+2=10,2y-2=8,求出x、y的值,然后根据有理数的加法法则进行计算.
13.【答案】OA=OD
14.【答案】或
【解析】【解答】解:①当AD,BE是△ABC的内角平分线时,如图
在△ABC中,∠C=60°
∵AD,BE是∠CAB与∠ABC的平分线
②当当AD,BE是△ABC的外角平分线时,如图
在△ABC中,∠C=60°
∵AD,BE是∠FAB与∠GBA的平分线
故答案为:或
【分析】根据角平分线的性质,三角形值得内角与外角性质分情况讨论,即可求出答案.
15.【答案】解:∵,
∴,
∴.
【解析】【分析】根据全等三角形性质即可求出答案.
16.【答案】解:∵,
∴,
∴,
∵,
∴,
∴,
∴米.
【解析】【分析】根据三角形内角和定理,全等三角形判断定理及性质即可求出答案 .
17.【答案】(1)ASA证明全等
(2)70°
18.【答案】
19.【答案】(1)解:∵
∴
由三角形外角的性质可得:
∠1的度数为
(2)解:∵
∴
∴
即AC的长为
【解析】【分析】(1)根据全等三角形的性质可得出,由三角形外角的性质得出 ,即可求解;
(2)由全等三角形的性质得出,即可求解。
20.【答案】(1)解:∵ BE平分∠ABC,
∴.
∵,
∴.
(2)解:∵,
∴,
∴,
∴.
【解析】【分析】(1)根据角平分线的概念可得∠ABE=∠DBE,由已知条件可知AB=DB,然后根据全等三角形的判定定理进行证明;
(2)根据全等三角形的性质可得∠BDE=∠A=105°,根据邻补角的性质可得∠EDC的度数,然后根据内角和定理进行计算即可.
21.【答案】(1)解:∵在中,,,,
∴.
(2)解:由(1)可知,,
∵平分,
∴,
∵,
∴.
(3)解:∵,
∴,,
∴,
∵平分,
∴,
∵平分,
∴,
∵,
∴.
【解析】【分析】(1)先根据三角形内角和定理得到,进而结合题意即可求解;
(2)由(1)可知,进而根据角平分线的性质结合平行线的性质即可求解;
(3)先根据题意得到∠ACD的度数,进而根据角平分线的性质结合题意即可求解。
一、选择题
1.如图,,若,,则的度数为( )
A. B. C. D.
2.全等三角形是( )
A.形状相同的两个三角形 B.周长相等的两个三角形
C.面积相等的两个三角形 D.完全重合的两个三角形
3.如图,已知∠1=∠2,要得到结论ABC≌ADC,不能添加的条件是( )
A.BC=DC B.∠ACB=∠ACD
C.AB=AD D.∠B=∠D
4.用直尺和圆规作一个角等于已知角,如图,能得出∠A'O'B'=∠AOB的依据是( )
A.SAS B.ASA C.AAS D.SSS
5.如图,,,平分,则为( )
A. B. C. D.
6.已知图中的两个三角形全等,则等于( )
A. B. C. D.
7.如图,,若,,则下列说法正确的是( )
A. B. C. D.
8.如图,在四边形ABCD中,,若∠DAB的角平分线AE交CD于E,连结BE,且BE平分∠ABC,则以下命题不正确的是( )
A. B.E为CD中点
C. D.
9.如图:在中,,以顶点C为圆心,适当长为半径画弧,分别交、于点E、F,再分别以点E、F为圆心,大于的长为半径画弧,两弧交于点P,作射线交于点D,,,则的长为( )
A.3 B.4 C.6 D.8
10.如图,在中,是三个内角平分线的交点,若面积为,且到边的距离为,则的周长为( )
A. B. C. D.
二、填空题
11.如图,在中,,平分交于点,过点作,垂足为点.若,,则的长度为 .
12.一个三角形的三条边的长分别是5,8,10,另一个三角形的三条边的长分别是5,,,若这两个三角形全等,则的值是 .
13. 如图,已知,若以“”为依据证明≌,还需要添加的条件是 .
14.在中,.两条角平分线,所在直线所成的角的度数是 .
三、解答题
15.如图,,求的长.
16.如图是一个工业开发区局部的设计图,河的同一侧有两个工厂A和B,的长表示两个工厂到河岸的距离,其中E是进水口,D、C为污水净化后的出口.已知米,米,求两个排污口之间的水平距离.
17.如图,已知和,,,,AD与BC交于点P,点C在DE上.
(1)求证:;
(2)若,,求∠E的度数.
18.如图,在中,,BD平分∠ABC,已知AD=3cm,BC=7cm,求的面积.
四、综合题
19.如图△ADF≌△BCE,∠B=40°,∠F=22°,BC=2cm,CD=1cm.
(1)求∠1的度数;
(2)求:AC的长.
20.如图,在△ABC中,D是BC边上的一点,,BE平分∠ABC,交AC边于点E,连接DE.
(1)试说明;
(2)若,,求∠DEC的度数.
21.如图,在中,,,为边延长线上一点,平分,为射线上一点,连结.
(1)求的度数.
(2)若,求的度数.
(3)若平分,求的度数.
答案解析部分
1.【答案】A
【解析】【解答】解:∵
∴∠D=∠B=80°
∵
∴∠E=180°-∠D-∠DAE=30°
故答案为:A
【分析】根据全等三角形的性质及三角形内角和定理即可求出答案。
2.【答案】D
【解析】【解答】解:能够完全重合的两个三角形是全等三角形,故D正确,A、B、C错误。
故答案为:D.
【分析】根据全等三角形的定义判定即可。
3.【答案】A
【解析】【解答】由题意可知,∠1=∠2,AC=AC.
A:BC=DC,添加后,不能证明 ,符合题意;
B:∠ACB=∠ACD,结合题干,通过ASA证明,不合题意;
C:AB=AD,结合题干,通过SAS证明,不合题意;
D:∠B=∠D,结合题干,通过AAS证明,不合题意;
故答案为:A.
【分析】本题考查三角形的全等判定。熟悉三角形全等判定的方法(边边边,边角边,角边角,角角边,斜边直角边(直角三角形))是解题的关键。
4.【答案】D
【解析】【解答】解:由作图痕迹得OC=OD=O′C′=O′D′,CD=C′D′,
∴△C'O'D'≌△COD(SSS),
∴∠A'O'B'=∠AOB.
故答案为:D.
【分析】利用基本作图得到OC=OD=O′C′=O′D′,CD=C′D′,根据三边分别对应相等的两个三角形是全等三角形,全等三角形的对应角相等即可得出答案.
5.【答案】C
【解析】【解答】解:,
,
平分 ,
,
,
.
故答案为:C.
【分析】根据 ,,以及平行线的性质,得到,又由 平分 得到 ,即可求出答.
6.【答案】D
【解析】【解答】解:由题意可得:所对边为b
由第一个图可得:b所对的角度数为:180°-58°-72°=50°
则=50°
故答案为:D.
【分析】根据全等三角形性质及三角形内角和定理即可求出答案。
7.【答案】B
【解析】【解答】解:∵,
∴,故A不符合题意;
度数不确定,故C不符合题意;
∴,故B符合题意;D不符合题意;
故答案为:B.
【分析】利用全等三角形的性质求解即可。
8.【答案】A
9.【答案】B
【解析】【解答】解:过点D作DQ⊥AC于点H
由作图可知:CD是∠ACB的平分线
∵∠B=90°,DH⊥AC
∴DB=DH
∵,AC=6
∴
解得:DH=4
∴BD=DH=4
故答案为:B.
【分析】根据角平分线的性质及三角形面积即可求出答案.
10.【答案】C
【解析】【解答】解:由题意可得:
点O到AB,BC,AC的距离相等
O到边AB,BC的距离都为4
故答案为:C
【分析】根据三角形角平分线性质及面积即可求出答案。
11.【答案】9
【解析】【解答】解:∵平分交于点,,,
∴DE=DC=7,
∵,
∴AD=AC-CD=16-7=9.
故答案为:9.
【分析】利用角平分线上的点到角两边的距离相等可得DE=DC=7,再利用线段的和差求出AD的长即可.
12.【答案】7.5或7
【解析】【解答】解:∵一个三角形的三条边的长分别是5,8,10,另一个三角形的三条边的长分别是5,,,这两个三角形全等,
∴4x+2=8,2y-2=10或4x+2=10,2y-2=8,
解得x=1.5,y=6或x=2,y=5,
∴x+y=7.5或7.
故答案为:7.5或7.
【分析】根据全等三角形的对应边相等可得4x+2=8,2y-2=10或4x+2=10,2y-2=8,求出x、y的值,然后根据有理数的加法法则进行计算.
13.【答案】OA=OD
14.【答案】或
【解析】【解答】解:①当AD,BE是△ABC的内角平分线时,如图
在△ABC中,∠C=60°
∵AD,BE是∠CAB与∠ABC的平分线
②当当AD,BE是△ABC的外角平分线时,如图
在△ABC中,∠C=60°
∵AD,BE是∠FAB与∠GBA的平分线
故答案为:或
【分析】根据角平分线的性质,三角形值得内角与外角性质分情况讨论,即可求出答案.
15.【答案】解:∵,
∴,
∴.
【解析】【分析】根据全等三角形性质即可求出答案.
16.【答案】解:∵,
∴,
∴,
∵,
∴,
∴,
∴米.
【解析】【分析】根据三角形内角和定理,全等三角形判断定理及性质即可求出答案 .
17.【答案】(1)ASA证明全等
(2)70°
18.【答案】
19.【答案】(1)解:∵
∴
由三角形外角的性质可得:
∠1的度数为
(2)解:∵
∴
∴
即AC的长为
【解析】【分析】(1)根据全等三角形的性质可得出,由三角形外角的性质得出 ,即可求解;
(2)由全等三角形的性质得出,即可求解。
20.【答案】(1)解:∵ BE平分∠ABC,
∴.
∵,
∴.
(2)解:∵,
∴,
∴,
∴.
【解析】【分析】(1)根据角平分线的概念可得∠ABE=∠DBE,由已知条件可知AB=DB,然后根据全等三角形的判定定理进行证明;
(2)根据全等三角形的性质可得∠BDE=∠A=105°,根据邻补角的性质可得∠EDC的度数,然后根据内角和定理进行计算即可.
21.【答案】(1)解:∵在中,,,,
∴.
(2)解:由(1)可知,,
∵平分,
∴,
∵,
∴.
(3)解:∵,
∴,,
∴,
∵平分,
∴,
∵平分,
∴,
∵,
∴.
【解析】【分析】(1)先根据三角形内角和定理得到,进而结合题意即可求解;
(2)由(1)可知,进而根据角平分线的性质结合平行线的性质即可求解;
(3)先根据题意得到∠ACD的度数,进而根据角平分线的性质结合题意即可求解。
