人教版八年级数学上册试题 第十二章 全等三角形单元测试卷(含答案)
文档属性
| 名称 | 人教版八年级数学上册试题 第十二章 全等三角形单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 15:17:35 | ||
图片预览



文档简介
第十二章 全等三角形单元测试卷
一、选择题(本大题共14个小题,每题2分,共28分)
1.下列说法正确的是( )
A.两个面积相等的图形一定是全等图形 B.两个全等图形形状一定相同
C.两个周长相等的图形一定是全等图形 D.两个正三角形一定是全等图形
2.如图,△AOC≌△DOB,AO=3,则下列线段长度正确的是( )
A.AB=3 B.BO=3 C.DB=3 D.DO=3
3.作一个三角形与已知三角形全等:
已知:.
求作:,使得.
作法:如图.
(1)画;
(2)分别以点,为圆心,线段AB,AC长为半径画弧,两弧相交于点;
(3)连接线段,,则即为所求作的三角形.
这种作一个三角形与已知三角形全等的方法的依据是( )
A.AAS B.ASA C.SAS D.SSS
4.如图,若,,,则的度数为( )
A. B. C. D.
5.根据下列已知条件,能唯一画出的是( )
A.,, B.,,
C.,, D.,
6.如图,用尺规作∠AOB的平分线可以按如下步骤进行:①以点O为圆心,线段m为半径画弧,交OA于点M,交OB于点N;②分别以点M,N为圆心,线段n为半径画弧,两弧在∠AOB的内部相交于点C;③画射线OC.射线OC即为所求.以下关于线段m,n的长说法正确的是( )
A.m>0,n>0 B.m>0,n<MN C.m>0,n>MN D.以上都不对
7.如图,已知与,B,E,C,D四点在同一条直线上,其中,,,则等于( )
A. B. C. D.
8.在中,,分别是、上的点,过点作,,垂足分别是点,,连接,若,,则下面三个结论:①;②;③.其中正确的是( )
A.①③ B.②③ C.①② D.①②③
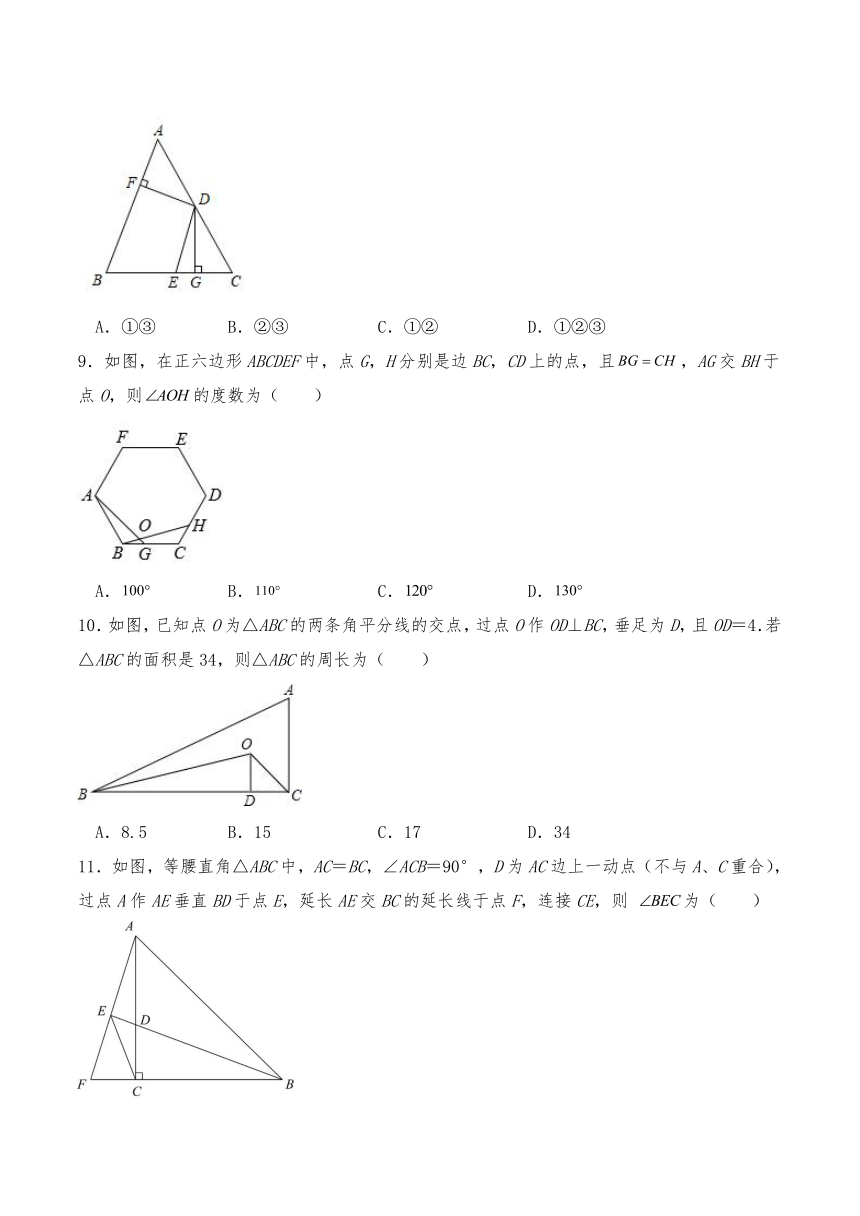
9.如图,在正六边形ABCDEF中,点G,H分别是边BC,CD上的点,且,AG交BH于点O,则的度数为( )
A. B. C. D.
10.如图,已知点O为△ABC的两条角平分线的交点,过点O作OD⊥BC,垂足为D,且OD=4.若△ABC的面积是34,则△ABC的周长为( )
A.8.5 B.15 C.17 D.34
11.如图,等腰直角△ABC中,AC=BC,∠ACB=90°,D为AC边上一动点(不与A、C重合),过点A作AE垂直BD于点E,延长AE交BC的延长线于点F,连接CE,则 为( )
A.30° B.36° C.45° D.60°
12.如图,在中,的平分线交于点D,DE//AB,交于点E,于点F,,则下列结论错误的是( )
A. B. C. D.
13.如图,在四边形中,是的平分线,且.若,则四边形的周长为( )
A. B. C. D.
14.如图,D为的外角平分线上一点并且满足,过D作于E,交BA的延长线于F,则下列结论:
①,②,③,④,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共4个小题;每个小题3分,共12分,把正确答案填在横线上)
15.一个三角形的三条边的长分别是5,8,10,另一个三角形的三条边的长分别是5,,,若这两个三角形全等,则的值是________.
16.如图,在和中,A、F、C、D在同一直线上,,,当添加条件______时,就可得到(只需填一个你认为正确的条件即可).
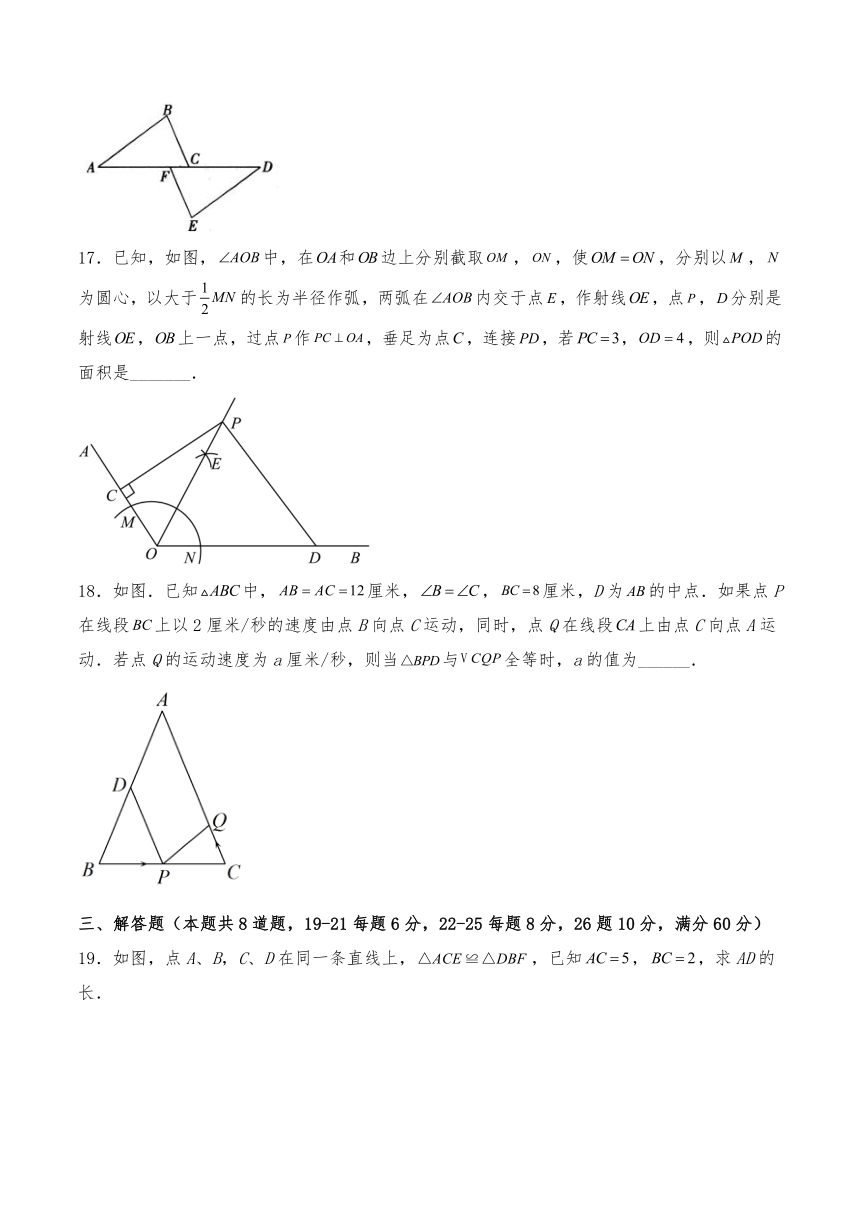
17.已知,如图,中,在和边上分别截取,,使,分别以,为圆心,以大于的长为半径作弧,两弧在内交于点,作射线,点,分别是射线,上一点,过点作,垂足为点,连接,若,,则的面积是_______.
18.如图.已知中,厘米,,厘米,D为的中点.如果点P在线段上以2厘米/秒的速度由点B向点C运动,同时,点Q在线段上由点C向点A运动.若点Q的运动速度为a厘米/秒,则当与全等时,a的值为______.
三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)
19.如图,点A、B,C、D在同一条直线上,,已知,,求AD的长.
20.如图,已知CD⊥AB,BE⊥AC,垂足分别为点D,E,且AB=AC,BE交CD于点O.
(1)求证:DB=EC.
(2)求证:AO平分∠BAC.
21.如图,已知中,是的角平分线,于E点.
(1)求的度数;
(2)若,求.
22.已知:,,,垂足分别为D,E,且BD,CE相交于点F.
(1)如图①,求证:.
(2)如图②,连接AF,在不添加任何辅助线的情况下,写出图中的全等三角形(至少写出两对).
23.已知,在中,,.
(1)在BC上找一点E,使得点E到AB,AC的距离相等(尺规作图,保留痕迹)
(2)若,求的度数.
24.如图,四边形ACDB中,∠D=∠ABD=90°,点O为BD的中点,且AO平分∠BAC,OE⊥AC,垂足为点E.
(1)求证:CO平分∠ACD;
(2)求证:OA⊥OC;
(3)判断AB,CD,AC之间的数量关系,并说明理由.
25.已知:在中,于点D,于点E,与交于点G.
(1)如图,求证:;
(2)如图,若,求证:;
(3)如图,在(2)的条件下,连接,若,求四边形的面积.
26.通过对下面数学模型的研究学习,解决下列问题:
【模型呈现】(1)如图1,,,过点作于点,过点作于点.由,得.又,可以推理得到.进而得到 , .我们把这个数学模型称为“字”模型或“一线三等角”模型;
【模型应用】(2)①如图2,,,,连接,,且于点,与直线交于点.求证:点是的中点;
②如图3,在平面直角坐标系中,点的坐标为,点为平面内任一点.若是以为斜边的等腰直角三角形,请直接写出点的坐标.
答案
一、选择题
B.D.D.B.A.C.D.C.C.C.CA.B.D
二、填空题
15.7.5或7.
16.BC=EF或∠A=∠D(任写一个即可)
17.6.
18.2或3.
三、解答题
19.
解:,
.
,,
,
.
20.
(1)证明:∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°,
在△ADC和△AEB中,
,
∴△ADC≌△AEB(AAS),
∴AD=AE,
∴AB﹣AD=AC﹣AE,
即DB=EC;
(2)证明:∵CD⊥AB,BE⊥AC,
∴∠BDO=∠CEO=90°,
在△BDO和△CEO中,
,
∴△BDO≌△CEO(AAS),
∴OD=OE,
∵CD⊥AB,BE⊥AC,
∴AO平分∠BAC.
21.
(1)解:∵,
∴,
∵是的角平分线,
∴,
∵,∴,
∴;
(2)解∶如图,过D作于F.
∵是的角平分线,,∴,
又∵,且,
∴.
22.
(1)
证明:∵,,
∴,
∵,,
∴,
∴.
(2)△BEF≌△CDF,△AEF≌△ADF;
证明:由(1)可知,
∵,
∴BE=DC,
∵,
∴∠B=∠C,
∵∠CDF=∠BEF=90°,
∴△BEF≌△CDF(ASA),
∴EF=DF,
∵AF=AF,,
∴△AEF≌△ADF(HL).
23.
解:(1)如图,点为所作;
(2)点到,的距离相等,
点在的平分线上,即平分,
∴∠CAE=∠BAE=350
∴∠BAC=2×350 =700
∴∠C=∠B-∠BAC=900-700=200
24.
(1)证明:∵∠ABD=90°,OA平分∠BAC,OE⊥AC,
∴OB=OE,
∵点O为BD的中点,
∴OB=OD,
∴OE=OD,
又∵EO⊥AC,∠D=90°,
∴OC平分∠ACD.
(2)证明:在Rt△ABO和Rt△AEO中,
,
∴Rt△ABO≌Rt△AEO(HL),
∴∠AOB=∠AOE,
同理求出∠COD=∠COE,
∴∠AOC=∠AOE+∠COE=×180°=90°,
∴OA⊥OC.
(3)结论:AB+CD=AC.
理由:∵Rt△ABO≌Rt△AEO,
∴AB=AE,
同理可得CD=CE,
∵AC=AE+CE,
∴AB+CD=AC.
故答案为:AB+CD=AC.
25.
(1)证明:∵,
∴和是直角三角形.
在和中,
,,
∵,∴;
(2)证明:∵,,
∴.
在和中,,
∴,∴;
(3)解:过点D作交于点F,如图所示
,
∵,,
∴.
由(2)可知:
∴,
在和中,,
∴,
∴,
∴ ,
∴.
26.
解:(1)AC=DE,BC=AE;
故答案为:,
(2)①如图,作于,于,
∵,
∴,
∵,
∴,
∴,
在与中,,,,
∴(),
∴,
同理,
∴,
∵,,
∴,
在与中,,,,
∴(),
∴,
∴点是的中点;
②如图,过A作AM⊥y轴,过B作BN⊥x轴于N,AM与BN相交于M,
∴∠M=90°,
∵∠OBA=90°,
∴∠ABM+∠OBN=90°,
∵∠ABM+∠BAM=90°,
∴∠OBN=∠BAM,
在△OBN与△BAM中, ,
∴△OBN≌△BAM(AAS),
∴AM=BN,ON=BM,
设AM=x,则BN=AM=x,
∴ON= x+2,
∴MB+NB=x+x+2=MN=4,
∴x=1,x+2=3,
∴点B的坐标(3,1);
如图
同理可得,点B的坐标(-1,3),
综上所述,点B的坐标为,
一、选择题(本大题共14个小题,每题2分,共28分)
1.下列说法正确的是( )
A.两个面积相等的图形一定是全等图形 B.两个全等图形形状一定相同
C.两个周长相等的图形一定是全等图形 D.两个正三角形一定是全等图形
2.如图,△AOC≌△DOB,AO=3,则下列线段长度正确的是( )
A.AB=3 B.BO=3 C.DB=3 D.DO=3
3.作一个三角形与已知三角形全等:
已知:.
求作:,使得.
作法:如图.
(1)画;
(2)分别以点,为圆心,线段AB,AC长为半径画弧,两弧相交于点;
(3)连接线段,,则即为所求作的三角形.
这种作一个三角形与已知三角形全等的方法的依据是( )
A.AAS B.ASA C.SAS D.SSS
4.如图,若,,,则的度数为( )
A. B. C. D.
5.根据下列已知条件,能唯一画出的是( )
A.,, B.,,
C.,, D.,
6.如图,用尺规作∠AOB的平分线可以按如下步骤进行:①以点O为圆心,线段m为半径画弧,交OA于点M,交OB于点N;②分别以点M,N为圆心,线段n为半径画弧,两弧在∠AOB的内部相交于点C;③画射线OC.射线OC即为所求.以下关于线段m,n的长说法正确的是( )
A.m>0,n>0 B.m>0,n<MN C.m>0,n>MN D.以上都不对
7.如图,已知与,B,E,C,D四点在同一条直线上,其中,,,则等于( )
A. B. C. D.
8.在中,,分别是、上的点,过点作,,垂足分别是点,,连接,若,,则下面三个结论:①;②;③.其中正确的是( )
A.①③ B.②③ C.①② D.①②③
9.如图,在正六边形ABCDEF中,点G,H分别是边BC,CD上的点,且,AG交BH于点O,则的度数为( )
A. B. C. D.
10.如图,已知点O为△ABC的两条角平分线的交点,过点O作OD⊥BC,垂足为D,且OD=4.若△ABC的面积是34,则△ABC的周长为( )
A.8.5 B.15 C.17 D.34
11.如图,等腰直角△ABC中,AC=BC,∠ACB=90°,D为AC边上一动点(不与A、C重合),过点A作AE垂直BD于点E,延长AE交BC的延长线于点F,连接CE,则 为( )
A.30° B.36° C.45° D.60°
12.如图,在中,的平分线交于点D,DE//AB,交于点E,于点F,,则下列结论错误的是( )
A. B. C. D.
13.如图,在四边形中,是的平分线,且.若,则四边形的周长为( )
A. B. C. D.
14.如图,D为的外角平分线上一点并且满足,过D作于E,交BA的延长线于F,则下列结论:
①,②,③,④,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共4个小题;每个小题3分,共12分,把正确答案填在横线上)
15.一个三角形的三条边的长分别是5,8,10,另一个三角形的三条边的长分别是5,,,若这两个三角形全等,则的值是________.
16.如图,在和中,A、F、C、D在同一直线上,,,当添加条件______时,就可得到(只需填一个你认为正确的条件即可).
17.已知,如图,中,在和边上分别截取,,使,分别以,为圆心,以大于的长为半径作弧,两弧在内交于点,作射线,点,分别是射线,上一点,过点作,垂足为点,连接,若,,则的面积是_______.
18.如图.已知中,厘米,,厘米,D为的中点.如果点P在线段上以2厘米/秒的速度由点B向点C运动,同时,点Q在线段上由点C向点A运动.若点Q的运动速度为a厘米/秒,则当与全等时,a的值为______.
三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)
19.如图,点A、B,C、D在同一条直线上,,已知,,求AD的长.
20.如图,已知CD⊥AB,BE⊥AC,垂足分别为点D,E,且AB=AC,BE交CD于点O.
(1)求证:DB=EC.
(2)求证:AO平分∠BAC.
21.如图,已知中,是的角平分线,于E点.
(1)求的度数;
(2)若,求.
22.已知:,,,垂足分别为D,E,且BD,CE相交于点F.
(1)如图①,求证:.
(2)如图②,连接AF,在不添加任何辅助线的情况下,写出图中的全等三角形(至少写出两对).
23.已知,在中,,.
(1)在BC上找一点E,使得点E到AB,AC的距离相等(尺规作图,保留痕迹)
(2)若,求的度数.
24.如图,四边形ACDB中,∠D=∠ABD=90°,点O为BD的中点,且AO平分∠BAC,OE⊥AC,垂足为点E.
(1)求证:CO平分∠ACD;
(2)求证:OA⊥OC;
(3)判断AB,CD,AC之间的数量关系,并说明理由.
25.已知:在中,于点D,于点E,与交于点G.
(1)如图,求证:;
(2)如图,若,求证:;
(3)如图,在(2)的条件下,连接,若,求四边形的面积.
26.通过对下面数学模型的研究学习,解决下列问题:
【模型呈现】(1)如图1,,,过点作于点,过点作于点.由,得.又,可以推理得到.进而得到 , .我们把这个数学模型称为“字”模型或“一线三等角”模型;
【模型应用】(2)①如图2,,,,连接,,且于点,与直线交于点.求证:点是的中点;
②如图3,在平面直角坐标系中,点的坐标为,点为平面内任一点.若是以为斜边的等腰直角三角形,请直接写出点的坐标.
答案
一、选择题
B.D.D.B.A.C.D.C.C.C.CA.B.D
二、填空题
15.7.5或7.
16.BC=EF或∠A=∠D(任写一个即可)
17.6.
18.2或3.
三、解答题
19.
解:,
.
,,
,
.
20.
(1)证明:∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°,
在△ADC和△AEB中,
,
∴△ADC≌△AEB(AAS),
∴AD=AE,
∴AB﹣AD=AC﹣AE,
即DB=EC;
(2)证明:∵CD⊥AB,BE⊥AC,
∴∠BDO=∠CEO=90°,
在△BDO和△CEO中,
,
∴△BDO≌△CEO(AAS),
∴OD=OE,
∵CD⊥AB,BE⊥AC,
∴AO平分∠BAC.
21.
(1)解:∵,
∴,
∵是的角平分线,
∴,
∵,∴,
∴;
(2)解∶如图,过D作于F.
∵是的角平分线,,∴,
又∵,且,
∴.
22.
(1)
证明:∵,,
∴,
∵,,
∴,
∴.
(2)△BEF≌△CDF,△AEF≌△ADF;
证明:由(1)可知,
∵,
∴BE=DC,
∵,
∴∠B=∠C,
∵∠CDF=∠BEF=90°,
∴△BEF≌△CDF(ASA),
∴EF=DF,
∵AF=AF,,
∴△AEF≌△ADF(HL).
23.
解:(1)如图,点为所作;
(2)点到,的距离相等,
点在的平分线上,即平分,
∴∠CAE=∠BAE=350
∴∠BAC=2×350 =700
∴∠C=∠B-∠BAC=900-700=200
24.
(1)证明:∵∠ABD=90°,OA平分∠BAC,OE⊥AC,
∴OB=OE,
∵点O为BD的中点,
∴OB=OD,
∴OE=OD,
又∵EO⊥AC,∠D=90°,
∴OC平分∠ACD.
(2)证明:在Rt△ABO和Rt△AEO中,
,
∴Rt△ABO≌Rt△AEO(HL),
∴∠AOB=∠AOE,
同理求出∠COD=∠COE,
∴∠AOC=∠AOE+∠COE=×180°=90°,
∴OA⊥OC.
(3)结论:AB+CD=AC.
理由:∵Rt△ABO≌Rt△AEO,
∴AB=AE,
同理可得CD=CE,
∵AC=AE+CE,
∴AB+CD=AC.
故答案为:AB+CD=AC.
25.
(1)证明:∵,
∴和是直角三角形.
在和中,
,,
∵,∴;
(2)证明:∵,,
∴.
在和中,,
∴,∴;
(3)解:过点D作交于点F,如图所示
,
∵,,
∴.
由(2)可知:
∴,
在和中,,
∴,
∴,
∴ ,
∴.
26.
解:(1)AC=DE,BC=AE;
故答案为:,
(2)①如图,作于,于,
∵,
∴,
∵,
∴,
∴,
在与中,,,,
∴(),
∴,
同理,
∴,
∵,,
∴,
在与中,,,,
∴(),
∴,
∴点是的中点;
②如图,过A作AM⊥y轴,过B作BN⊥x轴于N,AM与BN相交于M,
∴∠M=90°,
∵∠OBA=90°,
∴∠ABM+∠OBN=90°,
∵∠ABM+∠BAM=90°,
∴∠OBN=∠BAM,
在△OBN与△BAM中, ,
∴△OBN≌△BAM(AAS),
∴AM=BN,ON=BM,
设AM=x,则BN=AM=x,
∴ON= x+2,
∴MB+NB=x+x+2=MN=4,
∴x=1,x+2=3,
∴点B的坐标(3,1);
如图
同理可得,点B的坐标(-1,3),
综上所述,点B的坐标为,
