人教版八年级数学上册试题 第十一章 三角形单元测试卷(含答案)
文档属性
| 名称 | 人教版八年级数学上册试题 第十一章 三角形单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 15:18:28 | ||
图片预览



文档简介
第十一章 三角形单元测试卷
一、选择题(本大题共14个小题,每题2分,共28分,)
1.如图,以AB为边的三角形的个数是( )
A.1 个 B.2 个 C.3 个 D.4 个
2.三角形的两条边长分别为3 cm和6 cm,下列长度中,可能是这个三角形第三条边的是( )
A.1 cm B.3 cm C.5 cm D.10 cm
3.在△ABC中,AD、AE、AF分别是它的高线、角平分线和中线,则下列说法中错误的是( )
A. B. C. D.
4.如图,、都是的角平分线,且,则( )
A.45° B.50° C.65° D.70°
5.木工师傅要使一个四边形木架(用四根木条钉成)不变型,至少要再钉上n根木条,这里的n=( )
A.0 B.1 C.2 D.3
6.如图,BC⊥AE于点C,CDAB,∠DCB=40°,则∠A的度数是( )
A.70° B.60° C.50° D.40°
7.在△ABC中,,则△ABC的形状是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.形状无法确定
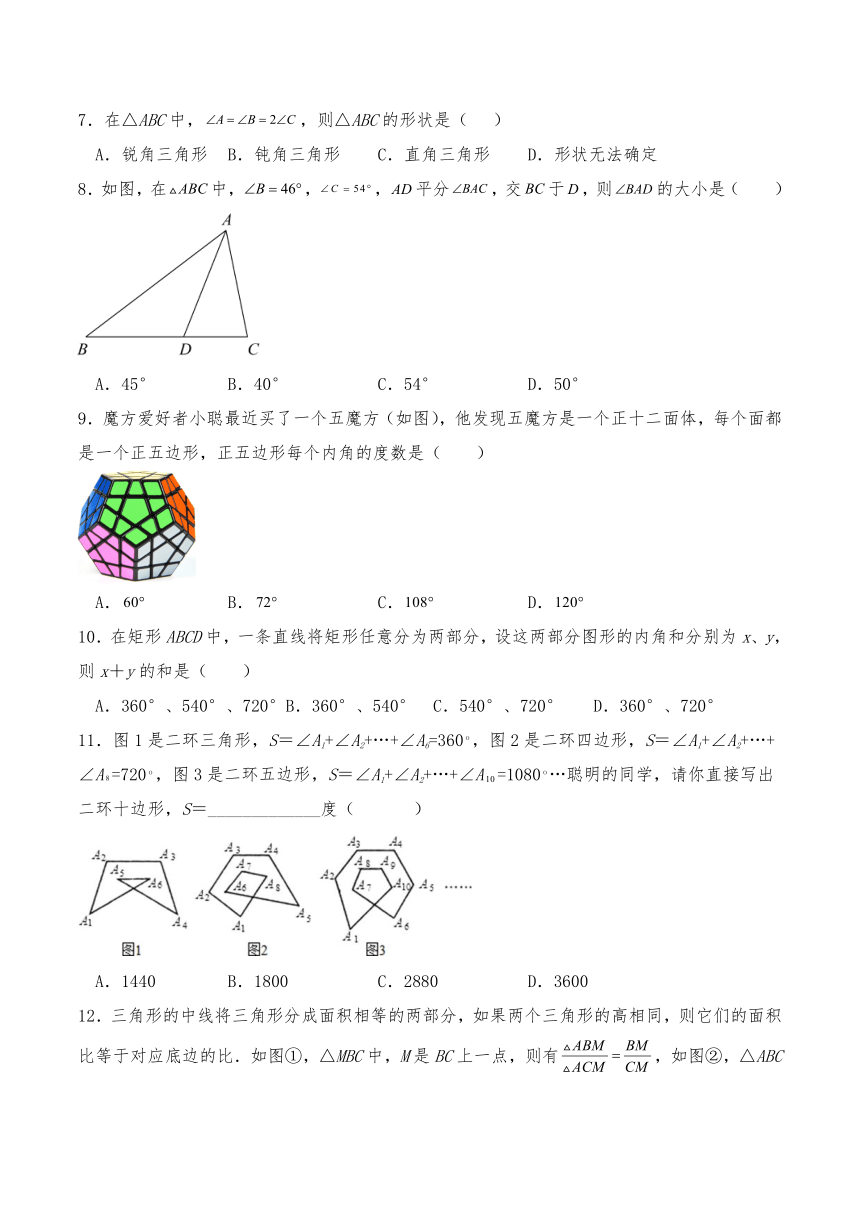
8.如图,在中,,,平分,交于,则的大小是( )
A.45° B.40° C.54° D.50°
9.魔方爱好者小聪最近买了一个五魔方(如图),他发现五魔方是一个正十二面体,每个面都是一个正五边形,正五边形每个内角的度数是( )
A. B. C. D.
10.在矩形ABCD中,一条直线将矩形任意分为两部分,设这两部分图形的内角和分别为x、y,则x+y的和是( )
A.360°、540°、720°B.360°、540° C.540°、720° D.360°、720°
11.图1是二环三角形,S=∠A1+∠A2+…+∠A6=360,图2是二环四边形,S=∠A1+∠A2+…+∠A=720,图3是二环五边形,S=∠A1+∠A2+…+∠A=1080…聪明的同学,请你直接写出二环十边形,S=_____________度( )
A.1440 B.1800 C.2880 D.3600
12.三角形的中线将三角形分成面积相等的两部分,如果两个三角形的高相同,则它们的面积比等于对应底边的比.如图①,△MBC中,M是BC上一点,则有,如图②,△ABC中,M是BC上一点,且BM=BC,N是AC的中点,若△ABC的面积是1,则△ADN的面积是( )
A. B. C. D.
13.如图,直线//,点E、M分别为直线上的点,点N为两平行线间的点,连接,过点N作平分,交直线于点G,过点N作,交直线于点F,若,则的角度等于( ).
A. B. C. D.
14.如图,在中,和的角平分线BE,CF相交于点G,过点E作于点M,交CF于点K,则下列结论一定正确的有( )个.
(1);
(2);
(3);
(4)点P为AB边任意一点,于点Q,PN平分,则.
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共4个小题;每个小题3分,共12分,把正确答案填在横线上)
15.一个多边形外角和是内角和的,则这个多边形的边数为________.
16.如图,点、点是直线上两点,,点在直线外,,,,若点为直线上一动点,连接,则线段的最小值是______.
17.在中,为中点,,设的面积为,的面积为,若的面积为12,则________.
18.在同一平面内,的两边分别与的两边垂直,且比的2倍少,则=________.
三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)
19.已知,的三边长为4,9,.
(1)求的取值范围.
(2)当的周长为偶数时,求.
20.已知一个多边形每个内角都比它相邻外角大60°.
(1)求这个多边形的内角和;
(2)求这个多边形所有对角线的条数.
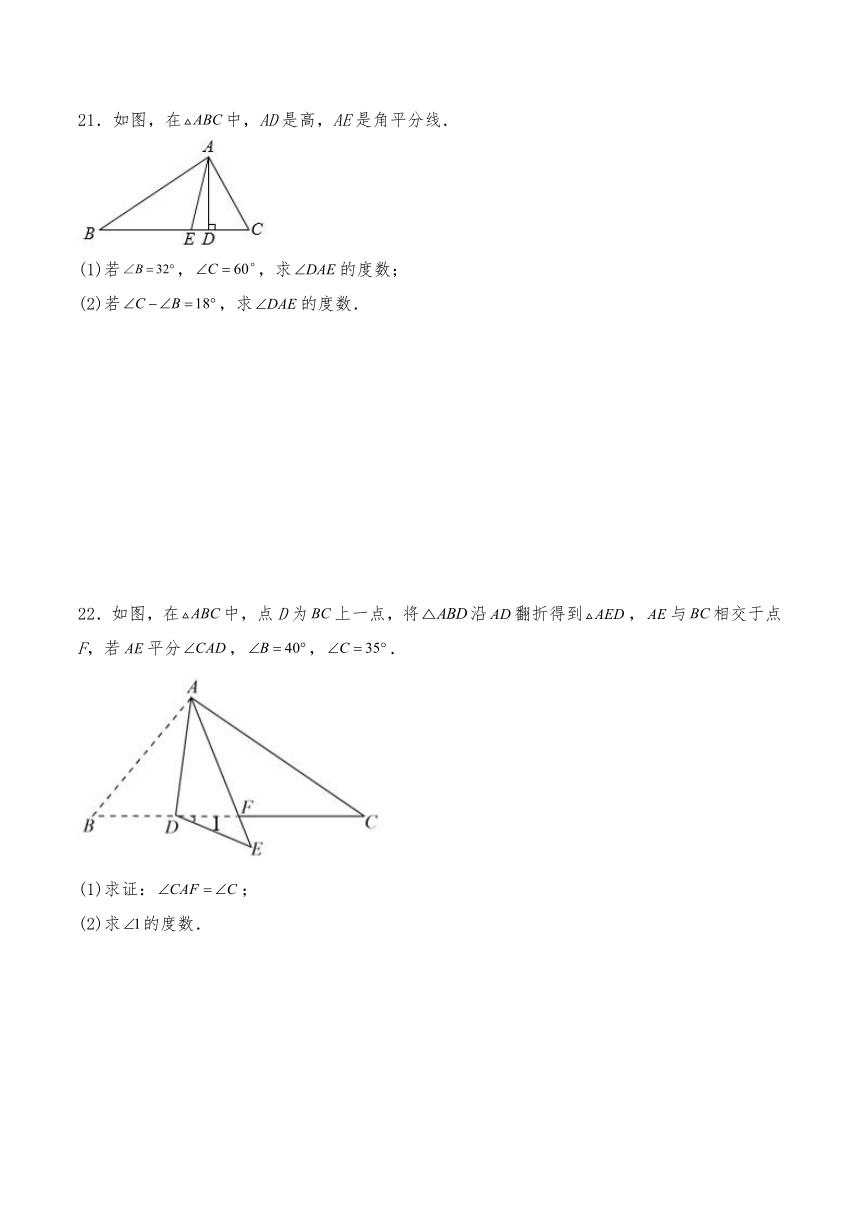
21.如图,在中,AD是高,AE是角平分线.
(1)若,,求的度数;
(2)若,求的度数.
22.如图,在中,点D为上一点,将沿翻折得到,与相交于点F,若平分,,.
(1)求证:;
(2)求的度数.
23.小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为米,由于条件限制,第二条边长只能比第一条边长的3倍少2米.
(1)请用含的式子表示第三条边长;
(2)第一条边长能否为10米?为什么?
(3)直接写出的取值范围.
24.如图,在6×10的网格中,每一小格均为正方形且边长是1,已知△ABC的每个顶点都在格点上.
(1)画出△ABC中BC边上的高线AE;
(2)在△ABC中AB边上取点D,连接CD,使;
(3)直接写出△BCD的面积是__________.
25.【问题提出】在△ABC中,点P是线段BC的中点.在图1中,过点P画一条直线平分△ABC的面积.
【问题探究】育才中学“思维畅想”社团的同学们又研究了这样一个问题:如图2,在△ABC中,点P是线段BC的中点.若点E是线段BP上一点(不与点B、P重合),能否过E作直线平分△ABC的面积?小明给出了如下画法:
(1)作线段AC的中点D;(2)连接DE、BD;(3)过B作BMDE交AC于点M;(4)连接EM,则直线EM平分△ABC的面积.
小明画法正确吗?请你说明理由.
【问题延伸】在四边形ABCD中,点P是AD上一点,请选择图3或图4过点P作直线PQ平分四边形ABCD的面积.
26.折纸是我国一项古老的传统民间艺术,这项具有中国特色的传统文化在几何中可以得到新的解读.已知在△ABC中,∠A=80°,请根据题意,探索不同情境中∠1+∠2(或∠1-∠2)与∠A的数量关系.
(1)如图①,若沿图中虚线DE截去∠A,则∠1+∠2=_______.
(2)如图②,若沿图中虚线DE将∠A翻折,使点A落在BC上的点A’处,则∠1+∠2=_______.
(3)如图③,翻折后,点A落在点A’处,若∠1+∠2=80°,求∠B+∠C的度数
(4)如图④,△ABC纸片沿DE折叠,使点A落在点A’处,若∠1=80°,∠2=24°,求∠A的度数.
答案
一、选择题
D.C.B.B.B.C.A.B.C.A.C.B.B.C.
二、填空题
15.11.
16.4.8
17.2
18.30°或70°
三、解答题
19.
解:(1)∵三角形的三边长分别为4,9,x,
∴9 4<x<9+4,即5<x<13;
(2)∵5<x<13,
∴9+4+5<△ABC的周长<9+4+13,
即:18<△ABC的周长<26;
∵△ABC的周长是偶数,
∴△ABC的周长可以是20,22或24,
∴x的值为7,9或11.
20.
(1)解:设这个多边形为n边形,
由题意得:,
解得,
∴这个多边形的内角和为
(2)解:由(1)得这个多边形为六边形,
∴从六边形的一个顶点出发一共有6-3=3条对角线,
∴这个多边形所有对角线的条数为条.
21.
(1)∵AD是高,AE是角平分线,,,
∴∠DAC=30°,∠BAC=180°-32°-60°=88°,
∴∠EAC=,
∴∠DAE=∠EAC -∠DAC=44°-30°=14°.
(2)∵∠DAE=
=
=
=,,
∴∠DAE=9°.
22.
(1)证明:∵,,
∴,
∵AE平分,
∴,
∵,
∴,
∴,
∴,
(2)解:,
∴,
∵,且,
∴.
23.
(1)∵第二条边长为(3m﹣2)米,
∴第三条边长为50﹣m﹣(3m﹣2)=(52﹣4m)米;
(2)当m=10时,三边长分别为10,28,12,
由于10+12<28,所以不能构成三角形,即第一条边长不能为10米;
(3)根据题意,三角形两边之和大于第三边得:
,
解得<m<9.
24.
(1)解:如图,即为BC上的高.
(2)如图,利用网格特点,可得,
∴D即为所求作的点,满足.
(3).
25.
问题提出:连接AP,直线AP即为所求;
问题探究:由作法可得,S△BDC=S△ABC,
∵BM∥DE,
∴S△BDE=S△MDE ,
∴S△EMC= S△EMD+ S△ECD= S△BDE+ S△ECD =S△ABC,
即EM平分△ABC的面积;
问题延伸:如图所示,
26.
(1)解:∵∠A=80°,
∴∠ADE+∠AED=180°-80°=100°,
∴,
故答案为:260°;
(2)∵∠A=80°,
∴∠ADE+∠AED=180°-80°=100°,
∵翻折,
∴∠EDA’=∠ADE,∠AED=∠DEA’,
∴∠ADA’+∠AEA’=2(∠ADE+∠AED)=200°,
∴∠1+∠2=360°-(∠ADA’+∠AEA’)=160°,
故答案为:160°;
(3)解:连接.如图所示:
∵∠1=∠DAA’+∠DA’A,∠2=∠EAA’+∠EA’A,
∴∠1+∠2=∠DAA’+∠DA’A+∠EAA’+∠EA’A=∠EAD+∠EA’D,
∵,
∴,
∴,
∴.
(4)解:如图,设AB与交于点F,
∵,,
由折叠可得,,
∴,
又∵,,
∴,
∴.
一、选择题(本大题共14个小题,每题2分,共28分,)
1.如图,以AB为边的三角形的个数是( )
A.1 个 B.2 个 C.3 个 D.4 个
2.三角形的两条边长分别为3 cm和6 cm,下列长度中,可能是这个三角形第三条边的是( )
A.1 cm B.3 cm C.5 cm D.10 cm
3.在△ABC中,AD、AE、AF分别是它的高线、角平分线和中线,则下列说法中错误的是( )
A. B. C. D.
4.如图,、都是的角平分线,且,则( )
A.45° B.50° C.65° D.70°
5.木工师傅要使一个四边形木架(用四根木条钉成)不变型,至少要再钉上n根木条,这里的n=( )
A.0 B.1 C.2 D.3
6.如图,BC⊥AE于点C,CDAB,∠DCB=40°,则∠A的度数是( )
A.70° B.60° C.50° D.40°
7.在△ABC中,,则△ABC的形状是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.形状无法确定
8.如图,在中,,,平分,交于,则的大小是( )
A.45° B.40° C.54° D.50°
9.魔方爱好者小聪最近买了一个五魔方(如图),他发现五魔方是一个正十二面体,每个面都是一个正五边形,正五边形每个内角的度数是( )
A. B. C. D.
10.在矩形ABCD中,一条直线将矩形任意分为两部分,设这两部分图形的内角和分别为x、y,则x+y的和是( )
A.360°、540°、720°B.360°、540° C.540°、720° D.360°、720°
11.图1是二环三角形,S=∠A1+∠A2+…+∠A6=360,图2是二环四边形,S=∠A1+∠A2+…+∠A=720,图3是二环五边形,S=∠A1+∠A2+…+∠A=1080…聪明的同学,请你直接写出二环十边形,S=_____________度( )
A.1440 B.1800 C.2880 D.3600
12.三角形的中线将三角形分成面积相等的两部分,如果两个三角形的高相同,则它们的面积比等于对应底边的比.如图①,△MBC中,M是BC上一点,则有,如图②,△ABC中,M是BC上一点,且BM=BC,N是AC的中点,若△ABC的面积是1,则△ADN的面积是( )
A. B. C. D.
13.如图,直线//,点E、M分别为直线上的点,点N为两平行线间的点,连接,过点N作平分,交直线于点G,过点N作,交直线于点F,若,则的角度等于( ).
A. B. C. D.
14.如图,在中,和的角平分线BE,CF相交于点G,过点E作于点M,交CF于点K,则下列结论一定正确的有( )个.
(1);
(2);
(3);
(4)点P为AB边任意一点,于点Q,PN平分,则.
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共4个小题;每个小题3分,共12分,把正确答案填在横线上)
15.一个多边形外角和是内角和的,则这个多边形的边数为________.
16.如图,点、点是直线上两点,,点在直线外,,,,若点为直线上一动点,连接,则线段的最小值是______.
17.在中,为中点,,设的面积为,的面积为,若的面积为12,则________.
18.在同一平面内,的两边分别与的两边垂直,且比的2倍少,则=________.
三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)
19.已知,的三边长为4,9,.
(1)求的取值范围.
(2)当的周长为偶数时,求.
20.已知一个多边形每个内角都比它相邻外角大60°.
(1)求这个多边形的内角和;
(2)求这个多边形所有对角线的条数.
21.如图,在中,AD是高,AE是角平分线.
(1)若,,求的度数;
(2)若,求的度数.
22.如图,在中,点D为上一点,将沿翻折得到,与相交于点F,若平分,,.
(1)求证:;
(2)求的度数.
23.小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为米,由于条件限制,第二条边长只能比第一条边长的3倍少2米.
(1)请用含的式子表示第三条边长;
(2)第一条边长能否为10米?为什么?
(3)直接写出的取值范围.
24.如图,在6×10的网格中,每一小格均为正方形且边长是1,已知△ABC的每个顶点都在格点上.
(1)画出△ABC中BC边上的高线AE;
(2)在△ABC中AB边上取点D,连接CD,使;
(3)直接写出△BCD的面积是__________.
25.【问题提出】在△ABC中,点P是线段BC的中点.在图1中,过点P画一条直线平分△ABC的面积.
【问题探究】育才中学“思维畅想”社团的同学们又研究了这样一个问题:如图2,在△ABC中,点P是线段BC的中点.若点E是线段BP上一点(不与点B、P重合),能否过E作直线平分△ABC的面积?小明给出了如下画法:
(1)作线段AC的中点D;(2)连接DE、BD;(3)过B作BMDE交AC于点M;(4)连接EM,则直线EM平分△ABC的面积.
小明画法正确吗?请你说明理由.
【问题延伸】在四边形ABCD中,点P是AD上一点,请选择图3或图4过点P作直线PQ平分四边形ABCD的面积.
26.折纸是我国一项古老的传统民间艺术,这项具有中国特色的传统文化在几何中可以得到新的解读.已知在△ABC中,∠A=80°,请根据题意,探索不同情境中∠1+∠2(或∠1-∠2)与∠A的数量关系.
(1)如图①,若沿图中虚线DE截去∠A,则∠1+∠2=_______.
(2)如图②,若沿图中虚线DE将∠A翻折,使点A落在BC上的点A’处,则∠1+∠2=_______.
(3)如图③,翻折后,点A落在点A’处,若∠1+∠2=80°,求∠B+∠C的度数
(4)如图④,△ABC纸片沿DE折叠,使点A落在点A’处,若∠1=80°,∠2=24°,求∠A的度数.
答案
一、选择题
D.C.B.B.B.C.A.B.C.A.C.B.B.C.
二、填空题
15.11.
16.4.8
17.2
18.30°或70°
三、解答题
19.
解:(1)∵三角形的三边长分别为4,9,x,
∴9 4<x<9+4,即5<x<13;
(2)∵5<x<13,
∴9+4+5<△ABC的周长<9+4+13,
即:18<△ABC的周长<26;
∵△ABC的周长是偶数,
∴△ABC的周长可以是20,22或24,
∴x的值为7,9或11.
20.
(1)解:设这个多边形为n边形,
由题意得:,
解得,
∴这个多边形的内角和为
(2)解:由(1)得这个多边形为六边形,
∴从六边形的一个顶点出发一共有6-3=3条对角线,
∴这个多边形所有对角线的条数为条.
21.
(1)∵AD是高,AE是角平分线,,,
∴∠DAC=30°,∠BAC=180°-32°-60°=88°,
∴∠EAC=,
∴∠DAE=∠EAC -∠DAC=44°-30°=14°.
(2)∵∠DAE=
=
=
=,,
∴∠DAE=9°.
22.
(1)证明:∵,,
∴,
∵AE平分,
∴,
∵,
∴,
∴,
∴,
(2)解:,
∴,
∵,且,
∴.
23.
(1)∵第二条边长为(3m﹣2)米,
∴第三条边长为50﹣m﹣(3m﹣2)=(52﹣4m)米;
(2)当m=10时,三边长分别为10,28,12,
由于10+12<28,所以不能构成三角形,即第一条边长不能为10米;
(3)根据题意,三角形两边之和大于第三边得:
,
解得<m<9.
24.
(1)解:如图,即为BC上的高.
(2)如图,利用网格特点,可得,
∴D即为所求作的点,满足.
(3).
25.
问题提出:连接AP,直线AP即为所求;
问题探究:由作法可得,S△BDC=S△ABC,
∵BM∥DE,
∴S△BDE=S△MDE ,
∴S△EMC= S△EMD+ S△ECD= S△BDE+ S△ECD =S△ABC,
即EM平分△ABC的面积;
问题延伸:如图所示,
26.
(1)解:∵∠A=80°,
∴∠ADE+∠AED=180°-80°=100°,
∴,
故答案为:260°;
(2)∵∠A=80°,
∴∠ADE+∠AED=180°-80°=100°,
∵翻折,
∴∠EDA’=∠ADE,∠AED=∠DEA’,
∴∠ADA’+∠AEA’=2(∠ADE+∠AED)=200°,
∴∠1+∠2=360°-(∠ADA’+∠AEA’)=160°,
故答案为:160°;
(3)解:连接.如图所示:
∵∠1=∠DAA’+∠DA’A,∠2=∠EAA’+∠EA’A,
∴∠1+∠2=∠DAA’+∠DA’A+∠EAA’+∠EA’A=∠EAD+∠EA’D,
∵,
∴,
∴,
∴.
(4)解:如图,设AB与交于点F,
∵,,
由折叠可得,,
∴,
又∵,,
∴,
∴.
