第4章 图形的平移与旋转 单元测试卷(含解析)2023-2024学年鲁教版(五四制) 数学八年级上册
文档属性
| 名称 | 第4章 图形的平移与旋转 单元测试卷(含解析)2023-2024学年鲁教版(五四制) 数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 764.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 16:13:48 | ||
图片预览

文档简介
鲁教五四新版八年级上学期《第4章 图形的平移与旋转》
一.选择题(共10小题)
1.中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )
A.中国探火CMEP B.中国探月CLEP
C.中国行星探测MARS D.中国火箭CHINAROCKET
2.下列运动属于平移的是( )
A.急刹车时汽车在地面上的滑动
B.冷水加热时小气泡上升变为大气泡
C.电风扇工作时扇叶的转动
D.在百米比赛中,运动员在赛道上的运动
3.第一象限内有两点P(m﹣4,n),Q(m,n﹣2),将线段PQ平移,使平移后的点P、Q分别在x轴与y轴上,则点P平移后的对应点的坐标是( )
A.(﹣4,0) B.(4,0) C.(0,2) D.(0,﹣2)
4.下列图形中,不能通过其中一个图形平移得到的是( )
A. B.
C. D.
5.在俄罗斯方块游戏中,已拼好的图案如图所示,现出现一小方格体正向下运动,你必须进行以下( )操作,才能拼成一个完整图案,使所有图案消失.
A.顺时针旋转90°,向右平移
B.逆时针旋转90°,向右平移
C.顺时针旋转90°,向下平移
D.逆时针旋转90°,向下平移
6.在平面直角坐标系中,点P(m2+1,2)关于原点对称的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A. B. C. D.
8.下面四个图案(忽略旁边一圈的文字):是旋转对称图形的有( )
A.1个 B.2个 C.3个 D.4个
9.如图,在平面直角坐标系中,画△ABC关于点O成中心对称的图形时,由于紧张对称中心选错,画出的图形是△DEF,请你找出此时的对称中心是( )
A.(2,0) B.(2,1) C.(1,2) D.(1,0)
10.如图,将三角尺直立举起靠近墙面,打开手机手电筒照射三角尺,在墙面上形成影子.则三角尺与影子之间属于以下哪种图形变换( )
A.平移 B.轴对称 C.旋转 D.位似
二.填空题(共10小题)
11.在等边三角形、正方形、菱形、等腰梯形中,是中心对称图形的有 .
12.已知点P1(a﹣1,1)和P2(2,b﹣1)关于原点对称,则a+b= .
13.如图,将周长为12的△ABC沿BC边向右平移3个单位,得到△DEF,则四边形ABFD的周长为 .
14.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA、OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E在槽中滑动,若∠BDE=84°,则∠CDE是 °.
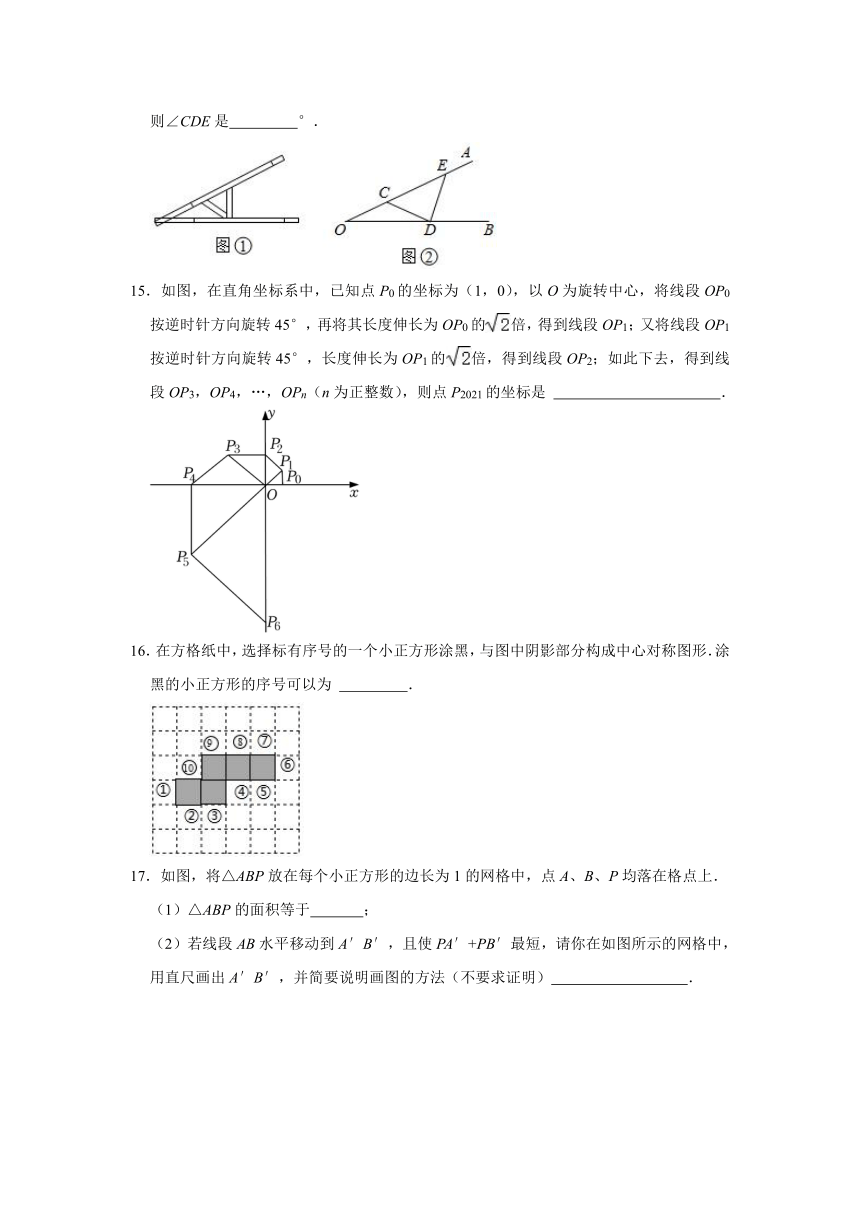
15.如图,在直角坐标系中,已知点P0的坐标为(1,0),以O为旋转中心,将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2021的坐标是 .
16.在方格纸中,选择标有序号的一个小正方形涂黑,与图中阴影部分构成中心对称图形.涂黑的小正方形的序号可以为 .
17.如图,将△ABP放在每个小正方形的边长为1的网格中,点A、B、P均落在格点上.
(1)△ABP的面积等于 ;
(2)若线段AB水平移动到A′B′,且使PA′+PB′最短,请你在如图所示的网格中,用直尺画出A′B′,并简要说明画图的方法(不要求证明) .
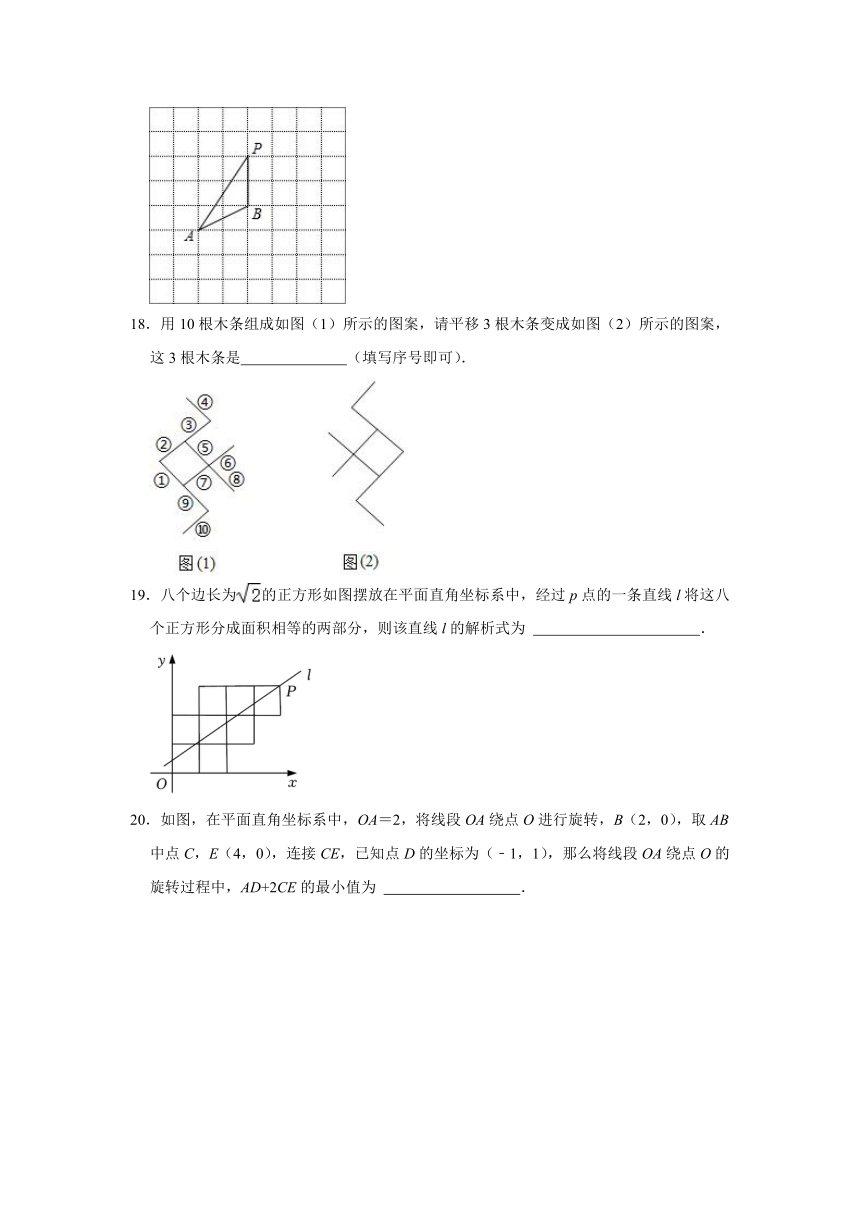
18.用10根木条组成如图(1)所示的图案,请平移3根木条变成如图(2)所示的图案,这3根木条是 (填写序号即可).
19.八个边长为的正方形如图摆放在平面直角坐标系中,经过p点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为 .
20.如图,在平面直角坐标系中,OA=2,将线段OA绕点O进行旋转,B(2,0),取AB中点C,E(4,0),连接CE,已知点D的坐标为(﹣1,1),那么将线段OA绕点O的旋转过程中,AD+2CE的最小值为 .
三.解答题(共7小题)
21.如图,△ABC沿直线l向右平移4cm,得到△FDE,且BC=6cm,∠ABC=45°.
(1)求BE的长.
(2)求∠FDB的度数.
22.如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别为A(﹣2,3),B(﹣3,1),C(0,﹣2).
(1)将△ABC向右平移4个单位后得到△A1B1C1,请画出△A1B1C1;
(2)请直接写出△ABC的面积;
(3)定义:在平面直角坐标系中,横坐标与纵坐标都是整数的点称为“整点”,请直接写出△A1B1C1内部所有的整点的坐标.
23.某宾馆重新装修后,考虑在大厅的主楼梯上铺设地毯.已知主楼梯宽3m,其剖面如图所示,若每平方米地毯售价10元,请你计算一下,仅此楼梯,购买地毯需要多少元?
24.如图,矩形ABCD绕点C顺时针旋转90°后得到矩形FECG,连接DG交EF于点H,连接AF交DG于点M.求证:AM=FM.
25.如图,在直角坐标系内,已知点A(﹣1,0).
(1)图中点B的坐标是 ;
(2)点B关于原点对称的点D的坐标是 ;点A关于y轴对称的点C的坐标是 ;
(3)在y轴上找一点F,使S△ACF=S△ABC.那么点F的坐标为 .
26.如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)画出△ABC关于点O的中心对称图形△A1B1C1;
(2)将△ABC绕坐标原点O逆时针旋转90°,得到△A2B2C2.画出图形,并直接写出点A2、B2、C2的坐标.
27.如图,在△ABC中,AB=AC,∠BAC=90°,过点A作BC的垂线AD,垂足为点D.点E为线段DC上一动点(不与点C重合),连接AE,以点A为中心,将线段AE逆时针旋转90°得到线段AF,连接BF,与线段AD交于点G,连接CF.
(1)依题意补全图形;直接写出BC与CF的位置关系;
(2)求证:;
(3)直接写出AE,BE,AG之间的数量关系.
鲁教五四新版八年级上学期《第4章 图形的平移与旋转》
参考答案与试题解析
一.选择题(共10小题)
1.中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )
A.中国探火CMEP B.中国探月CLEP
C.中国行星探测MARS D.中国火箭CHINAROCKET
【考点】中心对称图形.
【答案】D
【分析】根据中心对称图形的概念判断.把一个图形绕某一点旋转180度,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.
【解答】解:选项A、B、C不都能找到一个点,使图形绕某一点旋转180度后与原来的图形重合,所以不是中心对称图形.
选项D能找到一个点,使图形绕某一点旋转180度后与原来的图形重合,所以是中心对称图形.
故选:D.
2.下列运动属于平移的是( )
A.急刹车时汽车在地面上的滑动
B.冷水加热时小气泡上升变为大气泡
C.电风扇工作时扇叶的转动
D.在百米比赛中,运动员在赛道上的运动
【考点】生活中的平移现象.
【答案】A
【分析】根据平移的性质判断即可.
【解答】解:A、急刹车时汽车在地面上的滑动,属于平移,故A符合题意;
B、冷水加热时小气泡上升变为大气泡,不属于平移,故B不符合题意;
C、电风扇工作时扇叶的转动,属于旋转,故C不符合题意;
D、在百米比赛中,运动员在赛道上的运动,不属于平移,故D不符合题意;
故选:A.
3.第一象限内有两点P(m﹣4,n),Q(m,n﹣2),将线段PQ平移,使平移后的点P、Q分别在x轴与y轴上,则点P平移后的对应点的坐标是( )
A.(﹣4,0) B.(4,0) C.(0,2) D.(0,﹣2)
【考点】坐标与图形变化﹣平移.
【答案】A
【分析】根据平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减解答即可.
【解答】解:设平移后点P、Q的对应点分别是P′、Q′.
∵P′在x轴上,Q′在y轴上,
则P′纵坐标为0,Q′横坐标为0,
∵0﹣m=﹣m,
∴m﹣4﹣m=﹣4,
∴点P平移后的对应点的坐标是(﹣4,0);
故选:A.
4.下列图形中,不能通过其中一个图形平移得到的是( )
A. B.
C. D.
【考点】利用平移设计图案.
【答案】A
【分析】根据平移与旋转的性质即可得出结论.
【解答】解:A.不能通过其中一个四边形平移得到,需要一个四边形旋转得到,符合题意;
B.能通过其中一个四边形平移得到,不合题意;
C.能通过其中一个四边形平移得到,不合题意;
D.能通过其中一个四边形平移得到,不合题意.
故选:A.
5.在俄罗斯方块游戏中,已拼好的图案如图所示,现出现一小方格体正向下运动,你必须进行以下( )操作,才能拼成一个完整图案,使所有图案消失.
A.顺时针旋转90°,向右平移
B.逆时针旋转90°,向右平移
C.顺时针旋转90°,向下平移
D.逆时针旋转90°,向下平移
【考点】生活中的旋转现象;生活中的平移现象.
【答案】A
【分析】在俄罗斯方块游戏中,要使其自动消失,要把三行排满,需要旋转和平移,通过观察即可得到.
【解答】解:顺时针旋转90°,向右平移.
故选:A.
6.在平面直角坐标系中,点P(m2+1,2)关于原点对称的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】关于原点对称的点的坐标.
【答案】C
【分析】根据两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的对称点是P′(﹣x,﹣y),进而得出答案.
【解答】解:∵m2≥0,
∴m2+1>0,
∴点P(m2+1,2)在第一象限,
∴点P(m2+1,2)关于原点对称的点在第三象限,
故选:C.
7.如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A. B. C. D.
【考点】中心对称;全等三角形的判定与性质;等边三角形的判定与性质;菱形的性质.
【答案】C
【分析】证明△BEF是等边三角形,求出EF,同法可证△DGH,△EOH,△OFG都是等边三角形,求出EH,GF,FG即可.
【解答】解:如图,连接BD,AC.
∵四边形ABCD是菱形,∠BAD=120°,
∴AB=BC=CD=AD=2,∠BAO=∠DAO=60°,BD⊥AC,
∴∠ABO=∠CBO=30°,
∴OA=AB=1,OB=OA=,
∵OE⊥AB,OF⊥BC,
∴OE=OF,
∵OB=OB,
∴Rt△BEO≌Rt△BFO(HL),
∴BE=BF,
∵∠EBF=60°,
∴△BEF是等边三角形,
∵S△ABO= OA OB= AB OE,
∴1×=2OE,
∴OE=,
Rt△BEO中,∠OBE=30°,
∴OB=2OE=,
∴EF=BE=,
同法可证,△DGH,△OEH,△OFG都是等边三角形,
∴EF=GH=,EH=FG=OE=,
∴四边形EFGH的周长=3+.
故选:C.
8.下面四个图案(忽略旁边一圈的文字):是旋转对称图形的有( )
A.1个 B.2个 C.3个 D.4个
【考点】旋转对称图形.
【答案】C
【分析】根据旋转图形的定义可知.
【解答】解:前三个图形是旋转对称图形;第四个图形不是旋转对称图形.
故选:C.
9.如图,在平面直角坐标系中,画△ABC关于点O成中心对称的图形时,由于紧张对称中心选错,画出的图形是△DEF,请你找出此时的对称中心是( )
A.(2,0) B.(2,1) C.(1,2) D.(1,0)
【考点】作图﹣旋转变换.
【答案】B
【分析】分别求出点A,B,C,D,E,F的坐标,从而可得AD,BE,CF的中点坐标,由此即可得.
【解答】解:由图可知,A(5,2),B(7,6),C(2,4),D(﹣1,0),E(﹣3,﹣4),F(2,﹣2),
∴AD的中点坐标为,即为(2,1),
BE的中点坐标为,即为(2,1),
CF的中点坐标为,即为(2,1),
∴AD,BE,CF的中点坐标均为(2,1),
∴△ABC与△DEF的对称中心是(2,1),
故选:B.
10.如图,将三角尺直立举起靠近墙面,打开手机手电筒照射三角尺,在墙面上形成影子.则三角尺与影子之间属于以下哪种图形变换( )
A.平移 B.轴对称 C.旋转 D.位似
【考点】几何变换的类型.
【答案】D
【分析】根据位似的定义,即可解决问题.
【解答】解:根据位似的定义可知:三角尺与影子之间属于位似.
故选:D.
二.填空题(共10小题)
11.在等边三角形、正方形、菱形、等腰梯形中,是中心对称图形的有 正方形、菱形 .
【考点】中心对称图形.
【答案】见试题解答内容
【分析】根据在同一平面内,如果把一个图形绕某一点旋转180度,旋转后的图形能和原图形完全重合,那么这个图形就叫做中心对称图形,即可解答.
【解答】解:根据中心对称图形的概念,知正方形、菱形都是中心对称图形;
等边三角形和等腰梯形只是轴对称图形.
故答案为:正方形、菱形.
12.已知点P1(a﹣1,1)和P2(2,b﹣1)关于原点对称,则a+b= ﹣1 .
【考点】关于原点对称的点的坐标.
【答案】见试题解答内容
【分析】根据关于原点对称的点的坐标特点可得a﹣1=﹣2,b﹣1=﹣1,再解方程即可得到a、b的值,进而得到答案.
【解答】解:根据题意得:a﹣1=﹣2,b﹣1=﹣1,
解得:a=﹣1,b=0.
则a+b=﹣1.
故答案为:﹣1.
13.如图,将周长为12的△ABC沿BC边向右平移3个单位,得到△DEF,则四边形ABFD的周长为 18 .
【考点】平移的性质.
【答案】18.
【分析】根据平移的性质,对应点的连线AD、CF都等于平移距离,再根据四边形ABFD的周长=△ABC的周长+AD+CF代入数据计算即可得解.
【解答】解:∵△ABC沿BC方向平移2个单位得到△DEF,
∴AD=CF=2,
∴四边形ABFD的周长
=AB+BC+DF+CF+AD
=△ABC的周长+AD+CF
=12+3+3
=18.
故答案为:18.
14.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA、OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E在槽中滑动,若∠BDE=84°,则∠CDE是 68 °.
【考点】旋转的性质;等腰三角形的性质.
【答案】68.
【分析】根据OC=CD=DE,可得∠O=∠ODC,∠DCE=∠DEC,根据三角形的外角性质可知∠DCE=∠O+∠ODC=2∠ODC,进一步根据三角形的外角性质可知∠BDE=3∠ODC=84°,即可求出∠ODC的度数,进而求出∠CDE的度数.
【解答】解:∵OC=CD=DE,
∴∠O=∠ODC,∠DCE=∠DEC,
∴∠DCE=∠O+∠ODC=2∠ODC,
∵∠O+∠OED=3∠ODC=∠BDE=84°,
∴∠ODC=28°,
∵∠CDE+∠ODC=180°﹣∠BDE=96°,
∴∠CDE=96°﹣∠ODC=68°.
枚答案为:68.
15.如图,在直角坐标系中,已知点P0的坐标为(1,0),以O为旋转中心,将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2021的坐标是 (﹣21010,﹣21010) .
【考点】坐标与图形变化﹣旋转;规律型:点的坐标.
【答案】(﹣21010,﹣21010).
【分析】根据各象限点的坐标特征和坐标轴上点的坐标特征,由OP1=得到点P1的坐标为(1,1),由OP2=2得到点P2的坐标为(0,2),同样由OP3=2得点P3的坐标为(﹣2,2),由OP4=4,则点P4的坐标为(﹣4,0),由OP5=4得到点P5的坐标为(﹣4,﹣4),每8个点一循环,由于2021=252×8+5,则点P2021的坐标为在与点P4一样,在第三象限上,然后利用OP2021=21010 ,可得点P2021的坐标.
【解答】解:∵OP0=1,
∴P0的坐标为(1,0).
∴OP1=,
∴P1的坐标为(1,1).
同理:OP2=2,
P2的坐标为(0,2).
OP3=2,
P3的坐标为(﹣2,2).
OP4=4,
P4的坐标为(﹣4,0).
OP5=4,
点P5的坐标为(﹣4,﹣4),
而2021=252×8+5,
所以点P2021的坐标在与点P5一样在的第三象限,
而OP2021=21010 ,
所以点P2021的坐标为(﹣21010,﹣21010).
故答案为:(﹣21010,﹣21010).
16.在方格纸中,选择标有序号的一个小正方形涂黑,与图中阴影部分构成中心对称图形.涂黑的小正方形的序号可以为 ①④ .
【考点】利用旋转设计图案.
【答案】①④.
【分析】直接利用中心对称图形的定义分析得出答案.
【解答】解:如图所示:图中阴影部分构成中心对称图形是①④,
故答案为:①④.
17.如图,将△ABP放在每个小正方形的边长为1的网格中,点A、B、P均落在格点上.
(1)△ABP的面积等于 2 ;
(2)若线段AB水平移动到A′B′,且使PA′+PB′最短,请你在如图所示的网格中,用直尺画出A′B′,并简要说明画图的方法(不要求证明) .
【考点】作图﹣平移变换;轴对称﹣最短路线问题.
【答案】见试题解答内容
【分析】(1)直接根据三角形的面积公式即可得出结论;
(2)将点A向下平移2格得到点Q,连接PQ,与点A所在的水平线交于点A′,同时将点PQ向上平移1格,再向右平移2格得到点M、N,连接MN与点B所在水平线交于点B′,连接A′B′即为所求.
【解答】解:(1)S△ABC=×2×2=2.
故答案为:2;
(2)如图所示,A′B′=AB==.
易证△PBB′≌△HAA′,可得PB′=HA′,
∴PA′+PB′=PA′+A′H=PH,
∴当H、A′、P共线时,PA′+PB′的值最小,最小值=PH==
故答案为:.
18.用10根木条组成如图(1)所示的图案,请平移3根木条变成如图(2)所示的图案,这3根木条是 ②④⑥或①⑧⑩ (填写序号即可).
【考点】利用平移设计图案;规律型:图形的变化类.
【答案】②④⑥或①⑧⑩.
【分析】依据平移前后的两个图形的区别,平移3根木条即可变成如图(2)所示的图案.
【解答】解:如图(2)所示:
故答案为:②④⑥或①⑧⑩.
19.八个边长为的正方形如图摆放在平面直角坐标系中,经过p点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为 y=x+ .
【考点】中心对称;一次函数图象上点的坐标特征;待定系数法求一次函数解析式;正方形的性质.
【答案】y=x+.
【分析】过P作PB⊥OB于B,过P作PC⊥OC于C,易知OB=3,利用三角形的面积公式和已知条件求出点A的坐标,根据待定系数法即可得到该直线l的解析式.
【解答】解:如图,过P作PB⊥OB于B,过P作PC⊥OC于C,
∵正方形的边长为,
∴OB=3,
∵经过P点的一条直线l将这八个正方形分成面积相等的两部分,
∴三角形ABP面积是8×()2÷2+()2=10,
∴BP AB=10,即×4 AB=10,
∴AB=,
∴OA=3﹣=,
由此可知直线l经过(0,),(4,3).
设直线l的解析式为y=kx+b,
则,解得.
∴直线l解析式为y=x+.
故答案为:y=x+.
20.如图,在平面直角坐标系中,OA=2,将线段OA绕点O进行旋转,B(2,0),取AB中点C,E(4,0),连接CE,已知点D的坐标为(﹣1,1),那么将线段OA绕点O的旋转过程中,AD+2CE的最小值为 5 .
【考点】几何变换综合题.
【答案】5.
【分析】由则AD+2CE=2(CE+CF)≥2EF,即可求解.
【解答】解:连接BD,取BD中点F,连接CF,则CF=AD,
即AD=2CF,
则AD+2CE=2(CE+CF)≥2EF,
当E、F、C共线时,上式取等号,
∵B(2,0),D(﹣1,1),
则点F(,),
而点E(4,0),
由点E、F的坐标得,EF==,
故AD+2CE的最小值为5.
故答案为:5.
三.解答题(共7小题)
21.如图,△ABC沿直线l向右平移4cm,得到△FDE,且BC=6cm,∠ABC=45°.
(1)求BE的长.
(2)求∠FDB的度数.
【考点】平移的性质.
【答案】(1)10cm;
(2)135°.
【分析】(1)根据平移的性质:平移前后的两个图形的对应线段平行且相等,即可得到结论;
(2)根据平移的性质:对应角相等得到答案即可.
【解答】解:(1)由平移知,BD=CE=4.
∵BC=6,
∴BE=BC+CE=6+4=10(cm).
(2)由平移知,∠FDE=∠ABC=45°,
∴∠FDB=180°﹣∠FDE=135°.
22.如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别为A(﹣2,3),B(﹣3,1),C(0,﹣2).
(1)将△ABC向右平移4个单位后得到△A1B1C1,请画出△A1B1C1;
(2)请直接写出△ABC的面积;
(3)定义:在平面直角坐标系中,横坐标与纵坐标都是整数的点称为“整点”,请直接写出△A1B1C1内部所有的整点的坐标.
【考点】坐标与图形变化﹣平移.
【答案】见试题解答内容
【分析】(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)直接利用将△ABC分割成两个三角形进而得出答案;
(3)直接利用所画图形得出符合题意的点.
【解答】解:(1)如图所示:△A1B1C1即为所求;
(2)S△ABC=×3×1+×3×2=4.5;
(3)A1B1C1内部所有的整点的坐标为:(2,2),(2,1),(3,0).
23.某宾馆重新装修后,考虑在大厅的主楼梯上铺设地毯.已知主楼梯宽3m,其剖面如图所示,若每平方米地毯售价10元,请你计算一下,仅此楼梯,购买地毯需要多少元?
【考点】生活中的平移现象.
【答案】138元.
【分析】根据题意,结合图形,先把楼梯的横竖向上向左平移,构成一个矩形,再求得其面积,则购买地毯的钱数可求.
【解答】解:由题意得:地摊的长为:2.2+2.4=4.6(m),
地摊的面积=4.6×3=13.8(m2).
购买地毯需要10×13.8=138(元).
答:购买地毯需要138元.
24.如图,矩形ABCD绕点C顺时针旋转90°后得到矩形FECG,连接DG交EF于点H,连接AF交DG于点M.求证:AM=FM.
【考点】旋转的性质;全等三角形的判定与性质;矩形的性质.
【答案】见试题解答内容
【分析】由旋转性质可知:AD=FG,DC=CG,可得∠DGC=45°,得出HF=FG=AD,所以可证△ADM≌△FHM(AAS),结论可得.
【解答】证明:由旋转性质可得CD=CG,AD=FG,∠DCG=90°,
∴∠DGC=45°.
∴∠DGF=45°.
∵∠EFG=90°,
∴HF=FG=AD.
∵四边形ABCD与四边形FECG为矩形,
∴AD∥EF.
∴∠DAM=∠HFM.
又∠DMA=∠HMF,
∴△ADM≌△FHM(AAS).
∴AM=FM.
25.如图,在直角坐标系内,已知点A(﹣1,0).
(1)图中点B的坐标是 (﹣3,4) ;
(2)点B关于原点对称的点D的坐标是 (3,﹣4) ;点A关于y轴对称的点C的坐标是 (1,0) ;
(3)在y轴上找一点F,使S△ACF=S△ABC.那么点F的坐标为 (0,﹣4)或(0,4) .
【考点】关于原点对称的点的坐标;三角形的面积;关于x轴、y轴对称的点的坐标.
【答案】(1)(﹣3,4);
(2)(3,﹣4),(1,0);
(3)(0,﹣4)或(0,4).
【分析】(1)根据坐标的意义即可得出点B的坐标;
(2)根据关于原点对称的两个点坐标之间的关系可得出点B关于原点对称的点D的坐标,同理根据关于y轴对称的两个点坐标之间的关系得出点A关于y对称点C的坐标;
(3)根据等底等高的三角形的面积相等求解即可.
【解答】解:(1)过点B作x轴的垂线,垂足所对应的数为﹣3,因此点B的横坐标为﹣3,
过点B作y轴的垂线,垂足所对应的数为4,因此点B的纵坐标为4,
所以点B(﹣3,4);
故答案为:(﹣3,4);
(2)由于关于原点对称的两个点坐标纵横坐标均为互为相反数,
所以点B(﹣3,4)关于原点对称点C(3,﹣4),
由于关于y轴对称的两个点,其横坐标互为相反数,其纵坐标不变,
所以点A(﹣1,0)关于y轴对称点D(1,0),
故答案为:(3,﹣4),(1,0);
(3)设点F的坐标为(0,y),
因为S△ABC==4,S△ACF=S△ABC,
所以|OF|=4,
∴|OF|=4,
解得y=﹣4或4,
∴F的坐标为(0,﹣4)或(0,4).
故答案为:(0,﹣4)或(0,4).
26.如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)画出△ABC关于点O的中心对称图形△A1B1C1;
(2)将△ABC绕坐标原点O逆时针旋转90°,得到△A2B2C2.画出图形,并直接写出点A2、B2、C2的坐标.
【考点】作图﹣旋转变换.
【答案】(1)△A1B1C1即为所求;图形请看解答;
(2)△A2B2C2即为所求,图形请看解答;点A2、B2、C2的坐标分别为:(﹣3,﹣2),(0,﹣6),(0,﹣1).
【分析】(1)根据中心对称的性质即可画出△ABC关于点O的中心对称图形△A1B1C1;
(2)根据旋转的性质即可将△ABC绕坐标原点O逆时针旋转90°,得到△A2B2C2.进而可以写出点A2、B2、C2的坐标.
【解答】解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求,
点A2、B2、C2的坐标分别为:(﹣3,﹣2),(0,﹣6),(0,﹣1).
27.如图,在△ABC中,AB=AC,∠BAC=90°,过点A作BC的垂线AD,垂足为点D.点E为线段DC上一动点(不与点C重合),连接AE,以点A为中心,将线段AE逆时针旋转90°得到线段AF,连接BF,与线段AD交于点G,连接CF.
(1)依题意补全图形;直接写出BC与CF的位置关系;
(2)求证:;
(3)直接写出AE,BE,AG之间的数量关系.
【考点】几何变换综合题.
【答案】(1)补全图形见解析;BC⊥CF;
(2)见解析;
(3)2AE2=4AG2+BE2.
【分析】(1)根据题目中要求补全图形即可;根据将线段AE逆时针旋转90°得到线段AF,得出AE=AF,∠EAF=90°,可证△BAE≌△CAF(SAS),得出∠ABE=∠ACF=45°,可得∠ECF=∠ACB+∠ACF=45°+45°=90°即可;
(2)在AD上取DH=DE,连接BH,证明,得出BE=2DG,证明△BDH≌△ADE(SAS),得出BH=AE,∠DBH=∠DAE,证明△BGH≌△FGA,得出AG=GH,证明DG=GH+DH=AG+DE,即可证明结论;
(3)延长BA交CF延长线于H,根据等腰三角形性质可得AD平分∠BAC,可得,可证△BAG∽△BHF,得出HF=2AG,再证△AEC≌△AFH(AAS),得出EC=FH=2AG,利用勾股定理得出EF2=AE2+AF2=2AE2,EF2=EC2+CF2即2AE2=4AG2+BE2即可.
【解答】解:(1)根据题目要求补全图形,如图所示:
∵将线段AE逆时针旋转90°得到线段AF,
∴AE=AF,∠EAF=90°,
∴∠EAC+∠CAF=90°,
∵AB=AC,∠BAC=90°,
∴∠BAE+∠EAC=90°,∠ABC=∠ACB=45°,
∴∠BAE=∠CAF,
在△BAE和△CAF中,
,
∴△BAE≌△CAF(SAS),
∴∠ABE=∠ACF=45°,
∴∠ECF=∠ACB+∠ACF=45°+45°=90°,
∴BC⊥CF;
(2)证明:在AD上取DH=DE,连接BH,如图所示:
∵AD⊥BC,BC⊥CF,
∴AD∥CF,
∴∠BDG=∠BCF=90°,∠BGD=∠BFC,
∴△BDG∽△BCF,
∴,
∵AB=AC,AD⊥BC,∠BAC=90°,
∴,
∴,
∴,
∴,
∴BG=GF,
∵BD=DC,
∴,
∵△BAE≌△CAF,
∴BE=CF,
∴BE=2DG,
∵BD=AD,∠BDH=∠ADE=90°,DH=DE,
∴△BDH≌△ADE(SAS),
∴BH=AE,∠DBH=∠DAE,
∵AE=AF,
∴BH=AF,
∵∠GAF=∠DAE+∠EAF=∠DAE+90°,∠BHG=∠DBH+∠BDH=∠DBH+90°,
∴∠BHG=∠GAF,
∵∠BGH=∠AGF,
∴△BGH≌△FGA(SAS),
∴AG=GH,
∴DG=GH+DH=AG+DE,
∴;
(3)2AE2=4AG2+BE2.延长BA交CF延长线于H,如图所示:
∵AD⊥BC,AB=AC,
∴AD平分∠BAC,
∴,
∵BG=GF,AG∥HF,
∴∠BAG=∠H=45°,∠AGB=∠HFB,
∴△BAG∽△BHF,
∴,
∴HF=2AG,
∵∠ACE=45°,
∴∠ACE=∠H,
∵∠EAC+∠CAF=90°,∠CAF+∠FAH=90°,
∴∠EAC=∠FAH,
在△AEC和△AFH中,
,
∴△AEC≌△AFH(AAS),
∴EC=FH=2AG,
在Rt△AEF中,根据勾股定理EF2=AE2+AF2=2AE2,
在Rt△ECF中,EF2=EC2+CF2,
即2AE2=4AG2+BE2.
一.选择题(共10小题)
1.中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )
A.中国探火CMEP B.中国探月CLEP
C.中国行星探测MARS D.中国火箭CHINAROCKET
2.下列运动属于平移的是( )
A.急刹车时汽车在地面上的滑动
B.冷水加热时小气泡上升变为大气泡
C.电风扇工作时扇叶的转动
D.在百米比赛中,运动员在赛道上的运动
3.第一象限内有两点P(m﹣4,n),Q(m,n﹣2),将线段PQ平移,使平移后的点P、Q分别在x轴与y轴上,则点P平移后的对应点的坐标是( )
A.(﹣4,0) B.(4,0) C.(0,2) D.(0,﹣2)
4.下列图形中,不能通过其中一个图形平移得到的是( )
A. B.
C. D.
5.在俄罗斯方块游戏中,已拼好的图案如图所示,现出现一小方格体正向下运动,你必须进行以下( )操作,才能拼成一个完整图案,使所有图案消失.
A.顺时针旋转90°,向右平移
B.逆时针旋转90°,向右平移
C.顺时针旋转90°,向下平移
D.逆时针旋转90°,向下平移
6.在平面直角坐标系中,点P(m2+1,2)关于原点对称的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A. B. C. D.
8.下面四个图案(忽略旁边一圈的文字):是旋转对称图形的有( )
A.1个 B.2个 C.3个 D.4个
9.如图,在平面直角坐标系中,画△ABC关于点O成中心对称的图形时,由于紧张对称中心选错,画出的图形是△DEF,请你找出此时的对称中心是( )
A.(2,0) B.(2,1) C.(1,2) D.(1,0)
10.如图,将三角尺直立举起靠近墙面,打开手机手电筒照射三角尺,在墙面上形成影子.则三角尺与影子之间属于以下哪种图形变换( )
A.平移 B.轴对称 C.旋转 D.位似
二.填空题(共10小题)
11.在等边三角形、正方形、菱形、等腰梯形中,是中心对称图形的有 .
12.已知点P1(a﹣1,1)和P2(2,b﹣1)关于原点对称,则a+b= .
13.如图,将周长为12的△ABC沿BC边向右平移3个单位,得到△DEF,则四边形ABFD的周长为 .
14.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA、OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E在槽中滑动,若∠BDE=84°,则∠CDE是 °.
15.如图,在直角坐标系中,已知点P0的坐标为(1,0),以O为旋转中心,将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2021的坐标是 .
16.在方格纸中,选择标有序号的一个小正方形涂黑,与图中阴影部分构成中心对称图形.涂黑的小正方形的序号可以为 .
17.如图,将△ABP放在每个小正方形的边长为1的网格中,点A、B、P均落在格点上.
(1)△ABP的面积等于 ;
(2)若线段AB水平移动到A′B′,且使PA′+PB′最短,请你在如图所示的网格中,用直尺画出A′B′,并简要说明画图的方法(不要求证明) .
18.用10根木条组成如图(1)所示的图案,请平移3根木条变成如图(2)所示的图案,这3根木条是 (填写序号即可).
19.八个边长为的正方形如图摆放在平面直角坐标系中,经过p点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为 .
20.如图,在平面直角坐标系中,OA=2,将线段OA绕点O进行旋转,B(2,0),取AB中点C,E(4,0),连接CE,已知点D的坐标为(﹣1,1),那么将线段OA绕点O的旋转过程中,AD+2CE的最小值为 .
三.解答题(共7小题)
21.如图,△ABC沿直线l向右平移4cm,得到△FDE,且BC=6cm,∠ABC=45°.
(1)求BE的长.
(2)求∠FDB的度数.
22.如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别为A(﹣2,3),B(﹣3,1),C(0,﹣2).
(1)将△ABC向右平移4个单位后得到△A1B1C1,请画出△A1B1C1;
(2)请直接写出△ABC的面积;
(3)定义:在平面直角坐标系中,横坐标与纵坐标都是整数的点称为“整点”,请直接写出△A1B1C1内部所有的整点的坐标.
23.某宾馆重新装修后,考虑在大厅的主楼梯上铺设地毯.已知主楼梯宽3m,其剖面如图所示,若每平方米地毯售价10元,请你计算一下,仅此楼梯,购买地毯需要多少元?
24.如图,矩形ABCD绕点C顺时针旋转90°后得到矩形FECG,连接DG交EF于点H,连接AF交DG于点M.求证:AM=FM.
25.如图,在直角坐标系内,已知点A(﹣1,0).
(1)图中点B的坐标是 ;
(2)点B关于原点对称的点D的坐标是 ;点A关于y轴对称的点C的坐标是 ;
(3)在y轴上找一点F,使S△ACF=S△ABC.那么点F的坐标为 .
26.如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)画出△ABC关于点O的中心对称图形△A1B1C1;
(2)将△ABC绕坐标原点O逆时针旋转90°,得到△A2B2C2.画出图形,并直接写出点A2、B2、C2的坐标.
27.如图,在△ABC中,AB=AC,∠BAC=90°,过点A作BC的垂线AD,垂足为点D.点E为线段DC上一动点(不与点C重合),连接AE,以点A为中心,将线段AE逆时针旋转90°得到线段AF,连接BF,与线段AD交于点G,连接CF.
(1)依题意补全图形;直接写出BC与CF的位置关系;
(2)求证:;
(3)直接写出AE,BE,AG之间的数量关系.
鲁教五四新版八年级上学期《第4章 图形的平移与旋转》
参考答案与试题解析
一.选择题(共10小题)
1.中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )
A.中国探火CMEP B.中国探月CLEP
C.中国行星探测MARS D.中国火箭CHINAROCKET
【考点】中心对称图形.
【答案】D
【分析】根据中心对称图形的概念判断.把一个图形绕某一点旋转180度,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.
【解答】解:选项A、B、C不都能找到一个点,使图形绕某一点旋转180度后与原来的图形重合,所以不是中心对称图形.
选项D能找到一个点,使图形绕某一点旋转180度后与原来的图形重合,所以是中心对称图形.
故选:D.
2.下列运动属于平移的是( )
A.急刹车时汽车在地面上的滑动
B.冷水加热时小气泡上升变为大气泡
C.电风扇工作时扇叶的转动
D.在百米比赛中,运动员在赛道上的运动
【考点】生活中的平移现象.
【答案】A
【分析】根据平移的性质判断即可.
【解答】解:A、急刹车时汽车在地面上的滑动,属于平移,故A符合题意;
B、冷水加热时小气泡上升变为大气泡,不属于平移,故B不符合题意;
C、电风扇工作时扇叶的转动,属于旋转,故C不符合题意;
D、在百米比赛中,运动员在赛道上的运动,不属于平移,故D不符合题意;
故选:A.
3.第一象限内有两点P(m﹣4,n),Q(m,n﹣2),将线段PQ平移,使平移后的点P、Q分别在x轴与y轴上,则点P平移后的对应点的坐标是( )
A.(﹣4,0) B.(4,0) C.(0,2) D.(0,﹣2)
【考点】坐标与图形变化﹣平移.
【答案】A
【分析】根据平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减解答即可.
【解答】解:设平移后点P、Q的对应点分别是P′、Q′.
∵P′在x轴上,Q′在y轴上,
则P′纵坐标为0,Q′横坐标为0,
∵0﹣m=﹣m,
∴m﹣4﹣m=﹣4,
∴点P平移后的对应点的坐标是(﹣4,0);
故选:A.
4.下列图形中,不能通过其中一个图形平移得到的是( )
A. B.
C. D.
【考点】利用平移设计图案.
【答案】A
【分析】根据平移与旋转的性质即可得出结论.
【解答】解:A.不能通过其中一个四边形平移得到,需要一个四边形旋转得到,符合题意;
B.能通过其中一个四边形平移得到,不合题意;
C.能通过其中一个四边形平移得到,不合题意;
D.能通过其中一个四边形平移得到,不合题意.
故选:A.
5.在俄罗斯方块游戏中,已拼好的图案如图所示,现出现一小方格体正向下运动,你必须进行以下( )操作,才能拼成一个完整图案,使所有图案消失.
A.顺时针旋转90°,向右平移
B.逆时针旋转90°,向右平移
C.顺时针旋转90°,向下平移
D.逆时针旋转90°,向下平移
【考点】生活中的旋转现象;生活中的平移现象.
【答案】A
【分析】在俄罗斯方块游戏中,要使其自动消失,要把三行排满,需要旋转和平移,通过观察即可得到.
【解答】解:顺时针旋转90°,向右平移.
故选:A.
6.在平面直角坐标系中,点P(m2+1,2)关于原点对称的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】关于原点对称的点的坐标.
【答案】C
【分析】根据两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的对称点是P′(﹣x,﹣y),进而得出答案.
【解答】解:∵m2≥0,
∴m2+1>0,
∴点P(m2+1,2)在第一象限,
∴点P(m2+1,2)关于原点对称的点在第三象限,
故选:C.
7.如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A. B. C. D.
【考点】中心对称;全等三角形的判定与性质;等边三角形的判定与性质;菱形的性质.
【答案】C
【分析】证明△BEF是等边三角形,求出EF,同法可证△DGH,△EOH,△OFG都是等边三角形,求出EH,GF,FG即可.
【解答】解:如图,连接BD,AC.
∵四边形ABCD是菱形,∠BAD=120°,
∴AB=BC=CD=AD=2,∠BAO=∠DAO=60°,BD⊥AC,
∴∠ABO=∠CBO=30°,
∴OA=AB=1,OB=OA=,
∵OE⊥AB,OF⊥BC,
∴OE=OF,
∵OB=OB,
∴Rt△BEO≌Rt△BFO(HL),
∴BE=BF,
∵∠EBF=60°,
∴△BEF是等边三角形,
∵S△ABO= OA OB= AB OE,
∴1×=2OE,
∴OE=,
Rt△BEO中,∠OBE=30°,
∴OB=2OE=,
∴EF=BE=,
同法可证,△DGH,△OEH,△OFG都是等边三角形,
∴EF=GH=,EH=FG=OE=,
∴四边形EFGH的周长=3+.
故选:C.
8.下面四个图案(忽略旁边一圈的文字):是旋转对称图形的有( )
A.1个 B.2个 C.3个 D.4个
【考点】旋转对称图形.
【答案】C
【分析】根据旋转图形的定义可知.
【解答】解:前三个图形是旋转对称图形;第四个图形不是旋转对称图形.
故选:C.
9.如图,在平面直角坐标系中,画△ABC关于点O成中心对称的图形时,由于紧张对称中心选错,画出的图形是△DEF,请你找出此时的对称中心是( )
A.(2,0) B.(2,1) C.(1,2) D.(1,0)
【考点】作图﹣旋转变换.
【答案】B
【分析】分别求出点A,B,C,D,E,F的坐标,从而可得AD,BE,CF的中点坐标,由此即可得.
【解答】解:由图可知,A(5,2),B(7,6),C(2,4),D(﹣1,0),E(﹣3,﹣4),F(2,﹣2),
∴AD的中点坐标为,即为(2,1),
BE的中点坐标为,即为(2,1),
CF的中点坐标为,即为(2,1),
∴AD,BE,CF的中点坐标均为(2,1),
∴△ABC与△DEF的对称中心是(2,1),
故选:B.
10.如图,将三角尺直立举起靠近墙面,打开手机手电筒照射三角尺,在墙面上形成影子.则三角尺与影子之间属于以下哪种图形变换( )
A.平移 B.轴对称 C.旋转 D.位似
【考点】几何变换的类型.
【答案】D
【分析】根据位似的定义,即可解决问题.
【解答】解:根据位似的定义可知:三角尺与影子之间属于位似.
故选:D.
二.填空题(共10小题)
11.在等边三角形、正方形、菱形、等腰梯形中,是中心对称图形的有 正方形、菱形 .
【考点】中心对称图形.
【答案】见试题解答内容
【分析】根据在同一平面内,如果把一个图形绕某一点旋转180度,旋转后的图形能和原图形完全重合,那么这个图形就叫做中心对称图形,即可解答.
【解答】解:根据中心对称图形的概念,知正方形、菱形都是中心对称图形;
等边三角形和等腰梯形只是轴对称图形.
故答案为:正方形、菱形.
12.已知点P1(a﹣1,1)和P2(2,b﹣1)关于原点对称,则a+b= ﹣1 .
【考点】关于原点对称的点的坐标.
【答案】见试题解答内容
【分析】根据关于原点对称的点的坐标特点可得a﹣1=﹣2,b﹣1=﹣1,再解方程即可得到a、b的值,进而得到答案.
【解答】解:根据题意得:a﹣1=﹣2,b﹣1=﹣1,
解得:a=﹣1,b=0.
则a+b=﹣1.
故答案为:﹣1.
13.如图,将周长为12的△ABC沿BC边向右平移3个单位,得到△DEF,则四边形ABFD的周长为 18 .
【考点】平移的性质.
【答案】18.
【分析】根据平移的性质,对应点的连线AD、CF都等于平移距离,再根据四边形ABFD的周长=△ABC的周长+AD+CF代入数据计算即可得解.
【解答】解:∵△ABC沿BC方向平移2个单位得到△DEF,
∴AD=CF=2,
∴四边形ABFD的周长
=AB+BC+DF+CF+AD
=△ABC的周长+AD+CF
=12+3+3
=18.
故答案为:18.
14.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA、OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E在槽中滑动,若∠BDE=84°,则∠CDE是 68 °.
【考点】旋转的性质;等腰三角形的性质.
【答案】68.
【分析】根据OC=CD=DE,可得∠O=∠ODC,∠DCE=∠DEC,根据三角形的外角性质可知∠DCE=∠O+∠ODC=2∠ODC,进一步根据三角形的外角性质可知∠BDE=3∠ODC=84°,即可求出∠ODC的度数,进而求出∠CDE的度数.
【解答】解:∵OC=CD=DE,
∴∠O=∠ODC,∠DCE=∠DEC,
∴∠DCE=∠O+∠ODC=2∠ODC,
∵∠O+∠OED=3∠ODC=∠BDE=84°,
∴∠ODC=28°,
∵∠CDE+∠ODC=180°﹣∠BDE=96°,
∴∠CDE=96°﹣∠ODC=68°.
枚答案为:68.
15.如图,在直角坐标系中,已知点P0的坐标为(1,0),以O为旋转中心,将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2021的坐标是 (﹣21010,﹣21010) .
【考点】坐标与图形变化﹣旋转;规律型:点的坐标.
【答案】(﹣21010,﹣21010).
【分析】根据各象限点的坐标特征和坐标轴上点的坐标特征,由OP1=得到点P1的坐标为(1,1),由OP2=2得到点P2的坐标为(0,2),同样由OP3=2得点P3的坐标为(﹣2,2),由OP4=4,则点P4的坐标为(﹣4,0),由OP5=4得到点P5的坐标为(﹣4,﹣4),每8个点一循环,由于2021=252×8+5,则点P2021的坐标为在与点P4一样,在第三象限上,然后利用OP2021=21010 ,可得点P2021的坐标.
【解答】解:∵OP0=1,
∴P0的坐标为(1,0).
∴OP1=,
∴P1的坐标为(1,1).
同理:OP2=2,
P2的坐标为(0,2).
OP3=2,
P3的坐标为(﹣2,2).
OP4=4,
P4的坐标为(﹣4,0).
OP5=4,
点P5的坐标为(﹣4,﹣4),
而2021=252×8+5,
所以点P2021的坐标在与点P5一样在的第三象限,
而OP2021=21010 ,
所以点P2021的坐标为(﹣21010,﹣21010).
故答案为:(﹣21010,﹣21010).
16.在方格纸中,选择标有序号的一个小正方形涂黑,与图中阴影部分构成中心对称图形.涂黑的小正方形的序号可以为 ①④ .
【考点】利用旋转设计图案.
【答案】①④.
【分析】直接利用中心对称图形的定义分析得出答案.
【解答】解:如图所示:图中阴影部分构成中心对称图形是①④,
故答案为:①④.
17.如图,将△ABP放在每个小正方形的边长为1的网格中,点A、B、P均落在格点上.
(1)△ABP的面积等于 2 ;
(2)若线段AB水平移动到A′B′,且使PA′+PB′最短,请你在如图所示的网格中,用直尺画出A′B′,并简要说明画图的方法(不要求证明) .
【考点】作图﹣平移变换;轴对称﹣最短路线问题.
【答案】见试题解答内容
【分析】(1)直接根据三角形的面积公式即可得出结论;
(2)将点A向下平移2格得到点Q,连接PQ,与点A所在的水平线交于点A′,同时将点PQ向上平移1格,再向右平移2格得到点M、N,连接MN与点B所在水平线交于点B′,连接A′B′即为所求.
【解答】解:(1)S△ABC=×2×2=2.
故答案为:2;
(2)如图所示,A′B′=AB==.
易证△PBB′≌△HAA′,可得PB′=HA′,
∴PA′+PB′=PA′+A′H=PH,
∴当H、A′、P共线时,PA′+PB′的值最小,最小值=PH==
故答案为:.
18.用10根木条组成如图(1)所示的图案,请平移3根木条变成如图(2)所示的图案,这3根木条是 ②④⑥或①⑧⑩ (填写序号即可).
【考点】利用平移设计图案;规律型:图形的变化类.
【答案】②④⑥或①⑧⑩.
【分析】依据平移前后的两个图形的区别,平移3根木条即可变成如图(2)所示的图案.
【解答】解:如图(2)所示:
故答案为:②④⑥或①⑧⑩.
19.八个边长为的正方形如图摆放在平面直角坐标系中,经过p点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为 y=x+ .
【考点】中心对称;一次函数图象上点的坐标特征;待定系数法求一次函数解析式;正方形的性质.
【答案】y=x+.
【分析】过P作PB⊥OB于B,过P作PC⊥OC于C,易知OB=3,利用三角形的面积公式和已知条件求出点A的坐标,根据待定系数法即可得到该直线l的解析式.
【解答】解:如图,过P作PB⊥OB于B,过P作PC⊥OC于C,
∵正方形的边长为,
∴OB=3,
∵经过P点的一条直线l将这八个正方形分成面积相等的两部分,
∴三角形ABP面积是8×()2÷2+()2=10,
∴BP AB=10,即×4 AB=10,
∴AB=,
∴OA=3﹣=,
由此可知直线l经过(0,),(4,3).
设直线l的解析式为y=kx+b,
则,解得.
∴直线l解析式为y=x+.
故答案为:y=x+.
20.如图,在平面直角坐标系中,OA=2,将线段OA绕点O进行旋转,B(2,0),取AB中点C,E(4,0),连接CE,已知点D的坐标为(﹣1,1),那么将线段OA绕点O的旋转过程中,AD+2CE的最小值为 5 .
【考点】几何变换综合题.
【答案】5.
【分析】由则AD+2CE=2(CE+CF)≥2EF,即可求解.
【解答】解:连接BD,取BD中点F,连接CF,则CF=AD,
即AD=2CF,
则AD+2CE=2(CE+CF)≥2EF,
当E、F、C共线时,上式取等号,
∵B(2,0),D(﹣1,1),
则点F(,),
而点E(4,0),
由点E、F的坐标得,EF==,
故AD+2CE的最小值为5.
故答案为:5.
三.解答题(共7小题)
21.如图,△ABC沿直线l向右平移4cm,得到△FDE,且BC=6cm,∠ABC=45°.
(1)求BE的长.
(2)求∠FDB的度数.
【考点】平移的性质.
【答案】(1)10cm;
(2)135°.
【分析】(1)根据平移的性质:平移前后的两个图形的对应线段平行且相等,即可得到结论;
(2)根据平移的性质:对应角相等得到答案即可.
【解答】解:(1)由平移知,BD=CE=4.
∵BC=6,
∴BE=BC+CE=6+4=10(cm).
(2)由平移知,∠FDE=∠ABC=45°,
∴∠FDB=180°﹣∠FDE=135°.
22.如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别为A(﹣2,3),B(﹣3,1),C(0,﹣2).
(1)将△ABC向右平移4个单位后得到△A1B1C1,请画出△A1B1C1;
(2)请直接写出△ABC的面积;
(3)定义:在平面直角坐标系中,横坐标与纵坐标都是整数的点称为“整点”,请直接写出△A1B1C1内部所有的整点的坐标.
【考点】坐标与图形变化﹣平移.
【答案】见试题解答内容
【分析】(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)直接利用将△ABC分割成两个三角形进而得出答案;
(3)直接利用所画图形得出符合题意的点.
【解答】解:(1)如图所示:△A1B1C1即为所求;
(2)S△ABC=×3×1+×3×2=4.5;
(3)A1B1C1内部所有的整点的坐标为:(2,2),(2,1),(3,0).
23.某宾馆重新装修后,考虑在大厅的主楼梯上铺设地毯.已知主楼梯宽3m,其剖面如图所示,若每平方米地毯售价10元,请你计算一下,仅此楼梯,购买地毯需要多少元?
【考点】生活中的平移现象.
【答案】138元.
【分析】根据题意,结合图形,先把楼梯的横竖向上向左平移,构成一个矩形,再求得其面积,则购买地毯的钱数可求.
【解答】解:由题意得:地摊的长为:2.2+2.4=4.6(m),
地摊的面积=4.6×3=13.8(m2).
购买地毯需要10×13.8=138(元).
答:购买地毯需要138元.
24.如图,矩形ABCD绕点C顺时针旋转90°后得到矩形FECG,连接DG交EF于点H,连接AF交DG于点M.求证:AM=FM.
【考点】旋转的性质;全等三角形的判定与性质;矩形的性质.
【答案】见试题解答内容
【分析】由旋转性质可知:AD=FG,DC=CG,可得∠DGC=45°,得出HF=FG=AD,所以可证△ADM≌△FHM(AAS),结论可得.
【解答】证明:由旋转性质可得CD=CG,AD=FG,∠DCG=90°,
∴∠DGC=45°.
∴∠DGF=45°.
∵∠EFG=90°,
∴HF=FG=AD.
∵四边形ABCD与四边形FECG为矩形,
∴AD∥EF.
∴∠DAM=∠HFM.
又∠DMA=∠HMF,
∴△ADM≌△FHM(AAS).
∴AM=FM.
25.如图,在直角坐标系内,已知点A(﹣1,0).
(1)图中点B的坐标是 (﹣3,4) ;
(2)点B关于原点对称的点D的坐标是 (3,﹣4) ;点A关于y轴对称的点C的坐标是 (1,0) ;
(3)在y轴上找一点F,使S△ACF=S△ABC.那么点F的坐标为 (0,﹣4)或(0,4) .
【考点】关于原点对称的点的坐标;三角形的面积;关于x轴、y轴对称的点的坐标.
【答案】(1)(﹣3,4);
(2)(3,﹣4),(1,0);
(3)(0,﹣4)或(0,4).
【分析】(1)根据坐标的意义即可得出点B的坐标;
(2)根据关于原点对称的两个点坐标之间的关系可得出点B关于原点对称的点D的坐标,同理根据关于y轴对称的两个点坐标之间的关系得出点A关于y对称点C的坐标;
(3)根据等底等高的三角形的面积相等求解即可.
【解答】解:(1)过点B作x轴的垂线,垂足所对应的数为﹣3,因此点B的横坐标为﹣3,
过点B作y轴的垂线,垂足所对应的数为4,因此点B的纵坐标为4,
所以点B(﹣3,4);
故答案为:(﹣3,4);
(2)由于关于原点对称的两个点坐标纵横坐标均为互为相反数,
所以点B(﹣3,4)关于原点对称点C(3,﹣4),
由于关于y轴对称的两个点,其横坐标互为相反数,其纵坐标不变,
所以点A(﹣1,0)关于y轴对称点D(1,0),
故答案为:(3,﹣4),(1,0);
(3)设点F的坐标为(0,y),
因为S△ABC==4,S△ACF=S△ABC,
所以|OF|=4,
∴|OF|=4,
解得y=﹣4或4,
∴F的坐标为(0,﹣4)或(0,4).
故答案为:(0,﹣4)或(0,4).
26.如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)画出△ABC关于点O的中心对称图形△A1B1C1;
(2)将△ABC绕坐标原点O逆时针旋转90°,得到△A2B2C2.画出图形,并直接写出点A2、B2、C2的坐标.
【考点】作图﹣旋转变换.
【答案】(1)△A1B1C1即为所求;图形请看解答;
(2)△A2B2C2即为所求,图形请看解答;点A2、B2、C2的坐标分别为:(﹣3,﹣2),(0,﹣6),(0,﹣1).
【分析】(1)根据中心对称的性质即可画出△ABC关于点O的中心对称图形△A1B1C1;
(2)根据旋转的性质即可将△ABC绕坐标原点O逆时针旋转90°,得到△A2B2C2.进而可以写出点A2、B2、C2的坐标.
【解答】解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求,
点A2、B2、C2的坐标分别为:(﹣3,﹣2),(0,﹣6),(0,﹣1).
27.如图,在△ABC中,AB=AC,∠BAC=90°,过点A作BC的垂线AD,垂足为点D.点E为线段DC上一动点(不与点C重合),连接AE,以点A为中心,将线段AE逆时针旋转90°得到线段AF,连接BF,与线段AD交于点G,连接CF.
(1)依题意补全图形;直接写出BC与CF的位置关系;
(2)求证:;
(3)直接写出AE,BE,AG之间的数量关系.
【考点】几何变换综合题.
【答案】(1)补全图形见解析;BC⊥CF;
(2)见解析;
(3)2AE2=4AG2+BE2.
【分析】(1)根据题目中要求补全图形即可;根据将线段AE逆时针旋转90°得到线段AF,得出AE=AF,∠EAF=90°,可证△BAE≌△CAF(SAS),得出∠ABE=∠ACF=45°,可得∠ECF=∠ACB+∠ACF=45°+45°=90°即可;
(2)在AD上取DH=DE,连接BH,证明,得出BE=2DG,证明△BDH≌△ADE(SAS),得出BH=AE,∠DBH=∠DAE,证明△BGH≌△FGA,得出AG=GH,证明DG=GH+DH=AG+DE,即可证明结论;
(3)延长BA交CF延长线于H,根据等腰三角形性质可得AD平分∠BAC,可得,可证△BAG∽△BHF,得出HF=2AG,再证△AEC≌△AFH(AAS),得出EC=FH=2AG,利用勾股定理得出EF2=AE2+AF2=2AE2,EF2=EC2+CF2即2AE2=4AG2+BE2即可.
【解答】解:(1)根据题目要求补全图形,如图所示:
∵将线段AE逆时针旋转90°得到线段AF,
∴AE=AF,∠EAF=90°,
∴∠EAC+∠CAF=90°,
∵AB=AC,∠BAC=90°,
∴∠BAE+∠EAC=90°,∠ABC=∠ACB=45°,
∴∠BAE=∠CAF,
在△BAE和△CAF中,
,
∴△BAE≌△CAF(SAS),
∴∠ABE=∠ACF=45°,
∴∠ECF=∠ACB+∠ACF=45°+45°=90°,
∴BC⊥CF;
(2)证明:在AD上取DH=DE,连接BH,如图所示:
∵AD⊥BC,BC⊥CF,
∴AD∥CF,
∴∠BDG=∠BCF=90°,∠BGD=∠BFC,
∴△BDG∽△BCF,
∴,
∵AB=AC,AD⊥BC,∠BAC=90°,
∴,
∴,
∴,
∴,
∴BG=GF,
∵BD=DC,
∴,
∵△BAE≌△CAF,
∴BE=CF,
∴BE=2DG,
∵BD=AD,∠BDH=∠ADE=90°,DH=DE,
∴△BDH≌△ADE(SAS),
∴BH=AE,∠DBH=∠DAE,
∵AE=AF,
∴BH=AF,
∵∠GAF=∠DAE+∠EAF=∠DAE+90°,∠BHG=∠DBH+∠BDH=∠DBH+90°,
∴∠BHG=∠GAF,
∵∠BGH=∠AGF,
∴△BGH≌△FGA(SAS),
∴AG=GH,
∴DG=GH+DH=AG+DE,
∴;
(3)2AE2=4AG2+BE2.延长BA交CF延长线于H,如图所示:
∵AD⊥BC,AB=AC,
∴AD平分∠BAC,
∴,
∵BG=GF,AG∥HF,
∴∠BAG=∠H=45°,∠AGB=∠HFB,
∴△BAG∽△BHF,
∴,
∴HF=2AG,
∵∠ACE=45°,
∴∠ACE=∠H,
∵∠EAC+∠CAF=90°,∠CAF+∠FAH=90°,
∴∠EAC=∠FAH,
在△AEC和△AFH中,
,
∴△AEC≌△AFH(AAS),
∴EC=FH=2AG,
在Rt△AEF中,根据勾股定理EF2=AE2+AF2=2AE2,
在Rt△ECF中,EF2=EC2+CF2,
即2AE2=4AG2+BE2.
