第1章 三角形 单元测试卷(含解析)2023-2024学年鲁教版(五四制) 数学七年级上册
文档属性
| 名称 | 第1章 三角形 单元测试卷(含解析)2023-2024学年鲁教版(五四制) 数学七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 219.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 16:20:31 | ||
图片预览



文档简介
鲁教五四新版七年级上学期《第1章 三角形》
一.选择题(共15小题)
1.如图中三角形的个数是( )
A.1 B.2 C.3 D.4
2.如图,在△ABC中,AB边上的高为( )
A.CG B.BF C.BE D.AD
3.如图,在△ABC中,点D是BC边上的一点,E,F分别是AD,BE的中点,连接CE,CF,若S△CEF=5,则△ABC的面积为( )
A.15 B.20 C.25 D.30
4.如图,生活中都把自行车的几根梁做成三角形的支架,这是利用三角形的( )
A.全等形 B.稳定性 C.灵活性 D.对称性
5.若三角形的三边长分别为3,1+2x,8,则x的取值范围是( )
A.2<x<5 B.3<x<8 C.4<x<7 D.5<x<9
6.如图,是一块三角形木板的残余部分,量得∠A=110°,∠B=30°,这块三角形木板缺少的角是( )
A.30° B.40° C.50° D.60°
7.如图,在△ABC中,点D为AB边上一点,DE∥BC交△ABC的外角∠ACM的平分线于点E.若∠B=43°,∠E=52°,则∠A的度数为( )
A.51° B.61° C.65° D.75°
8.下列关于全等图形的说法:①两个正方形一定是全等图形;②所有半径相等的圆都是全等图形;③所有的长方形都是全等图形;④如果两个图形全等,那么它们的形状和大小一定都相同.其中,正确的是( )
A.①② B.②③④ C.①②④ D.②④
9.如图,△ABC≌△DEC,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.15° B.25° C.35° D.65°
10.如图,∠C=∠D,那么补充下列一个条件后,仍无法判定△ABC≌△BAD的是( )
A.AD=BC B.AC=BD C.∠CAB=∠DBA D.∠ABC=∠BAD
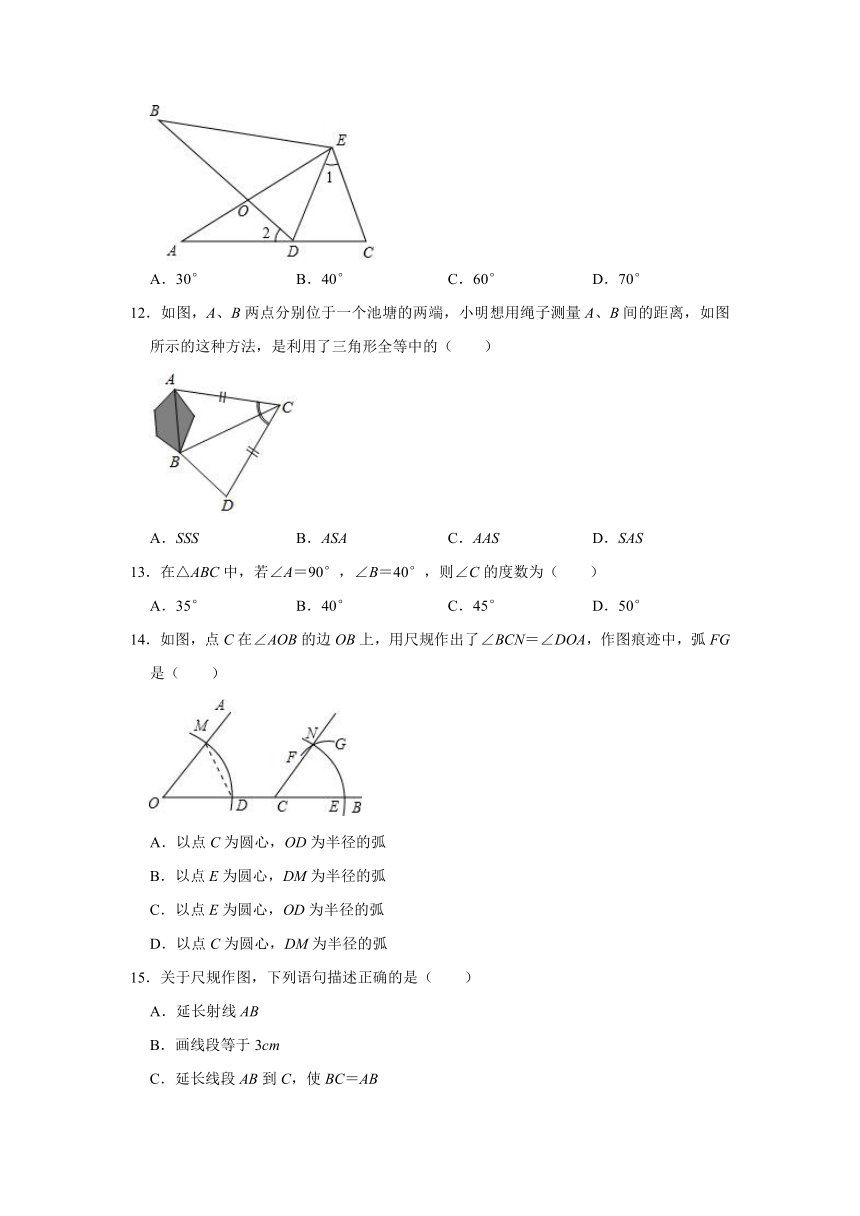
11.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O,若∠1=40°,则∠BDE为( )度.
A.30° B.40° C.60° D.70°
12.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,如图所示的这种方法,是利用了三角形全等中的( )
A.SSS B.ASA C.AAS D.SAS
13.在△ABC中,若∠A=90°,∠B=40°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
14.如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠DOA,作图痕迹中,弧FG是( )
A.以点C为圆心,OD为半径的弧
B.以点E为圆心,DM为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点C为圆心,DM为半径的弧
15.关于尺规作图,下列语句描述正确的是( )
A.延长射线AB
B.画线段等于3cm
C.延长线段AB到C,使BC=AB
D.画线段AB等于直线CD
二.填空题(共10小题)
16.如图,AB是△ACE的 边上的高,在△AEC中,CD是 边上的高,CD还是△ 的高,EF是△ 边上的高.
17.如图,在四边形ABCD中,连接AC和BD,若AC=BC,BD=2AD,∠DAC=∠DBC=45°,△ADC的面积为30,则BD= .
18.中国古建筑很多的房顶横截面是三角形,这是利用了三角形具有 .
19.如图,在△ABC中,AN=2CN,M是AB的中点,BN、CM相交于O,设△BOM的面积为S1,△CON的面积为S2,若△ABC的面积为12,则S1﹣S2= .
20.一个三角形的两边长分别是3和7,最长边a为偶数,则这个三角形的周长为 .
21.已知在△ABC中,∠A=80°,BD,CD分别平分∠ABC和∠ACB,则∠BDC的度数为 .
22.如图,△ABC中,∠A=x°,∠B=37°,外角∠ACD=118°,则x= 度.
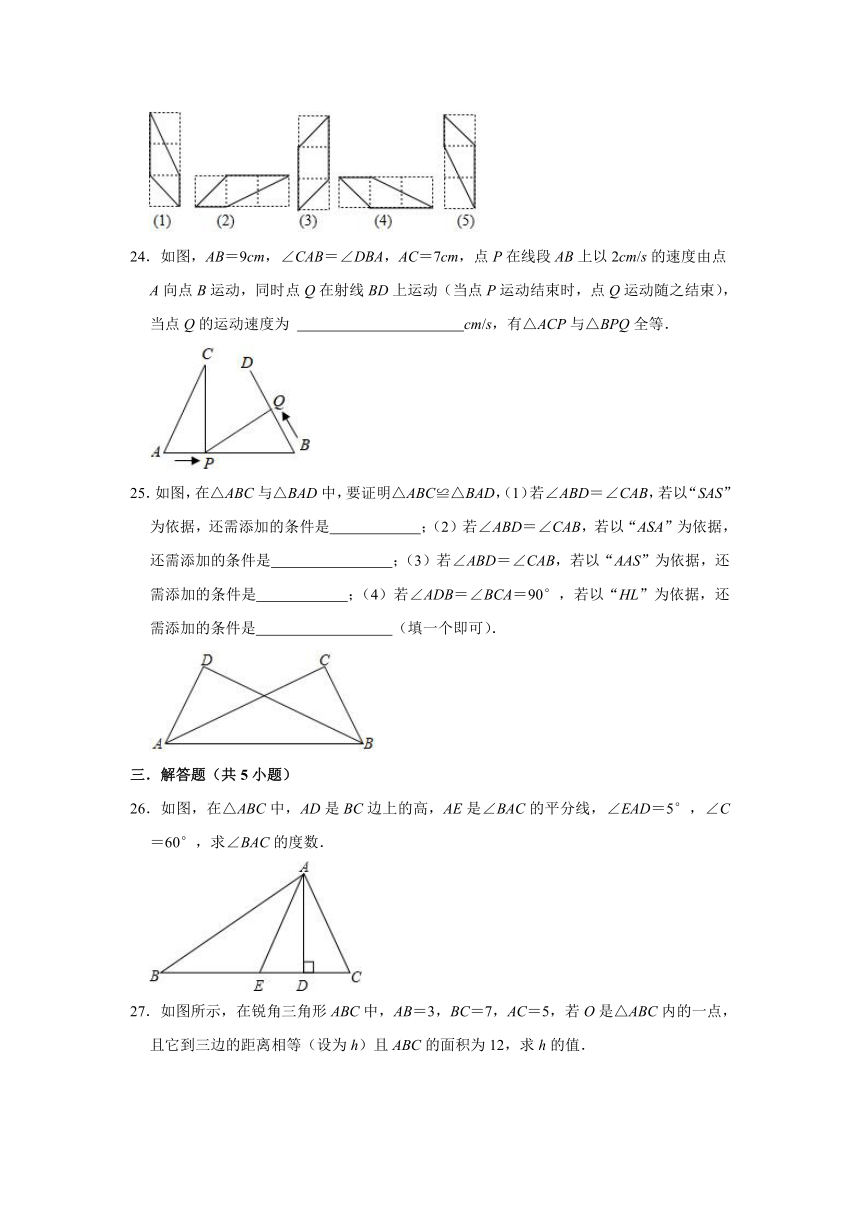
23.如图中有(1)~(5)5个条形方格图,每个小方格的边长均为1,图中(2)~(5)由实线围成的图形与(1)全等的有 .(只填序号即可)
24.如图,AB=9cm,∠CAB=∠DBA,AC=7cm,点P在线段AB上以2cm/s的速度由点A向点B运动,同时点Q在射线BD上运动(当点P运动结束时,点Q运动随之结束),当点Q的运动速度为 cm/s,有△ACP与△BPQ全等.
25.如图,在△ABC与△BAD中,要证明△ABC≌△BAD,(1)若∠ABD=∠CAB,若以“SAS”为依据,还需添加的条件是 ;(2)若∠ABD=∠CAB,若以“ASA”为依据,还需添加的条件是 ;(3)若∠ABD=∠CAB,若以“AAS”为依据,还需添加的条件是 ;(4)若∠ADB=∠BCA=90°,若以“HL”为依据,还需添加的条件是 (填一个即可).
三.解答题(共5小题)
26.如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠C=60°,求∠BAC的度数.
27.如图所示,在锐角三角形ABC中,AB=3,BC=7,AC=5,若O是△ABC内的一点,且它到三边的距离相等(设为h)且ABC的面积为12,求h的值.
28.已知a,b,c是△ABC的三边长.
(1)若a,b,c满足(a﹣b)2+|b﹣c|=0,试判断△ABC的形状;
(2)化简:|b﹣c﹣a|+|a﹣b+c|﹣|a﹣b﹣c|.
29.已知一个三角形的三个内角的度数之比为5:6:7,试判断三角形的形状,并说明理由.
30.在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如图①,若∠A=50°,则∠BPC= ;
(2)如图①,若∠BPC=α,则∠A= ;(用含α的代数式表示)
(3)如图②,作△ABC外角∠MBC、∠NCB的角平分线交于点Q,试探究∠Q与∠BPC之间的数量关系,并说明理由.
鲁教五四新版七年级上学期《第1章 三角形》
参考答案与试题解析
一.选择题(共15小题)
1.如图中三角形的个数是( )
A.1 B.2 C.3 D.4
【考点】三角形.
【答案】C
【分析】图中的三角形有△ABD,△ABC,△BCD,共有3个.
【解答】解:图中的三角形有△ABD,△ABC,△BCD,共有3个.
故选:C.
2.如图,在△ABC中,AB边上的高为( )
A.CG B.BF C.BE D.AD
【考点】三角形的角平分线、中线和高.
【答案】A
【分析】利用三角形高的定义可得答案.
【解答】解:在△ABC中,AB边上的高为CG,
故选:A.
3.如图,在△ABC中,点D是BC边上的一点,E,F分别是AD,BE的中点,连接CE,CF,若S△CEF=5,则△ABC的面积为( )
A.15 B.20 C.25 D.30
【考点】三角形的面积.
【答案】B
【分析】根据三角形的中线把三角形分成面积相等的两个三角形即可求解.
【解答】解:根据等底同高的三角形面积相等,可得
∵F是BE的中点,
S△CFE=S△CFB=5,
∴S△CEB=S△CEF+S△CBF=10,
∵E是AD的中点,
∴S△AEB=S△DBE,S△AEC=S△DEC,
∵S△CEB=S△BDE+S△CDE
∴S△BDE+S△CDE=10
∴S△AEB+S△AEC=10
∴S△ABC=S△BDE+S△CDE+S△AEB+S△AEC=20
故选:B.
4.如图,生活中都把自行车的几根梁做成三角形的支架,这是利用三角形的( )
A.全等形 B.稳定性 C.灵活性 D.对称性
【考点】三角形的稳定性.
【答案】B
【分析】根据三角形具有稳定性解答.
【解答】解:生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有稳定性.
故选:B.
5.若三角形的三边长分别为3,1+2x,8,则x的取值范围是( )
A.2<x<5 B.3<x<8 C.4<x<7 D.5<x<9
【考点】三角形三边关系.
【答案】A
【分析】首先根据三角形的三边关系定理三角形两边之和大于第三边.三角形的两边差小于第三边可得8﹣3<1+2x<3+8,解不等式即可.
【解答】解:根据三角形的三边关系可得:8﹣3<1+2x<3+8,
解得:2<x<5.
故选:A.
6.如图,是一块三角形木板的残余部分,量得∠A=110°,∠B=30°,这块三角形木板缺少的角是( )
A.30° B.40° C.50° D.60°
【考点】三角形内角和定理.
【答案】B
【分析】根据三角形的内角和定理计算即可.
【解答】解:根据三角形的内角和定理第三个角=180°﹣110°﹣30°=40°,
故选:B.
7.如图,在△ABC中,点D为AB边上一点,DE∥BC交△ABC的外角∠ACM的平分线于点E.若∠B=43°,∠E=52°,则∠A的度数为( )
A.51° B.61° C.65° D.75°
【考点】三角形的外角性质;平行线的性质;三角形内角和定理.
【答案】B
【分析】根据DE∥BC,得∠ADE=∠B=43°,再根据三角形内角和定理,得∠A+∠ADE=∠ACE+∠E,由此解答即可.
【解答】解:∵DE∥BC,∠B=43°,
∴∠ADE=∠B=43°,
∵△ABC的外角∠ACM的平分线于点E.
∴∠ACM=∠B+∠A=43°+∠A,
∴∠ACE=,
∵∠A+∠ADE=∠ACE+∠E,
∵,
∴∠A=61°,
故选:B.
8.下列关于全等图形的说法:①两个正方形一定是全等图形;②所有半径相等的圆都是全等图形;③所有的长方形都是全等图形;④如果两个图形全等,那么它们的形状和大小一定都相同.其中,正确的是( )
A.①② B.②③④ C.①②④ D.②④
【考点】全等图形.
【答案】D
【分析】要根据全等形的概念进行判定,与之相符合的是正确的.
【解答】解:①两个正方形不一定是全等图形,说法错误;
②所有半径相等的圆都是全等图形,说法正确;
③所有的长方形不一定都是全等图形,说法错误;
④如果两个图形全等,那么它们的形状和大小一定都相同,说法正确.
故选:D.
9.如图,△ABC≌△DEC,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.15° B.25° C.35° D.65°
【考点】全等三角形的性质.
【答案】B
【分析】根据全等三角形的性质得出∠ACB=∠DCE,求出∠BCE=∠ACD=65°,根据直角三角形的性质得出∠CAF=90°﹣∠ACD,代入求出答案即可.
【解答】解:∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∴∠ACB﹣∠ACE=∠DCE﹣∠ACE,
∴∠BCE=∠ACD,
∵∠BCE=65°,
∴∠ACD=65°,
∵AF⊥CD,
∴∠AFC=90°,
∴∠CAF=90°﹣∠ACD=25°,
故选:B.
10.如图,∠C=∠D,那么补充下列一个条件后,仍无法判定△ABC≌△BAD的是( )
A.AD=BC B.AC=BD C.∠CAB=∠DBA D.∠ABC=∠BAD
【考点】全等三角形的判定.
【答案】A
【分析】根据全等三角形的判定方法即可一一判断.
【解答】解:A、SSA无法判断三角形全等,故本选项符合题意;
B、根据ASA即可判断△ACO≌△BDO,得OC=OD,OA=OB,再用SAS可得三角形全等,故本选项不符合题意;
C、根据AAS即可判断三角形全等,故本选项不符合题意;
D、根据AAS即可判断三角形全等,故本选项不符合题意;
故选:A.
11.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O,若∠1=40°,则∠BDE为( )度.
A.30° B.40° C.60° D.70°
【考点】全等三角形的判定与性质.
【答案】D
【分析】根据全等三角形的判定即可判断△AEC≌△BED,可知:EC=ED,∠C=∠BDE,根据等腰三角形的性质即可知∠C的度数,从而可求出∠BDE的度数.
【解答】解:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,
∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA).
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=40°,
∴∠C=∠EDC=70°,
∴∠BDE=∠C=70°.
故选:D.
12.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,如图所示的这种方法,是利用了三角形全等中的( )
A.SSS B.ASA C.AAS D.SAS
【考点】全等三角形的应用.
【答案】D
【分析】根据题意找到条件,利用全等三角形的判定方法确定正确的选项即可.
【解答】解:观察图形发现:AC=DC,BC=BC,∠ACB=∠DCB,
所以利用了三角形全等中的SAS,
故选:D.
13.在△ABC中,若∠A=90°,∠B=40°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
【考点】直角三角形的性质.
【答案】D
【分析】根据直角三角形的两锐角互余即可得到结论.
【解答】解:∵∠A=90°,
∴∠B+∠C=90°,
∵∠B=40°,
∴∠C=90°﹣40°=50°,
故选:D.
14.如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠DOA,作图痕迹中,弧FG是( )
A.以点C为圆心,OD为半径的弧
B.以点E为圆心,DM为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点C为圆心,DM为半径的弧
【考点】作图—基本作图.
【答案】B
【分析】根据作一个角等于已知角的方法判断即可.
【解答】解:由作图可知,弧FG是以E为圆心,DM为半径的弧.
故选:B.
15.关于尺规作图,下列语句描述正确的是( )
A.延长射线AB
B.画线段等于3cm
C.延长线段AB到C,使BC=AB
D.画线段AB等于直线CD
【考点】作图—复杂作图;直线、射线、线段.
【答案】C
【分析】根据直线、射线、线段的定义对各选项的描述矩形判断.
【解答】解:A.射线向一端无线延伸,所以A选项不符合题意;
B.画线段,使它的长度为3cm,所以B选项不符合题意;
C.延长线段AB到C,使BC=AB,所以C选项符合题意;
D.线段有长度,直线不能度量,所以D选项不符合题意.
故选:C.
二.填空题(共10小题)
16.如图,AB是△ACE的 CE 边上的高,在△AEC中,CD是 AE 边上的高,CD还是△ DCE或△ACD 的高,EF是△ EFC 边上的高.
【考点】三角形的角平分线、中线和高.
【答案】CE,AE,DCE或△ACD,EFC.
【分析】根据三角形中高的定义可得答案.
【解答】解:AB是△ACE的CE边上的高,
在△AEC中,CD是AE边上的高,CD还是△DCE或△ACD的高,EF是△EFC边上的高.
故答案为:CE,AE,DCE或△ACD,EFC.
17.如图,在四边形ABCD中,连接AC和BD,若AC=BC,BD=2AD,∠DAC=∠DBC=45°,△ADC的面积为30,则BD= 4 .
【考点】三角形的面积.
【答案】见试题解答内容
【分析】过D作DE⊥AC于E,DF⊥BC于F,推出△ADE∽△BDF,得到==,根据已知条件推出A,B,C,D四点共圆,根据圆周角定理得到∠ABD=∠ACD,∠BAC=∠BDC,根据等腰三角形的性质得到∠CAB=∠CBA,根据全等三角形的性质得到DF=CE,得到CE=DF=2DE,设AE=DE=x,则CE=DF=2x,AC=3x,根据三角形的面积列方程即可得到结论.
【解答】解:过D作DE⊥AC于E,DF⊥BC于F,
∵∠DAC=∠DBC=45°,
∴△ADE与△BDF是等腰直角三角形,
∴△ADE∽△BDF,
∴==,
∵∠DAC=∠DBC=45°,
∴A,B,C,D四点共圆,
∴∠ABD=∠ACD,∠BAC=∠BDC,
∵AC=BC,
∴∠CAB=∠CBA,
∴∠CBA=∠BDC,
∵∠ABD=∠ABC﹣45°,∠CDF=∠BDC﹣45°,
∴∠ABD=∠CDF,
∴∠CDF=∠DCE,
∵∠DEC=∠CFD=90°,CD=DC,
∴△CDE≌△DCF(AAS),
∴DF=CE,
∴CE=DF=2DE,
设AE=DE=x,则CE=DF=2x,
∴AC=3x,
∵△ADC的面积为30,
∴AC DE=×3x x=30,
∴x=2,
∴DF=2x=4,
∴BD=DF=4.
故答案为:4.
18.中国古建筑很多的房顶横截面是三角形,这是利用了三角形具有 稳定性 .
【考点】三角形的稳定性.
【答案】稳定性.
【分析】根据三角形的稳定性解答即可.
【解答】解:中国古建筑很多的房顶横截面是三角形,这是利用了三角形具有稳定性,
故答案为:稳定性.
19.如图,在△ABC中,AN=2CN,M是AB的中点,BN、CM相交于O,设△BOM的面积为S1,△CON的面积为S2,若△ABC的面积为12,则S1﹣S2= 2 .
【考点】三角形的重心;三角形的面积.
【答案】2.
【分析】由于AN=2CN,△ABC的面积为12,由此可以求出△ABN的面积为8,△BNC的面积为4,然后利用已知条件可以分别用S1、S2表示△CBM 的面积、△ACM的面积,最后利用中点的性质即可求解.
【解答】解:在△ABC中,AN=2CN,△ABC的面积为12,
∴△ABN的面积为8,△BNC的面积为4,
∵△BOM的面积为S1,△CON的面积为S2,
∴四边形AMON的面积8﹣S1,△BOC的面积为4﹣S2,
∵M是AB的中点,
∴△CBM 的面积为=△ACM的面积,
∴S1+4﹣S2=8﹣S1+S2,
∴2S1﹣2S2=8﹣4,
∴2(S1﹣S2)=4,
∴S1﹣S2=2.
故答案为:2.
20.一个三角形的两边长分别是3和7,最长边a为偶数,则这个三角形的周长为 18 .
【考点】三角形三边关系.
【答案】18.
【分析】根据三角形的三边关系,第三边的长一定大于已知的两边的差,而小于两边的和.求得相应范围后,根据最长边a为偶数舍去不合题意的值即可.
【解答】解:∵7﹣3=4,7+3=10,
∴4<a<10.
又∵最长边a为偶数,
∴a=8.
∴周长为7+3+8=18.
故答案为:18.
21.已知在△ABC中,∠A=80°,BD,CD分别平分∠ABC和∠ACB,则∠BDC的度数为 130° .
【考点】三角形内角和定理.
【答案】130°.
【分析】根据三角形的内角和等于180°列式求出∠ABC+∠ACB,再根据角平分线的定义求出∠DBC+∠DCB,然后利用三角形的内角和等于180°列式计算即可得解.
【解答】解:如图,
∵∠A=80°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣80°=100°,
∵BD,CD分别平分∠ABC和∠ACB,
∴∠DBC=∠ABC,∠DCB=∠ACB,
∴∠DBC+∠DCB=(∠ABC+∠ACB)=×100°=50°,
在△BCD中,∠BDC=180°﹣(∠DBC+∠DCB)=180°﹣50°=130°.
故答案为:130°.
22.如图,△ABC中,∠A=x°,∠B=37°,外角∠ACD=118°,则x= 81 度.
【考点】三角形的外角性质.
【答案】81.
【分析】三角形的一个外角等于和它不相邻的两个内角的和,由此即可计算.
【解答】解:∵∠ACD=∠A+∠B,
∴∠A=∠ACD﹣∠B,
∵∠B=37°,∠ACD=118°,
∴∠A=118°﹣37°=81°,
∴x=81.
故答案为:81.
23.如图中有(1)~(5)5个条形方格图,每个小方格的边长均为1,图中(2)~(5)由实线围成的图形与(1)全等的有 (2)(4)(5) .(只填序号即可)
【考点】全等图形.
【答案】(2)(4)(5).
【分析】本题可通过旋转,看后边四个实线图形能和(1)中图形完全重合的便是(1)的全等形.
【解答】解:(2)以右下角顶点为定点顺时针旋转90°后,两个实线图形刚好重合,
(3)中为平行四边形,而①中为梯形,所以不能和(1)中图形完全重合,
(4)可上下反转成(2)的情况,然后旋转可和(1)中图形完全重合,
(5)可旋转180°后可和(1)中图形完全重合,
故答案为(2)(4)(5).
24.如图,AB=9cm,∠CAB=∠DBA,AC=7cm,点P在线段AB上以2cm/s的速度由点A向点B运动,同时点Q在射线BD上运动(当点P运动结束时,点Q运动随之结束),当点Q的运动速度为 2或 cm/s,有△ACP与△BPQ全等.
【考点】全等三角形的性质.
【答案】2或.
【分析】根据全等三角形的性质得出方程解答即可.
【解答】解:①若△ACP≌△BPQ,
则AC=BP,AP=BQ,
可得:7=9﹣2t,2t=xt,
解得:x=2,t=1;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,可得:7=xt,2t=9﹣2t
解得:x=,t=.
综上所述,当△ACP与△BPQ全等时x的值为2或.
故答案为:2或.
25.如图,在△ABC与△BAD中,要证明△ABC≌△BAD,(1)若∠ABD=∠CAB,若以“SAS”为依据,还需添加的条件是 AC=BD ;(2)若∠ABD=∠CAB,若以“ASA”为依据,还需添加的条件是 ∠ABC=∠BAD ;(3)若∠ABD=∠CAB,若以“AAS”为依据,还需添加的条件是 ∠C=∠D ;(4)若∠ADB=∠BCA=90°,若以“HL”为依据,还需添加的条件是 AC=BD或BC=AD (填一个即可).
【考点】全等三角形的判定.
【答案】(1)AC=BD;(2)∠ABC=∠BAD;(3)∠C=∠D;(4)AC=BD或BC=AD.
【分析】本题要判定△ABC≌△BAD,已知∠ABD=∠CAB,AB是公共边,具备了一边、一角对应相等,故添加AC=BD、∠ABC=∠BAD、∠C=∠D,可分别根据SAS、ASA、AAS判定全等.若∠ADB=∠BCA=90°,以“HL”为依据,还需添加的条件是AC=BD或BC=AD.
【解答】解:(1)若以“SAS”为依据,则需添加一个条件是AC=BD;
(2)若以“ASA”为依据,则需添加一个条件是∠ABC=∠BAD;
(3)若以“AAS”为依据,则需添加一个条件是∠C=∠D;
(4)∠ADB=∠BCA=90°,若以“HL”为依据,还需添加的条件是AC=BD或BC=AD.
故答案为:(1)AC=BD;(2)∠ABC=∠BAD;(3)∠C=∠D;(4)AC=BD或BC=AD.
三.解答题(共5小题)
26.如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠C=60°,求∠BAC的度数.
【考点】三角形的角平分线、中线和高.
【答案】∠BAC的度数是70°.
【分析】根据直角三角形两锐角互余求出∠AED,再根据三角形内角和求出∠CAE,然后根据角平分线的定义求出∠BAC即可.
【解答】解:∵AD是BC边上的高,∠EAD=5°,
∴∠AED=85°,
∵∠C=60°,
∴∠CAE=180°﹣∠AED﹣∠C=35°,
∵AE是∠BAC的角平分线,
∴∠BAC=2∠CAE=70°,
答:∠BAC的度数是70°.
27.如图所示,在锐角三角形ABC中,AB=3,BC=7,AC=5,若O是△ABC内的一点,且它到三边的距离相等(设为h)且ABC的面积为12,求h的值.
【考点】三角形的面积.
【答案】.
【分析】根据三角形的面积公式计算即可.
【解答】解:∵AB=3,BC=7,AC=5,
∴S△ABC=S△AOB+S△BOC+S△AOC
=AB h+BC h+AC h
=×3h+×7h+×5h=12,
∴h=.
28.已知a,b,c是△ABC的三边长.
(1)若a,b,c满足(a﹣b)2+|b﹣c|=0,试判断△ABC的形状;
(2)化简:|b﹣c﹣a|+|a﹣b+c|﹣|a﹣b﹣c|.
【考点】三角形三边关系;非负数的性质:绝对值;非负数的性质:偶次方.
【答案】(1)△ABC为等边三角形;
(2)3a﹣3b+c.
【分析】(1)根据非负数的性质,可得出a=b=c,进而得出结论;
(2)利用三角形的三边关系得到b﹣c﹣a<0,a﹣b+c>0,a﹣b﹣c<0,然后去绝对值符号后化简即可.
【解答】解:(1)∵(a﹣b)2+|b﹣c|=0,
∴a﹣b=0且b﹣c=0,
∴a=b=c,
∴△ABC为等边三角形;
(2)∵a,b,c是△ABC的三边长,
∴b﹣c﹣a<0,a﹣b+c>0,a﹣b﹣c<0,
∴原式=﹣b+c+a+a﹣b+c+a﹣b﹣c=3a﹣3b+c.
29.已知一个三角形的三个内角的度数之比为5:6:7,试判断三角形的形状,并说明理由.
【考点】三角形内角和定理.
【答案】锐角三角形,理由详见解答过程.
【分析】运用方程的思想以及三角形内角和定理解决此题.
【解答】解:这个三角形是锐角三角形,理由如下:
根据题意,设这个三角形的三个内角的度数分别为5x、6x、7x.
∴5x+6x+7x=180°,
∴x=10°.
∴5x=50°,6x=60°,7x=70°.
∴这个三角形是锐角三角形.
30.在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如图①,若∠A=50°,则∠BPC= 115° ;
(2)如图①,若∠BPC=α,则∠A= 2α﹣180° ;(用含α的代数式表示)
(3)如图②,作△ABC外角∠MBC、∠NCB的角平分线交于点Q,试探究∠Q与∠BPC之间的数量关系,并说明理由.
【考点】三角形的外角性质;三角形内角和定理.
【答案】(1)115°;
(2)2α﹣180°;
(3)∠P+∠Q=180°,见解答过程.
【分析】(1)运用三角形的内角和定理及角平分线的定义,首先求出∠PBC+∠PCB,进而求出∠P即可解决问题;
(2)结合(1)进行求解即可;
(3)由角平分线的定义可得∠PBC=∠ABC,∠PCB=∠ACB,∠QBC=∠MBC,∠QCB=∠QCB,结合平角的定义可求得∠PBQ=∠PCQ=90°,利用四边形的内角和为360°,可求得∠Q与∠BPC的关系.
【解答】解:(1)在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵∠ABC与∠ACB的平分线相交于点P,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠PBC+∠PCB=(∠ABC+∠ACB)=90°﹣∠A,
∴∠BPC=180°﹣(∠PBC+∠PCB)=90°+∠A,
∵∠A=50°,
∴∠BPC=115°,
故答案为:115°;
(2)在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵∠ABC与∠ACB的平分线相交于点P,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠PBC+∠PCB=(∠ABC+∠ACB)=90°﹣∠A,
∴∠BPC=180°﹣(∠PBC+∠PCB)=90°+∠A,
∵∠BPC=α,
∴α=90°+∠A,
则∠A=2α﹣180°,
故答案为:2α﹣180°;
(3)∠P+∠Q=180°,理由如下:
∵∠ABC与∠ACB的平分线相交于点P,∠MBC、∠NCB的角平分线交于点Q,
∴∠PBC=∠ABC,∠PCB=∠ACB,∠QBC=∠MBC,∠QCB=∠QCB,
∴∠PBC+∠QBC=(∠ABC+∠MBC),
∠PCB+∠QCB=(∠ACB+∠MCB),
∵∠ABC+∠MBC=180°,∠ACB+∠MCB=180°,
∴∠PBQ=∠PCQ=90°,
∴∠P+∠Q=360°﹣∠PBQ﹣∠PCQ=180°.
一.选择题(共15小题)
1.如图中三角形的个数是( )
A.1 B.2 C.3 D.4
2.如图,在△ABC中,AB边上的高为( )
A.CG B.BF C.BE D.AD
3.如图,在△ABC中,点D是BC边上的一点,E,F分别是AD,BE的中点,连接CE,CF,若S△CEF=5,则△ABC的面积为( )
A.15 B.20 C.25 D.30
4.如图,生活中都把自行车的几根梁做成三角形的支架,这是利用三角形的( )
A.全等形 B.稳定性 C.灵活性 D.对称性
5.若三角形的三边长分别为3,1+2x,8,则x的取值范围是( )
A.2<x<5 B.3<x<8 C.4<x<7 D.5<x<9
6.如图,是一块三角形木板的残余部分,量得∠A=110°,∠B=30°,这块三角形木板缺少的角是( )
A.30° B.40° C.50° D.60°
7.如图,在△ABC中,点D为AB边上一点,DE∥BC交△ABC的外角∠ACM的平分线于点E.若∠B=43°,∠E=52°,则∠A的度数为( )
A.51° B.61° C.65° D.75°
8.下列关于全等图形的说法:①两个正方形一定是全等图形;②所有半径相等的圆都是全等图形;③所有的长方形都是全等图形;④如果两个图形全等,那么它们的形状和大小一定都相同.其中,正确的是( )
A.①② B.②③④ C.①②④ D.②④
9.如图,△ABC≌△DEC,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.15° B.25° C.35° D.65°
10.如图,∠C=∠D,那么补充下列一个条件后,仍无法判定△ABC≌△BAD的是( )
A.AD=BC B.AC=BD C.∠CAB=∠DBA D.∠ABC=∠BAD
11.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O,若∠1=40°,则∠BDE为( )度.
A.30° B.40° C.60° D.70°
12.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,如图所示的这种方法,是利用了三角形全等中的( )
A.SSS B.ASA C.AAS D.SAS
13.在△ABC中,若∠A=90°,∠B=40°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
14.如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠DOA,作图痕迹中,弧FG是( )
A.以点C为圆心,OD为半径的弧
B.以点E为圆心,DM为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点C为圆心,DM为半径的弧
15.关于尺规作图,下列语句描述正确的是( )
A.延长射线AB
B.画线段等于3cm
C.延长线段AB到C,使BC=AB
D.画线段AB等于直线CD
二.填空题(共10小题)
16.如图,AB是△ACE的 边上的高,在△AEC中,CD是 边上的高,CD还是△ 的高,EF是△ 边上的高.
17.如图,在四边形ABCD中,连接AC和BD,若AC=BC,BD=2AD,∠DAC=∠DBC=45°,△ADC的面积为30,则BD= .
18.中国古建筑很多的房顶横截面是三角形,这是利用了三角形具有 .
19.如图,在△ABC中,AN=2CN,M是AB的中点,BN、CM相交于O,设△BOM的面积为S1,△CON的面积为S2,若△ABC的面积为12,则S1﹣S2= .
20.一个三角形的两边长分别是3和7,最长边a为偶数,则这个三角形的周长为 .
21.已知在△ABC中,∠A=80°,BD,CD分别平分∠ABC和∠ACB,则∠BDC的度数为 .
22.如图,△ABC中,∠A=x°,∠B=37°,外角∠ACD=118°,则x= 度.
23.如图中有(1)~(5)5个条形方格图,每个小方格的边长均为1,图中(2)~(5)由实线围成的图形与(1)全等的有 .(只填序号即可)
24.如图,AB=9cm,∠CAB=∠DBA,AC=7cm,点P在线段AB上以2cm/s的速度由点A向点B运动,同时点Q在射线BD上运动(当点P运动结束时,点Q运动随之结束),当点Q的运动速度为 cm/s,有△ACP与△BPQ全等.
25.如图,在△ABC与△BAD中,要证明△ABC≌△BAD,(1)若∠ABD=∠CAB,若以“SAS”为依据,还需添加的条件是 ;(2)若∠ABD=∠CAB,若以“ASA”为依据,还需添加的条件是 ;(3)若∠ABD=∠CAB,若以“AAS”为依据,还需添加的条件是 ;(4)若∠ADB=∠BCA=90°,若以“HL”为依据,还需添加的条件是 (填一个即可).
三.解答题(共5小题)
26.如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠C=60°,求∠BAC的度数.
27.如图所示,在锐角三角形ABC中,AB=3,BC=7,AC=5,若O是△ABC内的一点,且它到三边的距离相等(设为h)且ABC的面积为12,求h的值.
28.已知a,b,c是△ABC的三边长.
(1)若a,b,c满足(a﹣b)2+|b﹣c|=0,试判断△ABC的形状;
(2)化简:|b﹣c﹣a|+|a﹣b+c|﹣|a﹣b﹣c|.
29.已知一个三角形的三个内角的度数之比为5:6:7,试判断三角形的形状,并说明理由.
30.在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如图①,若∠A=50°,则∠BPC= ;
(2)如图①,若∠BPC=α,则∠A= ;(用含α的代数式表示)
(3)如图②,作△ABC外角∠MBC、∠NCB的角平分线交于点Q,试探究∠Q与∠BPC之间的数量关系,并说明理由.
鲁教五四新版七年级上学期《第1章 三角形》
参考答案与试题解析
一.选择题(共15小题)
1.如图中三角形的个数是( )
A.1 B.2 C.3 D.4
【考点】三角形.
【答案】C
【分析】图中的三角形有△ABD,△ABC,△BCD,共有3个.
【解答】解:图中的三角形有△ABD,△ABC,△BCD,共有3个.
故选:C.
2.如图,在△ABC中,AB边上的高为( )
A.CG B.BF C.BE D.AD
【考点】三角形的角平分线、中线和高.
【答案】A
【分析】利用三角形高的定义可得答案.
【解答】解:在△ABC中,AB边上的高为CG,
故选:A.
3.如图,在△ABC中,点D是BC边上的一点,E,F分别是AD,BE的中点,连接CE,CF,若S△CEF=5,则△ABC的面积为( )
A.15 B.20 C.25 D.30
【考点】三角形的面积.
【答案】B
【分析】根据三角形的中线把三角形分成面积相等的两个三角形即可求解.
【解答】解:根据等底同高的三角形面积相等,可得
∵F是BE的中点,
S△CFE=S△CFB=5,
∴S△CEB=S△CEF+S△CBF=10,
∵E是AD的中点,
∴S△AEB=S△DBE,S△AEC=S△DEC,
∵S△CEB=S△BDE+S△CDE
∴S△BDE+S△CDE=10
∴S△AEB+S△AEC=10
∴S△ABC=S△BDE+S△CDE+S△AEB+S△AEC=20
故选:B.
4.如图,生活中都把自行车的几根梁做成三角形的支架,这是利用三角形的( )
A.全等形 B.稳定性 C.灵活性 D.对称性
【考点】三角形的稳定性.
【答案】B
【分析】根据三角形具有稳定性解答.
【解答】解:生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有稳定性.
故选:B.
5.若三角形的三边长分别为3,1+2x,8,则x的取值范围是( )
A.2<x<5 B.3<x<8 C.4<x<7 D.5<x<9
【考点】三角形三边关系.
【答案】A
【分析】首先根据三角形的三边关系定理三角形两边之和大于第三边.三角形的两边差小于第三边可得8﹣3<1+2x<3+8,解不等式即可.
【解答】解:根据三角形的三边关系可得:8﹣3<1+2x<3+8,
解得:2<x<5.
故选:A.
6.如图,是一块三角形木板的残余部分,量得∠A=110°,∠B=30°,这块三角形木板缺少的角是( )
A.30° B.40° C.50° D.60°
【考点】三角形内角和定理.
【答案】B
【分析】根据三角形的内角和定理计算即可.
【解答】解:根据三角形的内角和定理第三个角=180°﹣110°﹣30°=40°,
故选:B.
7.如图,在△ABC中,点D为AB边上一点,DE∥BC交△ABC的外角∠ACM的平分线于点E.若∠B=43°,∠E=52°,则∠A的度数为( )
A.51° B.61° C.65° D.75°
【考点】三角形的外角性质;平行线的性质;三角形内角和定理.
【答案】B
【分析】根据DE∥BC,得∠ADE=∠B=43°,再根据三角形内角和定理,得∠A+∠ADE=∠ACE+∠E,由此解答即可.
【解答】解:∵DE∥BC,∠B=43°,
∴∠ADE=∠B=43°,
∵△ABC的外角∠ACM的平分线于点E.
∴∠ACM=∠B+∠A=43°+∠A,
∴∠ACE=,
∵∠A+∠ADE=∠ACE+∠E,
∵,
∴∠A=61°,
故选:B.
8.下列关于全等图形的说法:①两个正方形一定是全等图形;②所有半径相等的圆都是全等图形;③所有的长方形都是全等图形;④如果两个图形全等,那么它们的形状和大小一定都相同.其中,正确的是( )
A.①② B.②③④ C.①②④ D.②④
【考点】全等图形.
【答案】D
【分析】要根据全等形的概念进行判定,与之相符合的是正确的.
【解答】解:①两个正方形不一定是全等图形,说法错误;
②所有半径相等的圆都是全等图形,说法正确;
③所有的长方形不一定都是全等图形,说法错误;
④如果两个图形全等,那么它们的形状和大小一定都相同,说法正确.
故选:D.
9.如图,△ABC≌△DEC,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.15° B.25° C.35° D.65°
【考点】全等三角形的性质.
【答案】B
【分析】根据全等三角形的性质得出∠ACB=∠DCE,求出∠BCE=∠ACD=65°,根据直角三角形的性质得出∠CAF=90°﹣∠ACD,代入求出答案即可.
【解答】解:∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∴∠ACB﹣∠ACE=∠DCE﹣∠ACE,
∴∠BCE=∠ACD,
∵∠BCE=65°,
∴∠ACD=65°,
∵AF⊥CD,
∴∠AFC=90°,
∴∠CAF=90°﹣∠ACD=25°,
故选:B.
10.如图,∠C=∠D,那么补充下列一个条件后,仍无法判定△ABC≌△BAD的是( )
A.AD=BC B.AC=BD C.∠CAB=∠DBA D.∠ABC=∠BAD
【考点】全等三角形的判定.
【答案】A
【分析】根据全等三角形的判定方法即可一一判断.
【解答】解:A、SSA无法判断三角形全等,故本选项符合题意;
B、根据ASA即可判断△ACO≌△BDO,得OC=OD,OA=OB,再用SAS可得三角形全等,故本选项不符合题意;
C、根据AAS即可判断三角形全等,故本选项不符合题意;
D、根据AAS即可判断三角形全等,故本选项不符合题意;
故选:A.
11.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O,若∠1=40°,则∠BDE为( )度.
A.30° B.40° C.60° D.70°
【考点】全等三角形的判定与性质.
【答案】D
【分析】根据全等三角形的判定即可判断△AEC≌△BED,可知:EC=ED,∠C=∠BDE,根据等腰三角形的性质即可知∠C的度数,从而可求出∠BDE的度数.
【解答】解:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,
∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA).
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=40°,
∴∠C=∠EDC=70°,
∴∠BDE=∠C=70°.
故选:D.
12.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,如图所示的这种方法,是利用了三角形全等中的( )
A.SSS B.ASA C.AAS D.SAS
【考点】全等三角形的应用.
【答案】D
【分析】根据题意找到条件,利用全等三角形的判定方法确定正确的选项即可.
【解答】解:观察图形发现:AC=DC,BC=BC,∠ACB=∠DCB,
所以利用了三角形全等中的SAS,
故选:D.
13.在△ABC中,若∠A=90°,∠B=40°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
【考点】直角三角形的性质.
【答案】D
【分析】根据直角三角形的两锐角互余即可得到结论.
【解答】解:∵∠A=90°,
∴∠B+∠C=90°,
∵∠B=40°,
∴∠C=90°﹣40°=50°,
故选:D.
14.如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠DOA,作图痕迹中,弧FG是( )
A.以点C为圆心,OD为半径的弧
B.以点E为圆心,DM为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点C为圆心,DM为半径的弧
【考点】作图—基本作图.
【答案】B
【分析】根据作一个角等于已知角的方法判断即可.
【解答】解:由作图可知,弧FG是以E为圆心,DM为半径的弧.
故选:B.
15.关于尺规作图,下列语句描述正确的是( )
A.延长射线AB
B.画线段等于3cm
C.延长线段AB到C,使BC=AB
D.画线段AB等于直线CD
【考点】作图—复杂作图;直线、射线、线段.
【答案】C
【分析】根据直线、射线、线段的定义对各选项的描述矩形判断.
【解答】解:A.射线向一端无线延伸,所以A选项不符合题意;
B.画线段,使它的长度为3cm,所以B选项不符合题意;
C.延长线段AB到C,使BC=AB,所以C选项符合题意;
D.线段有长度,直线不能度量,所以D选项不符合题意.
故选:C.
二.填空题(共10小题)
16.如图,AB是△ACE的 CE 边上的高,在△AEC中,CD是 AE 边上的高,CD还是△ DCE或△ACD 的高,EF是△ EFC 边上的高.
【考点】三角形的角平分线、中线和高.
【答案】CE,AE,DCE或△ACD,EFC.
【分析】根据三角形中高的定义可得答案.
【解答】解:AB是△ACE的CE边上的高,
在△AEC中,CD是AE边上的高,CD还是△DCE或△ACD的高,EF是△EFC边上的高.
故答案为:CE,AE,DCE或△ACD,EFC.
17.如图,在四边形ABCD中,连接AC和BD,若AC=BC,BD=2AD,∠DAC=∠DBC=45°,△ADC的面积为30,则BD= 4 .
【考点】三角形的面积.
【答案】见试题解答内容
【分析】过D作DE⊥AC于E,DF⊥BC于F,推出△ADE∽△BDF,得到==,根据已知条件推出A,B,C,D四点共圆,根据圆周角定理得到∠ABD=∠ACD,∠BAC=∠BDC,根据等腰三角形的性质得到∠CAB=∠CBA,根据全等三角形的性质得到DF=CE,得到CE=DF=2DE,设AE=DE=x,则CE=DF=2x,AC=3x,根据三角形的面积列方程即可得到结论.
【解答】解:过D作DE⊥AC于E,DF⊥BC于F,
∵∠DAC=∠DBC=45°,
∴△ADE与△BDF是等腰直角三角形,
∴△ADE∽△BDF,
∴==,
∵∠DAC=∠DBC=45°,
∴A,B,C,D四点共圆,
∴∠ABD=∠ACD,∠BAC=∠BDC,
∵AC=BC,
∴∠CAB=∠CBA,
∴∠CBA=∠BDC,
∵∠ABD=∠ABC﹣45°,∠CDF=∠BDC﹣45°,
∴∠ABD=∠CDF,
∴∠CDF=∠DCE,
∵∠DEC=∠CFD=90°,CD=DC,
∴△CDE≌△DCF(AAS),
∴DF=CE,
∴CE=DF=2DE,
设AE=DE=x,则CE=DF=2x,
∴AC=3x,
∵△ADC的面积为30,
∴AC DE=×3x x=30,
∴x=2,
∴DF=2x=4,
∴BD=DF=4.
故答案为:4.
18.中国古建筑很多的房顶横截面是三角形,这是利用了三角形具有 稳定性 .
【考点】三角形的稳定性.
【答案】稳定性.
【分析】根据三角形的稳定性解答即可.
【解答】解:中国古建筑很多的房顶横截面是三角形,这是利用了三角形具有稳定性,
故答案为:稳定性.
19.如图,在△ABC中,AN=2CN,M是AB的中点,BN、CM相交于O,设△BOM的面积为S1,△CON的面积为S2,若△ABC的面积为12,则S1﹣S2= 2 .
【考点】三角形的重心;三角形的面积.
【答案】2.
【分析】由于AN=2CN,△ABC的面积为12,由此可以求出△ABN的面积为8,△BNC的面积为4,然后利用已知条件可以分别用S1、S2表示△CBM 的面积、△ACM的面积,最后利用中点的性质即可求解.
【解答】解:在△ABC中,AN=2CN,△ABC的面积为12,
∴△ABN的面积为8,△BNC的面积为4,
∵△BOM的面积为S1,△CON的面积为S2,
∴四边形AMON的面积8﹣S1,△BOC的面积为4﹣S2,
∵M是AB的中点,
∴△CBM 的面积为=△ACM的面积,
∴S1+4﹣S2=8﹣S1+S2,
∴2S1﹣2S2=8﹣4,
∴2(S1﹣S2)=4,
∴S1﹣S2=2.
故答案为:2.
20.一个三角形的两边长分别是3和7,最长边a为偶数,则这个三角形的周长为 18 .
【考点】三角形三边关系.
【答案】18.
【分析】根据三角形的三边关系,第三边的长一定大于已知的两边的差,而小于两边的和.求得相应范围后,根据最长边a为偶数舍去不合题意的值即可.
【解答】解:∵7﹣3=4,7+3=10,
∴4<a<10.
又∵最长边a为偶数,
∴a=8.
∴周长为7+3+8=18.
故答案为:18.
21.已知在△ABC中,∠A=80°,BD,CD分别平分∠ABC和∠ACB,则∠BDC的度数为 130° .
【考点】三角形内角和定理.
【答案】130°.
【分析】根据三角形的内角和等于180°列式求出∠ABC+∠ACB,再根据角平分线的定义求出∠DBC+∠DCB,然后利用三角形的内角和等于180°列式计算即可得解.
【解答】解:如图,
∵∠A=80°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣80°=100°,
∵BD,CD分别平分∠ABC和∠ACB,
∴∠DBC=∠ABC,∠DCB=∠ACB,
∴∠DBC+∠DCB=(∠ABC+∠ACB)=×100°=50°,
在△BCD中,∠BDC=180°﹣(∠DBC+∠DCB)=180°﹣50°=130°.
故答案为:130°.
22.如图,△ABC中,∠A=x°,∠B=37°,外角∠ACD=118°,则x= 81 度.
【考点】三角形的外角性质.
【答案】81.
【分析】三角形的一个外角等于和它不相邻的两个内角的和,由此即可计算.
【解答】解:∵∠ACD=∠A+∠B,
∴∠A=∠ACD﹣∠B,
∵∠B=37°,∠ACD=118°,
∴∠A=118°﹣37°=81°,
∴x=81.
故答案为:81.
23.如图中有(1)~(5)5个条形方格图,每个小方格的边长均为1,图中(2)~(5)由实线围成的图形与(1)全等的有 (2)(4)(5) .(只填序号即可)
【考点】全等图形.
【答案】(2)(4)(5).
【分析】本题可通过旋转,看后边四个实线图形能和(1)中图形完全重合的便是(1)的全等形.
【解答】解:(2)以右下角顶点为定点顺时针旋转90°后,两个实线图形刚好重合,
(3)中为平行四边形,而①中为梯形,所以不能和(1)中图形完全重合,
(4)可上下反转成(2)的情况,然后旋转可和(1)中图形完全重合,
(5)可旋转180°后可和(1)中图形完全重合,
故答案为(2)(4)(5).
24.如图,AB=9cm,∠CAB=∠DBA,AC=7cm,点P在线段AB上以2cm/s的速度由点A向点B运动,同时点Q在射线BD上运动(当点P运动结束时,点Q运动随之结束),当点Q的运动速度为 2或 cm/s,有△ACP与△BPQ全等.
【考点】全等三角形的性质.
【答案】2或.
【分析】根据全等三角形的性质得出方程解答即可.
【解答】解:①若△ACP≌△BPQ,
则AC=BP,AP=BQ,
可得:7=9﹣2t,2t=xt,
解得:x=2,t=1;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,可得:7=xt,2t=9﹣2t
解得:x=,t=.
综上所述,当△ACP与△BPQ全等时x的值为2或.
故答案为:2或.
25.如图,在△ABC与△BAD中,要证明△ABC≌△BAD,(1)若∠ABD=∠CAB,若以“SAS”为依据,还需添加的条件是 AC=BD ;(2)若∠ABD=∠CAB,若以“ASA”为依据,还需添加的条件是 ∠ABC=∠BAD ;(3)若∠ABD=∠CAB,若以“AAS”为依据,还需添加的条件是 ∠C=∠D ;(4)若∠ADB=∠BCA=90°,若以“HL”为依据,还需添加的条件是 AC=BD或BC=AD (填一个即可).
【考点】全等三角形的判定.
【答案】(1)AC=BD;(2)∠ABC=∠BAD;(3)∠C=∠D;(4)AC=BD或BC=AD.
【分析】本题要判定△ABC≌△BAD,已知∠ABD=∠CAB,AB是公共边,具备了一边、一角对应相等,故添加AC=BD、∠ABC=∠BAD、∠C=∠D,可分别根据SAS、ASA、AAS判定全等.若∠ADB=∠BCA=90°,以“HL”为依据,还需添加的条件是AC=BD或BC=AD.
【解答】解:(1)若以“SAS”为依据,则需添加一个条件是AC=BD;
(2)若以“ASA”为依据,则需添加一个条件是∠ABC=∠BAD;
(3)若以“AAS”为依据,则需添加一个条件是∠C=∠D;
(4)∠ADB=∠BCA=90°,若以“HL”为依据,还需添加的条件是AC=BD或BC=AD.
故答案为:(1)AC=BD;(2)∠ABC=∠BAD;(3)∠C=∠D;(4)AC=BD或BC=AD.
三.解答题(共5小题)
26.如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠C=60°,求∠BAC的度数.
【考点】三角形的角平分线、中线和高.
【答案】∠BAC的度数是70°.
【分析】根据直角三角形两锐角互余求出∠AED,再根据三角形内角和求出∠CAE,然后根据角平分线的定义求出∠BAC即可.
【解答】解:∵AD是BC边上的高,∠EAD=5°,
∴∠AED=85°,
∵∠C=60°,
∴∠CAE=180°﹣∠AED﹣∠C=35°,
∵AE是∠BAC的角平分线,
∴∠BAC=2∠CAE=70°,
答:∠BAC的度数是70°.
27.如图所示,在锐角三角形ABC中,AB=3,BC=7,AC=5,若O是△ABC内的一点,且它到三边的距离相等(设为h)且ABC的面积为12,求h的值.
【考点】三角形的面积.
【答案】.
【分析】根据三角形的面积公式计算即可.
【解答】解:∵AB=3,BC=7,AC=5,
∴S△ABC=S△AOB+S△BOC+S△AOC
=AB h+BC h+AC h
=×3h+×7h+×5h=12,
∴h=.
28.已知a,b,c是△ABC的三边长.
(1)若a,b,c满足(a﹣b)2+|b﹣c|=0,试判断△ABC的形状;
(2)化简:|b﹣c﹣a|+|a﹣b+c|﹣|a﹣b﹣c|.
【考点】三角形三边关系;非负数的性质:绝对值;非负数的性质:偶次方.
【答案】(1)△ABC为等边三角形;
(2)3a﹣3b+c.
【分析】(1)根据非负数的性质,可得出a=b=c,进而得出结论;
(2)利用三角形的三边关系得到b﹣c﹣a<0,a﹣b+c>0,a﹣b﹣c<0,然后去绝对值符号后化简即可.
【解答】解:(1)∵(a﹣b)2+|b﹣c|=0,
∴a﹣b=0且b﹣c=0,
∴a=b=c,
∴△ABC为等边三角形;
(2)∵a,b,c是△ABC的三边长,
∴b﹣c﹣a<0,a﹣b+c>0,a﹣b﹣c<0,
∴原式=﹣b+c+a+a﹣b+c+a﹣b﹣c=3a﹣3b+c.
29.已知一个三角形的三个内角的度数之比为5:6:7,试判断三角形的形状,并说明理由.
【考点】三角形内角和定理.
【答案】锐角三角形,理由详见解答过程.
【分析】运用方程的思想以及三角形内角和定理解决此题.
【解答】解:这个三角形是锐角三角形,理由如下:
根据题意,设这个三角形的三个内角的度数分别为5x、6x、7x.
∴5x+6x+7x=180°,
∴x=10°.
∴5x=50°,6x=60°,7x=70°.
∴这个三角形是锐角三角形.
30.在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如图①,若∠A=50°,则∠BPC= 115° ;
(2)如图①,若∠BPC=α,则∠A= 2α﹣180° ;(用含α的代数式表示)
(3)如图②,作△ABC外角∠MBC、∠NCB的角平分线交于点Q,试探究∠Q与∠BPC之间的数量关系,并说明理由.
【考点】三角形的外角性质;三角形内角和定理.
【答案】(1)115°;
(2)2α﹣180°;
(3)∠P+∠Q=180°,见解答过程.
【分析】(1)运用三角形的内角和定理及角平分线的定义,首先求出∠PBC+∠PCB,进而求出∠P即可解决问题;
(2)结合(1)进行求解即可;
(3)由角平分线的定义可得∠PBC=∠ABC,∠PCB=∠ACB,∠QBC=∠MBC,∠QCB=∠QCB,结合平角的定义可求得∠PBQ=∠PCQ=90°,利用四边形的内角和为360°,可求得∠Q与∠BPC的关系.
【解答】解:(1)在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵∠ABC与∠ACB的平分线相交于点P,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠PBC+∠PCB=(∠ABC+∠ACB)=90°﹣∠A,
∴∠BPC=180°﹣(∠PBC+∠PCB)=90°+∠A,
∵∠A=50°,
∴∠BPC=115°,
故答案为:115°;
(2)在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵∠ABC与∠ACB的平分线相交于点P,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠PBC+∠PCB=(∠ABC+∠ACB)=90°﹣∠A,
∴∠BPC=180°﹣(∠PBC+∠PCB)=90°+∠A,
∵∠BPC=α,
∴α=90°+∠A,
则∠A=2α﹣180°,
故答案为:2α﹣180°;
(3)∠P+∠Q=180°,理由如下:
∵∠ABC与∠ACB的平分线相交于点P,∠MBC、∠NCB的角平分线交于点Q,
∴∠PBC=∠ABC,∠PCB=∠ACB,∠QBC=∠MBC,∠QCB=∠QCB,
∴∠PBC+∠QBC=(∠ABC+∠MBC),
∠PCB+∠QCB=(∠ACB+∠MCB),
∵∠ABC+∠MBC=180°,∠ACB+∠MCB=180°,
∴∠PBQ=∠PCQ=90°,
∴∠P+∠Q=360°﹣∠PBQ﹣∠PCQ=180°.
