5.2运动的合成与分解课件 (共20张PPT) 高一下学期物理人教版(2019)必修第二册
文档属性
| 名称 | 5.2运动的合成与分解课件 (共20张PPT) 高一下学期物理人教版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 44.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-10-22 15:22:32 | ||
图片预览







文档简介
(共20张PPT)
第五章 抛体运动
第2节
运动的合成与分解
在一次抗洪抢险中,一些工人被泛滥的河流阻隔在滩涂上,滩涂正对岸上的救援人员试图游泳过去解救被困工人,你认为救援人员应如何游泳,才能靠近被困工人呢?
00
思考与讨论
如何分析蜡块的运动?
00
实验:观察蜡块的运动
蜡块运动的轨迹的分析
第一部分
01
x
y
y
x
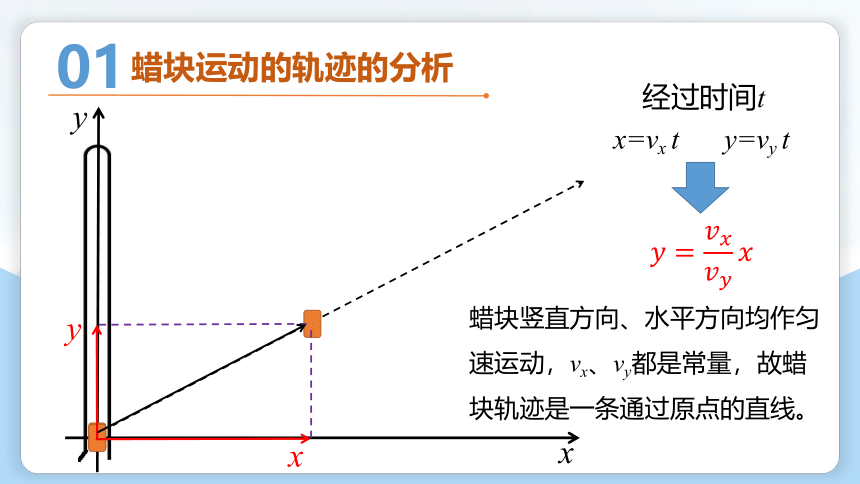
蜡块竖直方向、水平方向均作匀速运动,vx、vy都是常量,故蜡块轨迹是一条通过原点的直线。
经过时间t
x=vx t
y=vy t
蜡块运动的轨迹的分析
01
x
y
vx
vy
v
θ
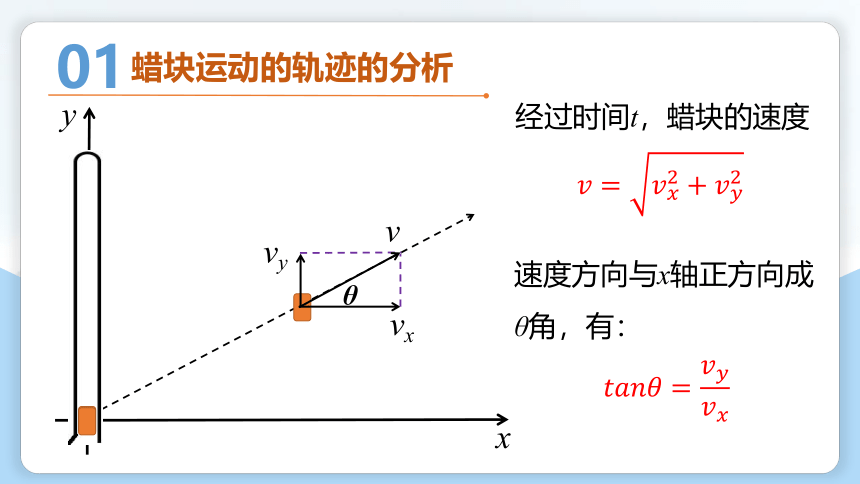
经过时间t,蜡块的速度
速度方向与x轴正方向成θ角,有:
蜡块运动的轨迹的分析
认识中的太阳系
实际中的太阳系
00
重新认识太阳系的运动
合运动与分运动
第二部分
vx
vy
v
分运动
分运动
合运动
分运动
合运动
运动的合成
运动的分解
等效替代,遵从矢量运算法则
02
合运动与分运动
某商场设有步行楼梯和自动扶梯,步行楼梯每级的高度是0.15m,自动扶梯与水 平面的夹角为30°,自动扶梯前进的速度是0.76m/s。有甲、乙两位顾客,分别从自 动扶梯和步行楼梯的起点同时上楼,甲在自动扶梯上站立不动,乙在步行楼梯上以每秒上两个台阶的速度匀速上楼哪位顾客先到达楼上?如果该楼层高4.56m,甲上楼用了多少时间?
解:甲在竖直方向的速度
v甲y =v甲 sin θ=0.76 ×sin 30°m/s =0.38 m/s
乙在竖直方向的速度
因此v甲y > v乙 ,甲先到楼上。
甲比乙先到达楼上,甲上楼用了 12 s
00
小试牛刀
有了上述结论,我们再看救援人员救人问题。
被困工人
水流方向
A
B
C
v水
v救援
v合
如果救援人员的头指向被困群众,救援人员会到达被困工人处吗?
救援人员在水中同时参与了两个分运动:(1)沿人头方向。(2)沿水流方向。
合速度偏向了下游!
救命啊!
船跑哪去了?我们在这儿呢!
00
思考与讨论
小船渡河
第三部分
若上述情形简化为下图所示,救援人员与被困工人所处B点的距离为d,救援人员从岸边的A点出发,欲用最短时间游到被困工人所在滩涂的岸边。已知河水流速为v水,救援人员在静水中的速度为v救援。 那么救援人员如何游?最短时间为多少?此时救援人员的位移和速度分别为多大?
A
d
B
v水
滩涂岸边
被困工人
解:由于水流速度始终沿河岸方向,不能提供指向滩涂岸边的分速度。因此若要渡河时间最短,只要使船头垂直于河岸航行即可。
由图可知,,此时救援人员的位移
,速度,位移方向满足
v水
v救援
v合
θ
s
03
小船渡河
若上述情形简化为下图所示,救援人员与被困工人所处B点的距离为d,救援人员从岸边的A点出发,欲以最短距离游到被困工人所在滩涂的岸边。已知河水流速为v水,救援人员在静水中的速度为v救援,且v水
A
d
B
v水
滩涂岸边
被困工人
解:由于水流速度始终沿河岸方向,不能提供指向滩涂岸边的分速度。因此若要渡河时间最短,只要使船头垂直于河岸航行即可。
由图可知,此时救援人员的最短位移为,
速度,速度方向满足
v合
v救援
v水
β
课后思考,若v水>v救援,救援人员如何游才能使游过的位移最小?最小位移为多大?
03
小船渡河
某船在静水中的速度v1=5m/s,要渡过宽30m的河,河水的流速v2=4m/s,下列说法正确的是( )
A. 该船渡河所用时间至少是7.5s
B. 该船的航程至少等于30m
C. 若河水的流速增大,则渡河的最短时间变长
D. 该船以最短时间渡河时的位移大小为30m
B
00
小试牛刀
课堂小结
巩固提升
第四部分
1.竖直放置的两端封闭的玻璃管中注满清水,内有一个蜡块能在水中以0.3m/s的速度匀速上浮。在蜡块从玻璃管的下端匀速上浮的同时,使玻璃管沿水平方向匀速向右运动,测得蜡块实际运动方向与水平方向成37°角,如图所示。在蜡块从底端上升到顶端的过程中,玻璃管水平方向的移动速度为 m/s。(sin 37°=0.6,cos 37°=0.8)
vx
vy
0.4
精选练习
2.武装泅渡的战士以一定的速度垂直河岸向对岸游去,当水流匀速时,关于他过河所需时间、发生的位移与水速的关系正确的是( )
A.水速小时,位移小,时间短
B.水速大时,位移大,时间短
C.水速大时,位移大,时间不变
D .位移、时间与水速无关
C
精选练习
3.质量为0.2kg的物体在水平面运动,它的两个正交分速度随时间变化的图线分别如图甲、乙所示,由图可求得。
(1) 4s末物体的速度大小为多少?
(2) 0~6s内物体的位移大小为多少?
(3) 2s末物体的加速度大小和速度大小
加速度方向和速度方向之间的夹角多大?
(3)a=1m/s2 沿x轴正方向
与x轴正方向的夹角为450
(1)(2)
精选练习
第五章 抛体运动
第2节
运动的合成与分解
在一次抗洪抢险中,一些工人被泛滥的河流阻隔在滩涂上,滩涂正对岸上的救援人员试图游泳过去解救被困工人,你认为救援人员应如何游泳,才能靠近被困工人呢?
00
思考与讨论
如何分析蜡块的运动?
00
实验:观察蜡块的运动
蜡块运动的轨迹的分析
第一部分
01
x
y
y
x
蜡块竖直方向、水平方向均作匀速运动,vx、vy都是常量,故蜡块轨迹是一条通过原点的直线。
经过时间t
x=vx t
y=vy t
蜡块运动的轨迹的分析
01
x
y
vx
vy
v
θ
经过时间t,蜡块的速度
速度方向与x轴正方向成θ角,有:
蜡块运动的轨迹的分析
认识中的太阳系
实际中的太阳系
00
重新认识太阳系的运动
合运动与分运动
第二部分
vx
vy
v
分运动
分运动
合运动
分运动
合运动
运动的合成
运动的分解
等效替代,遵从矢量运算法则
02
合运动与分运动
某商场设有步行楼梯和自动扶梯,步行楼梯每级的高度是0.15m,自动扶梯与水 平面的夹角为30°,自动扶梯前进的速度是0.76m/s。有甲、乙两位顾客,分别从自 动扶梯和步行楼梯的起点同时上楼,甲在自动扶梯上站立不动,乙在步行楼梯上以每秒上两个台阶的速度匀速上楼哪位顾客先到达楼上?如果该楼层高4.56m,甲上楼用了多少时间?
解:甲在竖直方向的速度
v甲y =v甲 sin θ=0.76 ×sin 30°m/s =0.38 m/s
乙在竖直方向的速度
因此v甲y > v乙 ,甲先到楼上。
甲比乙先到达楼上,甲上楼用了 12 s
00
小试牛刀
有了上述结论,我们再看救援人员救人问题。
被困工人
水流方向
A
B
C
v水
v救援
v合
如果救援人员的头指向被困群众,救援人员会到达被困工人处吗?
救援人员在水中同时参与了两个分运动:(1)沿人头方向。(2)沿水流方向。
合速度偏向了下游!
救命啊!
船跑哪去了?我们在这儿呢!
00
思考与讨论
小船渡河
第三部分
若上述情形简化为下图所示,救援人员与被困工人所处B点的距离为d,救援人员从岸边的A点出发,欲用最短时间游到被困工人所在滩涂的岸边。已知河水流速为v水,救援人员在静水中的速度为v救援。 那么救援人员如何游?最短时间为多少?此时救援人员的位移和速度分别为多大?
A
d
B
v水
滩涂岸边
被困工人
解:由于水流速度始终沿河岸方向,不能提供指向滩涂岸边的分速度。因此若要渡河时间最短,只要使船头垂直于河岸航行即可。
由图可知,,此时救援人员的位移
,速度,位移方向满足
v水
v救援
v合
θ
s
03
小船渡河
若上述情形简化为下图所示,救援人员与被困工人所处B点的距离为d,救援人员从岸边的A点出发,欲以最短距离游到被困工人所在滩涂的岸边。已知河水流速为v水,救援人员在静水中的速度为v救援,且v水
A
d
B
v水
滩涂岸边
被困工人
解:由于水流速度始终沿河岸方向,不能提供指向滩涂岸边的分速度。因此若要渡河时间最短,只要使船头垂直于河岸航行即可。
由图可知,此时救援人员的最短位移为,
速度,速度方向满足
v合
v救援
v水
β
课后思考,若v水>v救援,救援人员如何游才能使游过的位移最小?最小位移为多大?
03
小船渡河
某船在静水中的速度v1=5m/s,要渡过宽30m的河,河水的流速v2=4m/s,下列说法正确的是( )
A. 该船渡河所用时间至少是7.5s
B. 该船的航程至少等于30m
C. 若河水的流速增大,则渡河的最短时间变长
D. 该船以最短时间渡河时的位移大小为30m
B
00
小试牛刀
课堂小结
巩固提升
第四部分
1.竖直放置的两端封闭的玻璃管中注满清水,内有一个蜡块能在水中以0.3m/s的速度匀速上浮。在蜡块从玻璃管的下端匀速上浮的同时,使玻璃管沿水平方向匀速向右运动,测得蜡块实际运动方向与水平方向成37°角,如图所示。在蜡块从底端上升到顶端的过程中,玻璃管水平方向的移动速度为 m/s。(sin 37°=0.6,cos 37°=0.8)
vx
vy
0.4
精选练习
2.武装泅渡的战士以一定的速度垂直河岸向对岸游去,当水流匀速时,关于他过河所需时间、发生的位移与水速的关系正确的是( )
A.水速小时,位移小,时间短
B.水速大时,位移大,时间短
C.水速大时,位移大,时间不变
D .位移、时间与水速无关
C
精选练习
3.质量为0.2kg的物体在水平面运动,它的两个正交分速度随时间变化的图线分别如图甲、乙所示,由图可求得。
(1) 4s末物体的速度大小为多少?
(2) 0~6s内物体的位移大小为多少?
(3) 2s末物体的加速度大小和速度大小
加速度方向和速度方向之间的夹角多大?
(3)a=1m/s2 沿x轴正方向
与x轴正方向的夹角为450
(1)(2)
精选练习
