专题27.22相似三角形的性质 培优篇 专项练习(含解析)2023-2024学年九年级数学下册人教版专项讲练
文档属性
| 名称 | 专题27.22相似三角形的性质 培优篇 专项练习(含解析)2023-2024学年九年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 16:45:19 | ||
图片预览

文档简介
专题27.22 相似三角形的性质(培优篇)(专项练习)
一、单选题
1.如图,在平面直角坐标系中,已知点A坐标(0,3),点B坐标(4,0),将点O沿直线对折,点O恰好落在∠OAB的平分线上的O’处,则的值为( )
A. B. C. D.
2.如图,是的高,是的中点,交于于.若则的长为( )
A. B. C. D.
3.如图,在中,,,,点在边上,并且,点为边上的动点,将沿直线翻折,点落在点处,则点到边的距离的最小值是
A. B.1 C. D.
4.如图,四边形中,,,,若,,则的值为( )
A. B.2 C. D.
5.如图,点E从矩形ABCD的顶点B出发,沿射线BC的方向以每秒1个单位的速度运动,过E作EF⊥AE交直线DC于F点,如图2 是点E运动时CF的长度y随时间t变化的图象,其中M点是一段曲线(抛物线的一部分)的最高点,过M点作MN⊥y轴交图象于N点,则N点坐标是( )
A.(5,2) B.(,2) C.(,2) D.(,2)
6.如图,在直角坐标系xOy中,A(﹣4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )
A.(1,) B.(,) C.(,2) D.(,2)
7.如图,四边形ABCD是边长为2的菱形,且有一个内角为72°,现将其绕点D顺时针旋转得到菱形A'B'C'D,线段AB与线段B'C'交于点P,连接BB'.当五边形A'B'BCD为正五边形时,即长为( )
A.1 B. C. D.
8.如图,将一个面积为24的正方形纸片沿图中的3条裁切线剪开后,恰好能拼成一个邻边不相等的矩形.若裁切线AB的长为6,则裁切线CD的长是( )
A. B. C. D.
9.如图,将矩形ABCD折叠,使点D落在AB上点D′处,折痕为AE;再次折叠,使点C落在ED′上点C′处,连接FC′并延长交AE于点G.若AB=8,AD=5,则FG长为( )
A. B. C. D.4
10.由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示,延长AH交CD于点P,若,,则小正方形边长GF的长是( )
A. B. C.3 D.
二、填空题
11.如图,在△ABC中,D为BC中点,将△ABD沿AD折叠得到△AED,连接EC,已知BC=6,AD=2,且S△CDE=,则点A到DE的距离为 .
12.如图,E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,连接AC、HE、EC、GA、GF,已知AG⊥GF,AC=2,则AB的长为 .
13.在平面直角坐标系中,如图,,点,点C在y轴上且,连接.现给出以下结论:
①连接,则;
②的周长是一个固定值;
③的最小值为1;
④当取最小值时,.
其中正确的是 (写出所有正确结论的序号)
14.如图,在平面直角坐标系中,点A(0,1),点B为直线y=x上的一个动点,∠ABC=90°,BC=2AB,则OC的最小值为 .
15.已知是直角三角形,连接以为底作直角三角形且是边上的一点,连接和且则长为 .
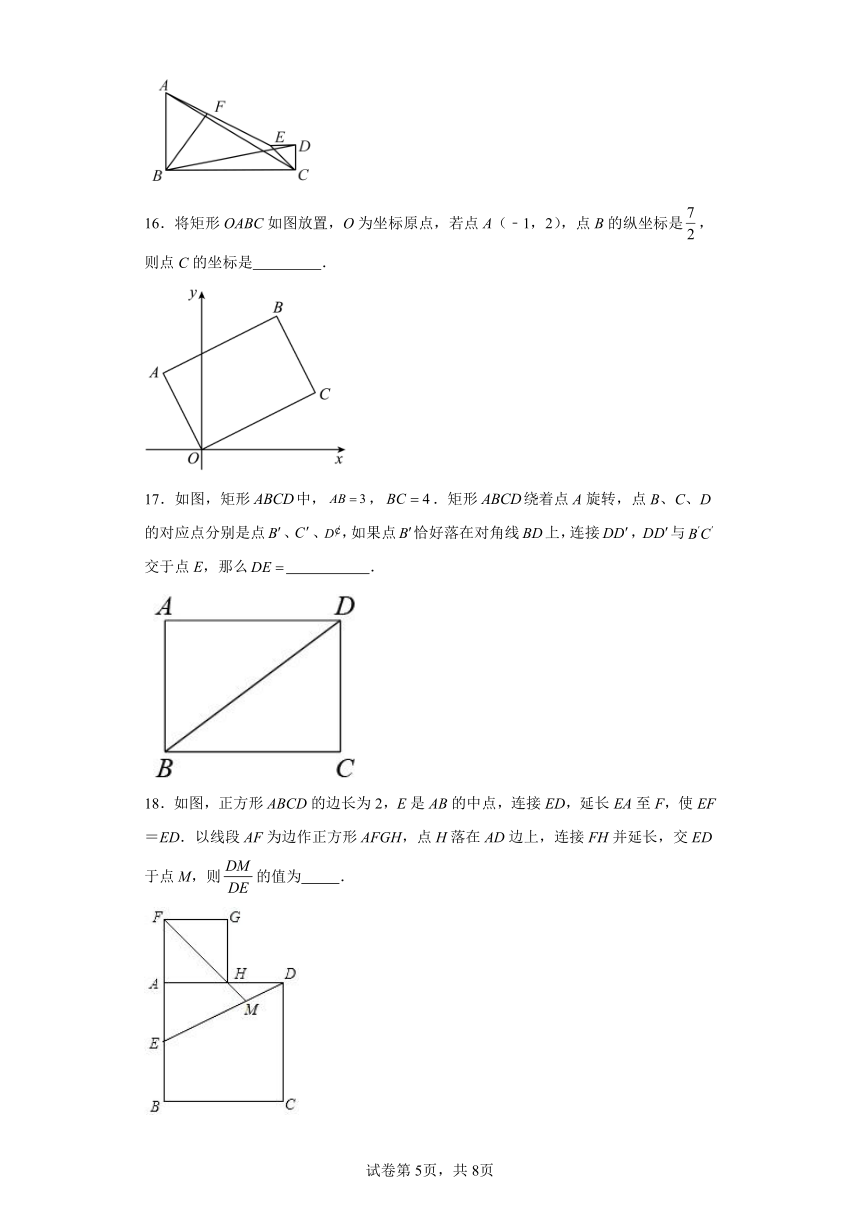
16.将矩形OABC如图放置,O为坐标原点,若点A(﹣1,2),点B的纵坐标是,则点C的坐标是 .
17.如图,矩形中,,.矩形绕着点A旋转,点B、C、D的对应点分别是点、、,如果点恰好落在对角线上,连接,与交于点E,那么 .
18.如图,正方形ABCD的边长为2,E是AB的中点,连接ED,延长EA至F,使EF=ED.以线段AF为边作正方形AFGH,点H落在AD边上,连接FH并延长,交ED于点M,则的值为 .
三、解答题
19.已知矩形ABCD,点E在AD边上,连接BE、BD,∠BED=2∠BDC,BE=25,BC=32,则CD的长度为 .
20.在正方形ABCD中,P为AB边上一点,将△BCP沿CP折叠,得到△FCP.
(1)如图1,延长PF交AD于E,求证:EF=ED;
(2)如图2,DF,CP的延长线交于点G,求的值.
21.如图,在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿CB向点B方向运动,如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
(1)当t=3秒时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式.
(3)当t为多少秒时,以点C,P,Q为顶点的三角形与△ABC相似?
22.如图1.已知四边形是矩形.点在的延长线上.与相交于点,与相交于点
求证:;
若,求的长;
如图2,连接,求证:.
23.如图,正方形ABCD中,P是对角线AC上的一个动点(不与A、C重合),连结BP,将BP绕点B顺时针旋转到BQ,连结QP交BC于点E,QP延长线与边AD交于点F.
(1)连结CQ,求证:;
(2)若,求的值;
(3)求证:.
24.【操作发现】
如图①,在正方形ABCD中,点N、M分别在边BC、CD上,连结AM、AN、MN.
∠MAN=45°,将△AMD绕点A顺时针旋转90°,点D与点B重合,得到△ABE.易证:△ANM≌△ANE,从而得DM+BN=MN.
【实践探究】
(1)在图①条件下,若CN=3,CM=4,则正方形ABCD的边长是 .
(2)如图②,点M、N分别在边CD、AB上,且BN=DM.点E、F分别在BM、DN上,∠EAF=45°,连接EF,猜想三条线段EF、BE、DF之间满足的数量关系,并说明理由.
【拓展】
(3)如图③,在矩形ABCD中,AB=3,AD=4,点M、N分别在边DC、BC上,连结AM,AN,已知∠MAN=45°,BN=1,求DM的长.
试卷第2页,共2页
试卷第1页,共1页
参考答案:
1.D
【分析】假设直线与∠OAB的平分线交x轴点C,交y轴于D,易求得OA=3,OB=4,AB=5,OD=b,且直线与AB平行,利用角平分线性质可得,再由平行线分线段成比例得即,解得,结合图象,,利用排除法即可得到答案.
【详解】假设直线与∠OAB的平分线交x轴点C,交y轴于D,如图:
∵A(0,3),B(4,0),
∴OA=3,OB=4,AB=5,且直线AB斜率等于,
由直线知OD=b,且直线与AB平行,
∵AC平分∠OAB,
∴,
∵直线与AB平行,
∴即,
解得,
结合图象直线的位置,b的范围为,
利用排除法,
故选D.
【点睛】本题考查了角平分线的性质和平行线分线段成比例,利用假设法和排除法解答是选择题的一种技巧.
2.C
【分析】延长BC交FE的延长线于点H,推出,通过证明,得出,继而得出,再证明,得出,再证明,从而得出答案.
【详解】解:延长BC交FE的延长线于点H,
∵
∴
∴
∴
∵是CD的中点
∴
∴
∴
∴
∴
∴
∴
∵
∴
∵
∴
∴
∵
∴
∵
∴
∴
∴
∴
故选:C.
【点睛】本题考查的知识点是相似三角形的判定及性质,作出辅助线后多次利用相似三角形的性质得出CH、AE的值是解此题的关键.
3.D
【分析】先依据勾股定理求得的长,然后依据翻折的性质可知,故此点在以为圆心,以2为半径的圆上,依据垂线段最短可知当时,点到的距离最短,然后依据题意画出图形,最后,利用相似三角形的性质求解即可.
【详解】解:如图所示:当.
由翻折的性质可知:,.
,
.
由垂线段最短可知此时有最小值.
又为定值,
有最小值.
又,,
.
∴,
∵CF=2,AC=6,BC=8,
∴AF=4,AB==10,
∴即,
∴.
.
故选:.
【点睛】本题考查翻折变换、最短问题、相似三角形的判定和性质、勾股定理.垂线段最短等知识,解题的关键是正确找到点P位置,属于中考常考题型.
4.C
【分析】延长AD、BC交于点E,过点D作DFBE,垂足为F,如图所示,易发现,通过对应边成比例,可求解出DE、CE,再利用即可求出DF、BF.
【详解】延长AD、BC交于点E,过点D作DFBE,垂足为F,如图所示,
,,
,
,
又,
,
设DE=x,CE=y,
,
整理可得关于x,y的二元一次方程组,
,
解得,
,
故选C.
【点睛】利用三角形相似,找到边与边的比例关系,可以求出未知边长,再利用勾股定理即可求解.
5.D
【分析】当点运动到点位置时,,则,当点运动到中点位置时,,即,证明,当在的延长线上时,且,根据相似三角形的性质求得的长,即可求得点的横坐标
【详解】解:根据函数图象可知,当点运动到点位置时,,则,
当点运动到中点位置时,,即,
∴
四边形是矩形
的纵坐标相等,则当在的延长线上时,,,,
,
即
解得,(舍)
即点的坐标为(,2)
故选:D
【点睛】本题考查了动点问题函数图象,相似三角形的性质与判定,从函数图像获取信息是解题的关键.
6.B
【详解】根据相似三角形对应边成比例,由△COB∽△CAO求出CB、AC的关系AC=4CB,从而得到,过点C作CD⊥y轴于点D,然后求出△AOB和△CDB相似,根据相似三角形对应边成比例求出CD=、BD=,再求出OD=,最后写出点C的坐标为(,).
故选:B.
点睛:本题考查了相似三角形的性质,坐标与图形性质,主要利用了相似三角形对应边成比例,求出是解题的关键,也是本题的难点.
7.B
【分析】先计算得出∠CDC'=∠ADA'=∠ADC'=36°,得到点C'在对角线BD上,再证明△BDA∽△BAC',求得BP= C'A= C'B=,进一步计算即可求解.
【详解】解:连接BC',AC',如图:
∵五边形A'B'BCD为正五边形,
∴∠CDA'==108°,
∵菱形ABCD绕点D顺时针旋转得到菱形A'B'C'D,且∠ADC=72°,
∴∠A'DC'=∠ADC=72°,
∴∠CDC'=∠ADA'=108°-72°=36°,
∴∠CDC'=∠ADA'=∠ADC'=36°,
∴点C'在对角线BD上,∠ABC'=36°,
由旋转的性质知AD=AB= DC'=2,
∴∠DC'A=∠DAC'=72°,
∴∠C'AB=36°,
∴C'A= C'B,
设C'A= C'B=x,则BD= x+2,
∵∠BDA=∠BAC'=36°,
∴△BDA∽△BAC',
∴DA:AC'=BD:BA,即2:x=( x+2):2,
整理得:x2+2x-4=0,
解得x=,(负值已舍)
∵∠C'BP=36°,∠BC'P=72°,
∴∠C'PB=72°,
∴BP= C'A= C'B=,
∴AP=3-,
∴,
故选:B.
【点睛】本题考查了正多边的性质,菱形的性质,相似三角形的判定和性质,二次根式的混合运算,解题的关键是学会利用参数构建方程解决问题.
8.A
【分析】画出裁切后的矩形,再利用相似求解即可.
【详解】如图所示,四边形ABQN是裁切后的矩形:
∴,,
∴
∴
∵正方形HFG的面积是24
∴
∴
∴
∴
∴
∴
解得
故选:A.
【点睛】本题考查相似三角形的判定与性质、矩形的性质,解题的关键是正确的画出裁切后拼成的矩形.
9.C
【分析】过点G作GI⊥AB,GH⊥ED',垂足分别为I、H,由折叠的性质可得C′E=5-4=1,在Rt△EFC′中,设FC′=x,则EF=3-x,由勾股定理得:12+(3-x)2=x2,解得:x=,再证明△BC′D'∽△C′GH,设C′H=3m,则GH=4m,C′G=5m,则HD'=GI=AI=4-3m,ID'=5-(4-3m)=1+3m=GH=4m,可得到C′G=5m=5,从而解决问题.
【详解】解:由折叠的性质得,∠AD'E=∠D=90°,AD=AD',
又∵∠DAB=90°,
∴四边形ADED'是矩形,
∵AD=AD',
∴四边形ADED'是正方形,
过点G作GI⊥AB,GH⊥ED',垂足分别为I、H,
∵AD'ED是正方形,
∴AD=DE=ED'=AD'=5,BC=BC′=5,∠C=∠BC′F=90°,FC=FC′,
∴D'B=EC=8-5=3,
在Rt△C′BD'中,C′D'=4,
∴C′E=5-4=1,
在Rt△EFC′中,设FC′=x,则EF=3-x,由勾股定理得:
12+(3-x)2=x2,
解得:x=,
∵∠BC′D'+∠GC′H=90°,∠GC′H+∠C′GH=90°,
∴∠BC′D'=∠C′GH,
又∵∠GHC′=∠BD'C′=90°,
∴△BC′D'∽△C′GH,
∴C′H:GH:C′G=BD':C′D':BC′=3:4:5,
设C′H=3m,则GH=4m,C′G=5m,
∴HD'=GI=AI=4-3m,ID'=5-(4-3m)=1+3m=GH=4m,
解得:m=1,
∴C′G=5m=5,
∴FG=;
故选:C.
【点睛】本题主要考查了矩形的性质,正方形的判定与性质,翻折的性质,勾股定理,相似三角形的判定与性质等知识,作辅助线构造三角形相似是解题的关键.
10.B
【分析】过点E作EM⊥AB于点M,证明△AED∽△HMD,可得, 由MH∥DP,可得,从而可得结论.
【详解】解:∵△ADE≌△DCH≌△CBG≌△BAF,
∴AE=DH,DE=CH,
∵四边形GFEH是正方形,
∴EH=EF=HG=GF,∠HFA=45°=∠EHF,
∵AP⊥HF,
∴∠FAH=∠AFH=45°=∠AHE,
∴AH=FH,AE=HE,
∴AF=2AE,
设AE=a,则AF=DE=2a, 如图过点H作HM⊥AD于M,
∴
∵∠DMH=∠AED=90°,∠ADE=∠MDH,
∴△AED∽△HMD,
∴,
∴,,
∴,
∵AD⊥CD, ∴MH∥DP,
∴ ,
∵AP=10,
∴AH=6,
∴EH==GF,
故选:B.
【点睛】本题考查了正方形的性质,勾股定理,相似三角形的判定和性质,添加恰当辅助线构造相似三角形是解题的关键.
11..
【分析】过点E作EF⊥BC于F,AG⊥DE于G,AH⊥BC于H,由将△ABD沿AD折叠得到△AED,可得,可证,由D为BC中点,BC=6,可求,由S△CDE=,可求,在Rt△EDF中,由勾股定理,可求FC=,在Rt△ECF中,由勾股定理,可证,可得 ,可求即可
【详解】解:过点E作EF⊥BC于F,AG⊥DE于G,AH⊥BC于H,
∵将△ABD沿AD折叠得到△AED,
∴,
∴AD为∠BDE的平分线,
∵EF⊥BC于F,AG⊥DE于G,
∴,
∵D为BC中点,BC=6,
∴,
∵S△CDE=,
∴,
∴,
在Rt△EDF中,由勾股定理,
∴FC=DC-DF=3-,
在Rt△ECF中,由勾股定理,
∵DE=DC,
∴,
由外角性质,,
∴,
,
∴,
∴即,
∴,
∴AG=,
故答案为:.
【点睛】本题考查折叠性质,角平分线性质,三角形面积,勾股定理,相似三角形判定与性质,掌握折叠性质,角平分线性质,三角形面积,勾股定理,相似三角形判定与性质,利用辅助线画出准去图形是解题关键.
12.
【分析】如图,连接BD.由△ADG∽△GCF,设CF=BF=a,CG=DG=b,可得=,推出,可得b=a,在Rt△GCF中,利用勾股定理求出b,即可解决问题;
【详解】如图,连接BD.
∵四边形ABCD是矩形,
∴∠ADC=∠DCB=90°,AC=BD=2,
∵CG=DG,CF=FB,
∴GF=BD=,
∵AG⊥FG,
∴∠AGF=90°,
∴∠DAG+∠AGD=90°,∠AGD+∠CGF=90°,
∴∠DAG=∠CGF,
∴△ADG∽△GCF,
设CF=BF=a,CG=DG=b,
∴=,
∴,
∴b2=2a2,
∵a>0.b>0,
∴b=a,
在Rt△GCF中,3a2=3,
∴a=1,
∴AB=2b=2.
故答案为2.
【点睛】本题考查三角形中位线定理、矩形的性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
13.①③④
【分析】①利用勾股定理计算出AC的长,进行判断;②表示出△OAB的周长即可判断;③利用图形变形,将BC放在三角形中根据三角形的三边关系进行判断;④利用三垂直模型及三角形相似求出OA的长即可.
【详解】解:①∵A(a,0),OA=OC,
∴ACa,
故①正确;
②C△OAB=OA+AB+OB=a+3+2,
∵3﹣2a<3+2,
∴C△OAB不是一个固定值,
故②错误;
③如图,将△OBC绕点O顺时针旋转90°,得到△ODA,
则OB=OD,BC=AD,∠BOD=90°,
∴BD4,
在△ABD中,AD>BD﹣AB,
当B,A,D三点共线时,AD最短,即BC最短,
此时BC=DA﹣AB=4﹣3=1,
故③正确;
④如图,当B,A,D三点共线时,作BE,DF垂直于x轴,垂足为E,F,
则∠OEB=∠DFO=90°,∠1+∠2=90°,
又∠BOD=∠2+∠3=90°,
∴∠1=∠3,
又OB=OD,
∴△BOE≌△ODF(AAS),
设B(x,y),则DF=OE=x,OF=BE=y,且x2+y2=(2)2=8,
由BE⊥x轴,DF⊥x轴得BE∥DF,
∴△ADF∽△ABE,
∴,即,
∴y=3x,
把y=3x代入x2+y2=(2)2=8得,
x2+9x2=8,
解得x=±(负值舍去),
∴y,
由△ADF∽△ABE得,,
∴AE=3AF,
即a﹣x=3(y﹣a),
a﹣x=3y﹣3a,
∴a,
即OA.
故④正确.
故答案为:①③④.
【点睛】本题考查勾股定理,相似以及两点间的距离公式,熟练掌握勾股定理是解题关键.
14.
【分析】分析求OC最小即求AC最小,求AC最小即求AB最小,根据点到直线的距离公式求AB最小,继而代换求出OC最小.
【详解】连接OC,在△AOC中,
OCAC-OA
故求OC最短,即求AC最短
由题意知:∠ABC=,BC=2AB且点A(0,1),
设AB=m,BC=2m,AC= m
根据点到直线的距离可知,m最小= .
此时AB⊥直线y=x,点C在直线上
∴BC=
作BD⊥OA与点D,
在△ABD和△BOD中
∴△DOB∽△OBA
∴
又∵AB=m=
∴OB=
∴OC=
故答案为.
【点睛】本题主要考查了点到直线的距离公式及三角形相似的性质,正确掌握点到直线的距离公式及三角形相似的性质是解题的关键.
15.
【分析】将线段绕点顺时针旋转,得到线段,连接,HE,利用证明,得,,则,即可解决问题.
【详解】解:将线段绕点顺时针旋转,得到线段,连接,HE,
是等腰直角三角形,
∴∠HBD=45°
∵∠FBD=45°
∴点B、F、H共线
又是等腰直角三角形,
,,,
,
,,
,
,
,
,
,
,
故答案为:.
【点睛】本题主要考查了等腰直角三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质等知识,解题的关键是作辅助线构造全等三角形.
16.(3,)
【分析】过点A作AD⊥x轴,垂足为D,过点B作BF⊥x轴,垂足为F,过点C作CG⊥x轴,垂足为G,过点B作BE⊥CG,交GC的延长线于点E,通过证明△ADO≌△CEB,△ADO∽△OGC即可.
【详解】过点A作AD⊥x轴,垂足为D,过点B作BF⊥x轴,垂足为F,过点C作CG⊥x轴,垂足为G,过点B作BE⊥CG,交GC的延长线于点E,
∴四边形BFGE是矩形,∠ADO=∠CBE=90°,
∴BF=EG,
∵四边形OABC是矩形,
∴OA=CB,∠BCO=90°,
∴∠AOD=90°-∠COG=∠GCO=90°-∠BCE=∠CBE,
∴△ADO≌△CEB,△ADO∽△OGC,
∴AD=CE,,
∵点A(﹣1,2),点B的纵坐标是,
∴AD=CE=2,BF=EG=,CG=EG-CE=-2=,
∴,
解得OG=3,
故点C的坐标为(3,),
故答案为:(3,).
【点睛】本题考查了矩形的性质,三角形全等的判定和性质,三角形相似的判定和性质,坐标与线段的关系,熟练掌握矩形的性质,三角形的全等与系数是解题的关键.
17.
【分析】过A点作AF⊥BD,交BD于点F,利用勾股定理求出BD=5,在根据是矩形ABD的面积求出AF,进而可求出,进而求出,再证明,即有,DE可求.
【详解】过A点作AF⊥BD,交BD于点F,如图,
∵矩形中AB=3,BC=AD=4,∠BAC=90°,
∴,
∵,
∴,
∴,
根据旋转可知:,,,
∵,
∴,即,
∴,
根据旋转可知:,,,
∴根据两个等腰三角形中顶角相等,则其底角也相等,即,
∵,
∴,
∵,,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:.
【点睛】本题考查了旋转的性质,矩形的性质,勾股定理,等腰三角形的性质,相似三角形的判定与性质,求出是解答本题的关键.
18.
【分析】过点M作MN⊥AD于点N,根据勾股定理可得DE=EF=,根据四边形AFGH是正方形,可得AF=AH=EF﹣AE=,根据,可得△DMN∽△DEA,所以,即,即可设MN=NH=x,则DN=2x,DM=,再根据DN+NH=AD﹣AH,列式,求出x的值,进而可以解决问题.
【详解】解:如图,过点M作MN⊥AD于点N,
∵正方形ABCD的边长为2,E是AB的中点,
∴AD=AB=2,AE=1,∠EAD=90°,
∴,
∵四边形AFGH是正方形,
∴AF=AH=EF﹣AE=,
∵∠AHF=∠NHM=45°,
∴MN=NH,
∵,
∴△DMN∽△DEA,
∴,
∴,
设MN=NH=x,
则DN=2x,DM=,
∴DN+NH=AD﹣AH,
∴,
∴,
∴,
∴,
故答案为:.
【点睛】此题考查了正方形的性质和三角形相似的知识,解决本题的关键是找到相似三角形得出线段之间的关系.
19.24
【分析】过E作EF⊥BD于F,根据矩形的性质得到∠C=∠ADC=90°,于是得到∠ADB+∠BDC=90°,根据已知条件推出180°-∠AEB=2(90°-∠ADB),得到∠AEB=2∠EDB,根据等腰三角形的性质得到BF=BD,由平行线的性质得到∠ADB=∠DBC,等量代换得到∠EBF=∠DBC,推出△EBF∽△DBC,根据相似三角形的性质,求得BD=40,由勾股定理即可得到结论.
【详解】过作于,
∵四边形是矩形,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∴.
故答案为:24.
【点睛】本题考查了矩形的性质,相似三角形的判定和性质,平行线的性质,外角的性质,正确的作出辅助线构造相似三角形是解题的关键.
20.(1)证明见解析(2)
【分析】(1)连接CE,通过全等三角形的判定,得到Rt△CFE≌Rt△CDE,进而得出结论;
(2)连接BG、BF、BD,作CH⊥DF,垂足为H.依据△CFG≌△CBG,可得GF=GB,进而得出△GBF是等腰直角三角形,故BF=BG.再判定△BGA∽△FBD,即可得到.
【详解】(1)如图1,连接CE,
∵四边形ABCD是正方形,
∴BC=CD,∠B=∠D=90°.
∵△PBC和△FPC关于PC对称,
∴BC=CF,∠B=∠PFC=90°.
∴∠EFC=90°.
∴∠EFC=∠D=90°,CF=CD.
∵CE=CE,
∴Rt△EFC≌Rt△DFC(HL).
∴EF=ED.
(2)如图2,连接BG、BF、BD,作CH⊥DF,垂足为H.
∵四边形ABCD是正方形,
∴BC=CD.
∵CH⊥DF,
∴∠HCF=,
∵△PBC和△FPC关于PC对称,
∴BC=CF,∠FCG=∠BCG.
∴EB⊥CG.
又∵CG=CG,
∴△CFG≌△CBG.
∴GF=GB.
∵∠HCF=,∠FCG=∠BCG=,
∴∠HCK==45°.
∴∠PFH=135°.
∴∠GFB=45°.
∴∠GBF=45°.
∴△GBF是等腰直角三角形.
∴.
∵∠ABD=45°,
∴∠GBA=∠FBD.
∵,
∴△BGA∽△FBD.
∴.
【点睛】本题主要考查了全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,等腰直角三角形的判定与性质的综合运用,解决问题的关键是作辅助线构造等腰直角三角形,全等三角形以及相似三角形,利用相似三角形的对应边成比例得出结论.
21.(1)10cm;(2);(3)t=3或t=
【分析】(1)在Rt△CPQ中,当t=3秒,可知CP、CQ的长,运用勾股定理可将PQ的长求出;
(2)由点P,点Q的运动速度和运动时间,又知AC,BC的长,可将CP、CQ用含t的表达式求出,代入直角三角形面积公式=CP×CQ求解;
(3)应分两种情况:当Rt△CPQ∽Rt△CAB时,根据,可将时间t求出;当Rt△CPQ∽Rt△CBA时,根据,可求出时间t.
【详解】由题意得AP=4t,CQ=2t,则CP=20﹣4t,
(1)当t=3秒时,CP=20﹣4t=8cm,CQ=2t=6cm,
由勾股定理得PQ=;
(2)由题意得AP=4t,CQ=2t,则CP=20﹣4t,
因此Rt△CPQ的面积为S=;
(3)分两种情况:
①当Rt△CPQ∽Rt△CAB时,
,即,
解得:t=3秒;
②当Rt△CPQ∽Rt△CBA时,
,即,
解得:t=秒.
因此t=3秒或t=秒时,以点C、P、Q为顶点的三角形与△ABC相似
【点睛】本题主要考查了相似三角形性质以及勾股定理的运用,在解第三问时应分两种情况进行求解防止漏解或错解,注意方程思想与分类讨论思想的应用是解此题的关键.
22.(1)见解析;(2);(3)见解析
【分析】(1)由矩形的形及已知证得△EAF≌△DAB,则有∠E=∠ADB,进而证得∠EGB=90 即可证得结论;
(2)设AE=x,利用矩形性质知AF∥BC,则有,进而得到x的方程,解之即可;
(3)在EF上截取EH=DG,进而证明△EHA≌△DGA,得到∠EAH=∠DAG,AH=AG,则证得△HAG为等腰直角三角形,即可得证结论.
【详解】(1)∵四边形ABCD是矩形,
∴∠BAD=∠EAD=90 ,AO=BC,AD∥BC,
在△EAF和△DAB,
,
∴△EAF≌△DAB(SAS),
∴∠E=∠BDA,
∵∠BDA+∠ABD=90 ,
∴∠E+∠ABD=90 ,
∴∠EGB=90 ,
∴BG⊥EC;
(2)设AE=x,则EB=1+x,BC=AD=AE=x,
∵AF∥BC,∠E=∠E,
∴△EAF∽△EBC,
∴,又AF=AB=1,
∴即,
解得:,(舍去)
即AE=;
(3)在EG上截取EH=DG,连接AH,
在△EAH和△DAG,
,
∴△EAH≌△DAG(SAS),
∴∠EAH=∠DAG,AH=AG,
∵∠EAH+∠DAH=90 ,
∴∠DAG+∠DAH=90 ,
∴∠HAG=90 ,
∴△GAH是等腰直角三角形,
∴即,
∴GH=AG,
∵GH=EG-EH=EG-DG,
∴.
【点睛】本题主要考查了矩形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、直角定义、相似三角形的判定与性质、解一元二次方程等知识,涉及知识面广,解答的关键是认真审题,提取相关信息,利用截长补短等解题方法确定解题思路,进而推理、探究、发现和计算.
23.(1)见解析;(2) ;(3)见解析
【分析】(1)由旋转知△PBQ为等腰直角三角形,得到PB=QB,∠PBQ=90°,进而证明△APB≌△CQB即可;
(2)设AP=x,则AC=4x,PC=3x,由(1)知CQ=AP=x,又△ABC为等腰直角三角形,所以BC=,PQ=,再证明△BQE∽△BCQ,由此求出BE,进而求出CE:BC的值;
(3)在CE上截取CG,并使CG=FA,证明△PFA≌△QGC,进而得到PF=QG,然后再证明∠QGE=∠QEG即可得到QG=EQ,进而求解.
【详解】解:∵四边形ABCD为正方形,
∴AB=BC,∠ABC=90°,
∵BP绕点B顺时针旋转到BQ,
∴BP=BQ,∠PBQ=90°,
∴∠ABC-∠PBC=∠PBQ-∠PBC,
∴∠ABP=∠CBQ,
在△APB和△CQB中,
,
∴△APB≌△CQB(SAS),
∴AP=CQ.
(2) 设AP=x,则AC=4x,PC=3x,由(1)知CQ=AP=x,
△ABC为等腰直角三角形,∴BC=,
在Rt△PCQ中,由勾股定理有:,
且△PBQ为等腰直角三角形,
∴,
又∠BCQ=∠BAP=45°,∠BQE=45°,
∴∠BCQ=∠BQE=45°,且∠CBQ=∠CBQ,
∴△BQE∽△BCQ,
∴,代入数据:,
∴BE=,∴CE=BC-BE=,
∴,
故答案为:.
(3) 在CE上截取CG,并使CG=FA,如图所示:
∵∠FAP=∠GCQ=45°,
且由(1)知AP=CQ,且截取CG=FA,
故有△PFA≌△QGC(SAS),
∴PF=QG,∠PFA=∠CGQ,
又∵∠DFP=180°-∠PFA,∠QGE=180°-∠CGQ,
∴∠DFP=∠QGE,
∵DABC,
∴∠DFP=∠CEQ,
∴∠QGE=∠CEQ,
∴△QGE为等腰三角形,
∴GQ=QE,
故PF=QE.
【点睛】本题考查了正方形的性质、旋转的性质、三角形全等的判定和性质、相似三角形判定和性质的综合,具有一定的综合性,本题第(3)问关键是能想到在CE上截取CG,并使CG=FA这条辅助线.
24.(1)6;(2),见解析;(3)2
【分析】(1)根据旋转的性质证明△ABE≌△ADM得到BE=DM,又由∠ABE=∠D=90°,AE=AM,∠BAE=∠DAM,证出∠EAM=90°,得出∠MAN=∠EAN,再证明△AMN≌△EAN(SAS),得出MN=EN最后证出MN=BN+DM.在Rt△CMN中,由勾股定理计算即可得到正方形的边长;
(2 )先根据旋转的性质证明△AEG≌△AEF(SAS),再证明∠GBE=90°,再根据勾股定理即可得到;
(3)在AB上截取AP,在BC上截取BQ,使AP=AB=BQ=3,连结PQ交AM于点R,得到ABQP为正方形,再根据操作发现以及勾股定理即可得到答案;
【详解】(1)(1)解:∵四边形ABCD是正方形,
∴AB=CD=AD,∠BAD=∠C=∠D=90°,
由旋转得:△ABE≌△ADM,
∴BE=DM,∠ABE=∠D=90°,AE=AM,∠BAE=∠DAM,
∴∠BAE+∠BAM=∠DAM+∠BAM=∠BAD=90°,
即∠EAM=90°,
∵∠MAN=45°,
∴∠EAN=90°-45°=45°,
∴∠MAN=∠EAN,
在△AMN和△EAN中,
∴△AMN≌△EAN(SAS),
∴MN=EN.
∵EN=BE+BN=DM+BN,
∴MN=BN+DM.
在Rt△CMN中,
,
则BN+DM=5,
设正方形ABCD的边长为x,则BN=BC-CN=x-3,DM=CD-CM=x-4,
∴x-3+x-4=5,
解得:x=6,
即正方形ABCD的边长是6;
故答案为:6;
(2)数量关系为:,证明如下:
将△AFD绕点A顺时针旋转90°,点D与点B重合,得到△ABG,连结EG.
由旋转的性质得到:AF=AG,
又∵∠EAF=45°,
∴,
且AE=AE,
∴△AEG≌△AEF(SAS),
从而得EG=EF.(全等三角形对应边相等),
又∵BN=DM,BN∥DM,
∴四边形DMBN是平行四边形(一组对边平行且相等的四边形是平行四边形),
∴DN∥BM,
∴ (两直线平行,同位角相等),
∵,
∴(等量替换),
即:∠GBE=90°,
则,
∴;
(3)在AD上截取AP,在BC上截取BQ,使AP=AB=BQ=3,连结PQ交AM于点R,
易证ABQP为正方形,
由操作与发现知:PR+BN=RN.
设PR=x,则RQ=3﹣x,RN=1+x,QN=3-1=2
在Rt△QRN中,由勾股定理得:
,
即
解得:x=,
∴PR=
∵PQ∥DC,
∴△APR∽△ADM,
∴ (相似三角形对应边成比例)
∴
∴DM=2;
【点睛】本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、勾股定理、相似三角形的判定与性质等知识;本题综合性强,有一定难度,证明三角形全等和由勾股定理得出方程是解题的关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,在平面直角坐标系中,已知点A坐标(0,3),点B坐标(4,0),将点O沿直线对折,点O恰好落在∠OAB的平分线上的O’处,则的值为( )
A. B. C. D.
2.如图,是的高,是的中点,交于于.若则的长为( )
A. B. C. D.
3.如图,在中,,,,点在边上,并且,点为边上的动点,将沿直线翻折,点落在点处,则点到边的距离的最小值是
A. B.1 C. D.
4.如图,四边形中,,,,若,,则的值为( )
A. B.2 C. D.
5.如图,点E从矩形ABCD的顶点B出发,沿射线BC的方向以每秒1个单位的速度运动,过E作EF⊥AE交直线DC于F点,如图2 是点E运动时CF的长度y随时间t变化的图象,其中M点是一段曲线(抛物线的一部分)的最高点,过M点作MN⊥y轴交图象于N点,则N点坐标是( )
A.(5,2) B.(,2) C.(,2) D.(,2)
6.如图,在直角坐标系xOy中,A(﹣4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )
A.(1,) B.(,) C.(,2) D.(,2)
7.如图,四边形ABCD是边长为2的菱形,且有一个内角为72°,现将其绕点D顺时针旋转得到菱形A'B'C'D,线段AB与线段B'C'交于点P,连接BB'.当五边形A'B'BCD为正五边形时,即长为( )
A.1 B. C. D.
8.如图,将一个面积为24的正方形纸片沿图中的3条裁切线剪开后,恰好能拼成一个邻边不相等的矩形.若裁切线AB的长为6,则裁切线CD的长是( )
A. B. C. D.
9.如图,将矩形ABCD折叠,使点D落在AB上点D′处,折痕为AE;再次折叠,使点C落在ED′上点C′处,连接FC′并延长交AE于点G.若AB=8,AD=5,则FG长为( )
A. B. C. D.4
10.由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示,延长AH交CD于点P,若,,则小正方形边长GF的长是( )
A. B. C.3 D.
二、填空题
11.如图,在△ABC中,D为BC中点,将△ABD沿AD折叠得到△AED,连接EC,已知BC=6,AD=2,且S△CDE=,则点A到DE的距离为 .
12.如图,E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,连接AC、HE、EC、GA、GF,已知AG⊥GF,AC=2,则AB的长为 .
13.在平面直角坐标系中,如图,,点,点C在y轴上且,连接.现给出以下结论:
①连接,则;
②的周长是一个固定值;
③的最小值为1;
④当取最小值时,.
其中正确的是 (写出所有正确结论的序号)
14.如图,在平面直角坐标系中,点A(0,1),点B为直线y=x上的一个动点,∠ABC=90°,BC=2AB,则OC的最小值为 .
15.已知是直角三角形,连接以为底作直角三角形且是边上的一点,连接和且则长为 .
16.将矩形OABC如图放置,O为坐标原点,若点A(﹣1,2),点B的纵坐标是,则点C的坐标是 .
17.如图,矩形中,,.矩形绕着点A旋转,点B、C、D的对应点分别是点、、,如果点恰好落在对角线上,连接,与交于点E,那么 .
18.如图,正方形ABCD的边长为2,E是AB的中点,连接ED,延长EA至F,使EF=ED.以线段AF为边作正方形AFGH,点H落在AD边上,连接FH并延长,交ED于点M,则的值为 .
三、解答题
19.已知矩形ABCD,点E在AD边上,连接BE、BD,∠BED=2∠BDC,BE=25,BC=32,则CD的长度为 .
20.在正方形ABCD中,P为AB边上一点,将△BCP沿CP折叠,得到△FCP.
(1)如图1,延长PF交AD于E,求证:EF=ED;
(2)如图2,DF,CP的延长线交于点G,求的值.
21.如图,在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿CB向点B方向运动,如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
(1)当t=3秒时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式.
(3)当t为多少秒时,以点C,P,Q为顶点的三角形与△ABC相似?
22.如图1.已知四边形是矩形.点在的延长线上.与相交于点,与相交于点
求证:;
若,求的长;
如图2,连接,求证:.
23.如图,正方形ABCD中,P是对角线AC上的一个动点(不与A、C重合),连结BP,将BP绕点B顺时针旋转到BQ,连结QP交BC于点E,QP延长线与边AD交于点F.
(1)连结CQ,求证:;
(2)若,求的值;
(3)求证:.
24.【操作发现】
如图①,在正方形ABCD中,点N、M分别在边BC、CD上,连结AM、AN、MN.
∠MAN=45°,将△AMD绕点A顺时针旋转90°,点D与点B重合,得到△ABE.易证:△ANM≌△ANE,从而得DM+BN=MN.
【实践探究】
(1)在图①条件下,若CN=3,CM=4,则正方形ABCD的边长是 .
(2)如图②,点M、N分别在边CD、AB上,且BN=DM.点E、F分别在BM、DN上,∠EAF=45°,连接EF,猜想三条线段EF、BE、DF之间满足的数量关系,并说明理由.
【拓展】
(3)如图③,在矩形ABCD中,AB=3,AD=4,点M、N分别在边DC、BC上,连结AM,AN,已知∠MAN=45°,BN=1,求DM的长.
试卷第2页,共2页
试卷第1页,共1页
参考答案:
1.D
【分析】假设直线与∠OAB的平分线交x轴点C,交y轴于D,易求得OA=3,OB=4,AB=5,OD=b,且直线与AB平行,利用角平分线性质可得,再由平行线分线段成比例得即,解得,结合图象,,利用排除法即可得到答案.
【详解】假设直线与∠OAB的平分线交x轴点C,交y轴于D,如图:
∵A(0,3),B(4,0),
∴OA=3,OB=4,AB=5,且直线AB斜率等于,
由直线知OD=b,且直线与AB平行,
∵AC平分∠OAB,
∴,
∵直线与AB平行,
∴即,
解得,
结合图象直线的位置,b的范围为,
利用排除法,
故选D.
【点睛】本题考查了角平分线的性质和平行线分线段成比例,利用假设法和排除法解答是选择题的一种技巧.
2.C
【分析】延长BC交FE的延长线于点H,推出,通过证明,得出,继而得出,再证明,得出,再证明,从而得出答案.
【详解】解:延长BC交FE的延长线于点H,
∵
∴
∴
∴
∵是CD的中点
∴
∴
∴
∴
∴
∴
∴
∵
∴
∵
∴
∴
∵
∴
∵
∴
∴
∴
∴
故选:C.
【点睛】本题考查的知识点是相似三角形的判定及性质,作出辅助线后多次利用相似三角形的性质得出CH、AE的值是解此题的关键.
3.D
【分析】先依据勾股定理求得的长,然后依据翻折的性质可知,故此点在以为圆心,以2为半径的圆上,依据垂线段最短可知当时,点到的距离最短,然后依据题意画出图形,最后,利用相似三角形的性质求解即可.
【详解】解:如图所示:当.
由翻折的性质可知:,.
,
.
由垂线段最短可知此时有最小值.
又为定值,
有最小值.
又,,
.
∴,
∵CF=2,AC=6,BC=8,
∴AF=4,AB==10,
∴即,
∴.
.
故选:.
【点睛】本题考查翻折变换、最短问题、相似三角形的判定和性质、勾股定理.垂线段最短等知识,解题的关键是正确找到点P位置,属于中考常考题型.
4.C
【分析】延长AD、BC交于点E,过点D作DFBE,垂足为F,如图所示,易发现,通过对应边成比例,可求解出DE、CE,再利用即可求出DF、BF.
【详解】延长AD、BC交于点E,过点D作DFBE,垂足为F,如图所示,
,,
,
,
又,
,
设DE=x,CE=y,
,
整理可得关于x,y的二元一次方程组,
,
解得,
,
故选C.
【点睛】利用三角形相似,找到边与边的比例关系,可以求出未知边长,再利用勾股定理即可求解.
5.D
【分析】当点运动到点位置时,,则,当点运动到中点位置时,,即,证明,当在的延长线上时,且,根据相似三角形的性质求得的长,即可求得点的横坐标
【详解】解:根据函数图象可知,当点运动到点位置时,,则,
当点运动到中点位置时,,即,
∴
四边形是矩形
的纵坐标相等,则当在的延长线上时,,,,
,
即
解得,(舍)
即点的坐标为(,2)
故选:D
【点睛】本题考查了动点问题函数图象,相似三角形的性质与判定,从函数图像获取信息是解题的关键.
6.B
【详解】根据相似三角形对应边成比例,由△COB∽△CAO求出CB、AC的关系AC=4CB,从而得到,过点C作CD⊥y轴于点D,然后求出△AOB和△CDB相似,根据相似三角形对应边成比例求出CD=、BD=,再求出OD=,最后写出点C的坐标为(,).
故选:B.
点睛:本题考查了相似三角形的性质,坐标与图形性质,主要利用了相似三角形对应边成比例,求出是解题的关键,也是本题的难点.
7.B
【分析】先计算得出∠CDC'=∠ADA'=∠ADC'=36°,得到点C'在对角线BD上,再证明△BDA∽△BAC',求得BP= C'A= C'B=,进一步计算即可求解.
【详解】解:连接BC',AC',如图:
∵五边形A'B'BCD为正五边形,
∴∠CDA'==108°,
∵菱形ABCD绕点D顺时针旋转得到菱形A'B'C'D,且∠ADC=72°,
∴∠A'DC'=∠ADC=72°,
∴∠CDC'=∠ADA'=108°-72°=36°,
∴∠CDC'=∠ADA'=∠ADC'=36°,
∴点C'在对角线BD上,∠ABC'=36°,
由旋转的性质知AD=AB= DC'=2,
∴∠DC'A=∠DAC'=72°,
∴∠C'AB=36°,
∴C'A= C'B,
设C'A= C'B=x,则BD= x+2,
∵∠BDA=∠BAC'=36°,
∴△BDA∽△BAC',
∴DA:AC'=BD:BA,即2:x=( x+2):2,
整理得:x2+2x-4=0,
解得x=,(负值已舍)
∵∠C'BP=36°,∠BC'P=72°,
∴∠C'PB=72°,
∴BP= C'A= C'B=,
∴AP=3-,
∴,
故选:B.
【点睛】本题考查了正多边的性质,菱形的性质,相似三角形的判定和性质,二次根式的混合运算,解题的关键是学会利用参数构建方程解决问题.
8.A
【分析】画出裁切后的矩形,再利用相似求解即可.
【详解】如图所示,四边形ABQN是裁切后的矩形:
∴,,
∴
∴
∵正方形HFG的面积是24
∴
∴
∴
∴
∴
∴
解得
故选:A.
【点睛】本题考查相似三角形的判定与性质、矩形的性质,解题的关键是正确的画出裁切后拼成的矩形.
9.C
【分析】过点G作GI⊥AB,GH⊥ED',垂足分别为I、H,由折叠的性质可得C′E=5-4=1,在Rt△EFC′中,设FC′=x,则EF=3-x,由勾股定理得:12+(3-x)2=x2,解得:x=,再证明△BC′D'∽△C′GH,设C′H=3m,则GH=4m,C′G=5m,则HD'=GI=AI=4-3m,ID'=5-(4-3m)=1+3m=GH=4m,可得到C′G=5m=5,从而解决问题.
【详解】解:由折叠的性质得,∠AD'E=∠D=90°,AD=AD',
又∵∠DAB=90°,
∴四边形ADED'是矩形,
∵AD=AD',
∴四边形ADED'是正方形,
过点G作GI⊥AB,GH⊥ED',垂足分别为I、H,
∵AD'ED是正方形,
∴AD=DE=ED'=AD'=5,BC=BC′=5,∠C=∠BC′F=90°,FC=FC′,
∴D'B=EC=8-5=3,
在Rt△C′BD'中,C′D'=4,
∴C′E=5-4=1,
在Rt△EFC′中,设FC′=x,则EF=3-x,由勾股定理得:
12+(3-x)2=x2,
解得:x=,
∵∠BC′D'+∠GC′H=90°,∠GC′H+∠C′GH=90°,
∴∠BC′D'=∠C′GH,
又∵∠GHC′=∠BD'C′=90°,
∴△BC′D'∽△C′GH,
∴C′H:GH:C′G=BD':C′D':BC′=3:4:5,
设C′H=3m,则GH=4m,C′G=5m,
∴HD'=GI=AI=4-3m,ID'=5-(4-3m)=1+3m=GH=4m,
解得:m=1,
∴C′G=5m=5,
∴FG=;
故选:C.
【点睛】本题主要考查了矩形的性质,正方形的判定与性质,翻折的性质,勾股定理,相似三角形的判定与性质等知识,作辅助线构造三角形相似是解题的关键.
10.B
【分析】过点E作EM⊥AB于点M,证明△AED∽△HMD,可得, 由MH∥DP,可得,从而可得结论.
【详解】解:∵△ADE≌△DCH≌△CBG≌△BAF,
∴AE=DH,DE=CH,
∵四边形GFEH是正方形,
∴EH=EF=HG=GF,∠HFA=45°=∠EHF,
∵AP⊥HF,
∴∠FAH=∠AFH=45°=∠AHE,
∴AH=FH,AE=HE,
∴AF=2AE,
设AE=a,则AF=DE=2a, 如图过点H作HM⊥AD于M,
∴
∵∠DMH=∠AED=90°,∠ADE=∠MDH,
∴△AED∽△HMD,
∴,
∴,,
∴,
∵AD⊥CD, ∴MH∥DP,
∴ ,
∵AP=10,
∴AH=6,
∴EH==GF,
故选:B.
【点睛】本题考查了正方形的性质,勾股定理,相似三角形的判定和性质,添加恰当辅助线构造相似三角形是解题的关键.
11..
【分析】过点E作EF⊥BC于F,AG⊥DE于G,AH⊥BC于H,由将△ABD沿AD折叠得到△AED,可得,可证,由D为BC中点,BC=6,可求,由S△CDE=,可求,在Rt△EDF中,由勾股定理,可求FC=,在Rt△ECF中,由勾股定理,可证,可得 ,可求即可
【详解】解:过点E作EF⊥BC于F,AG⊥DE于G,AH⊥BC于H,
∵将△ABD沿AD折叠得到△AED,
∴,
∴AD为∠BDE的平分线,
∵EF⊥BC于F,AG⊥DE于G,
∴,
∵D为BC中点,BC=6,
∴,
∵S△CDE=,
∴,
∴,
在Rt△EDF中,由勾股定理,
∴FC=DC-DF=3-,
在Rt△ECF中,由勾股定理,
∵DE=DC,
∴,
由外角性质,,
∴,
,
∴,
∴即,
∴,
∴AG=,
故答案为:.
【点睛】本题考查折叠性质,角平分线性质,三角形面积,勾股定理,相似三角形判定与性质,掌握折叠性质,角平分线性质,三角形面积,勾股定理,相似三角形判定与性质,利用辅助线画出准去图形是解题关键.
12.
【分析】如图,连接BD.由△ADG∽△GCF,设CF=BF=a,CG=DG=b,可得=,推出,可得b=a,在Rt△GCF中,利用勾股定理求出b,即可解决问题;
【详解】如图,连接BD.
∵四边形ABCD是矩形,
∴∠ADC=∠DCB=90°,AC=BD=2,
∵CG=DG,CF=FB,
∴GF=BD=,
∵AG⊥FG,
∴∠AGF=90°,
∴∠DAG+∠AGD=90°,∠AGD+∠CGF=90°,
∴∠DAG=∠CGF,
∴△ADG∽△GCF,
设CF=BF=a,CG=DG=b,
∴=,
∴,
∴b2=2a2,
∵a>0.b>0,
∴b=a,
在Rt△GCF中,3a2=3,
∴a=1,
∴AB=2b=2.
故答案为2.
【点睛】本题考查三角形中位线定理、矩形的性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
13.①③④
【分析】①利用勾股定理计算出AC的长,进行判断;②表示出△OAB的周长即可判断;③利用图形变形,将BC放在三角形中根据三角形的三边关系进行判断;④利用三垂直模型及三角形相似求出OA的长即可.
【详解】解:①∵A(a,0),OA=OC,
∴ACa,
故①正确;
②C△OAB=OA+AB+OB=a+3+2,
∵3﹣2a<3+2,
∴C△OAB不是一个固定值,
故②错误;
③如图,将△OBC绕点O顺时针旋转90°,得到△ODA,
则OB=OD,BC=AD,∠BOD=90°,
∴BD4,
在△ABD中,AD>BD﹣AB,
当B,A,D三点共线时,AD最短,即BC最短,
此时BC=DA﹣AB=4﹣3=1,
故③正确;
④如图,当B,A,D三点共线时,作BE,DF垂直于x轴,垂足为E,F,
则∠OEB=∠DFO=90°,∠1+∠2=90°,
又∠BOD=∠2+∠3=90°,
∴∠1=∠3,
又OB=OD,
∴△BOE≌△ODF(AAS),
设B(x,y),则DF=OE=x,OF=BE=y,且x2+y2=(2)2=8,
由BE⊥x轴,DF⊥x轴得BE∥DF,
∴△ADF∽△ABE,
∴,即,
∴y=3x,
把y=3x代入x2+y2=(2)2=8得,
x2+9x2=8,
解得x=±(负值舍去),
∴y,
由△ADF∽△ABE得,,
∴AE=3AF,
即a﹣x=3(y﹣a),
a﹣x=3y﹣3a,
∴a,
即OA.
故④正确.
故答案为:①③④.
【点睛】本题考查勾股定理,相似以及两点间的距离公式,熟练掌握勾股定理是解题关键.
14.
【分析】分析求OC最小即求AC最小,求AC最小即求AB最小,根据点到直线的距离公式求AB最小,继而代换求出OC最小.
【详解】连接OC,在△AOC中,
OC
故求OC最短,即求AC最短
由题意知:∠ABC=,BC=2AB且点A(0,1),
设AB=m,BC=2m,AC= m
根据点到直线的距离可知,m最小= .
此时AB⊥直线y=x,点C在直线上
∴BC=
作BD⊥OA与点D,
在△ABD和△BOD中
∴△DOB∽△OBA
∴
又∵AB=m=
∴OB=
∴OC=
故答案为.
【点睛】本题主要考查了点到直线的距离公式及三角形相似的性质,正确掌握点到直线的距离公式及三角形相似的性质是解题的关键.
15.
【分析】将线段绕点顺时针旋转,得到线段,连接,HE,利用证明,得,,则,即可解决问题.
【详解】解:将线段绕点顺时针旋转,得到线段,连接,HE,
是等腰直角三角形,
∴∠HBD=45°
∵∠FBD=45°
∴点B、F、H共线
又是等腰直角三角形,
,,,
,
,,
,
,
,
,
,
,
故答案为:.
【点睛】本题主要考查了等腰直角三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质等知识,解题的关键是作辅助线构造全等三角形.
16.(3,)
【分析】过点A作AD⊥x轴,垂足为D,过点B作BF⊥x轴,垂足为F,过点C作CG⊥x轴,垂足为G,过点B作BE⊥CG,交GC的延长线于点E,通过证明△ADO≌△CEB,△ADO∽△OGC即可.
【详解】过点A作AD⊥x轴,垂足为D,过点B作BF⊥x轴,垂足为F,过点C作CG⊥x轴,垂足为G,过点B作BE⊥CG,交GC的延长线于点E,
∴四边形BFGE是矩形,∠ADO=∠CBE=90°,
∴BF=EG,
∵四边形OABC是矩形,
∴OA=CB,∠BCO=90°,
∴∠AOD=90°-∠COG=∠GCO=90°-∠BCE=∠CBE,
∴△ADO≌△CEB,△ADO∽△OGC,
∴AD=CE,,
∵点A(﹣1,2),点B的纵坐标是,
∴AD=CE=2,BF=EG=,CG=EG-CE=-2=,
∴,
解得OG=3,
故点C的坐标为(3,),
故答案为:(3,).
【点睛】本题考查了矩形的性质,三角形全等的判定和性质,三角形相似的判定和性质,坐标与线段的关系,熟练掌握矩形的性质,三角形的全等与系数是解题的关键.
17.
【分析】过A点作AF⊥BD,交BD于点F,利用勾股定理求出BD=5,在根据是矩形ABD的面积求出AF,进而可求出,进而求出,再证明,即有,DE可求.
【详解】过A点作AF⊥BD,交BD于点F,如图,
∵矩形中AB=3,BC=AD=4,∠BAC=90°,
∴,
∵,
∴,
∴,
根据旋转可知:,,,
∵,
∴,即,
∴,
根据旋转可知:,,,
∴根据两个等腰三角形中顶角相等,则其底角也相等,即,
∵,
∴,
∵,,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:.
【点睛】本题考查了旋转的性质,矩形的性质,勾股定理,等腰三角形的性质,相似三角形的判定与性质,求出是解答本题的关键.
18.
【分析】过点M作MN⊥AD于点N,根据勾股定理可得DE=EF=,根据四边形AFGH是正方形,可得AF=AH=EF﹣AE=,根据,可得△DMN∽△DEA,所以,即,即可设MN=NH=x,则DN=2x,DM=,再根据DN+NH=AD﹣AH,列式,求出x的值,进而可以解决问题.
【详解】解:如图,过点M作MN⊥AD于点N,
∵正方形ABCD的边长为2,E是AB的中点,
∴AD=AB=2,AE=1,∠EAD=90°,
∴,
∵四边形AFGH是正方形,
∴AF=AH=EF﹣AE=,
∵∠AHF=∠NHM=45°,
∴MN=NH,
∵,
∴△DMN∽△DEA,
∴,
∴,
设MN=NH=x,
则DN=2x,DM=,
∴DN+NH=AD﹣AH,
∴,
∴,
∴,
∴,
故答案为:.
【点睛】此题考查了正方形的性质和三角形相似的知识,解决本题的关键是找到相似三角形得出线段之间的关系.
19.24
【分析】过E作EF⊥BD于F,根据矩形的性质得到∠C=∠ADC=90°,于是得到∠ADB+∠BDC=90°,根据已知条件推出180°-∠AEB=2(90°-∠ADB),得到∠AEB=2∠EDB,根据等腰三角形的性质得到BF=BD,由平行线的性质得到∠ADB=∠DBC,等量代换得到∠EBF=∠DBC,推出△EBF∽△DBC,根据相似三角形的性质,求得BD=40,由勾股定理即可得到结论.
【详解】过作于,
∵四边形是矩形,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∴.
故答案为:24.
【点睛】本题考查了矩形的性质,相似三角形的判定和性质,平行线的性质,外角的性质,正确的作出辅助线构造相似三角形是解题的关键.
20.(1)证明见解析(2)
【分析】(1)连接CE,通过全等三角形的判定,得到Rt△CFE≌Rt△CDE,进而得出结论;
(2)连接BG、BF、BD,作CH⊥DF,垂足为H.依据△CFG≌△CBG,可得GF=GB,进而得出△GBF是等腰直角三角形,故BF=BG.再判定△BGA∽△FBD,即可得到.
【详解】(1)如图1,连接CE,
∵四边形ABCD是正方形,
∴BC=CD,∠B=∠D=90°.
∵△PBC和△FPC关于PC对称,
∴BC=CF,∠B=∠PFC=90°.
∴∠EFC=90°.
∴∠EFC=∠D=90°,CF=CD.
∵CE=CE,
∴Rt△EFC≌Rt△DFC(HL).
∴EF=ED.
(2)如图2,连接BG、BF、BD,作CH⊥DF,垂足为H.
∵四边形ABCD是正方形,
∴BC=CD.
∵CH⊥DF,
∴∠HCF=,
∵△PBC和△FPC关于PC对称,
∴BC=CF,∠FCG=∠BCG.
∴EB⊥CG.
又∵CG=CG,
∴△CFG≌△CBG.
∴GF=GB.
∵∠HCF=,∠FCG=∠BCG=,
∴∠HCK==45°.
∴∠PFH=135°.
∴∠GFB=45°.
∴∠GBF=45°.
∴△GBF是等腰直角三角形.
∴.
∵∠ABD=45°,
∴∠GBA=∠FBD.
∵,
∴△BGA∽△FBD.
∴.
【点睛】本题主要考查了全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,等腰直角三角形的判定与性质的综合运用,解决问题的关键是作辅助线构造等腰直角三角形,全等三角形以及相似三角形,利用相似三角形的对应边成比例得出结论.
21.(1)10cm;(2);(3)t=3或t=
【分析】(1)在Rt△CPQ中,当t=3秒,可知CP、CQ的长,运用勾股定理可将PQ的长求出;
(2)由点P,点Q的运动速度和运动时间,又知AC,BC的长,可将CP、CQ用含t的表达式求出,代入直角三角形面积公式=CP×CQ求解;
(3)应分两种情况:当Rt△CPQ∽Rt△CAB时,根据,可将时间t求出;当Rt△CPQ∽Rt△CBA时,根据,可求出时间t.
【详解】由题意得AP=4t,CQ=2t,则CP=20﹣4t,
(1)当t=3秒时,CP=20﹣4t=8cm,CQ=2t=6cm,
由勾股定理得PQ=;
(2)由题意得AP=4t,CQ=2t,则CP=20﹣4t,
因此Rt△CPQ的面积为S=;
(3)分两种情况:
①当Rt△CPQ∽Rt△CAB时,
,即,
解得:t=3秒;
②当Rt△CPQ∽Rt△CBA时,
,即,
解得:t=秒.
因此t=3秒或t=秒时,以点C、P、Q为顶点的三角形与△ABC相似
【点睛】本题主要考查了相似三角形性质以及勾股定理的运用,在解第三问时应分两种情况进行求解防止漏解或错解,注意方程思想与分类讨论思想的应用是解此题的关键.
22.(1)见解析;(2);(3)见解析
【分析】(1)由矩形的形及已知证得△EAF≌△DAB,则有∠E=∠ADB,进而证得∠EGB=90 即可证得结论;
(2)设AE=x,利用矩形性质知AF∥BC,则有,进而得到x的方程,解之即可;
(3)在EF上截取EH=DG,进而证明△EHA≌△DGA,得到∠EAH=∠DAG,AH=AG,则证得△HAG为等腰直角三角形,即可得证结论.
【详解】(1)∵四边形ABCD是矩形,
∴∠BAD=∠EAD=90 ,AO=BC,AD∥BC,
在△EAF和△DAB,
,
∴△EAF≌△DAB(SAS),
∴∠E=∠BDA,
∵∠BDA+∠ABD=90 ,
∴∠E+∠ABD=90 ,
∴∠EGB=90 ,
∴BG⊥EC;
(2)设AE=x,则EB=1+x,BC=AD=AE=x,
∵AF∥BC,∠E=∠E,
∴△EAF∽△EBC,
∴,又AF=AB=1,
∴即,
解得:,(舍去)
即AE=;
(3)在EG上截取EH=DG,连接AH,
在△EAH和△DAG,
,
∴△EAH≌△DAG(SAS),
∴∠EAH=∠DAG,AH=AG,
∵∠EAH+∠DAH=90 ,
∴∠DAG+∠DAH=90 ,
∴∠HAG=90 ,
∴△GAH是等腰直角三角形,
∴即,
∴GH=AG,
∵GH=EG-EH=EG-DG,
∴.
【点睛】本题主要考查了矩形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、直角定义、相似三角形的判定与性质、解一元二次方程等知识,涉及知识面广,解答的关键是认真审题,提取相关信息,利用截长补短等解题方法确定解题思路,进而推理、探究、发现和计算.
23.(1)见解析;(2) ;(3)见解析
【分析】(1)由旋转知△PBQ为等腰直角三角形,得到PB=QB,∠PBQ=90°,进而证明△APB≌△CQB即可;
(2)设AP=x,则AC=4x,PC=3x,由(1)知CQ=AP=x,又△ABC为等腰直角三角形,所以BC=,PQ=,再证明△BQE∽△BCQ,由此求出BE,进而求出CE:BC的值;
(3)在CE上截取CG,并使CG=FA,证明△PFA≌△QGC,进而得到PF=QG,然后再证明∠QGE=∠QEG即可得到QG=EQ,进而求解.
【详解】解:∵四边形ABCD为正方形,
∴AB=BC,∠ABC=90°,
∵BP绕点B顺时针旋转到BQ,
∴BP=BQ,∠PBQ=90°,
∴∠ABC-∠PBC=∠PBQ-∠PBC,
∴∠ABP=∠CBQ,
在△APB和△CQB中,
,
∴△APB≌△CQB(SAS),
∴AP=CQ.
(2) 设AP=x,则AC=4x,PC=3x,由(1)知CQ=AP=x,
△ABC为等腰直角三角形,∴BC=,
在Rt△PCQ中,由勾股定理有:,
且△PBQ为等腰直角三角形,
∴,
又∠BCQ=∠BAP=45°,∠BQE=45°,
∴∠BCQ=∠BQE=45°,且∠CBQ=∠CBQ,
∴△BQE∽△BCQ,
∴,代入数据:,
∴BE=,∴CE=BC-BE=,
∴,
故答案为:.
(3) 在CE上截取CG,并使CG=FA,如图所示:
∵∠FAP=∠GCQ=45°,
且由(1)知AP=CQ,且截取CG=FA,
故有△PFA≌△QGC(SAS),
∴PF=QG,∠PFA=∠CGQ,
又∵∠DFP=180°-∠PFA,∠QGE=180°-∠CGQ,
∴∠DFP=∠QGE,
∵DABC,
∴∠DFP=∠CEQ,
∴∠QGE=∠CEQ,
∴△QGE为等腰三角形,
∴GQ=QE,
故PF=QE.
【点睛】本题考查了正方形的性质、旋转的性质、三角形全等的判定和性质、相似三角形判定和性质的综合,具有一定的综合性,本题第(3)问关键是能想到在CE上截取CG,并使CG=FA这条辅助线.
24.(1)6;(2),见解析;(3)2
【分析】(1)根据旋转的性质证明△ABE≌△ADM得到BE=DM,又由∠ABE=∠D=90°,AE=AM,∠BAE=∠DAM,证出∠EAM=90°,得出∠MAN=∠EAN,再证明△AMN≌△EAN(SAS),得出MN=EN最后证出MN=BN+DM.在Rt△CMN中,由勾股定理计算即可得到正方形的边长;
(2 )先根据旋转的性质证明△AEG≌△AEF(SAS),再证明∠GBE=90°,再根据勾股定理即可得到;
(3)在AB上截取AP,在BC上截取BQ,使AP=AB=BQ=3,连结PQ交AM于点R,得到ABQP为正方形,再根据操作发现以及勾股定理即可得到答案;
【详解】(1)(1)解:∵四边形ABCD是正方形,
∴AB=CD=AD,∠BAD=∠C=∠D=90°,
由旋转得:△ABE≌△ADM,
∴BE=DM,∠ABE=∠D=90°,AE=AM,∠BAE=∠DAM,
∴∠BAE+∠BAM=∠DAM+∠BAM=∠BAD=90°,
即∠EAM=90°,
∵∠MAN=45°,
∴∠EAN=90°-45°=45°,
∴∠MAN=∠EAN,
在△AMN和△EAN中,
∴△AMN≌△EAN(SAS),
∴MN=EN.
∵EN=BE+BN=DM+BN,
∴MN=BN+DM.
在Rt△CMN中,
,
则BN+DM=5,
设正方形ABCD的边长为x,则BN=BC-CN=x-3,DM=CD-CM=x-4,
∴x-3+x-4=5,
解得:x=6,
即正方形ABCD的边长是6;
故答案为:6;
(2)数量关系为:,证明如下:
将△AFD绕点A顺时针旋转90°,点D与点B重合,得到△ABG,连结EG.
由旋转的性质得到:AF=AG,
又∵∠EAF=45°,
∴,
且AE=AE,
∴△AEG≌△AEF(SAS),
从而得EG=EF.(全等三角形对应边相等),
又∵BN=DM,BN∥DM,
∴四边形DMBN是平行四边形(一组对边平行且相等的四边形是平行四边形),
∴DN∥BM,
∴ (两直线平行,同位角相等),
∵,
∴(等量替换),
即:∠GBE=90°,
则,
∴;
(3)在AD上截取AP,在BC上截取BQ,使AP=AB=BQ=3,连结PQ交AM于点R,
易证ABQP为正方形,
由操作与发现知:PR+BN=RN.
设PR=x,则RQ=3﹣x,RN=1+x,QN=3-1=2
在Rt△QRN中,由勾股定理得:
,
即
解得:x=,
∴PR=
∵PQ∥DC,
∴△APR∽△ADM,
∴ (相似三角形对应边成比例)
∴
∴DM=2;
【点睛】本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、勾股定理、相似三角形的判定与性质等知识;本题综合性强,有一定难度,证明三角形全等和由勾股定理得出方程是解题的关键.
答案第1页,共2页
答案第1页,共2页
