1.4.2三角形三条角平分线的性质 教学课件(共25张PPT) 2022—2023学年北师大版数学八年级下册
文档属性
| 名称 | 1.4.2三角形三条角平分线的性质 教学课件(共25张PPT) 2022—2023学年北师大版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 776.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 20:05:03 | ||
图片预览






文档简介
(共25张PPT)
1.4.2 三角形三条角平分线的性质
回顾旧知
角平分线的性质定理:
角平分线上的点到这个角两边的距离相等。
角平分线的判定定理:
在一个角的内部,到角的两边距离相等的点在这个角的角平分线上。
模块1
讲作业
模块2
上新课
模块3
做练习
模块4
课堂小结
大家玩过折纸吗?请拿出你准备好的一个三角形,我们来折一折:
1、请折出三角形的三个角的角平分线;
情境引入
2、请问这三条角平分线能否通过尺规作图作出来呢?
A
B
C
3、请问这三条角平分线有什么位置关系?
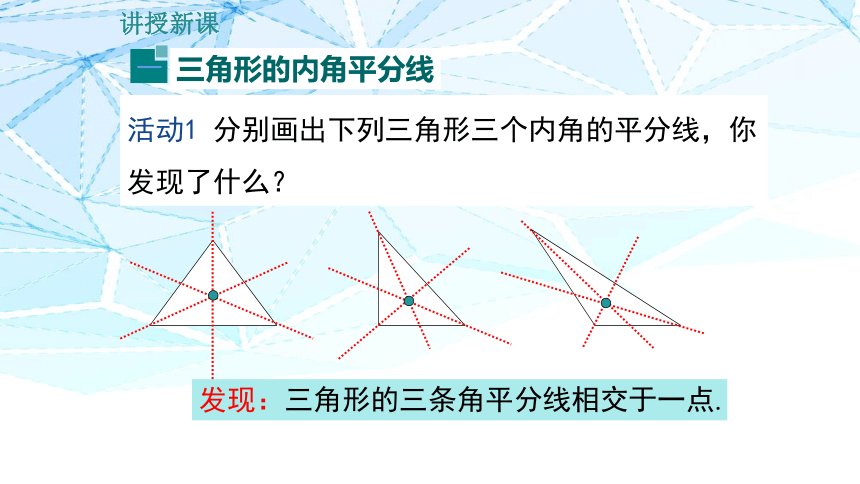
活动1 分别画出下列三角形三个内角的平分线,你发现了什么?
三角形的内角平分线
一
发现:三角形的三条角平分线相交于一点.
讲授新课
活动2 分别过此交点作三角形三边的垂线,每组垂线段,你猜想一下他们有什么数量关系?
猜想:过此交点作三角形三边的垂线段相等.
发现:1、三角形的三条角平分线相交于一点.
2、过此交点作三角形三边的垂线段相等.
你能证明你的猜想吗?
联想:对于第一个结论,我们能否借鉴之前证明三角形三条垂直平分线交于一点的证明方法吗?
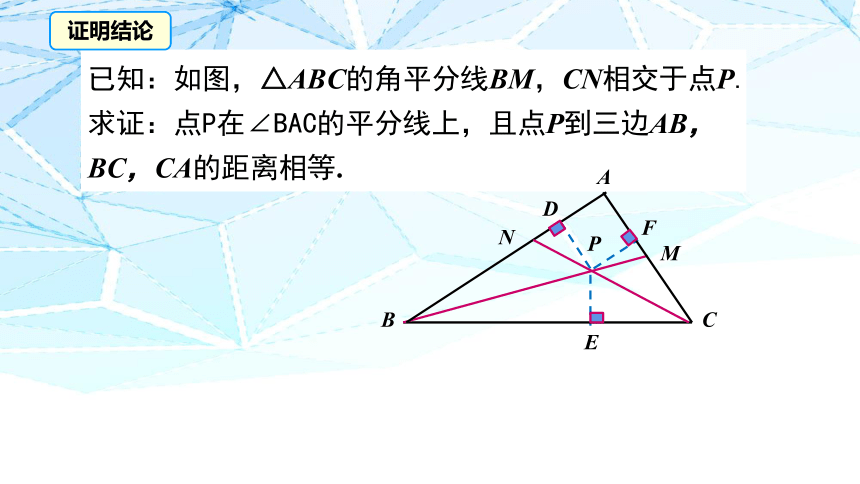
已知:如图,△ABC的角平分线BM,CN相交于点P.
求证:点P在∠BAC的平分线上,且点P到三边AB,BC,CA的距离相等.
证明结论
D
E
F
A
B
C
P
N
M
D
E
F
A
B
C
P
N
M
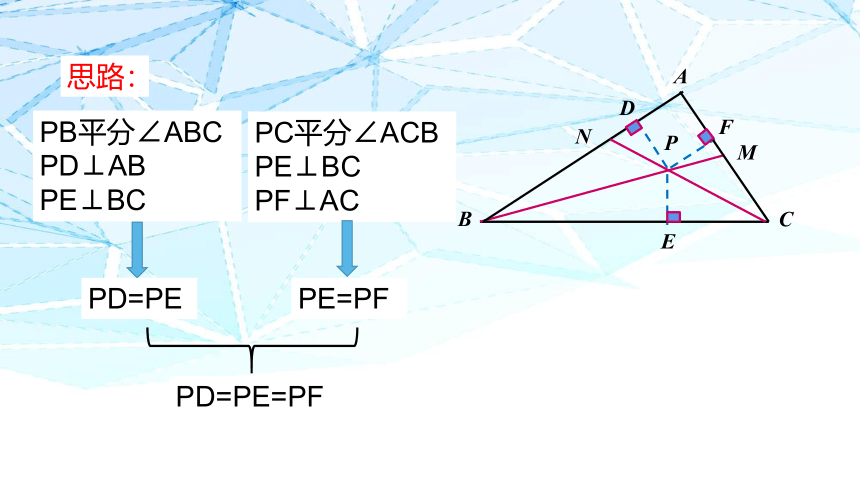
思路:
PB平分∠ABC
PD⊥AB
PE⊥BC
PD=PE
PC平分∠ACB
PE⊥BC
PF⊥AC
PE=PF
PD=PE=PF
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,
点P在BM上,PD⊥AB,PE⊥BC
∴PD=PE(角平分线上的点到这个角的两边的距离相等).
同理PE=PF(角平分线上的点到这个角的两边的距离相等).
∴PD=PF=PE(等量代换)
∴点P在∠BAC的平分线上(在一个角的内部,且到角两边距离相等的点,在这个角的平分线上)
∴点P到三边AB,BC,CA的距离相等.
D
E
F
A
B
C
P
N
M
归纳总结
三角形的三条角平分线相交于一点,并且这一点到三角形三条边的距离相等。
这个点叫三角形的内心
(即三角形内切圆的圆心)
应用格式:
∵点P是∠ABC,∠ACB的平分线的交点,PD⊥AB,PE⊥BC,PF⊥AC
∴点P在∠BAC的角平分线上,
且PD=PF=PE(三角形的三条角平分线
交于一点,并且这一点到三条边的距离相等)
D
E
F
A
B
C
P
N
M
三角形中垂线与角平分线的区别 三边垂直平分线 三条角平分线
三角形 锐角三角形
钝角三角形 直角三角形 交点性质
交于三角形内一点
交于三角形外一点
交于斜边的中点
到三角形三个顶点的距离相等
交于三角形内一点
到三角形三边的距离相等
议一议
练习1. 如图,在△ABC中.AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.(1)已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD.
练一练
解:(1)∵AD是△ABC的角平分线,DC⊥AC,DE⊥AB(已知)
∴DE=CD=4cm(角平分线上的点到这个角的两条边的距离相等)
又∵AC=BC,∠C=90°
∴∠B=∠BAC=45°(等腰直角三角形的两底角均为45°)
∴BE=DE=4cm.(等腰直角三角形的两直角边相等)
在等腰直角三角形BDE中,
由勾股定理得,BD=4 cm,
∴AC=BC=CD+BD=4+4 (cm)
(2)∵AD是△ABC的角平分线,DC⊥AC,DE⊥AB,
∴∠ACE=∠AED=90°(三角形内角和180°)在Rt△ACD 和Rt△AED中,
AD=AD
CD=DE
∴Rt△ACD≌Rt△AED(HL)∴AC=AE(全等三角形对应边相等)
又∵BE=DE=CD ∴AB=AE+BE=AC+CD.
M
E
N
A
B
C
P
O
D
(2)若△ABC的周长为32,求△ABC的面积.
练习2. 如图,在△ABC中,AP平分∠BAC,BD平分∠ABC,AP,BD交于点O,过点O作OM⊥AC,若OM=4.
(1)点O到△ABC三边的距离和为_________;
12
M
E
N
A
B
C
P
O
D
解:(2)连接OC.
从这道题中,你能归纳出一个求面积的公式吗?
练习3. 如图,PB,PC分别是△ABC的外角平分线,且相交于点P,求证:点P在∠BAC的平分线上
M
Q
N
解:过点P作PM⊥AB于点M,作PN⊥AC于点N,作PQ⊥BC于点Q
∵PB,PC分别是△ABC的外角平分线, PM⊥AB,PN⊥AC,PQ⊥BC(已知)
∴PM=PQ,PN=PQ(角平分线上的点到
这个角两边的距离相等)
∴PM=PN(等量代换)
又∵PM⊥AB,PN⊥AC,点P在∠BAC的内部
∴点P在∠BAC的角平分线上(在一个角的内部,到这个角两边距离相等的点在这个角的角平分线上)
M
Q
N
拓展思维
练习4.如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个货物中转站。
(1)要求它到l1、l2这两条公路的距离相等, 那么如何选择货物中转站的位置?
(2)要求它到这三条公路的距离都相等, 那么如何选择货物中转站的位置?
P1
P2
P3
P4
l1
l2
l3
课后总结: 这节课你的收获是什么?
总结
三角形中垂线与角平分线的区别 三边垂直平分线 三条角平分线
三角形 锐角三角形
钝角三角形 直角三角形 交点性质
交于三角形内一点
交于三角形外一点
交于斜边的中点
到三角形三个顶点的距离相等
交于三角形内一点
到三角形三边的距离相等
1.4.2 三角形三条角平分线的性质
回顾旧知
角平分线的性质定理:
角平分线上的点到这个角两边的距离相等。
角平分线的判定定理:
在一个角的内部,到角的两边距离相等的点在这个角的角平分线上。
模块1
讲作业
模块2
上新课
模块3
做练习
模块4
课堂小结
大家玩过折纸吗?请拿出你准备好的一个三角形,我们来折一折:
1、请折出三角形的三个角的角平分线;
情境引入
2、请问这三条角平分线能否通过尺规作图作出来呢?
A
B
C
3、请问这三条角平分线有什么位置关系?
活动1 分别画出下列三角形三个内角的平分线,你发现了什么?
三角形的内角平分线
一
发现:三角形的三条角平分线相交于一点.
讲授新课
活动2 分别过此交点作三角形三边的垂线,每组垂线段,你猜想一下他们有什么数量关系?
猜想:过此交点作三角形三边的垂线段相等.
发现:1、三角形的三条角平分线相交于一点.
2、过此交点作三角形三边的垂线段相等.
你能证明你的猜想吗?
联想:对于第一个结论,我们能否借鉴之前证明三角形三条垂直平分线交于一点的证明方法吗?
已知:如图,△ABC的角平分线BM,CN相交于点P.
求证:点P在∠BAC的平分线上,且点P到三边AB,BC,CA的距离相等.
证明结论
D
E
F
A
B
C
P
N
M
D
E
F
A
B
C
P
N
M
思路:
PB平分∠ABC
PD⊥AB
PE⊥BC
PD=PE
PC平分∠ACB
PE⊥BC
PF⊥AC
PE=PF
PD=PE=PF
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,
点P在BM上,PD⊥AB,PE⊥BC
∴PD=PE(角平分线上的点到这个角的两边的距离相等).
同理PE=PF(角平分线上的点到这个角的两边的距离相等).
∴PD=PF=PE(等量代换)
∴点P在∠BAC的平分线上(在一个角的内部,且到角两边距离相等的点,在这个角的平分线上)
∴点P到三边AB,BC,CA的距离相等.
D
E
F
A
B
C
P
N
M
归纳总结
三角形的三条角平分线相交于一点,并且这一点到三角形三条边的距离相等。
这个点叫三角形的内心
(即三角形内切圆的圆心)
应用格式:
∵点P是∠ABC,∠ACB的平分线的交点,PD⊥AB,PE⊥BC,PF⊥AC
∴点P在∠BAC的角平分线上,
且PD=PF=PE(三角形的三条角平分线
交于一点,并且这一点到三条边的距离相等)
D
E
F
A
B
C
P
N
M
三角形中垂线与角平分线的区别 三边垂直平分线 三条角平分线
三角形 锐角三角形
钝角三角形 直角三角形 交点性质
交于三角形内一点
交于三角形外一点
交于斜边的中点
到三角形三个顶点的距离相等
交于三角形内一点
到三角形三边的距离相等
议一议
练习1. 如图,在△ABC中.AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.(1)已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD.
练一练
解:(1)∵AD是△ABC的角平分线,DC⊥AC,DE⊥AB(已知)
∴DE=CD=4cm(角平分线上的点到这个角的两条边的距离相等)
又∵AC=BC,∠C=90°
∴∠B=∠BAC=45°(等腰直角三角形的两底角均为45°)
∴BE=DE=4cm.(等腰直角三角形的两直角边相等)
在等腰直角三角形BDE中,
由勾股定理得,BD=4 cm,
∴AC=BC=CD+BD=4+4 (cm)
(2)∵AD是△ABC的角平分线,DC⊥AC,DE⊥AB,
∴∠ACE=∠AED=90°(三角形内角和180°)在Rt△ACD 和Rt△AED中,
AD=AD
CD=DE
∴Rt△ACD≌Rt△AED(HL)∴AC=AE(全等三角形对应边相等)
又∵BE=DE=CD ∴AB=AE+BE=AC+CD.
M
E
N
A
B
C
P
O
D
(2)若△ABC的周长为32,求△ABC的面积.
练习2. 如图,在△ABC中,AP平分∠BAC,BD平分∠ABC,AP,BD交于点O,过点O作OM⊥AC,若OM=4.
(1)点O到△ABC三边的距离和为_________;
12
M
E
N
A
B
C
P
O
D
解:(2)连接OC.
从这道题中,你能归纳出一个求面积的公式吗?
练习3. 如图,PB,PC分别是△ABC的外角平分线,且相交于点P,求证:点P在∠BAC的平分线上
M
Q
N
解:过点P作PM⊥AB于点M,作PN⊥AC于点N,作PQ⊥BC于点Q
∵PB,PC分别是△ABC的外角平分线, PM⊥AB,PN⊥AC,PQ⊥BC(已知)
∴PM=PQ,PN=PQ(角平分线上的点到
这个角两边的距离相等)
∴PM=PN(等量代换)
又∵PM⊥AB,PN⊥AC,点P在∠BAC的内部
∴点P在∠BAC的角平分线上(在一个角的内部,到这个角两边距离相等的点在这个角的角平分线上)
M
Q
N
拓展思维
练习4.如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个货物中转站。
(1)要求它到l1、l2这两条公路的距离相等, 那么如何选择货物中转站的位置?
(2)要求它到这三条公路的距离都相等, 那么如何选择货物中转站的位置?
P1
P2
P3
P4
l1
l2
l3
课后总结: 这节课你的收获是什么?
总结
三角形中垂线与角平分线的区别 三边垂直平分线 三条角平分线
三角形 锐角三角形
钝角三角形 直角三角形 交点性质
交于三角形内一点
交于三角形外一点
交于斜边的中点
到三角形三个顶点的距离相等
交于三角形内一点
到三角形三边的距离相等
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
