第十二章全等三角形 单元测试卷(含答案) 2023--2024学年人教版数学八年级上册
文档属性
| 名称 | 第十二章全等三角形 单元测试卷(含答案) 2023--2024学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 214.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 20:11:20 | ||
图片预览



文档简介
第十二章全等三角形 单元测试卷
一.选择题(共10小题)
1.如图,点D在AB上,点E在AC上,且∠AEB=∠ADC,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.∠B=∠C C.BE=CD D.AB=AC
2.如图,射线OC平分∠AOB,点D、Q分别在射线OC、OB上,若OQ=4,△ODQ的面积为10,过点D作DP⊥OA于点P,则DP的长为( )
A.10 B.5 C.4 D.3
3.如图,工人师傅设计了一种测零件内径AB的卡钳,卡钳交叉点O为AA'、BB'的中点,只要量出A'B'的长度,就可以知道该零件内径AB的长度.依据的数学基本事实是( )
A.两边及其夹角分别相等的两个三角形全等
B.两角及其夹边分别相等的两个三角形全等
C.两条直线被一组平行线所截,所得的对应线段成比例
D.两点之间线段最短
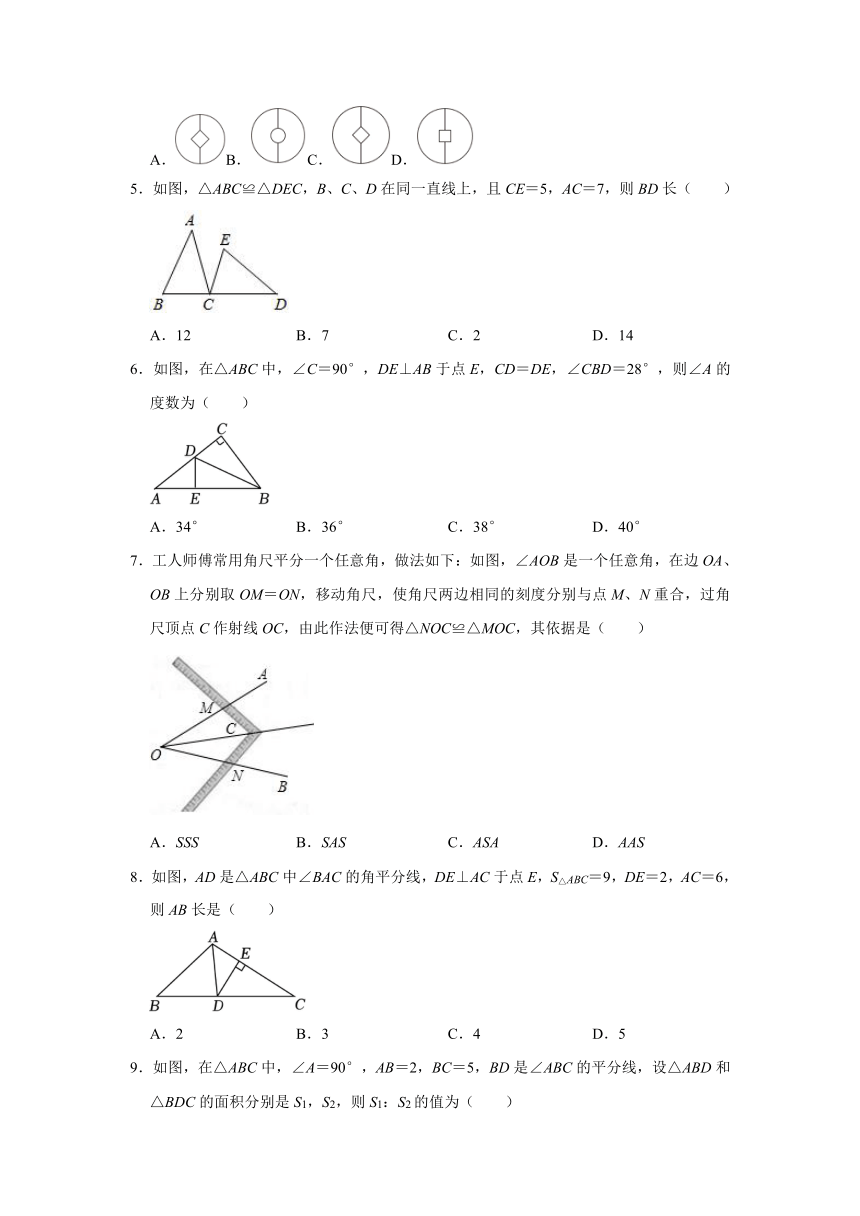
4.下列选项中的图形与如图的图形是全等形的是( )
A.B.C.D.
5.如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( )
A.12 B.7 C.2 D.14
6.如图,在△ABC中,∠C=90°,DE⊥AB于点E,CD=DE,∠CBD=28°,则∠A的度数为( )
A.34° B.36° C.38° D.40°
7.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
8.如图,AD是△ABC中∠BAC的角平分线,DE⊥AC于点E,S△ABC=9,DE=2,AC=6,则AB长是( )
A.2 B.3 C.4 D.5
9.如图,在△ABC中,∠A=90°,AB=2,BC=5,BD是∠ABC的平分线,设△ABD和△BDC的面积分别是S1,S2,则S1:S2的值为( )
A.5:2 B.2:5 C.1:2 D.1:5
10.如图,△ABC中,∠ACF、∠EAC的角平分线CP、AP交于点P,延长BA、BC,PM⊥BE,PN⊥BF.则下列结论中正确的个数( )
①BP平分∠ABC;②∠ABC+2∠APC=180°;③∠CAB=2∠CPB;④S△PAC=S△MAP+S△NCP.
A.1个 B.2个 C.3个 D.4个
二.填空题(共5小题)
11.如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是27cm2,AB=8cm,BC=10cm,则DE= cm.
12.如图,在△ABC中,∠ACB=60°,CD平分∠ACB,点E,F分别在边AC,BC上,△ADE 与△BDF 的面积之和为S.若∠EDF=120°,AD=3,BD=2,则S为 .
13.如图,已知∠NBC=∠MEF,NB=ME,若以“SAS”为依据判定△NBC≌△MEF,还要添加的条件为 .
14.如图,AB=8cm,AC=BD=6cm,∠CAB=∠DBA=60°,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).设点Q的运动速度为xcm/s,若使得△ACP与△BPQ全等,x的值为 .
15.如图,三角形ABC中,BD平分∠ABC,AD垂直于BD,三角形BCD的面积为45,三角形ADC的面积为20,则三角形ABD的面积等于 .
三.解答题(共4小题)
16.如图:AB∥CD,AD∥BC,求证:AB=CD.
证明:∵AB∥CD.
∴∠ABD=∠CDB( ),
∵AD∥BC,
∴∠ADB=∠CBD( ),
在△ABD和△CDB中,
∵,
∴△ABD≌△CDB( ),
∴AB=CD( ).
17.如图,点C、F、E、B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,写出CD与AB之间的关系,并证明你的结论.
18.如图,B是AD的中点,BC∥DE,BC=DE.求证:∠C=∠E.
19.【阅读理解】
课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB的理由是 .
A.SSS B.SAS C.AAS D.HL
(2)求得AD的取值范围是 .
A.6<AD<8 B.6≤AD≤8 C.1<AD<7 D.1≤AD≤7
【感悟】
解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
【问题解决】
如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.求证:AC=BF.
参考答案
1--10BBACA AABBD
11.3
12.
13.BC=EF
14.1.5或1.
15.25
16.证明:∵AB∥CD.
∴∠ABD=∠CDB(两直线平行,内错角相等),
∵AD∥BC,
∴∠ADB=∠CBD(两直线平行,内错角相等),
在△ABD和△CDB中,
,
∴△ABD≌△CDB(ASA),
∴AB=CD(全等三角形的对应边相等).
17.解:CD=AB,CD∥AB,理由如下:
∵CE=BF,
∴CE﹣EF=BF﹣EF,
∴CF=BE,
在△CFD和△BEA中,
,
∴△CFD≌△BEA(SAS),
∴CD=AB,∠C=∠B,
∴CD∥AB.
18.证明:∵B是AD的中点,
∴AB=BD,
∵BC∥DE,
∴∠ABC=∠D,
在△ABC和△BDE中,
,
∴△ABC≌△BDE(SAS),
∴∠C=∠E.
19.(1)解:∵在△ADC和△EDB中
,
∴△ADC≌△EDB(SAS),
故选B;
(2)解:∵由(1)知:△ADC≌△EDB,
∴BE=AC=6,AE=2AD,
∵在△ABE中,AB=8,由三角形三边关系定理得:8﹣6<2AD<8+6,
∴1<AD<7,
故选C.
(3)证明:
延长AD到M,使AD=DM,连接BM,
∵AD是△ABC中线,
∴CD=BD,
∵在△ADC和△MDB中
∴△ADC≌△MDB,
∴BM=AC,∠CAD=∠M,
∵AE=EF,
∴∠CAD=∠AFE,
∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M,
∴BF=BM=AC,
即AC=BF.
一.选择题(共10小题)
1.如图,点D在AB上,点E在AC上,且∠AEB=∠ADC,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.∠B=∠C C.BE=CD D.AB=AC
2.如图,射线OC平分∠AOB,点D、Q分别在射线OC、OB上,若OQ=4,△ODQ的面积为10,过点D作DP⊥OA于点P,则DP的长为( )
A.10 B.5 C.4 D.3
3.如图,工人师傅设计了一种测零件内径AB的卡钳,卡钳交叉点O为AA'、BB'的中点,只要量出A'B'的长度,就可以知道该零件内径AB的长度.依据的数学基本事实是( )
A.两边及其夹角分别相等的两个三角形全等
B.两角及其夹边分别相等的两个三角形全等
C.两条直线被一组平行线所截,所得的对应线段成比例
D.两点之间线段最短
4.下列选项中的图形与如图的图形是全等形的是( )
A.B.C.D.
5.如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( )
A.12 B.7 C.2 D.14
6.如图,在△ABC中,∠C=90°,DE⊥AB于点E,CD=DE,∠CBD=28°,则∠A的度数为( )
A.34° B.36° C.38° D.40°
7.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
8.如图,AD是△ABC中∠BAC的角平分线,DE⊥AC于点E,S△ABC=9,DE=2,AC=6,则AB长是( )
A.2 B.3 C.4 D.5
9.如图,在△ABC中,∠A=90°,AB=2,BC=5,BD是∠ABC的平分线,设△ABD和△BDC的面积分别是S1,S2,则S1:S2的值为( )
A.5:2 B.2:5 C.1:2 D.1:5
10.如图,△ABC中,∠ACF、∠EAC的角平分线CP、AP交于点P,延长BA、BC,PM⊥BE,PN⊥BF.则下列结论中正确的个数( )
①BP平分∠ABC;②∠ABC+2∠APC=180°;③∠CAB=2∠CPB;④S△PAC=S△MAP+S△NCP.
A.1个 B.2个 C.3个 D.4个
二.填空题(共5小题)
11.如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是27cm2,AB=8cm,BC=10cm,则DE= cm.
12.如图,在△ABC中,∠ACB=60°,CD平分∠ACB,点E,F分别在边AC,BC上,△ADE 与△BDF 的面积之和为S.若∠EDF=120°,AD=3,BD=2,则S为 .
13.如图,已知∠NBC=∠MEF,NB=ME,若以“SAS”为依据判定△NBC≌△MEF,还要添加的条件为 .
14.如图,AB=8cm,AC=BD=6cm,∠CAB=∠DBA=60°,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).设点Q的运动速度为xcm/s,若使得△ACP与△BPQ全等,x的值为 .
15.如图,三角形ABC中,BD平分∠ABC,AD垂直于BD,三角形BCD的面积为45,三角形ADC的面积为20,则三角形ABD的面积等于 .
三.解答题(共4小题)
16.如图:AB∥CD,AD∥BC,求证:AB=CD.
证明:∵AB∥CD.
∴∠ABD=∠CDB( ),
∵AD∥BC,
∴∠ADB=∠CBD( ),
在△ABD和△CDB中,
∵,
∴△ABD≌△CDB( ),
∴AB=CD( ).
17.如图,点C、F、E、B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,写出CD与AB之间的关系,并证明你的结论.
18.如图,B是AD的中点,BC∥DE,BC=DE.求证:∠C=∠E.
19.【阅读理解】
课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB的理由是 .
A.SSS B.SAS C.AAS D.HL
(2)求得AD的取值范围是 .
A.6<AD<8 B.6≤AD≤8 C.1<AD<7 D.1≤AD≤7
【感悟】
解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
【问题解决】
如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.求证:AC=BF.
参考答案
1--10BBACA AABBD
11.3
12.
13.BC=EF
14.1.5或1.
15.25
16.证明:∵AB∥CD.
∴∠ABD=∠CDB(两直线平行,内错角相等),
∵AD∥BC,
∴∠ADB=∠CBD(两直线平行,内错角相等),
在△ABD和△CDB中,
,
∴△ABD≌△CDB(ASA),
∴AB=CD(全等三角形的对应边相等).
17.解:CD=AB,CD∥AB,理由如下:
∵CE=BF,
∴CE﹣EF=BF﹣EF,
∴CF=BE,
在△CFD和△BEA中,
,
∴△CFD≌△BEA(SAS),
∴CD=AB,∠C=∠B,
∴CD∥AB.
18.证明:∵B是AD的中点,
∴AB=BD,
∵BC∥DE,
∴∠ABC=∠D,
在△ABC和△BDE中,
,
∴△ABC≌△BDE(SAS),
∴∠C=∠E.
19.(1)解:∵在△ADC和△EDB中
,
∴△ADC≌△EDB(SAS),
故选B;
(2)解:∵由(1)知:△ADC≌△EDB,
∴BE=AC=6,AE=2AD,
∵在△ABE中,AB=8,由三角形三边关系定理得:8﹣6<2AD<8+6,
∴1<AD<7,
故选C.
(3)证明:
延长AD到M,使AD=DM,连接BM,
∵AD是△ABC中线,
∴CD=BD,
∵在△ADC和△MDB中
∴△ADC≌△MDB,
∴BM=AC,∠CAD=∠M,
∵AE=EF,
∴∠CAD=∠AFE,
∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M,
∴BF=BM=AC,
即AC=BF.
