专题29.3投影与视图 全章复习与巩固 巩固篇 专项练习(含解析)2023-2024学年九年级数学下册人教版专项讲练
文档属性
| 名称 | 专题29.3投影与视图 全章复习与巩固 巩固篇 专项练习(含解析)2023-2024学年九年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 805.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 18:50:49 | ||
图片预览

文档简介
专题29.3 投影与视图(全章复习与巩固)
(巩固篇)(专项练习)
一、单选题
1.下列现象中,属于中心投影的是( )
A.白天旗杆的影子 B.阳光下广告牌的影子
C.灯光下演员的影子 D.中午小明跑步的影子
2.一个矩形木框在太阳光的照射下,在地面上的投影不可能是( )
A. B. C. D.
3.如图所示是两根标杆在地面上的影子,根据这些投影,在灯光下形成的影子是( )
A.①和② B.②和④ C.③和④ D.②和③
4.若线段CD是线段AB的正投影,则AB与CD的大小关系为( )
A.AB>CD B.AB<CD C.AB=CD D.AB≥CD
5.当你在笔直的公路上乘车由A至E的过程中(如图所示),发现路边有两栋建筑物,那么不能看到较高建筑物PD的路段是( )
A.AB B.BC C.CD D.DE
6.如图是由五个相同的小正方体搭成的一个几何体,它的主视图是( )
A. B. C. D.
7.如图是由大小相同的小正方体搭成的几何体从上向下看得到的平面图形,小正方形中的数字表示该位置上小正方体的个数,则从左向右看得到的平面图形是( )
A. B. C. D.
8.由一些大小相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体的小正方体不同摆放方式共有( )
A.6种 B.5种 C.4种 D.3种
9.图①是由五个完全相同的小正方体组成的立体图形,将图①中的一个小正方体改变位置后得到图②,则图①与图②的三视图不相同的是( )
A.主视图 B.俯视图
C.左视图 D.主视图、俯视图和左视图都不同
10.如图,树在路灯O的照射下形成投影,已知树的高度,树影,树与路灯O的水平距离,则路灯高的长是( )
A. B. C. D.
二、填空题
11.如图,由五个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的主视图和左视图的面积之和是 .
12.在同一时刻两根垂直于水平地面的木竿在太阳光下的影子如图所示,其中木竿,它的影子,木竿的影子有一部分落在了墙上,则木竿的长度为 .
13.一个几何体由若干大小相同的小正方体搭成,如图分别是从它的正面、上面看到的形状图,若组成这个几何体的小正方体最少需要m个,最多需要n个,则m﹣n= .
14.在数学活动课上,老师带领数学小组测量大树AB的高度.如图,数学小组发现大树离教学楼5 m,大树的影子有一部分落在地面上,还有一部分落在教学楼的墙上,墙上的影子CD长为2 m,已知此时高1.4 m的竹竿在水平地面上的影子长1 m,那么这棵大树高 m.
15.一个圆柱的三种视图如图所示.则这个圆柱的体积为 .
16.如图,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5m,在旋转过程中,影长的最大值为5m,最小值3m,且影长最大时,木杆与光线垂直,则路灯EF的高度为 m.
17.如图,小军、小珠之间的距离为2.7 m,他们在同一盏路灯下的影长分别为1.8 m,1.5 m,已知小军、小珠的身高分别为1.8 m,1.5 m,则路灯的高为 m.
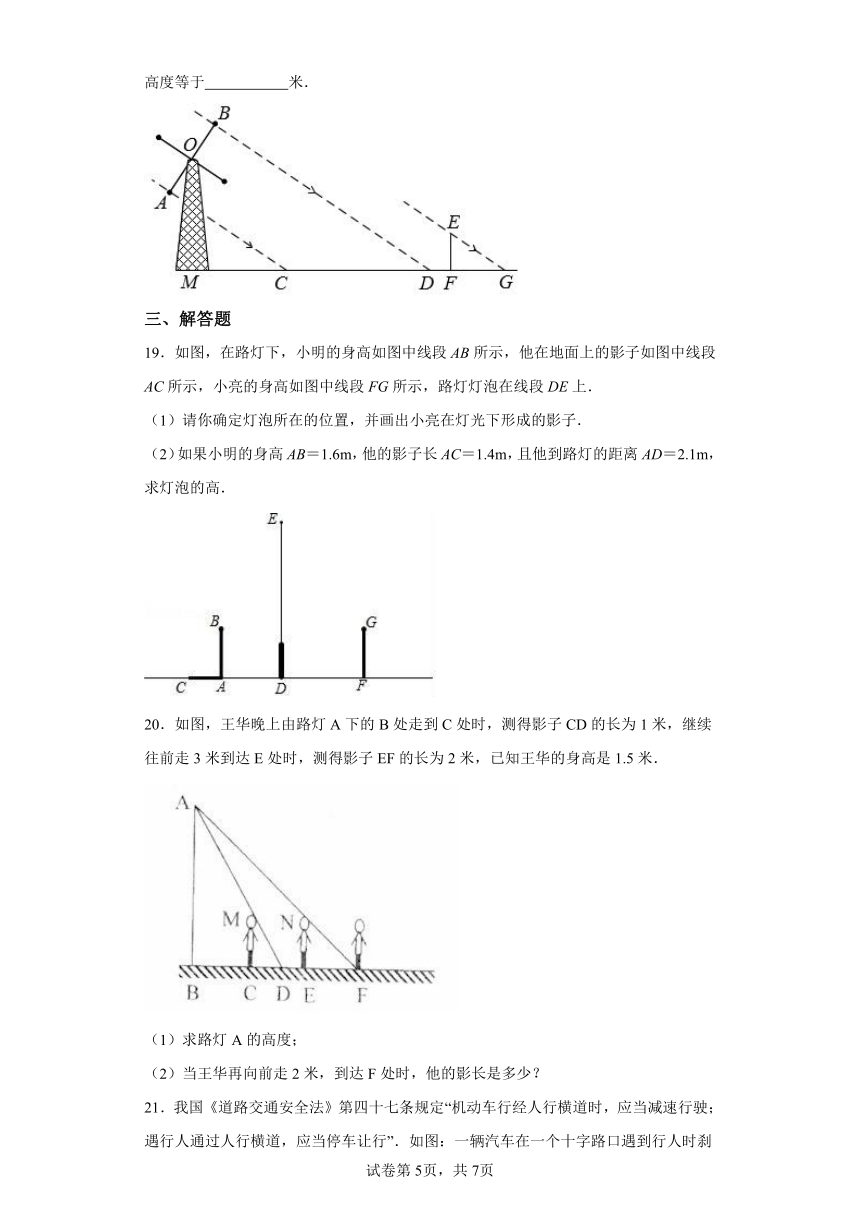
18.如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片,此时各叶片影子在点M右侧成线段,测得,垂直于地面的木棒与影子的比为2∶3,则点O,M之间的距离等于 米.转动时,叶片外端离地面的最大高度等于 米.
三、解答题
19.如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
20.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米.
(1)求路灯A的高度;
(2)当王华再向前走2米,到达F处时,他的影长是多少?
21.我国《道路交通安全法》第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行”.如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少?
22.如图,这是一个由小正方体搭成的几何体从上面看得到的平面图形,小正方形中的数字表示该位置的小正方体的个数.请你画出从它的正面和左面看得到的平面图形.
23.由几个相同的边长为1的小立方块搭成的几何体的从上面看如下图,格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸中分别画出这个几何体的从正面和左面看到的图形.
(2)根据以上图形;这个组合几何体的表面积为_________个平方单位.(包括底面积)
24.如图几何体是由若干棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),观察该图,探究其中的规律.
(1)第1个几何体中只有2个面涂色的小立方体共有______个;第2个几何体中只有2个面涂色的小立方体共有______个;第3个几何体中只有2个面涂色的小立方体共有______个.
(2)求出第10个几何体中只有2个面涂色的小立方体的块数.
(3)求出前100个几何体中只有2个面涂色的小立方体的块数的和.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据平行投影和中心投影的定义对各选项进行判断.
【详解】解:A.白天旗杆的影子为平行投影,所以A选项不合题意;
B.阳光下广告牌的影子为平行投影,所以B选项不合题意;
C.灯光下演员的影子为中心投影,所以C选项符合题意;
D.中午小明跑步的影子为平行投影,所以D选项不合题意.
故选:C.
【点睛】本题考查了中心投影:由同一点(点光源)发出的光线形成的投影叫做中心投影.如物体在灯光的照射下形成的影子就是中心投影.也考查了平行投影.
2.B
【分析】根据平行投影的性质求解可得.
【详解】解:一张矩形纸片在太阳光线的照射下,形成影子不可能是等边三角形,
故选:B.
【点睛】本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.
3.D
【分析】根据光线相交的是灯光光线,光线平行的不是灯光光线逐个判断.
【详解】连接并延长每个标杆影子的末端与标杆的顶端,射线相交的是灯光下形成的影子,不相交的不是灯光下形成的影子.
故选:D.
【点睛】本题考查了中心投影,熟练掌握中心投影的定义是解决此类问题的关键.
4.D
【分析】根据正投影的定义和性质解答可得.
【详解】若线段AB平行于投影面,则AB=CD,
若线段AB不平行于投影面,则AB>CD,
则AB≥CD,
故答案选:D.
【点睛】本题考查了平行投影的知识点,解题的关键是熟练的掌握正投影的定义和性质.
5.B
【分析】若不能看到建筑物PD,则PD位于此线段的盲区内,可据此进行判断.
【详解】由图知:当乘车在BC段行驶时,建筑物PD位于自己的盲区内,因此看不到建筑物PD的路段是BC段.
故选B.
【点睛】理解视点、视角和盲区的定义是解答此类题目的关键.
6.D
【分析】主视图就是正面看去所得图形,左起第一列为一个小正方形,第二列两个小正方形.
【详解】解:主视图从左往右,每一列的小正方形数量分别为1、2,
故选择:D.
【点睛】本题考查了主视图的概念,能准确看出主视图是解题的关键.
7.A
【分析】根据左视图的定义解答可得.
【详解】解:由俯视图知,该几何体共3行2列,
第1列自左向右有3个正方体,第2列有1个正方体,
其左视图如下所示:
故选A.
【点睛】此题考查了由三视图判断几何体,做这类题时要借助三种视图表示物体的特点,从主视图上弄清物体的上下和左右形状;从俯视图上弄清物体的左右和前后形状;从左视图上弄清楚物体的上下和前后形状,综合分析,合理猜想,结合生活经验描绘出草图后,再检验是否符合题意,理解上述内容是解题的关键.
8.B
【分析】根据三视图的定义,画出图形即可.
【详解】解:根据主视图和左视图,搭成该几何体的小正方体不同摆放方式如下,
共有5种不同摆放方式,
故选;B.
【点睛】本题考查三视图,解题的关键是理解三视图的定义,对于一般的立体图要通过仔细观察和想象,再画它的图形.
9.A
【分析】先分别确定①、②的三视图,然后再对比即可解答.
【详解】解:①的主视图是第一层三个小正方形,第二层左边一个小正方形;左视图是第一层两个小正方形,第二层左边一个小正方形;俯视图是第一层中间一个小正方形,第二层三个小正方形;
②的主视图是第一层三个小正方形,第二层中间一个小正方形;左视图是第一层两个小正方形,第二层左边一个小正方形;俯视图是第一层中间一个小正方形,第二层三个小正方形;
所以将图①中的一个小正方体改变位置后,俯视图和左视图均没有发生改变,只有主视图发生改变,
故选:A.
【点睛】本题考查了三视图的知识,解决此类图的关键是由三视图得到相应的立体图形.从正面看到的图是正视图,从上面看到的图形是俯视图,从左面看到的图形是左视图.
10.C
【分析】根据相似三角形的判定与性质直接求解即可.
【详解】解:根据题意可知,
,,
,
,即,解得m,
路灯高的长是m,
故选:C.
【点睛】本题考查中心投影以及相似三角形的应用,测量不能到达顶部的物体的高度,通常利用相似三角形的性质即相似三角形的对应边成比例和“在同一时刻物高与影长的比相等”的原理解决.
11.7
【分析】根据从左面看得到的图形是左视图,从前面看的到的视图是主视图,再根据面积求出面积的和即可.
【详解】解:该几何体的主视图的面积为1×1×4=4,左视图的面积是1×1×3=3,
所以该几何体的主视图和左视图的面积之和是3+4=7,
故答案为:7.
【点睛】本题考查了简单几何体的三视图,确定左视图、主视图是解题关键.
12.3m
【分析】过N点作ND⊥PQ于D,根据同一时刻物高与影长成正比求出QD的影长,再根据此影长列出比例式求解即可.
【详解】解:如图:过N点作ND⊥PQ于D,
∴四边形DPMN是矩形
∴DN=PM,PD=MN
∴,
又∵AB=2.5,BC=2,DN=PM=1.6,NM=1,
∴QD===2(m),
∴PQ=QD+DP=QD+NM=2+1=3(m).
故答案为3m.
【点睛】本题考查了平行投影;在运用投影的知识解决实际问题时,要能够从实际问题中抽象出简单的数学模型是解答本题的关键.
13.﹣4
【分析】由主视图和俯视图,判断最多的正方体的个数即可解决问题.
【详解】解:由主视图和俯视图可确定所需正方体个数多时的俯视图为:
最多的小正方形个数时:
∴n=1+2+2+2+3+3=13,
最少的小正方形个数时:
∴m=1+1+1+2+1+3=9,
∴m-n=9-13=﹣4,
故答案为:﹣4
【点睛】此题主要考查了由三视图判断几何体,根据主视图和俯视图画出所需正方体个数最多和最少的俯视图是关键.
14.9
【分析】过点D作DE⊥AB于E,则四边形BCDE是矩形,得BE=CD=2m,DE=BC=5m,再根据同一时刻,物高与影长成正比,可得,代入DE,即可求出AE长,即可由AB=AE+BE求解.
【详解】解:如图,过点D作DE⊥AB于E,
由题意,得AB⊥BC,DC⊥BC,
∵DE⊥AB,
∴四边形BCDE是矩形,
∴BE=CD=2m,DE=BC=5m,
由题意,得,
∴,
∴AE=7
∴AB=AE+BE=7+2=9(m),
答:这棵大树高为9m,
故答案为:9.
【点睛】本题考查解直角三角形的应用,熟练掌握同一时刻,物高与影长成正比是解题的关键.
15.24π
【分析】根据主视图确定圆柱的高为6,根据俯视图确定圆的直径为4即半径为2,利用公式计算即可.
【详解】∵
∴圆柱的高为6,圆的直径为4即半径为2,
∴圆柱的体积为==24π,
故答案为:24π.
【点睛】本题考查了圆柱的三视图,圆柱的体积,熟练读懂三视图,确定圆柱的高和直径是解题的关键.
16.7.5
【分析】根据木杆旋转时影子的长度变化确定木杆AB的长,然后利用相似三角形的性质求得EF的高度即可.
【详解】解:当旋转到达地面时,为最短影长,等于AB,
∵最小值3m,
∴AB=3m,
∵影长最大时,木杆与光线垂直,
即AC=5m,
∴BC=4 m,
又可得△CAB∽△CFE,
∴
∵AE=5m,
∴
解得:EF=7.5m
故答案为7.5.
【点睛】本题考查了中心投影和相似三角形的判定及性质的知识,解题的关键是根据影子的变化确定木杆的长度.
17.3
【详解】解:如图,∵CD∥AB∥MN,
∴△ABE∽△CDE,△ABF∽△MNF,
∴,
即,
解得:AB=3m,
故答案为:3
18. 10
【分析】过点O作AC、BD的平行线,交CD于H,过点O作水平线OJ交BD于点J,过点B作BI⊥OJ,垂足为I,延长MO,使得OK=OB,求出CH的长度,根据,求出OM的长度,证明,得出,,求出IJ、BI、OI的长度,用勾股定理求出OB的长,即可算出所求长度.
【详解】如图,过点O作AC、BD的平行线,交CD于H,过点O作水平线OJ交BD于点J,过点B作BI⊥OJ,垂足为I,延长MO,使得OK=OB,
由题意可知,点O是AB的中点,
∵,
∴点H是CD的中点,
∵,
∴,
∴,
又∵由题意可知:,
∴,解得,
∴点O、M之间的距离等于,
∵BI⊥OJ,
∴,
∵由题意可知:,
又∵,
∴,
∴,
∴,
∴,,
∵,
∴四边形OHDJ是平行四边形,
∴,
∵,
∴,,,
∵在中,由勾股定理得:,
∴,
∴,
∴,
∴叶片外端离地面的最大高度等于,
故答案为:10,.
【点睛】本题主要考查了投影和相似的应用,及勾股定理和平行四边形的判定与性质,正确作出辅助线是解答本题的关键.
19.(1)画图见解析;(2)DE=4
【分析】(1)连接CB延长CB交DE于O,点O即为所求.连接OG,延长OG交DF于H.线段FH即为所求.
(2)根据,可得 ,即可推出DO=4m.
【详解】(1)解:如图,点O为灯泡所在的位置,线段FH为小亮在灯光下形成的影子.
(2)解:由已知可得,,
∴,
∴OD=4m,
∴灯泡的高为4m.
【点睛】本题考查中心投影、解题的关键是正确画出图形,记住物长与影长的比的定值,属于基础题,中考常考题型.
20.(1)路灯A有6米高(2)王华的影子长米.
【详解】试题分析:22. 解:(1)由题可知AB//MC//NE,
∴,而MC=NE
∴
∵CD=1米,EF=2米,BF=BD+4,∴BD=4米,∴AB==6米
所以路灯A有6米高
(2) 依题意,设影长为x,则解得米
答:王华的影子长米.
考点:相似三角形性质
点评:本题难度较低,主要考查学生对相似三角形性质解决实际生活问题的能力.为中考常考题型,要求学生牢固掌握解题技巧.
21.0.7米
【分析】直接利用已知得出∠BAC=∠BCA,则BC=AB,再得出BF的长,求出x的值即可.
【详解】解:如图所示:延长AB,
∵CDAB,
∴∠CAB=30°,∠CBF=60°,
∴∠BCA=60°﹣30°=30°,即∠BAC=∠BCA,
∴BC=AB=3m,
在Rt△BCF中,BC=3m,∠CBF=60°,
∴BF=BC=1.5m,
故x=BF﹣EF=1.5﹣0.8=0.7(m),
答:这时汽车车头与斑马线的距离x是0.7m.
【点睛】考查了含30度角的直角三角形,正确得出BF的长是解题关键.
22.见解析
【分析】根据几何体的三视图的性质作图即可.
【详解】如图所示,即为所求.
【点睛】本题考查了几何体三视图的问题,掌握几何体三视图的性质是解题的关键.
23.(1)见解析
(2)24
【分析】(1)从正面看有2列,每列小正方形数目分别为2,3;从左面看有2列,每列小正方形数目分别为3,1;
(2)上面共有3个小正方形,下面共有3个小正方形;左面共有4个小正方形,右面共有4个正方形;前面共有5个小正方形,后面共有5个正方形,继而可得出表面积.
【详解】(1)解:从正面看有2列,每列小正方形数目分别为2,3;从左面看有2列,每列小正方形数目分别为3,1,
图形分别如下:
(2).
∴这个组合几何体的表面积为个平方单位.
【点睛】此题考查了简单几何体的三视图及几何体的表面积的计算,解答本题的关键是掌握三视图的观察方法,在计算表面积时容易出错,要一个面一个面的进行查找,避免遗漏.
24.(1)4,12,20
(2)第10个几何体中只有2个面涂色的小立方体的块数共有76个
(3)前100个几何体中只有2个面涂色的小立方体的个数的和为40000个
【分析】(1)第1个几何体中最底层的4个角的小立方体只有2个面涂色;第2个几何体中只有2个面涂色的小立方体共有3×4=12(个);第3个几何体中只有2个面涂色的小立方体共有5×4=20(个);
(2)根据所给图形中只有2个面涂色的小立方体的块数得到第n个几何体中只有2个面涂色的小立方体的块数与4的倍数的关系即可;
(3)根据(2)得到的规律,进行计算即可.
【详解】(1)解:观察图形可得第1个几何体中最底层的4个角的小立方体只有2个面涂色;
第2个几何体中只有2个面涂色的小立方体共有3×4=12(个);
第3个几何体中只有2个面涂色的小立方体共有5×4=20(个).
故答案为:4,12,20;
(2)解:观察图形可知:图①中,只有2个面涂色的小立方体共有4个;
图②中,只有2个面涂色的小立方体共有12个;
图③中,只有2个面涂色的小立方体共有20个.
4,12,20都是4的倍数,可分别写成4×1,4×3,4×5的形式,
因此,第n个图中两面涂色的小立方体的块数共有:4(2n﹣1)=8n﹣4,
则第10个几何体中只有2个面涂色的小立方体的块数共有8×10﹣4=76(个);
(3)解:(8×1﹣4)+(8×2﹣4)+(8×3﹣4)+(8×4﹣4)+(8×5﹣4)+…+(8×100﹣4)
=8(1+2+3+4+…+100)﹣100×4
=40000(个).
故前100个几何体中只有2个面涂色的小立方体的个数的和为40000个.
【点睛】本题考查了认识立体图形,图形的变化规律.得到所求块数与4的倍数的关系是解决本题的关键.
个数的和为40000个.
答案第1页,共2页
答案第1页,共2页
(巩固篇)(专项练习)
一、单选题
1.下列现象中,属于中心投影的是( )
A.白天旗杆的影子 B.阳光下广告牌的影子
C.灯光下演员的影子 D.中午小明跑步的影子
2.一个矩形木框在太阳光的照射下,在地面上的投影不可能是( )
A. B. C. D.
3.如图所示是两根标杆在地面上的影子,根据这些投影,在灯光下形成的影子是( )
A.①和② B.②和④ C.③和④ D.②和③
4.若线段CD是线段AB的正投影,则AB与CD的大小关系为( )
A.AB>CD B.AB<CD C.AB=CD D.AB≥CD
5.当你在笔直的公路上乘车由A至E的过程中(如图所示),发现路边有两栋建筑物,那么不能看到较高建筑物PD的路段是( )
A.AB B.BC C.CD D.DE
6.如图是由五个相同的小正方体搭成的一个几何体,它的主视图是( )
A. B. C. D.
7.如图是由大小相同的小正方体搭成的几何体从上向下看得到的平面图形,小正方形中的数字表示该位置上小正方体的个数,则从左向右看得到的平面图形是( )
A. B. C. D.
8.由一些大小相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体的小正方体不同摆放方式共有( )
A.6种 B.5种 C.4种 D.3种
9.图①是由五个完全相同的小正方体组成的立体图形,将图①中的一个小正方体改变位置后得到图②,则图①与图②的三视图不相同的是( )
A.主视图 B.俯视图
C.左视图 D.主视图、俯视图和左视图都不同
10.如图,树在路灯O的照射下形成投影,已知树的高度,树影,树与路灯O的水平距离,则路灯高的长是( )
A. B. C. D.
二、填空题
11.如图,由五个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的主视图和左视图的面积之和是 .
12.在同一时刻两根垂直于水平地面的木竿在太阳光下的影子如图所示,其中木竿,它的影子,木竿的影子有一部分落在了墙上,则木竿的长度为 .
13.一个几何体由若干大小相同的小正方体搭成,如图分别是从它的正面、上面看到的形状图,若组成这个几何体的小正方体最少需要m个,最多需要n个,则m﹣n= .
14.在数学活动课上,老师带领数学小组测量大树AB的高度.如图,数学小组发现大树离教学楼5 m,大树的影子有一部分落在地面上,还有一部分落在教学楼的墙上,墙上的影子CD长为2 m,已知此时高1.4 m的竹竿在水平地面上的影子长1 m,那么这棵大树高 m.
15.一个圆柱的三种视图如图所示.则这个圆柱的体积为 .
16.如图,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5m,在旋转过程中,影长的最大值为5m,最小值3m,且影长最大时,木杆与光线垂直,则路灯EF的高度为 m.
17.如图,小军、小珠之间的距离为2.7 m,他们在同一盏路灯下的影长分别为1.8 m,1.5 m,已知小军、小珠的身高分别为1.8 m,1.5 m,则路灯的高为 m.
18.如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片,此时各叶片影子在点M右侧成线段,测得,垂直于地面的木棒与影子的比为2∶3,则点O,M之间的距离等于 米.转动时,叶片外端离地面的最大高度等于 米.
三、解答题
19.如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
20.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米.
(1)求路灯A的高度;
(2)当王华再向前走2米,到达F处时,他的影长是多少?
21.我国《道路交通安全法》第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行”.如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少?
22.如图,这是一个由小正方体搭成的几何体从上面看得到的平面图形,小正方形中的数字表示该位置的小正方体的个数.请你画出从它的正面和左面看得到的平面图形.
23.由几个相同的边长为1的小立方块搭成的几何体的从上面看如下图,格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸中分别画出这个几何体的从正面和左面看到的图形.
(2)根据以上图形;这个组合几何体的表面积为_________个平方单位.(包括底面积)
24.如图几何体是由若干棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),观察该图,探究其中的规律.
(1)第1个几何体中只有2个面涂色的小立方体共有______个;第2个几何体中只有2个面涂色的小立方体共有______个;第3个几何体中只有2个面涂色的小立方体共有______个.
(2)求出第10个几何体中只有2个面涂色的小立方体的块数.
(3)求出前100个几何体中只有2个面涂色的小立方体的块数的和.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据平行投影和中心投影的定义对各选项进行判断.
【详解】解:A.白天旗杆的影子为平行投影,所以A选项不合题意;
B.阳光下广告牌的影子为平行投影,所以B选项不合题意;
C.灯光下演员的影子为中心投影,所以C选项符合题意;
D.中午小明跑步的影子为平行投影,所以D选项不合题意.
故选:C.
【点睛】本题考查了中心投影:由同一点(点光源)发出的光线形成的投影叫做中心投影.如物体在灯光的照射下形成的影子就是中心投影.也考查了平行投影.
2.B
【分析】根据平行投影的性质求解可得.
【详解】解:一张矩形纸片在太阳光线的照射下,形成影子不可能是等边三角形,
故选:B.
【点睛】本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.
3.D
【分析】根据光线相交的是灯光光线,光线平行的不是灯光光线逐个判断.
【详解】连接并延长每个标杆影子的末端与标杆的顶端,射线相交的是灯光下形成的影子,不相交的不是灯光下形成的影子.
故选:D.
【点睛】本题考查了中心投影,熟练掌握中心投影的定义是解决此类问题的关键.
4.D
【分析】根据正投影的定义和性质解答可得.
【详解】若线段AB平行于投影面,则AB=CD,
若线段AB不平行于投影面,则AB>CD,
则AB≥CD,
故答案选:D.
【点睛】本题考查了平行投影的知识点,解题的关键是熟练的掌握正投影的定义和性质.
5.B
【分析】若不能看到建筑物PD,则PD位于此线段的盲区内,可据此进行判断.
【详解】由图知:当乘车在BC段行驶时,建筑物PD位于自己的盲区内,因此看不到建筑物PD的路段是BC段.
故选B.
【点睛】理解视点、视角和盲区的定义是解答此类题目的关键.
6.D
【分析】主视图就是正面看去所得图形,左起第一列为一个小正方形,第二列两个小正方形.
【详解】解:主视图从左往右,每一列的小正方形数量分别为1、2,
故选择:D.
【点睛】本题考查了主视图的概念,能准确看出主视图是解题的关键.
7.A
【分析】根据左视图的定义解答可得.
【详解】解:由俯视图知,该几何体共3行2列,
第1列自左向右有3个正方体,第2列有1个正方体,
其左视图如下所示:
故选A.
【点睛】此题考查了由三视图判断几何体,做这类题时要借助三种视图表示物体的特点,从主视图上弄清物体的上下和左右形状;从俯视图上弄清物体的左右和前后形状;从左视图上弄清楚物体的上下和前后形状,综合分析,合理猜想,结合生活经验描绘出草图后,再检验是否符合题意,理解上述内容是解题的关键.
8.B
【分析】根据三视图的定义,画出图形即可.
【详解】解:根据主视图和左视图,搭成该几何体的小正方体不同摆放方式如下,
共有5种不同摆放方式,
故选;B.
【点睛】本题考查三视图,解题的关键是理解三视图的定义,对于一般的立体图要通过仔细观察和想象,再画它的图形.
9.A
【分析】先分别确定①、②的三视图,然后再对比即可解答.
【详解】解:①的主视图是第一层三个小正方形,第二层左边一个小正方形;左视图是第一层两个小正方形,第二层左边一个小正方形;俯视图是第一层中间一个小正方形,第二层三个小正方形;
②的主视图是第一层三个小正方形,第二层中间一个小正方形;左视图是第一层两个小正方形,第二层左边一个小正方形;俯视图是第一层中间一个小正方形,第二层三个小正方形;
所以将图①中的一个小正方体改变位置后,俯视图和左视图均没有发生改变,只有主视图发生改变,
故选:A.
【点睛】本题考查了三视图的知识,解决此类图的关键是由三视图得到相应的立体图形.从正面看到的图是正视图,从上面看到的图形是俯视图,从左面看到的图形是左视图.
10.C
【分析】根据相似三角形的判定与性质直接求解即可.
【详解】解:根据题意可知,
,,
,
,即,解得m,
路灯高的长是m,
故选:C.
【点睛】本题考查中心投影以及相似三角形的应用,测量不能到达顶部的物体的高度,通常利用相似三角形的性质即相似三角形的对应边成比例和“在同一时刻物高与影长的比相等”的原理解决.
11.7
【分析】根据从左面看得到的图形是左视图,从前面看的到的视图是主视图,再根据面积求出面积的和即可.
【详解】解:该几何体的主视图的面积为1×1×4=4,左视图的面积是1×1×3=3,
所以该几何体的主视图和左视图的面积之和是3+4=7,
故答案为:7.
【点睛】本题考查了简单几何体的三视图,确定左视图、主视图是解题关键.
12.3m
【分析】过N点作ND⊥PQ于D,根据同一时刻物高与影长成正比求出QD的影长,再根据此影长列出比例式求解即可.
【详解】解:如图:过N点作ND⊥PQ于D,
∴四边形DPMN是矩形
∴DN=PM,PD=MN
∴,
又∵AB=2.5,BC=2,DN=PM=1.6,NM=1,
∴QD===2(m),
∴PQ=QD+DP=QD+NM=2+1=3(m).
故答案为3m.
【点睛】本题考查了平行投影;在运用投影的知识解决实际问题时,要能够从实际问题中抽象出简单的数学模型是解答本题的关键.
13.﹣4
【分析】由主视图和俯视图,判断最多的正方体的个数即可解决问题.
【详解】解:由主视图和俯视图可确定所需正方体个数多时的俯视图为:
最多的小正方形个数时:
∴n=1+2+2+2+3+3=13,
最少的小正方形个数时:
∴m=1+1+1+2+1+3=9,
∴m-n=9-13=﹣4,
故答案为:﹣4
【点睛】此题主要考查了由三视图判断几何体,根据主视图和俯视图画出所需正方体个数最多和最少的俯视图是关键.
14.9
【分析】过点D作DE⊥AB于E,则四边形BCDE是矩形,得BE=CD=2m,DE=BC=5m,再根据同一时刻,物高与影长成正比,可得,代入DE,即可求出AE长,即可由AB=AE+BE求解.
【详解】解:如图,过点D作DE⊥AB于E,
由题意,得AB⊥BC,DC⊥BC,
∵DE⊥AB,
∴四边形BCDE是矩形,
∴BE=CD=2m,DE=BC=5m,
由题意,得,
∴,
∴AE=7
∴AB=AE+BE=7+2=9(m),
答:这棵大树高为9m,
故答案为:9.
【点睛】本题考查解直角三角形的应用,熟练掌握同一时刻,物高与影长成正比是解题的关键.
15.24π
【分析】根据主视图确定圆柱的高为6,根据俯视图确定圆的直径为4即半径为2,利用公式计算即可.
【详解】∵
∴圆柱的高为6,圆的直径为4即半径为2,
∴圆柱的体积为==24π,
故答案为:24π.
【点睛】本题考查了圆柱的三视图,圆柱的体积,熟练读懂三视图,确定圆柱的高和直径是解题的关键.
16.7.5
【分析】根据木杆旋转时影子的长度变化确定木杆AB的长,然后利用相似三角形的性质求得EF的高度即可.
【详解】解:当旋转到达地面时,为最短影长,等于AB,
∵最小值3m,
∴AB=3m,
∵影长最大时,木杆与光线垂直,
即AC=5m,
∴BC=4 m,
又可得△CAB∽△CFE,
∴
∵AE=5m,
∴
解得:EF=7.5m
故答案为7.5.
【点睛】本题考查了中心投影和相似三角形的判定及性质的知识,解题的关键是根据影子的变化确定木杆的长度.
17.3
【详解】解:如图,∵CD∥AB∥MN,
∴△ABE∽△CDE,△ABF∽△MNF,
∴,
即,
解得:AB=3m,
故答案为:3
18. 10
【分析】过点O作AC、BD的平行线,交CD于H,过点O作水平线OJ交BD于点J,过点B作BI⊥OJ,垂足为I,延长MO,使得OK=OB,求出CH的长度,根据,求出OM的长度,证明,得出,,求出IJ、BI、OI的长度,用勾股定理求出OB的长,即可算出所求长度.
【详解】如图,过点O作AC、BD的平行线,交CD于H,过点O作水平线OJ交BD于点J,过点B作BI⊥OJ,垂足为I,延长MO,使得OK=OB,
由题意可知,点O是AB的中点,
∵,
∴点H是CD的中点,
∵,
∴,
∴,
又∵由题意可知:,
∴,解得,
∴点O、M之间的距离等于,
∵BI⊥OJ,
∴,
∵由题意可知:,
又∵,
∴,
∴,
∴,
∴,,
∵,
∴四边形OHDJ是平行四边形,
∴,
∵,
∴,,,
∵在中,由勾股定理得:,
∴,
∴,
∴,
∴叶片外端离地面的最大高度等于,
故答案为:10,.
【点睛】本题主要考查了投影和相似的应用,及勾股定理和平行四边形的判定与性质,正确作出辅助线是解答本题的关键.
19.(1)画图见解析;(2)DE=4
【分析】(1)连接CB延长CB交DE于O,点O即为所求.连接OG,延长OG交DF于H.线段FH即为所求.
(2)根据,可得 ,即可推出DO=4m.
【详解】(1)解:如图,点O为灯泡所在的位置,线段FH为小亮在灯光下形成的影子.
(2)解:由已知可得,,
∴,
∴OD=4m,
∴灯泡的高为4m.
【点睛】本题考查中心投影、解题的关键是正确画出图形,记住物长与影长的比的定值,属于基础题,中考常考题型.
20.(1)路灯A有6米高(2)王华的影子长米.
【详解】试题分析:22. 解:(1)由题可知AB//MC//NE,
∴,而MC=NE
∴
∵CD=1米,EF=2米,BF=BD+4,∴BD=4米,∴AB==6米
所以路灯A有6米高
(2) 依题意,设影长为x,则解得米
答:王华的影子长米.
考点:相似三角形性质
点评:本题难度较低,主要考查学生对相似三角形性质解决实际生活问题的能力.为中考常考题型,要求学生牢固掌握解题技巧.
21.0.7米
【分析】直接利用已知得出∠BAC=∠BCA,则BC=AB,再得出BF的长,求出x的值即可.
【详解】解:如图所示:延长AB,
∵CDAB,
∴∠CAB=30°,∠CBF=60°,
∴∠BCA=60°﹣30°=30°,即∠BAC=∠BCA,
∴BC=AB=3m,
在Rt△BCF中,BC=3m,∠CBF=60°,
∴BF=BC=1.5m,
故x=BF﹣EF=1.5﹣0.8=0.7(m),
答:这时汽车车头与斑马线的距离x是0.7m.
【点睛】考查了含30度角的直角三角形,正确得出BF的长是解题关键.
22.见解析
【分析】根据几何体的三视图的性质作图即可.
【详解】如图所示,即为所求.
【点睛】本题考查了几何体三视图的问题,掌握几何体三视图的性质是解题的关键.
23.(1)见解析
(2)24
【分析】(1)从正面看有2列,每列小正方形数目分别为2,3;从左面看有2列,每列小正方形数目分别为3,1;
(2)上面共有3个小正方形,下面共有3个小正方形;左面共有4个小正方形,右面共有4个正方形;前面共有5个小正方形,后面共有5个正方形,继而可得出表面积.
【详解】(1)解:从正面看有2列,每列小正方形数目分别为2,3;从左面看有2列,每列小正方形数目分别为3,1,
图形分别如下:
(2).
∴这个组合几何体的表面积为个平方单位.
【点睛】此题考查了简单几何体的三视图及几何体的表面积的计算,解答本题的关键是掌握三视图的观察方法,在计算表面积时容易出错,要一个面一个面的进行查找,避免遗漏.
24.(1)4,12,20
(2)第10个几何体中只有2个面涂色的小立方体的块数共有76个
(3)前100个几何体中只有2个面涂色的小立方体的个数的和为40000个
【分析】(1)第1个几何体中最底层的4个角的小立方体只有2个面涂色;第2个几何体中只有2个面涂色的小立方体共有3×4=12(个);第3个几何体中只有2个面涂色的小立方体共有5×4=20(个);
(2)根据所给图形中只有2个面涂色的小立方体的块数得到第n个几何体中只有2个面涂色的小立方体的块数与4的倍数的关系即可;
(3)根据(2)得到的规律,进行计算即可.
【详解】(1)解:观察图形可得第1个几何体中最底层的4个角的小立方体只有2个面涂色;
第2个几何体中只有2个面涂色的小立方体共有3×4=12(个);
第3个几何体中只有2个面涂色的小立方体共有5×4=20(个).
故答案为:4,12,20;
(2)解:观察图形可知:图①中,只有2个面涂色的小立方体共有4个;
图②中,只有2个面涂色的小立方体共有12个;
图③中,只有2个面涂色的小立方体共有20个.
4,12,20都是4的倍数,可分别写成4×1,4×3,4×5的形式,
因此,第n个图中两面涂色的小立方体的块数共有:4(2n﹣1)=8n﹣4,
则第10个几何体中只有2个面涂色的小立方体的块数共有8×10﹣4=76(个);
(3)解:(8×1﹣4)+(8×2﹣4)+(8×3﹣4)+(8×4﹣4)+(8×5﹣4)+…+(8×100﹣4)
=8(1+2+3+4+…+100)﹣100×4
=40000(个).
故前100个几何体中只有2个面涂色的小立方体的个数的和为40000个.
【点睛】本题考查了认识立体图形,图形的变化规律.得到所求块数与4的倍数的关系是解决本题的关键.
个数的和为40000个.
答案第1页,共2页
答案第1页,共2页
