专题27.29相似三角形几何模型-X型图 知识讲解(含解析)2023-2024学年九年级数学下册人教版专项讲练
文档属性
| 名称 | 专题27.29相似三角形几何模型-X型图 知识讲解(含解析)2023-2024学年九年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 437.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 18:51:02 | ||
图片预览



文档简介
专题27.29 相似三角形几何模型-X型图(知识讲解)
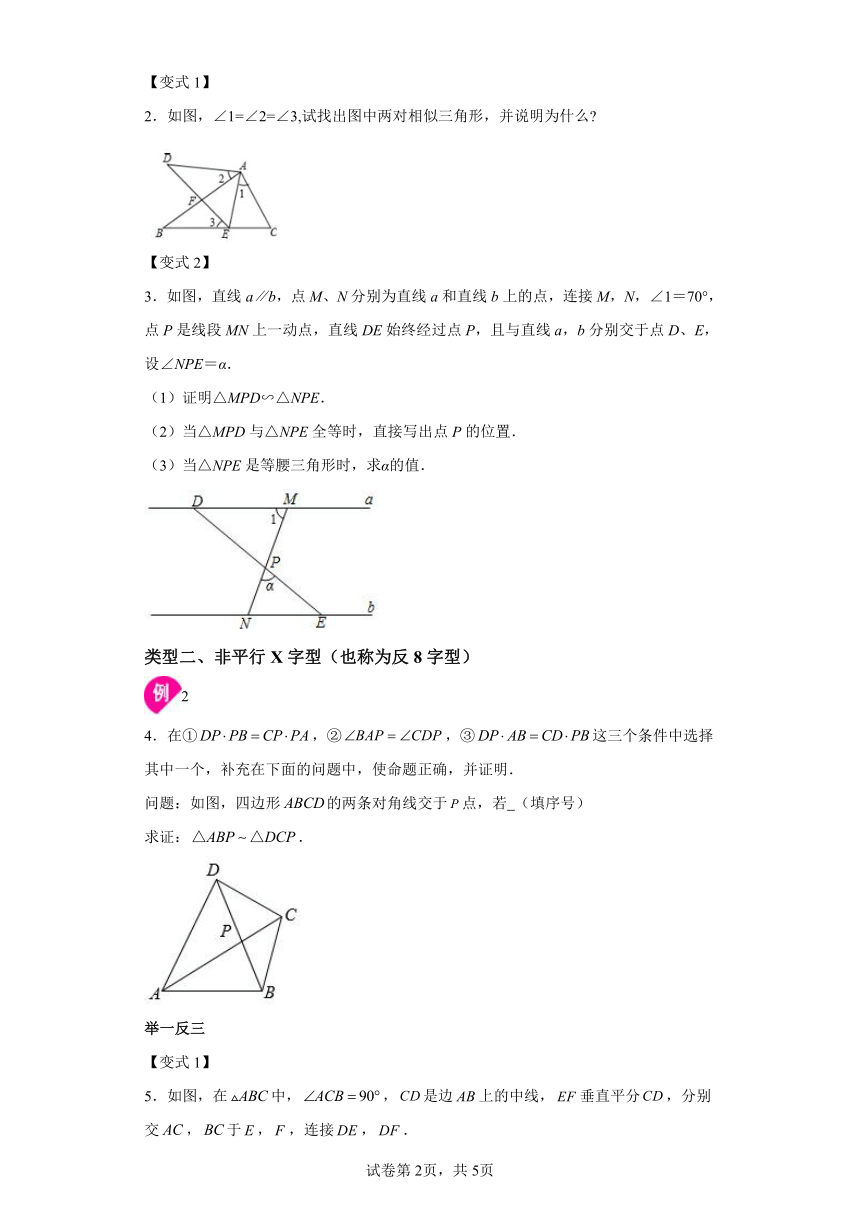
模型一:平行X字型
如图一:在DCAB,
模型二:非平行X字型(也称反X字型)
如图二:
模型三:双(多)X字型
如图三ADBC,AB、CD相交于点O,过点O的线段EF交AD、BC于E、F
图一 图二 图三
类型一、平行X字型(也称为8字型)
1
1.如图,在中,点,分别在边、上,与相交于点,且,,.求证:.
举一反三
【变式1】
2.如图,∠1=∠2=∠3,试找出图中两对相似三角形,并说明为什么
【变式2】
3.如图,直线a∥b,点M、N分别为直线a和直线b上的点,连接M,N,∠1=70°,点P是线段MN上一动点,直线DE始终经过点P,且与直线a,b分别交于点D、E,设∠NPE=α.
(1)证明△MPD∽△NPE.
(2)当△MPD与△NPE全等时,直接写出点P的位置.
(3)当△NPE是等腰三角形时,求α的值.
类型二、非平行X字型(也称为反8字型)
2
4.在①,②,③这三个条件中选择其中一个,补充在下面的问题中,使命题正确,并证明.
问题:如图,四边形的两条对角线交于点,若 (填序号)
求证:.
举一反三
【变式1】
5.如图,在中,,是边上的中线,垂直平分,分别交,于,,连接,.
(1)求证:.
(2)当,时,求线段的长.
【变式2】
6.如图,AC,BD相交于的点O,且∠ABO=∠C.求证:△AOB∽△DOC.
类型三、A、X字型综合
3
7.如图,在 ABCD中,AC,BD交于点O,点M是AD的中点,连接MC交BD于点N,ON=1.
(1)求证:△DMN∽△BCN;
(2)求BD的长;
(3)若△DCN的面积为2,直接写出四边形ABNM的面积.
举一反三
【变式1】
8.如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,延长FE与直线CD相交于点G,连接FC(AB>AE).
(1)求证:△AEF∽△DCE;
(2)△AEF与△ECF是否相似?若相似,证明你的结论;若不相似,请说明理由;
(3)设,是否存在这样的k值,使得△AEF与△BFC相似?若存在,证明你的结论并求出k的值;若不存在,请说明理由.
【变式2】
9.如图,四边形ABCD为正方形,且E是边BC延长线上一点,过点B作BF⊥DE于F点,交AC于H点,交CD于G点.
(1)求证:△BGC∽△DGF;
(2)求证:;
(3)若点G是DC中点,求的值.
【变式3】
10.已知:如图,两个和中,,且点在一条直线上,联结与交于点F.
(1)求证:;
(2)如果,求证:.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.答案见解析
【分析】利用比例线段来证明相似三角形即可.
【详解】解:,,
,
,,
,
,
.
【点睛】本题主要考查三角形相似的判定,掌握三角形相似的判定定理是解题的关键.
2.△AFD∽△EFB,△ABC∽△ADE;理由见解析.
【分析】根据两个三角形的两组角对应相等,那么这两个三角形互为相似三角形证明即可.
【详解】解:△AFD∽△EFB,△ABC∽△ADE.
理由如下:∵∠2=∠3,∠AFD=∠EFB
∴△AFD∽△EFB,
∴∠B=∠D.
∵∠1=∠2,
∴ ,
∴∠BAC=∠DAE,
∴△ABC∽△ADE.
【点睛】本题考查相似三角形的判定定理,熟记判定定理,本题用到了两组角对应相等的两个三角形互为相似三角形.
3.(1)见解析;(2)点P是MN的中点;(3)40° 或70° 或55°
【分析】(1)利用相似三角形的判定定理证明即可;
(2)根据全等三角形对应边相等得到MP=NP,即点P是MN的中点;
(3)需要分类讨论:PN=PE、PE=NE、PN=NE,再根据三角形内角和计算即可.
【详解】(1)证明:∵a∥b,
∴△MPD∽△NPE.
(2)∵a∥b,
∴∠MDP=∠NEP,
∴当△MPD与△NPE全等时, MP=NP,即点P是MN的中点;
(3)∵a∥b,
∴∠1=∠PNE=70°,
①若PN=PE时,
∴∠PNE=∠PEN=70°.
∴a=180°﹣∠PNE﹣∠PEN=180°﹣70°﹣70°=40°.
∴∠a=40°;
②若EP=EN时,则a=∠PNE=70°;
③若NP=NE 时,则∠PEN=α,此时2α=180°﹣∠PNE=110°,
∴α=∠PEN═55°;
综上所述,α的值是40° 或70° 或55°.
【点睛】本题考查了相似三角形的判定、全等三角形的性质、等腰三角形的性质,解题关键是熟知相关性质,会根据等腰三角形底边不同进行分类讨论.
4.①,证明见解析或②,证明见解析.
【分析】若选择条件①,可利用两边成比例且夹角相等的两个三角形相似;
若选择条件②,可利用两角相等的两个三角形相似.
【详解】解:选择条件①的证明为:
∵,
∴,
又∵,
∴;
选择条件②的证明为:
∵,
∴.
【点睛】本题考查相似三角形的判定定理,能熟记相似三角形的判定定理,并正确识图是解题关键.
5.(1)见解析
(2)
【分析】(1)如图(见解析),先根据线段垂直平分线的性质可得,,,再根据三角形全等的判定定理证出,根据全等三角形的性质可得,从而可得,然后根据相似三角形的判定即可得证;
(2)如图(见解析),延长至,使,连接,,先根据线段垂直平分线的判定与性质可得,再根据三角形全等的判定定理证出,根据全等三角形的性质可得,,然后根据平行线的判定与性质可得,最后在中,利用勾股定理即可得.
【详解】(1)证明:∵垂直平分,
∴,,,
在和中,,
∴,
∴,
∵,,
∴,
∴,
在和中,,
∴.
(2)解:如图,延长至,使,连接,.
则垂直平分,
,
是边上的中线,
∴,
在和中,,
∴,
∴,,
∴,
∴,
∴,
∴.
【点睛】本题考查了相似三角形的判定、三角形全等的判定定理与性质、线段垂直平分线的判定与性质等知识点,较难的是题(2),构造全等三角形和直角三角形是解题关键.
6.见解析
【分析】利用对顶角相等得到∠AOB=∠COD,再结合已知条件及相似三角形的判定定理即可求解.
【详解】证明:∵AC,BD相交于的点O,
∴∠AOB=∠DOC,
又∵∠ABO=∠C,
∴△AOB∽△DOC.
【点睛】本题考查了相似三角形的判定定理:若一对三角形的两组对应角相等,则这两个三角形相似,由此即可求解.
7.(1)见解析
(2)6
(3)5
【分析】(1)根据平行四边形的性质可得ADBC,从而证明8字模型相似三角形△DMN∽△BCN;
(2)由△DMN∽△BCN,可得到DN:BN=1:2,设OB=OD=x,表示出BN与DN,求出x的值,即可确定出BD的长;
(3)根据△MND∽△CNB且相似比为1:2,得到CN=2MN,BN=2DN.已知△DCN的面积,则由线段之比,得到△MND与△CNB的面积,从而得到S△ABD=S△BCD=S△BCN+S△CND,最后由S四边形ABNM=S△ABD-S△MND求解.
【详解】(1)证明:∵四边形ABCD是平行四边形,
∴ADBC,
∴∠DMN=∠BCN,∠MDN=∠NBC,
∴△DMN∽△BCN;
(2)解:∵四边形ABCD是平行四边形,
∴AD=BC,OB=OD=BD,
∵△DMN∽△BCN,
∴,
∵M为AD中点,
∴AD=2DM,
∴BC=2DM,
∴BN=2DN,
设OB=OD=x,
∴BD=2x,
∴BN=OB+ON=x+1,DN=OD-ON=x-1,
∴x+1=2(x-1),
解得:x=3,
∴BD=2x=6,
∴BD的长为6;
(3)解:∵△MND∽△CNB,
∴DM:BC=MN:CN=DN:BN=1:2,
∵△DCN的面积为2,
∴S△MND=S△CND=1,S△BNC=2S△CND=4,
∴S△ABD=S△BCD=S△BCN+S△CND=4+2=6,
∴S四边形ABNM=S△ABD-S△MND=6-1=5,
∴四边形ABNM的面积为5.
【点睛】本题考查了相似三角形的判定与性质,平行四边形的性质,熟练掌握相似三角形的面积比等于相似比的平方,等高三角形面积的比等于其对应底的比是解题的关键.
8.(1)见解析
(2)相似,证明见解析
(3)存在,
【分析】(1)由题意可得∠AEF+∠DEC=90°,又由∠AEF+∠AFE=90°,可得∠DEC=∠AFE,据此证得结论;
(2)根据题意可证得Rt△AEF≌Rt△DEG(ASA),可得EF=EG,∠AFE=∠EGC,可得CE垂直平分FG,△CGF是等腰三角形,据此即可证得△AEF与△ECF相似;
(3)假设△AEF与△BFC相似,存在两种情况:①当∠AFE=∠BCF,可得∠EFC=90°,根据题意可知此种情况不成立;②当∠AFE=∠BFC,使得△AEF与△BFC相似,设BC=a,则AB=ka,可得AF=,BF=,再由△AEF∽△DCE,即可求得k值.
【详解】(1)证明:∵EF⊥EC,
∴∠FEC=90°,
∴∠AEF+∠DEC=90°,
∵∠AEF+∠AFE=90°,
∴∠DEC=∠AFE,
又∵∠A=∠EDC=90°,
∴△AEF∽△DCE;
(2)解:△AEF∽△ECF.
理由:∵E为AD的中点,
∴AE=DE,
∵∠AEF=∠DEG,∠A=∠EDG,
∴△AEF≌△DEG(ASA),
∴EF=EG,∠AFE=∠EGC.
又∵EF⊥CE,
∴CE垂直平分FG,
∴△CGF是等腰三角形.
∴∠AFE=∠EGC=∠EFC.
又∵∠A=∠FEC=90°,
∴△AEF∽△ECF;
(3)解:存在使得△AEF与△BFC相似.
理由:
假设△AEF与△BFC相似,存在两种情况:
①当∠AFE=∠BCF,则有∠AFE与∠BFC互余,于是∠EFC=90°,因此此种情况不成立;
②当∠AFE=∠BFC,使得△AEF与△BFC相似,
设BC=a,则AB=ka,
∵△AEF∽△BCF,
∴,
∴AF=,BF=,
∵△AEF∽△DCE,
∴,即,
解得,.
∴存在使得△AEF与△BFC相似.
【点睛】本题考查了矩形的性质,相似三角形的判定及性质,全等三角形的判定与及性质,等腰三角形的判定及性质,采用分类讨论的思想是解决本题的关键.
9.(1)见解析
(2)见解析
(3)
【分析】(1)由正方形性质和题干已知垂直条件得直角相等,后由对顶角相等,进而得到△BGC∽△DCF.
(2)由第一问的结论可得到相似比,既有,然后因为正方形四边相等,进行等量代换即可求出证明出结论.
(3)通过ASA判定出△BGC≌△DEC,进而根据第一问结论可得△BGC∽△DGF,然后通过相似比设未知数,赋值,即可求出的值.
【详解】(1)证明:∵四边形ABCD是正方形
∴
∵
∴
∴,
又∵,
∴△BGC∽△DCF.
(2)证明:由(1)知△BGC∽△DGF,
∴,
∴
∵四边形ABCD是正方形,
∴
∴.
(3)解:由(1)知△BCC∽△DGF,
∴,
在△BGC与△DEC中,
∴△BGC≌△DEC(ASA)
∴
∵G是CD中点
∴
∴
∵△BGC∽△DGF
∴
在Rt△BGC中,设,则,
∴
∴
【点睛】本题主要考查了正方形的性质,全等三角形判定和性质,相似三角形判定和性质等知识点,熟练运用相似三角形判定和性质是解题的关键.
10.(1)证明见解析
(2)证明见解析
【分析】(1)根据已知易证,然后利用相似三角形的性质可得,,从而可得,进而证明8字模型相似三角形,最后利用相似三角形的性质可得,即可解答;
(2)根据已知易证,从而利用相似三角形的性质可得,进而可得,然后利用(1)的结论可证,再利用全等三角形的性质即可解答.
【详解】(1)证明:∵,
∴,
∵,
∴,
∴,,
∴,
∴,
∴,
∴,
∴;
(2)
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
【点睛】本题考查了全等三角形的判定与性质,相似三角形的判定与性质,熟练掌握全等三角形的判定与性质,以及相似三角形的判定与性质是解题的关键.
答案第1页,共2页
答案第1页,共2页
模型一:平行X字型
如图一:在DCAB,
模型二:非平行X字型(也称反X字型)
如图二:
模型三:双(多)X字型
如图三ADBC,AB、CD相交于点O,过点O的线段EF交AD、BC于E、F
图一 图二 图三
类型一、平行X字型(也称为8字型)
1
1.如图,在中,点,分别在边、上,与相交于点,且,,.求证:.
举一反三
【变式1】
2.如图,∠1=∠2=∠3,试找出图中两对相似三角形,并说明为什么
【变式2】
3.如图,直线a∥b,点M、N分别为直线a和直线b上的点,连接M,N,∠1=70°,点P是线段MN上一动点,直线DE始终经过点P,且与直线a,b分别交于点D、E,设∠NPE=α.
(1)证明△MPD∽△NPE.
(2)当△MPD与△NPE全等时,直接写出点P的位置.
(3)当△NPE是等腰三角形时,求α的值.
类型二、非平行X字型(也称为反8字型)
2
4.在①,②,③这三个条件中选择其中一个,补充在下面的问题中,使命题正确,并证明.
问题:如图,四边形的两条对角线交于点,若 (填序号)
求证:.
举一反三
【变式1】
5.如图,在中,,是边上的中线,垂直平分,分别交,于,,连接,.
(1)求证:.
(2)当,时,求线段的长.
【变式2】
6.如图,AC,BD相交于的点O,且∠ABO=∠C.求证:△AOB∽△DOC.
类型三、A、X字型综合
3
7.如图,在 ABCD中,AC,BD交于点O,点M是AD的中点,连接MC交BD于点N,ON=1.
(1)求证:△DMN∽△BCN;
(2)求BD的长;
(3)若△DCN的面积为2,直接写出四边形ABNM的面积.
举一反三
【变式1】
8.如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,延长FE与直线CD相交于点G,连接FC(AB>AE).
(1)求证:△AEF∽△DCE;
(2)△AEF与△ECF是否相似?若相似,证明你的结论;若不相似,请说明理由;
(3)设,是否存在这样的k值,使得△AEF与△BFC相似?若存在,证明你的结论并求出k的值;若不存在,请说明理由.
【变式2】
9.如图,四边形ABCD为正方形,且E是边BC延长线上一点,过点B作BF⊥DE于F点,交AC于H点,交CD于G点.
(1)求证:△BGC∽△DGF;
(2)求证:;
(3)若点G是DC中点,求的值.
【变式3】
10.已知:如图,两个和中,,且点在一条直线上,联结与交于点F.
(1)求证:;
(2)如果,求证:.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.答案见解析
【分析】利用比例线段来证明相似三角形即可.
【详解】解:,,
,
,,
,
,
.
【点睛】本题主要考查三角形相似的判定,掌握三角形相似的判定定理是解题的关键.
2.△AFD∽△EFB,△ABC∽△ADE;理由见解析.
【分析】根据两个三角形的两组角对应相等,那么这两个三角形互为相似三角形证明即可.
【详解】解:△AFD∽△EFB,△ABC∽△ADE.
理由如下:∵∠2=∠3,∠AFD=∠EFB
∴△AFD∽△EFB,
∴∠B=∠D.
∵∠1=∠2,
∴ ,
∴∠BAC=∠DAE,
∴△ABC∽△ADE.
【点睛】本题考查相似三角形的判定定理,熟记判定定理,本题用到了两组角对应相等的两个三角形互为相似三角形.
3.(1)见解析;(2)点P是MN的中点;(3)40° 或70° 或55°
【分析】(1)利用相似三角形的判定定理证明即可;
(2)根据全等三角形对应边相等得到MP=NP,即点P是MN的中点;
(3)需要分类讨论:PN=PE、PE=NE、PN=NE,再根据三角形内角和计算即可.
【详解】(1)证明:∵a∥b,
∴△MPD∽△NPE.
(2)∵a∥b,
∴∠MDP=∠NEP,
∴当△MPD与△NPE全等时, MP=NP,即点P是MN的中点;
(3)∵a∥b,
∴∠1=∠PNE=70°,
①若PN=PE时,
∴∠PNE=∠PEN=70°.
∴a=180°﹣∠PNE﹣∠PEN=180°﹣70°﹣70°=40°.
∴∠a=40°;
②若EP=EN时,则a=∠PNE=70°;
③若NP=NE 时,则∠PEN=α,此时2α=180°﹣∠PNE=110°,
∴α=∠PEN═55°;
综上所述,α的值是40° 或70° 或55°.
【点睛】本题考查了相似三角形的判定、全等三角形的性质、等腰三角形的性质,解题关键是熟知相关性质,会根据等腰三角形底边不同进行分类讨论.
4.①,证明见解析或②,证明见解析.
【分析】若选择条件①,可利用两边成比例且夹角相等的两个三角形相似;
若选择条件②,可利用两角相等的两个三角形相似.
【详解】解:选择条件①的证明为:
∵,
∴,
又∵,
∴;
选择条件②的证明为:
∵,
∴.
【点睛】本题考查相似三角形的判定定理,能熟记相似三角形的判定定理,并正确识图是解题关键.
5.(1)见解析
(2)
【分析】(1)如图(见解析),先根据线段垂直平分线的性质可得,,,再根据三角形全等的判定定理证出,根据全等三角形的性质可得,从而可得,然后根据相似三角形的判定即可得证;
(2)如图(见解析),延长至,使,连接,,先根据线段垂直平分线的判定与性质可得,再根据三角形全等的判定定理证出,根据全等三角形的性质可得,,然后根据平行线的判定与性质可得,最后在中,利用勾股定理即可得.
【详解】(1)证明:∵垂直平分,
∴,,,
在和中,,
∴,
∴,
∵,,
∴,
∴,
在和中,,
∴.
(2)解:如图,延长至,使,连接,.
则垂直平分,
,
是边上的中线,
∴,
在和中,,
∴,
∴,,
∴,
∴,
∴,
∴.
【点睛】本题考查了相似三角形的判定、三角形全等的判定定理与性质、线段垂直平分线的判定与性质等知识点,较难的是题(2),构造全等三角形和直角三角形是解题关键.
6.见解析
【分析】利用对顶角相等得到∠AOB=∠COD,再结合已知条件及相似三角形的判定定理即可求解.
【详解】证明:∵AC,BD相交于的点O,
∴∠AOB=∠DOC,
又∵∠ABO=∠C,
∴△AOB∽△DOC.
【点睛】本题考查了相似三角形的判定定理:若一对三角形的两组对应角相等,则这两个三角形相似,由此即可求解.
7.(1)见解析
(2)6
(3)5
【分析】(1)根据平行四边形的性质可得ADBC,从而证明8字模型相似三角形△DMN∽△BCN;
(2)由△DMN∽△BCN,可得到DN:BN=1:2,设OB=OD=x,表示出BN与DN,求出x的值,即可确定出BD的长;
(3)根据△MND∽△CNB且相似比为1:2,得到CN=2MN,BN=2DN.已知△DCN的面积,则由线段之比,得到△MND与△CNB的面积,从而得到S△ABD=S△BCD=S△BCN+S△CND,最后由S四边形ABNM=S△ABD-S△MND求解.
【详解】(1)证明:∵四边形ABCD是平行四边形,
∴ADBC,
∴∠DMN=∠BCN,∠MDN=∠NBC,
∴△DMN∽△BCN;
(2)解:∵四边形ABCD是平行四边形,
∴AD=BC,OB=OD=BD,
∵△DMN∽△BCN,
∴,
∵M为AD中点,
∴AD=2DM,
∴BC=2DM,
∴BN=2DN,
设OB=OD=x,
∴BD=2x,
∴BN=OB+ON=x+1,DN=OD-ON=x-1,
∴x+1=2(x-1),
解得:x=3,
∴BD=2x=6,
∴BD的长为6;
(3)解:∵△MND∽△CNB,
∴DM:BC=MN:CN=DN:BN=1:2,
∵△DCN的面积为2,
∴S△MND=S△CND=1,S△BNC=2S△CND=4,
∴S△ABD=S△BCD=S△BCN+S△CND=4+2=6,
∴S四边形ABNM=S△ABD-S△MND=6-1=5,
∴四边形ABNM的面积为5.
【点睛】本题考查了相似三角形的判定与性质,平行四边形的性质,熟练掌握相似三角形的面积比等于相似比的平方,等高三角形面积的比等于其对应底的比是解题的关键.
8.(1)见解析
(2)相似,证明见解析
(3)存在,
【分析】(1)由题意可得∠AEF+∠DEC=90°,又由∠AEF+∠AFE=90°,可得∠DEC=∠AFE,据此证得结论;
(2)根据题意可证得Rt△AEF≌Rt△DEG(ASA),可得EF=EG,∠AFE=∠EGC,可得CE垂直平分FG,△CGF是等腰三角形,据此即可证得△AEF与△ECF相似;
(3)假设△AEF与△BFC相似,存在两种情况:①当∠AFE=∠BCF,可得∠EFC=90°,根据题意可知此种情况不成立;②当∠AFE=∠BFC,使得△AEF与△BFC相似,设BC=a,则AB=ka,可得AF=,BF=,再由△AEF∽△DCE,即可求得k值.
【详解】(1)证明:∵EF⊥EC,
∴∠FEC=90°,
∴∠AEF+∠DEC=90°,
∵∠AEF+∠AFE=90°,
∴∠DEC=∠AFE,
又∵∠A=∠EDC=90°,
∴△AEF∽△DCE;
(2)解:△AEF∽△ECF.
理由:∵E为AD的中点,
∴AE=DE,
∵∠AEF=∠DEG,∠A=∠EDG,
∴△AEF≌△DEG(ASA),
∴EF=EG,∠AFE=∠EGC.
又∵EF⊥CE,
∴CE垂直平分FG,
∴△CGF是等腰三角形.
∴∠AFE=∠EGC=∠EFC.
又∵∠A=∠FEC=90°,
∴△AEF∽△ECF;
(3)解:存在使得△AEF与△BFC相似.
理由:
假设△AEF与△BFC相似,存在两种情况:
①当∠AFE=∠BCF,则有∠AFE与∠BFC互余,于是∠EFC=90°,因此此种情况不成立;
②当∠AFE=∠BFC,使得△AEF与△BFC相似,
设BC=a,则AB=ka,
∵△AEF∽△BCF,
∴,
∴AF=,BF=,
∵△AEF∽△DCE,
∴,即,
解得,.
∴存在使得△AEF与△BFC相似.
【点睛】本题考查了矩形的性质,相似三角形的判定及性质,全等三角形的判定与及性质,等腰三角形的判定及性质,采用分类讨论的思想是解决本题的关键.
9.(1)见解析
(2)见解析
(3)
【分析】(1)由正方形性质和题干已知垂直条件得直角相等,后由对顶角相等,进而得到△BGC∽△DCF.
(2)由第一问的结论可得到相似比,既有,然后因为正方形四边相等,进行等量代换即可求出证明出结论.
(3)通过ASA判定出△BGC≌△DEC,进而根据第一问结论可得△BGC∽△DGF,然后通过相似比设未知数,赋值,即可求出的值.
【详解】(1)证明:∵四边形ABCD是正方形
∴
∵
∴
∴,
又∵,
∴△BGC∽△DCF.
(2)证明:由(1)知△BGC∽△DGF,
∴,
∴
∵四边形ABCD是正方形,
∴
∴.
(3)解:由(1)知△BCC∽△DGF,
∴,
在△BGC与△DEC中,
∴△BGC≌△DEC(ASA)
∴
∵G是CD中点
∴
∴
∵△BGC∽△DGF
∴
在Rt△BGC中,设,则,
∴
∴
【点睛】本题主要考查了正方形的性质,全等三角形判定和性质,相似三角形判定和性质等知识点,熟练运用相似三角形判定和性质是解题的关键.
10.(1)证明见解析
(2)证明见解析
【分析】(1)根据已知易证,然后利用相似三角形的性质可得,,从而可得,进而证明8字模型相似三角形,最后利用相似三角形的性质可得,即可解答;
(2)根据已知易证,从而利用相似三角形的性质可得,进而可得,然后利用(1)的结论可证,再利用全等三角形的性质即可解答.
【详解】(1)证明:∵,
∴,
∵,
∴,
∴,,
∴,
∴,
∴,
∴,
∴;
(2)
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
【点睛】本题考查了全等三角形的判定与性质,相似三角形的判定与性质,熟练掌握全等三角形的判定与性质,以及相似三角形的判定与性质是解题的关键.
答案第1页,共2页
答案第1页,共2页
