专题27.36相似三角形几何模型-双垂线等角 知识讲解(含解析)2023-2024学年九年级数学下册人教版专项讲练
文档属性
| 名称 | 专题27.36相似三角形几何模型-双垂线等角 知识讲解(含解析)2023-2024学年九年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 597.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 18:52:31 | ||
图片预览


文档简介
专题27.36 相似三角形几何模型-双垂线等角
(知识讲解)
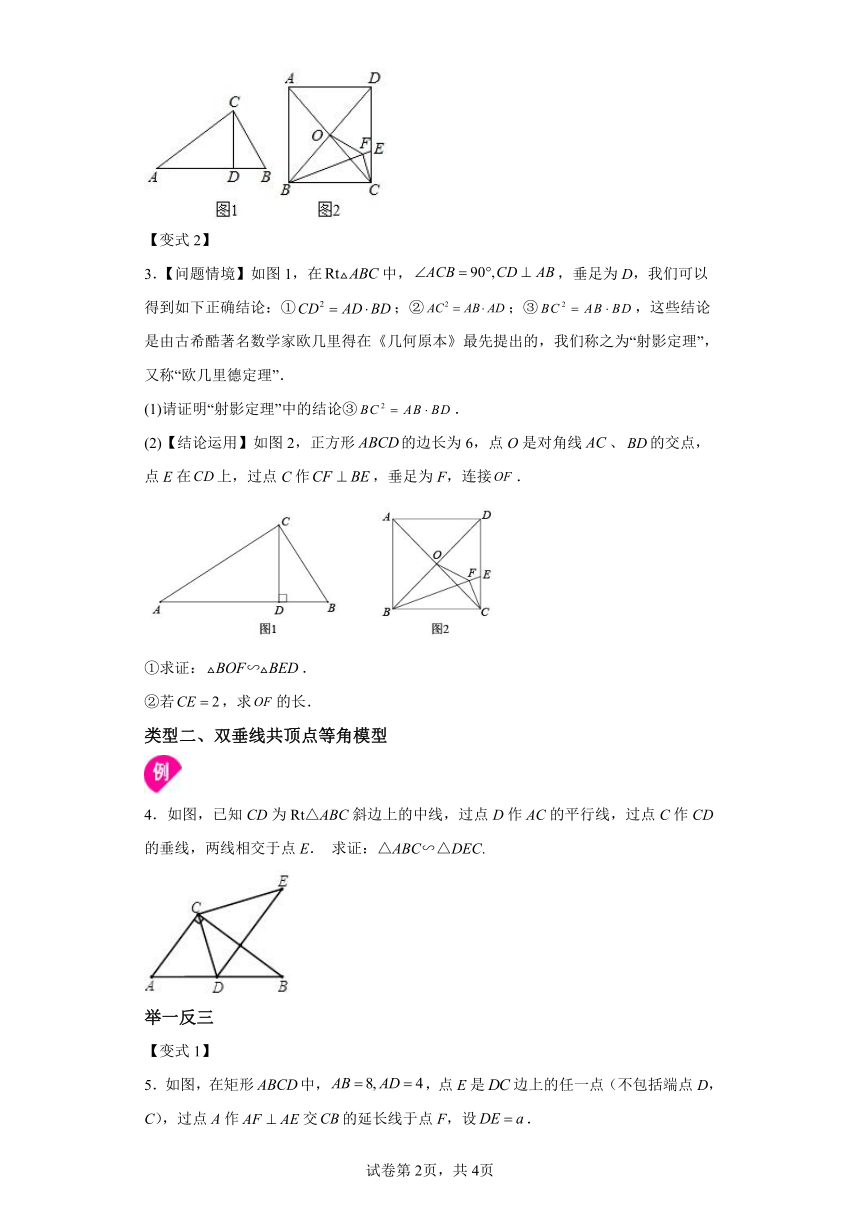
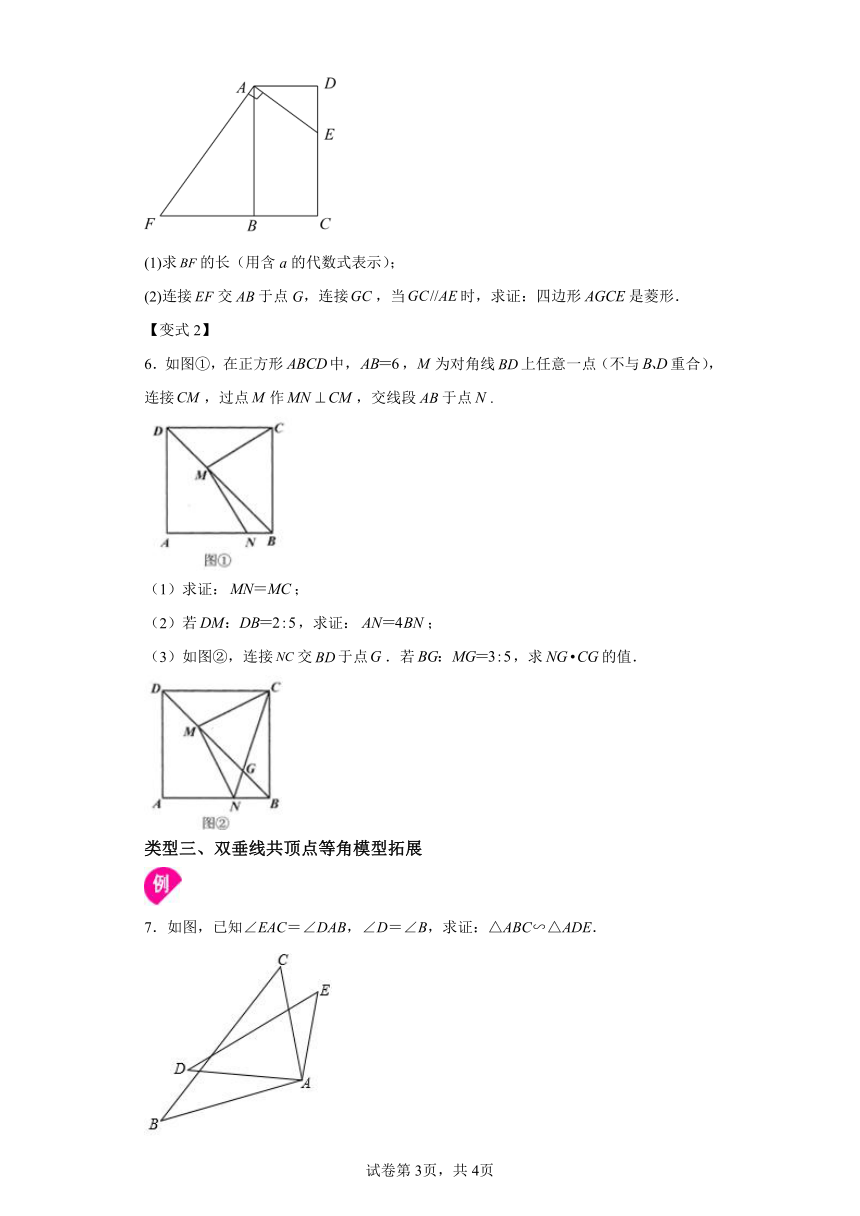
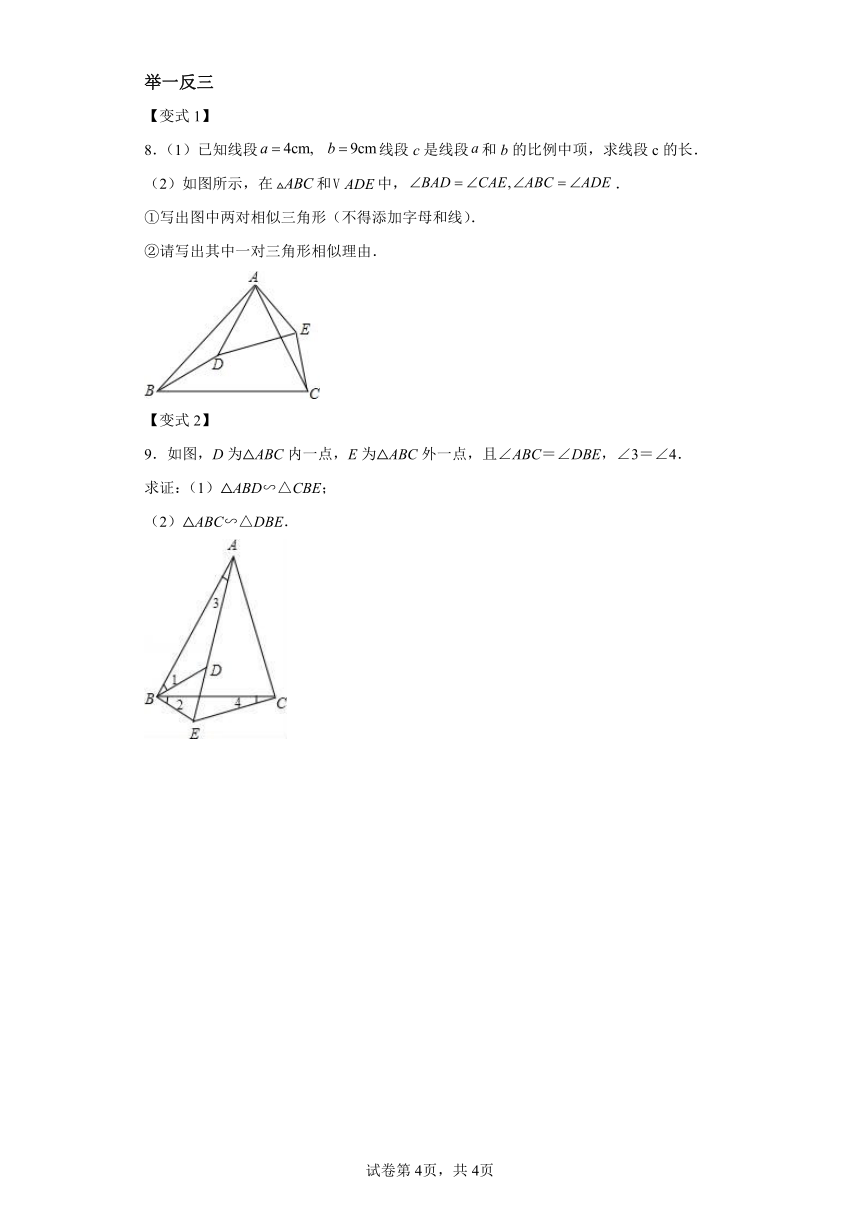
【非共顶点双垂线等角模型】
【双垂线共顶点等角模型】
【双垂线共顶点等角模型拓展】
【典型例题】
类型一、非共顶点双垂线等角模型
1.如图,在中,CD是斜边AB上的高.
求证:.
举一反三
【变式1】
2.(1)问题情境:如图1,Rt中,∠ACB=90°,CD⊥AB,我们可以利用与相似证明AC2=AD AB,这个结论我们称之为射影定理,试证明这个定理.
(2)结论运用:如图2,正方形ABCD的边长为6,点O是对角线AC,BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,试利用射影定理证明.
【变式2】
3.【问题情境】如图1,在中,,垂足为D,我们可以得到如下正确结论:①;②;③,这些结论是由古希酷著名数学家欧几里得在《几何原本》最先提出的,我们称之为“射影定理”,又称“欧几里德定理”.
(1)请证明“射影定理”中的结论③.
(2)【结论运用】如图2,正方形的边长为6,点O是对角线、的交点,点E在上,过点C作,垂足为F,连接.
①求证:.
②若,求的长.
类型二、双垂线共顶点等角模型
4.如图,已知CD为Rt△ABC斜边上的中线,过点D作AC的平行线,过点C作CD的垂线,两线相交于点E. 求证:△ABC∽△DEC.
举一反三
【变式1】
5.如图,在矩形中,,点E是边上的任一点(不包括端点D,C),过点A作交的延长线于点F,设.
(1)求的长(用含a的代数式表示);
(2)连接交于点G,连接,当时,求证:四边形是菱形.
【变式2】
6.如图①,在正方形中,,为对角线上任意一点(不与重合),连接,过点作,交线段于点.
(1)求证:;
(2)若,求证:;
(3)如图②,连接交于点.若,求的值.
类型三、双垂线共顶点等角模型拓展
7.如图,已知∠EAC=∠DAB,∠D=∠B,求证:△ABC∽△ADE.
举一反三
【变式1】
8.(1)已知线段线段c是线段和b的比例中项,求线段c的长.
(2)如图所示,在和中,.
①写出图中两对相似三角形(不得添加字母和线).
②请写出其中一对三角形相似理由.
【变式2】
9.如图,D为△ABC内一点,E为△ABC外一点,且∠ABC=∠DBE,∠3=∠4.
求证:(1)△ABD∽△CBE;
(2)△ABC∽△DBE.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.见解析
【分析】根据两个角相等的两个三角形相似进行证明即可.
【详解】证明:如图,
∵在中,CD是斜边AB上的高
∴
∵是公共角
∴.
【点睛】本题考查了相似三角形的判定,解题关键是熟练掌握相似三角形的判定定理,准确运用进行推理证明.
2.(1)见解析;(2)见解析.
【分析】(1)由AA证明,再结合相似三角形对应边成比例即可解题;
(2)根据正方形的性质及射影定理解得BC2=BO BD,BC2=BF BE,再运用SAS证明△BOF∽△BED即可.
【详解】证明:(1)如图1,
(2)如图2,
∵四边形ABCD为正方形,
∴OC⊥BO,∠BCD=90°,
∴BC2=BO BD,
∵CF⊥BE,
∴BC2=BF BE,
∴BO BD=BF BE,即,
而∠OBF=∠EBD,
∴△BOF∽△BED.
【点睛】本题考查射影定理、相似三角形的判定与性质、正方形的性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.
3.(1)见解析;
(2)①见解析;②.
【分析】(1)由AA证明,再由相似三角形对应边称比例得到,继而解题;
(2)①由“射影定理”分别解得,,整理出,再结合即可证明;
②由勾股定理解得,再根据得到,代入数值解题即可.
【详解】(1)证明:
(2)①四边形ABCD是正方形
②在中,
在,
.
【点睛】本题考查相似三角形的综合题,涉及勾股定理、正方形等知识,是重要考点,掌握相关知识是解题关键.
4.见解析
【分析】根据直角三角形斜边上的中线等于斜边的一半可得出CD=AD,进而可得出∠A=∠ACD,由平行线的性质可得出∠CDE=∠ACD=∠A,再结合∠ACB=∠DCE=90°,即可证出△ABC∽△DEC.
【详解】∵CD为Rt△ABC斜边上的中线,
∴.
∴.
∵DE∥AC.
∴.
∴.
∵,CE⊥CD,
∴ .
∴△ABC∽△DEC.
【点睛】本题考查相似三角形的判定与性质,直角三角形斜边上的中线,解题关键是找出证明三角形相似的条件.
5.(1)
(2)见详解
【分析】(1)根据矩形的性质可得,然后可证,进而根据相似三角形的性质可求解;
(2)如图,连接AC,由题意易证四边形是平行四边形,然后可得,进而可证,则可证,最后问题可求证.
【详解】(1)解:∵四边形是矩形,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵,,
∴;
(2)证明:由题意可得如图所示:
连接AC,
在矩形中,,,
∴,
∵,
∴四边形是平行四边形,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴四边形是菱形.
【点睛】本题主要考查相似三角形的性质与判定、矩形的性质及菱形的判定,熟练掌握相似三角形的性质与判定、矩形的性质及菱形的判定是解题的关键.
6.(1)见解析;(2)见解析;(3).
【分析】(1)如图,过分别作交于点,交于点,则四边形是平行四边形,先证明四边形是正方形,继而证明,即可得结论;
(2)由(1)得,,根据比例线段可得,,再根据可得,从而求得AN、BN长即可得结论;
(3)把绕点逆时针旋转得到,连接,,进而可推导得出,,证明是等腰直角三角形,继而证明,可得MG=HG,根据题意设,则,根据勾股定理可求得,再结合正方形的性质可求得a的值,继而证明, 根据相似三角形的性质即可求得答案.
【详解】(1)如图,过分别作交于点,交于点,则四边形是平行四边形,
四边形是正方形,
,,
,
平行四边形是正方形,
,
,
,
,
,
,
;
(2)由(1)得:,,
,
,,
,
,
,,
;
(3)把绕点逆时针旋转得到,连接,
,,
,,,.
,,
,,
是等腰直角三角形,
,
,
,
,
,
设,则,
在中,,则,
正方形的边长为,
,
,
,
,,
,,
,
,
.
【点睛】本题考查的是四边形的综合题,涉及了正方形判定与性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理等知识,综合性较强,正确把握相关的判定定理与性质定理是解题的关键.
7.见解析
【分析】由∠EAC=∠DAB,可推出∠BAC=∠DAE,再由∠B=∠D,即可证明△ABC∽△ADE.
【详解】解:∵∠EAC=∠DAB,
∴∠EAC+∠DAC=∠DAB+∠DAC,即∠BAC=∠DAE,
又∵∠B=∠D,
∴△ABC∽△ADE.
【点睛】本题主要考查了相似三角形的判定,熟知相似三角形的判定条件是解题的关键.
8.(1)6cm;(2)①△ABC∽△ADE,△ABD∽△ACE;②见解析
【分析】(1)根据线段比例中项的概念得出a:c=c:b,再根据a=4cm,b=9cm,求出c的值,注意把负值舍去.
(2)①根据有两组对角对应相等的三角形相似可得出△ABC∽△ADE,再由两组对应边的比相等且夹角对应相等的两个三角形相似可得出△ABD∽△ACE;
②由①中可得对应线段成比例,又根据其对应角相等,即可判定其相似.
【详解】解:(1)∵线段c是线段a和b的比例中项,a=4cm,b=9cm,
∴c2=ab=36,
解得:c=±6,
又∵线段是正数,
∴c=6cm.
(2)①由题意可得:△ABC∽△ADE,△ABD∽△ACE;
②证明:∵,
∴∠BAD+∠CAD=∠CAE+∠CAD,即∠BAC=∠DAE,
又∵,
∴△ABC∽△ADE,
∴,
∴AB×AE=AC×AD,
∴,
∵∠BAD=∠CAE,
∴△ABD∽△ACE.
【点睛】本题考查的是相似三角形的判定,熟记相似三角形的判定定理是解答此题的关键.
9.(1)证明见解析;(2)证明见解析;
【分析】(1)根据有两组角对应相等的两个三角形相似可判断△ABD∽△CBE;
(2)先利用得到∠1=∠2得到∠ABC=∠DBE,再利用△ABD∽△CBE得 , 根据比例的性质得到 , 然后根据两组对应边的比相等且夹角对应相等的两个三角形相似可判断△ABC与△DBE相似.
【详解】(1)相似.理由如下:
∵∠1=∠2,∠3=∠4.
∴△ABD∽△CBE;
(2)相似.理由如下:
∵∠1=∠2,
∴∠1+∠DBC=∠2+DBC,即∠ABC=∠DBE,
∵△ABD∽△CBE,
∴=,
∴=,
∴△ABC∽△DBE.
【点睛】本题考查了三角形相似的判定,熟练掌握三角形相似的判定方法是解题关键.
答案第1页,共2页
答案第1页,共2页
(知识讲解)
【非共顶点双垂线等角模型】
【双垂线共顶点等角模型】
【双垂线共顶点等角模型拓展】
【典型例题】
类型一、非共顶点双垂线等角模型
1.如图,在中,CD是斜边AB上的高.
求证:.
举一反三
【变式1】
2.(1)问题情境:如图1,Rt中,∠ACB=90°,CD⊥AB,我们可以利用与相似证明AC2=AD AB,这个结论我们称之为射影定理,试证明这个定理.
(2)结论运用:如图2,正方形ABCD的边长为6,点O是对角线AC,BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,试利用射影定理证明.
【变式2】
3.【问题情境】如图1,在中,,垂足为D,我们可以得到如下正确结论:①;②;③,这些结论是由古希酷著名数学家欧几里得在《几何原本》最先提出的,我们称之为“射影定理”,又称“欧几里德定理”.
(1)请证明“射影定理”中的结论③.
(2)【结论运用】如图2,正方形的边长为6,点O是对角线、的交点,点E在上,过点C作,垂足为F,连接.
①求证:.
②若,求的长.
类型二、双垂线共顶点等角模型
4.如图,已知CD为Rt△ABC斜边上的中线,过点D作AC的平行线,过点C作CD的垂线,两线相交于点E. 求证:△ABC∽△DEC.
举一反三
【变式1】
5.如图,在矩形中,,点E是边上的任一点(不包括端点D,C),过点A作交的延长线于点F,设.
(1)求的长(用含a的代数式表示);
(2)连接交于点G,连接,当时,求证:四边形是菱形.
【变式2】
6.如图①,在正方形中,,为对角线上任意一点(不与重合),连接,过点作,交线段于点.
(1)求证:;
(2)若,求证:;
(3)如图②,连接交于点.若,求的值.
类型三、双垂线共顶点等角模型拓展
7.如图,已知∠EAC=∠DAB,∠D=∠B,求证:△ABC∽△ADE.
举一反三
【变式1】
8.(1)已知线段线段c是线段和b的比例中项,求线段c的长.
(2)如图所示,在和中,.
①写出图中两对相似三角形(不得添加字母和线).
②请写出其中一对三角形相似理由.
【变式2】
9.如图,D为△ABC内一点,E为△ABC外一点,且∠ABC=∠DBE,∠3=∠4.
求证:(1)△ABD∽△CBE;
(2)△ABC∽△DBE.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.见解析
【分析】根据两个角相等的两个三角形相似进行证明即可.
【详解】证明:如图,
∵在中,CD是斜边AB上的高
∴
∵是公共角
∴.
【点睛】本题考查了相似三角形的判定,解题关键是熟练掌握相似三角形的判定定理,准确运用进行推理证明.
2.(1)见解析;(2)见解析.
【分析】(1)由AA证明,再结合相似三角形对应边成比例即可解题;
(2)根据正方形的性质及射影定理解得BC2=BO BD,BC2=BF BE,再运用SAS证明△BOF∽△BED即可.
【详解】证明:(1)如图1,
(2)如图2,
∵四边形ABCD为正方形,
∴OC⊥BO,∠BCD=90°,
∴BC2=BO BD,
∵CF⊥BE,
∴BC2=BF BE,
∴BO BD=BF BE,即,
而∠OBF=∠EBD,
∴△BOF∽△BED.
【点睛】本题考查射影定理、相似三角形的判定与性质、正方形的性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.
3.(1)见解析;
(2)①见解析;②.
【分析】(1)由AA证明,再由相似三角形对应边称比例得到,继而解题;
(2)①由“射影定理”分别解得,,整理出,再结合即可证明;
②由勾股定理解得,再根据得到,代入数值解题即可.
【详解】(1)证明:
(2)①四边形ABCD是正方形
②在中,
在,
.
【点睛】本题考查相似三角形的综合题,涉及勾股定理、正方形等知识,是重要考点,掌握相关知识是解题关键.
4.见解析
【分析】根据直角三角形斜边上的中线等于斜边的一半可得出CD=AD,进而可得出∠A=∠ACD,由平行线的性质可得出∠CDE=∠ACD=∠A,再结合∠ACB=∠DCE=90°,即可证出△ABC∽△DEC.
【详解】∵CD为Rt△ABC斜边上的中线,
∴.
∴.
∵DE∥AC.
∴.
∴.
∵,CE⊥CD,
∴ .
∴△ABC∽△DEC.
【点睛】本题考查相似三角形的判定与性质,直角三角形斜边上的中线,解题关键是找出证明三角形相似的条件.
5.(1)
(2)见详解
【分析】(1)根据矩形的性质可得,然后可证,进而根据相似三角形的性质可求解;
(2)如图,连接AC,由题意易证四边形是平行四边形,然后可得,进而可证,则可证,最后问题可求证.
【详解】(1)解:∵四边形是矩形,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵,,
∴;
(2)证明:由题意可得如图所示:
连接AC,
在矩形中,,,
∴,
∵,
∴四边形是平行四边形,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴四边形是菱形.
【点睛】本题主要考查相似三角形的性质与判定、矩形的性质及菱形的判定,熟练掌握相似三角形的性质与判定、矩形的性质及菱形的判定是解题的关键.
6.(1)见解析;(2)见解析;(3).
【分析】(1)如图,过分别作交于点,交于点,则四边形是平行四边形,先证明四边形是正方形,继而证明,即可得结论;
(2)由(1)得,,根据比例线段可得,,再根据可得,从而求得AN、BN长即可得结论;
(3)把绕点逆时针旋转得到,连接,,进而可推导得出,,证明是等腰直角三角形,继而证明,可得MG=HG,根据题意设,则,根据勾股定理可求得,再结合正方形的性质可求得a的值,继而证明, 根据相似三角形的性质即可求得答案.
【详解】(1)如图,过分别作交于点,交于点,则四边形是平行四边形,
四边形是正方形,
,,
,
平行四边形是正方形,
,
,
,
,
,
,
;
(2)由(1)得:,,
,
,,
,
,
,,
;
(3)把绕点逆时针旋转得到,连接,
,,
,,,.
,,
,,
是等腰直角三角形,
,
,
,
,
,
设,则,
在中,,则,
正方形的边长为,
,
,
,
,,
,,
,
,
.
【点睛】本题考查的是四边形的综合题,涉及了正方形判定与性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理等知识,综合性较强,正确把握相关的判定定理与性质定理是解题的关键.
7.见解析
【分析】由∠EAC=∠DAB,可推出∠BAC=∠DAE,再由∠B=∠D,即可证明△ABC∽△ADE.
【详解】解:∵∠EAC=∠DAB,
∴∠EAC+∠DAC=∠DAB+∠DAC,即∠BAC=∠DAE,
又∵∠B=∠D,
∴△ABC∽△ADE.
【点睛】本题主要考查了相似三角形的判定,熟知相似三角形的判定条件是解题的关键.
8.(1)6cm;(2)①△ABC∽△ADE,△ABD∽△ACE;②见解析
【分析】(1)根据线段比例中项的概念得出a:c=c:b,再根据a=4cm,b=9cm,求出c的值,注意把负值舍去.
(2)①根据有两组对角对应相等的三角形相似可得出△ABC∽△ADE,再由两组对应边的比相等且夹角对应相等的两个三角形相似可得出△ABD∽△ACE;
②由①中可得对应线段成比例,又根据其对应角相等,即可判定其相似.
【详解】解:(1)∵线段c是线段a和b的比例中项,a=4cm,b=9cm,
∴c2=ab=36,
解得:c=±6,
又∵线段是正数,
∴c=6cm.
(2)①由题意可得:△ABC∽△ADE,△ABD∽△ACE;
②证明:∵,
∴∠BAD+∠CAD=∠CAE+∠CAD,即∠BAC=∠DAE,
又∵,
∴△ABC∽△ADE,
∴,
∴AB×AE=AC×AD,
∴,
∵∠BAD=∠CAE,
∴△ABD∽△ACE.
【点睛】本题考查的是相似三角形的判定,熟记相似三角形的判定定理是解答此题的关键.
9.(1)证明见解析;(2)证明见解析;
【分析】(1)根据有两组角对应相等的两个三角形相似可判断△ABD∽△CBE;
(2)先利用得到∠1=∠2得到∠ABC=∠DBE,再利用△ABD∽△CBE得 , 根据比例的性质得到 , 然后根据两组对应边的比相等且夹角对应相等的两个三角形相似可判断△ABC与△DBE相似.
【详解】(1)相似.理由如下:
∵∠1=∠2,∠3=∠4.
∴△ABD∽△CBE;
(2)相似.理由如下:
∵∠1=∠2,
∴∠1+∠DBC=∠2+DBC,即∠ABC=∠DBE,
∵△ABD∽△CBE,
∴=,
∴=,
∴△ABC∽△DBE.
【点睛】本题考查了三角形相似的判定,熟练掌握三角形相似的判定方法是解题关键.
答案第1页,共2页
答案第1页,共2页
