专题28.5特殊角的三角函数 专项练习(含解析)2023-2024学年九年级数学下册人教版专项讲练
文档属性
| 名称 | 专题28.5特殊角的三角函数 专项练习(含解析)2023-2024学年九年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 18:55:23 | ||
图片预览



文档简介
专题28.5 特殊角的三角函数(专项练习)
一、单选题
1.tan45°=( )
A.1 B. C. D.
2.下列三角函数的值是的是( ).
A. B. C. D.
3.点关于y轴对称的点的坐标是( ).
A. B.
C. D.
4.已知,则锐角α的度数是( )
A.60° B.45° C.30° D.75°
5.在△ABC中,∠C=90°,AB=,BC=1,则∠A的度数为( )
A. B. C. D.
6.关于三角函数有如下的公式:,由该公式可求得的值是( )
A. B. C. D.
7.若,则ABC的形状是( )
A.含有60°直角三角形 B.等边三角形
C.含有60°的任意三角形 D.等腰直角三角形
8.在实数,x0(x≠0),cos30°,中,有理数的个数是( )
A.1个 B.2个 C.3个 D.4个
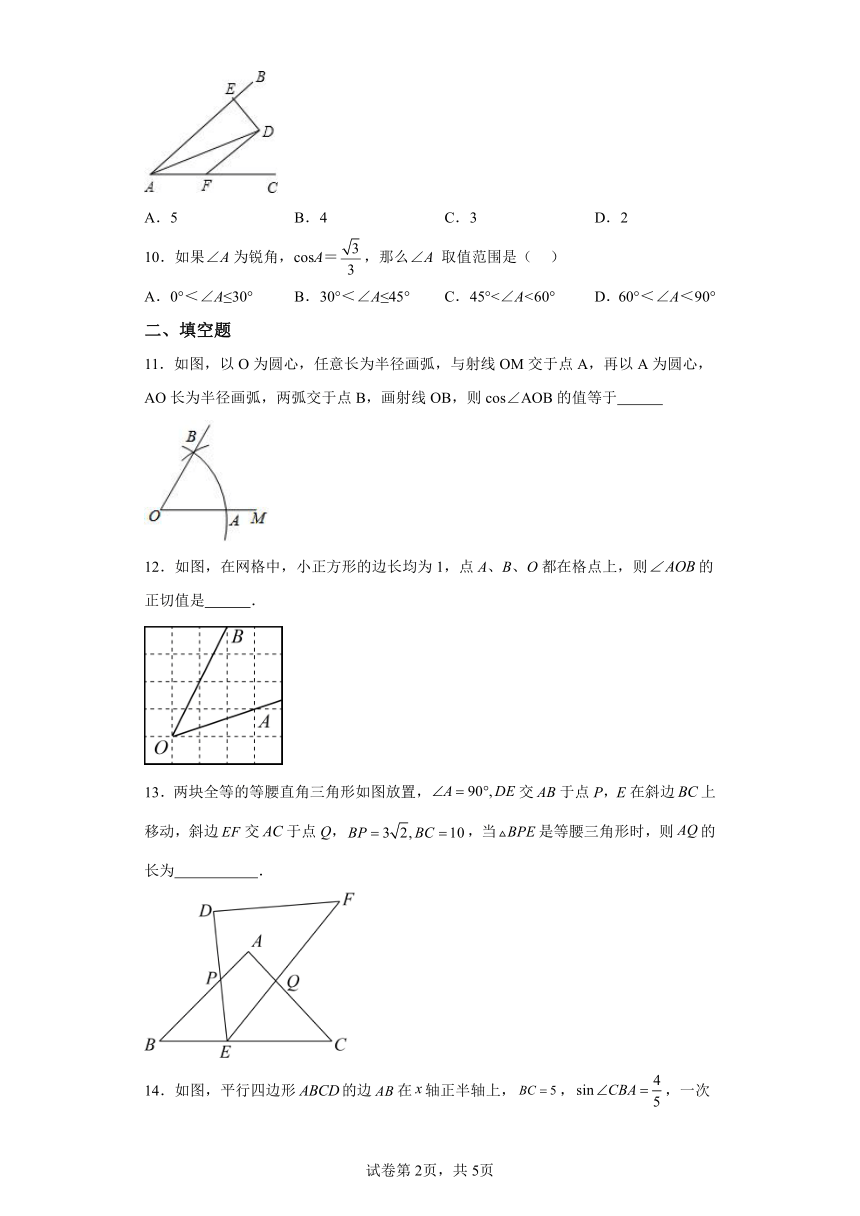
9.如图,,平分,于E,,已知,则( )
A.5 B.4 C.3 D.2
10.如果∠A为锐角,cosA=,那么∠A 取值范围是( )
A.0°<∠A≤30° B.30°<∠A≤45° C.45°<∠A<60° D.60°<∠A<90°
二、填空题
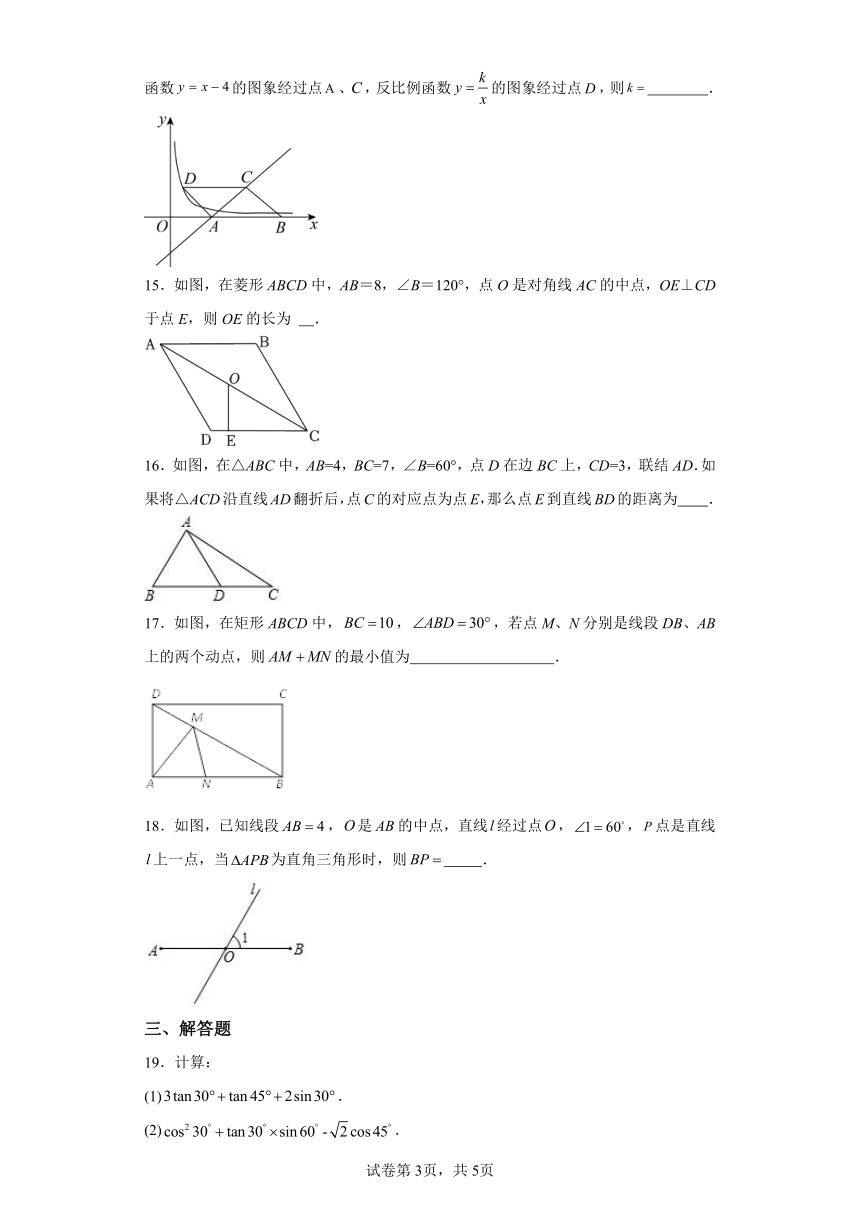
11.如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则cos∠AOB的值等于
12.如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则的正切值是 .
13.两块全等的等腰直角三角形如图放置,交于点P,E在斜边上移动,斜边交于点Q,,当是等腰三角形时,则的长为 .
14.如图,平行四边形的边在轴正半轴上,,,一次函数的图象经过点、,反比例函数的图象经过点,则 .
15.如图,在菱形ABCD中,AB=8,∠B=120°,点O是对角线AC的中点,OE⊥CD于点E,则OE的长为 .
16.如图,在△ABC中,AB=4,BC=7,∠B=60°,点D在边BC上,CD=3,联结AD.如果将△ACD沿直线AD翻折后,点C的对应点为点E,那么点E到直线BD的距离为 .
17.如图,在矩形ABCD中,,,若点M、N分别是线段DB、AB上的两个动点,则的最小值为 .
18.如图,已知线段,是的中点,直线经过点,,点是直线上一点,当为直角三角形时,则 .
三、解答题
19.计算:
(1).
(2).
20.计算
(1).
(2).
21.计算与化简题
(1)计算:
(2)先化简,再求代数式的值,其中.
22.如图,已知等边三角形ABC的边长为6cm,点P从点A出发,沿A→C→B的方向以2cm/s的速度向终点B运动,同时点Q从点B出发,沿B→A的方向以1cm/s的速度向终点A运动.当点P运动到点B时,两点均停止运动.运动时间记为,请解决下列问题:
(1)若点P在边AC上,当为何值时,APQ为直角三角形?
(2)是否存在这样的值,使APQ的面积为cm2 ?若存在,请求出的值,若不存在,请说明理由.
23.四边形ABCD是菱形,∠ABC=60°,E是对角线BD上的一个动点,连接AE,将线段AE绕点A逆时针旋转120°得到线段AF,连接EF,DF.
(1)如图1,求∠BDF的度数;
(2)如图2,当DB=3DF时,连接EC,求证:四边形FECD是矩形;
(3)若G为DF中点,连接EG,当线段BD与DF满足怎样的数量关系时,四边形AEGF是菱形,并说明理由.
24.如图,抛物线y=ax2+bx+c经过点A(﹣2,5),与x轴相交于B(﹣1,0),C(3,0)两点.
(1)求抛物线的函数表达式;
(2)点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△BC′D,若点C′恰好落在抛物线的对称轴上,求点C′和点D的坐标;
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据直角三角形中45°角的正切值计算并判断即可.
【详解】解:tan45°=1,
故选:A.
【点睛】本题考查直角三角形中45°角的正切值,能够牢记直角三角形中特殊度数的角的正切值,正弦值,余弦值是解决此类题型的关键.
2.A
【分析】根据特殊角的三角函数值解答.
【详解】A、=,符合题意;
B、=,不符合题意;
C、=,不符合题意;
D、=,不符合题意;
故选A.
【点睛】本题考查特殊角的三角函数值,准确掌握常见的特殊角的三角函数值是解题的关键.
3.C
【分析】先利用特殊角的三角函数值得出点的坐标,再写出其关于y轴对称的坐标即可.
【详解】解:∵sin60°=,cos30°=,
∴点(,)关于y轴对称的点的坐标是(,).
故选:C.
【点睛】本题考查了特殊角的三角函数值和关于坐标轴对称的点的特征,掌握特殊角的三角函数值是解决本题的关键.
4.A
【分析】根据得到即可求解.
【详解】解:∵,为锐角,
∴,
∴,
故选:A.
【点睛】本题考查根据特殊角三角函数值求角的度数,熟记特殊角的三角函数值是解答的关键.
5.B
【分析】直接利用已知画出直角三角形,再利用锐角三角函数关系得出答案.
【详解】解:∵∠C=90°,AB=,BC=1,
∴sinA=,
∴∠A=45°.
故选:B.
【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.
6.B
【分析】根据,代入特殊三角函数值计算即可.
【详解】解:
,
故选:B.
【点睛】本题考查了实数的运算,特殊角的三角函数值,灵活运用公式把一般角转化为特殊角的和或者差是解题的关键.
7.A
【分析】根据绝对值和平方的非负性,可得,从而得到,即可求解.
【详解】解∶∵,
∴,
解得:,
∴,
∴∠C=90°,
∴ABC是含有60°直角三角形.
故选:A
【点睛】本题主要考查了特殊角锐角三角函数值,绝对值和平方的非负性,熟练掌握特殊角锐角三角函数值是解题的关键.
8.B
【分析】根据零指数幂,特殊角的三角函数值,实数的意义,即可解答.
【详解】解:在实数,x0(x≠0)=1,,中,有理数是,x0=1,
所以,有理数的个数是2,
故选:B.
【点睛】本题考查了零指数幂,特殊角的三角函数值,实数,熟练掌握这些数学概念是解题的关键.
9.B
【分析】由角平分线的定义和平行线的性质易得,作于,根据角平分线的性质可得,,在中,易得,即可求得.
【详解】解:作于,
∵平分,
∴,
∵,
∴,
∴,
∴,
∴中,,
∴.
故选:B.
【点睛】此题主要考查角平分线、平行线的性质和直角三角形中角所对直角边等于斜边的一半,作辅助线是关键.
10.C
【分析】分别求出60°和45°角的余弦值,由此得到答案.
【详解】∵cos60°=,cos45°=,且
∴45°<∠A<60°.
故选C.
【点睛】此题考查了角度的余弦公式,余弦值随着角度的增大而减小的性质,熟记公式是解题的关键.
11.
【详解】∵OA=OB=AB,
∴△ABC是等边三角形,
∴∠AOB=60°,
∴cos∠AOB=cos60°=.
故答案是:.
12.1
【分析】连接AB,由勾股定理求得AB、AO、BO的长,判断△ABO是等腰直角三角形,即可求得答案.
【详解】解:连接AB,
由勾股定理得:AB=,AO=,OB=,
∴AB=AO,,
∴△ABO是以OB为斜边的等腰直角三角形,
∴,
故答案为:1.
【点睛】此题考查了勾股定理在网格中的应用、勾股定理的逆定理、等腰直角三角形的性质、特殊角的三角函数值等知识,熟练掌握勾股定理及其逆定理是解题的关键.
13.或或
【分析】解答时,分BE=PE,PB=PE和BP=BE三种情况求解即可.
【详解】解:当BE=PE时,
∵∠B=∠C=∠DEF=∠DFE=45°,
∴∠BPE=45°,∠BEP=90°,∠QEC=45°,∠EQC=90°,
∴PE=BE=BPsin45°=,EQ=CQ=ECsin45°=,
∵ BC=10,
∴AC=BCsin45°=,
∴AQ=AC-QC=.
当PB=PE时,
根据前面计算,得到BH=PH=3,
∴BH=HE=3,
∵∠B=∠C=∠DEF=∠DFE=45°,
∴∠EQC=45°,∠CEQ=90°,EC=EQ=BC-BE=10-6=4,
∴CQ=,
∵ BC=10,
∴AC=BCsin45°=,
∴AQ=AC-QC=.
当BP=BE时,
∵∠B=∠C=∠DEF=∠DFE=45°,
∴∠BPE=∠BEP=∠QEC=∠EQC,
∴PE=BE=,EQ=CQ=BC-BE=,
∵ BC=10,
∴AC=BCsin45°=,
∴AQ=AC-QC=,
综上所述AQ的长为或或,
故答案为:或或.
【点睛】本题考查了等腰直角三角形的性质,勾股定理,等腰三角形的判定和性质,特殊角的三角函数值,熟练掌握等腰直角三角形的性质和准确进行等腰三角形的等腰分类,灵活运用特殊角的三角函数值是解题的关键.
14.4
【分析】根据平行四边形的性质、三角函数值,结合一次函数求出D的坐标即可求解;
【详解】解:如图,过点D作DE⊥AB
将y=0代入y=x-4中
记得x=4
∴A(4,0)
在平行四边形ABCD中,
∵∠OAD=∠CBA
∴
∵AD=BC=5
∴DE=4,AE=3
∴OE=OA-AE=4-3=1
∴D(1,4)
∴
故答案为:4
【点睛】本题主要考查反比例函数、平行四边形、三角函数值、一次函数,掌握相关知识并灵活应用是解题的关键.
15.
【分析】连接OB,由菱形的性质得BC=AB=8,BO⊥AC,再由等腰三角形的性质得∠ACB=∠ACD=30°,然后由锐角三角函数定义求出OC=4,最后由含30°角的直角三角形的性质求解即可.
【详解】解:连接OB,如图所示:
∵四边形ABCD为菱形,点O是对角线AC的中点,
∴BC=AB=8,BO⊥AC,
∴∠ACB=∠ACD(180°﹣120°)=30°,
在Rt△BOC中,OC=cos30° BC8=4,
∵OE⊥CD,
∴∠CEO=90°,
在Rt△COE中,OEOC42,
故答案为:2.
【点睛】本题考查了菱形的性质、等腰三角形的性质、锐角三角函数定义以及含30°角的直角三角形的性质,解题的关键是熟练掌握菱形的性质.
16..
【分析】过E点作EH⊥BC于H,证明△ABD是等边三角形,进而求得∠ADC=120°,再由折叠得到∠ADE=∠ADC=120°,进而求出∠HDE=60°,最后在Rt△HED中使用三角函数即可求出HE的长.
【详解】解:如图,过点E作EH⊥BC于H,
∵BC=7,CD=3,
∴BD=BC-CD=4,
∵AB=4=BD,∠B=60°,
∴△ABD是等边三角形,
∴∠ADB=60°,
∴∠ADC=∠ADE=120°,
∴∠EDH=60°,
∵EH⊥BC,∴∠EHD=90°.
∵DE=DC=3,
∴EH=DE×sin∠HDE=3×=,
∴E到直线BD的距离为.
故答案为:.
【点睛】本题考查了折叠问题,解直角三角形,点到直线的距离,本题的关键点是能求出∠ADE=∠ADC=120°,另外需要重点掌握折叠问题的特点:折叠前后对应的边相等,对应的角相等.
17.
【分析】如图,过A作于,延长,使,过作于,交于,则最短,再利用矩形的性质与锐角三角函数求解即可得到答案.
【详解】解:如图,过A作于,延长,使,过作于,交于,则最短,
四边形为矩形,,,
即的最小值为
故答案为:
【点睛】本题考查的是矩形的性质,锐角三角函数的应用,同时考查利用轴对称与垂线段最短求线段和的最小值问题,解题的关键是掌握以上知识.
18.2或或.
【分析】分、、三种情况,根据直角三角形的性质、勾股定理计算即可.
【详解】解:如图:
∵,
∴当时,,
当时,∵,
∴,
∴,
当时,∵,
∴,
故答案为2或或.
【点睛】本题考查的是勾股定理,如果直角三角形的两条直角边长分别是,,斜边长为,那么.
19.(1)2
(2)
【分析】(1)根据特殊角的三角函数值解决此题.
(2)根据特殊角的三角函数值及二次根式的乘法进行计算即可解决此题.
【详解】(1)解:原式=31+2
1+1
2;
(2)解:原式=
1
.
【点睛】本题主要考查特殊角的三角函数值及二次根式的运算,熟练掌握特殊角的三角函数值是解决本题的关键.
20.(1)
(2)
【分析】(1)先化简绝对值、计算零指数幂与负整数指数幂、特殊角的正切值、立方根,再计算二次根式的乘法与加减法即可得;
(2)先计算特殊角的三角函数值,再计算二次根式的乘法与加减法即可得.
【详解】(1)解:原式
.
(2)解:原式
.
【点睛】本题考查了含特殊角的三角函数的混合运算、二次根式的乘法与加减法、零指数幂与负整数指数幂等知识点,熟记特殊角的三角函数值是解题关键.
21.(1)
(2),
【分析】(1)根据负整数指数幂,胡加绝对值,零次幂,特殊角的三角函数值,进行计算求解即可;
(2)先去括号,把除法变为乘法把分式化简,再把数代入求值.
【详解】(1)解:原式=
;
(2)
;
;
原式.
【点睛】本题考查了实数的混合运算,分式的化简求值,正确的计算是解题的关键.
22.(1)1.2或3
(2)存在,或4
【分析】(1)当APQ为直角三角形时,∠A=60度,所以可能只有∠APQ=90°或∠AQP=90°,当∠APQ=90°时,∠AQP=30°,AP=AQ,求出t=1.2秒;当∠AQP=90°时,∠APQ=30°,AQ=AP,求得t=3秒;
(2)当点P在AC上时,边AQ=6-t,算出AQ上的高PD=,即可写出(6-)●=,求得t=3-;当点P在BC上时,算出AQ边上的高PF=,即可写出(6-)●=,求得t=4.
【详解】(1)解:∵△ABC是等边三角形,
∴AB=BC=CA=6,∠A=∠B=∠C=60°,
当点P在边AC上时,由题意知,AP=2,AQ=6-,
当∠APQ=90°时,AP=AQ,即2=(6-),解得=1.2,
当∠AQP=90°时,AQ=AP,即6-=×2,解得=3,
所以,点P在边AC上,当为1.2s或3s时,△APQ为直角三角形;
(2)存在
①当点P在边AC上时,此时0≤≤3,
过点P作PD⊥AB于点D,
在Rt△APD中,∠A=60°,AP=2,
∴sinA=,即sin60°==,
∴PD=,S△APQ=AQ●PD=(6-)●,
由(6-)●=,得(不合题意,舍去),;
②当点P在边BC上时,此时3≤≤6,
如图,过点P作PF⊥AB于点F,
在Rt△BPF中,∠B=60°,BP=12-2,
∴sinB=,即sin60°==,
∴PF=,S△APQ=AQ●PF=(6-)●,
由(6-)●=得
因此,当t为s或4s时,△APQ的面积为.
【点睛】本题主要考查了直角三角形的存在性和三角形的面积的存在性,解决问题的关键是熟练掌握直角三角形的直角三个角都有可能,要分类讨论;面积是同一个值的三角形不可能只有一个,全面考虑,分类讨论.
23.(1);(2)证明见解析;(3),理由见解析
【分析】(1)先证明可得再证明 从而可得答案;
(2) 先证明 再证明 从而可得结论;
(3)先证明 结合 可得 从而可得答案.
【详解】解(1) 四边形ABCD是菱形,∠ABC=60°,
,
由旋转可得:
又∵四边形ABCD是菱形,
又∵四边形ABCD是菱形,
(2)由(1)可得:
由(1)可得:
是直角三角形,
由菱形的对称性可得:
而
四边形为矩形.
(3) 理由如下:如图,
四边形是菱形,
【点睛】本题考查的是旋转的性质,全等三角形的判定与性质,菱形的性质,锐角三角函数的应用,灵活的应用以上知识解题是解题的关键.
24.(1)y=x2﹣2x﹣3;(2)点C′的坐标为(1,2),点D的坐标为(1,)
【分析】(1)根据抛物线经过点,与轴相交于,两点,利用待定系数法求得该抛物线的解析式即可;
(2)先确定二次函数对称轴,BC长度,根据题意和翻折的性质,得到B C′长度,利用三角函数求出∠C′BC,再根据角平分线求出∠DBC,解直角三角形可以求得点和点的坐标,本题得以解决.
【详解】解:(1)∵抛物线y=ax2+bx+c经过点A(﹣2,5),与x轴相交于B(﹣1,0),C(3,0)两点,
∴,得,
即抛物线的函数表达式是y=x2﹣2x﹣3;
(2)∵与x轴相交于B(﹣1,0),C(3,0)两点,
∴BC=3﹣(﹣1)=3+1=4,该抛物线的对称轴是直线x==1,
设抛物线的对称轴与x轴的交点为H,
则点H的坐标为(1,0),
∴BH=2,
∵将△BCD沿直线BD翻折得到△BC′D,点C′恰好落在抛物线的对称轴上,
∴BC=BC′=4,∠C′HB=90°,∠C′BD=∠DBC,
∴OC′==2,cos∠C′BH===,
∴C′的坐标为(1,2),∠C′BH=60°,
∴∠DBC=30°,
∵BH=2,∠DBH=30°,
∴OD=BH tan30°=2×=,
∴点D的坐标为(1,),
由上可得,点C′的坐标为(1,2),点D的坐标为(1,).
【点睛】本题考查待定系数法求抛物线解析式,图形翻折变化、二次函数的性质、特殊角的三角函数值,解答本题的关键是明确题意,利用数形结合的思想解答.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.tan45°=( )
A.1 B. C. D.
2.下列三角函数的值是的是( ).
A. B. C. D.
3.点关于y轴对称的点的坐标是( ).
A. B.
C. D.
4.已知,则锐角α的度数是( )
A.60° B.45° C.30° D.75°
5.在△ABC中,∠C=90°,AB=,BC=1,则∠A的度数为( )
A. B. C. D.
6.关于三角函数有如下的公式:,由该公式可求得的值是( )
A. B. C. D.
7.若,则ABC的形状是( )
A.含有60°直角三角形 B.等边三角形
C.含有60°的任意三角形 D.等腰直角三角形
8.在实数,x0(x≠0),cos30°,中,有理数的个数是( )
A.1个 B.2个 C.3个 D.4个
9.如图,,平分,于E,,已知,则( )
A.5 B.4 C.3 D.2
10.如果∠A为锐角,cosA=,那么∠A 取值范围是( )
A.0°<∠A≤30° B.30°<∠A≤45° C.45°<∠A<60° D.60°<∠A<90°
二、填空题
11.如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则cos∠AOB的值等于
12.如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则的正切值是 .
13.两块全等的等腰直角三角形如图放置,交于点P,E在斜边上移动,斜边交于点Q,,当是等腰三角形时,则的长为 .
14.如图,平行四边形的边在轴正半轴上,,,一次函数的图象经过点、,反比例函数的图象经过点,则 .
15.如图,在菱形ABCD中,AB=8,∠B=120°,点O是对角线AC的中点,OE⊥CD于点E,则OE的长为 .
16.如图,在△ABC中,AB=4,BC=7,∠B=60°,点D在边BC上,CD=3,联结AD.如果将△ACD沿直线AD翻折后,点C的对应点为点E,那么点E到直线BD的距离为 .
17.如图,在矩形ABCD中,,,若点M、N分别是线段DB、AB上的两个动点,则的最小值为 .
18.如图,已知线段,是的中点,直线经过点,,点是直线上一点,当为直角三角形时,则 .
三、解答题
19.计算:
(1).
(2).
20.计算
(1).
(2).
21.计算与化简题
(1)计算:
(2)先化简,再求代数式的值,其中.
22.如图,已知等边三角形ABC的边长为6cm,点P从点A出发,沿A→C→B的方向以2cm/s的速度向终点B运动,同时点Q从点B出发,沿B→A的方向以1cm/s的速度向终点A运动.当点P运动到点B时,两点均停止运动.运动时间记为,请解决下列问题:
(1)若点P在边AC上,当为何值时,APQ为直角三角形?
(2)是否存在这样的值,使APQ的面积为cm2 ?若存在,请求出的值,若不存在,请说明理由.
23.四边形ABCD是菱形,∠ABC=60°,E是对角线BD上的一个动点,连接AE,将线段AE绕点A逆时针旋转120°得到线段AF,连接EF,DF.
(1)如图1,求∠BDF的度数;
(2)如图2,当DB=3DF时,连接EC,求证:四边形FECD是矩形;
(3)若G为DF中点,连接EG,当线段BD与DF满足怎样的数量关系时,四边形AEGF是菱形,并说明理由.
24.如图,抛物线y=ax2+bx+c经过点A(﹣2,5),与x轴相交于B(﹣1,0),C(3,0)两点.
(1)求抛物线的函数表达式;
(2)点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△BC′D,若点C′恰好落在抛物线的对称轴上,求点C′和点D的坐标;
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据直角三角形中45°角的正切值计算并判断即可.
【详解】解:tan45°=1,
故选:A.
【点睛】本题考查直角三角形中45°角的正切值,能够牢记直角三角形中特殊度数的角的正切值,正弦值,余弦值是解决此类题型的关键.
2.A
【分析】根据特殊角的三角函数值解答.
【详解】A、=,符合题意;
B、=,不符合题意;
C、=,不符合题意;
D、=,不符合题意;
故选A.
【点睛】本题考查特殊角的三角函数值,准确掌握常见的特殊角的三角函数值是解题的关键.
3.C
【分析】先利用特殊角的三角函数值得出点的坐标,再写出其关于y轴对称的坐标即可.
【详解】解:∵sin60°=,cos30°=,
∴点(,)关于y轴对称的点的坐标是(,).
故选:C.
【点睛】本题考查了特殊角的三角函数值和关于坐标轴对称的点的特征,掌握特殊角的三角函数值是解决本题的关键.
4.A
【分析】根据得到即可求解.
【详解】解:∵,为锐角,
∴,
∴,
故选:A.
【点睛】本题考查根据特殊角三角函数值求角的度数,熟记特殊角的三角函数值是解答的关键.
5.B
【分析】直接利用已知画出直角三角形,再利用锐角三角函数关系得出答案.
【详解】解:∵∠C=90°,AB=,BC=1,
∴sinA=,
∴∠A=45°.
故选:B.
【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.
6.B
【分析】根据,代入特殊三角函数值计算即可.
【详解】解:
,
故选:B.
【点睛】本题考查了实数的运算,特殊角的三角函数值,灵活运用公式把一般角转化为特殊角的和或者差是解题的关键.
7.A
【分析】根据绝对值和平方的非负性,可得,从而得到,即可求解.
【详解】解∶∵,
∴,
解得:,
∴,
∴∠C=90°,
∴ABC是含有60°直角三角形.
故选:A
【点睛】本题主要考查了特殊角锐角三角函数值,绝对值和平方的非负性,熟练掌握特殊角锐角三角函数值是解题的关键.
8.B
【分析】根据零指数幂,特殊角的三角函数值,实数的意义,即可解答.
【详解】解:在实数,x0(x≠0)=1,,中,有理数是,x0=1,
所以,有理数的个数是2,
故选:B.
【点睛】本题考查了零指数幂,特殊角的三角函数值,实数,熟练掌握这些数学概念是解题的关键.
9.B
【分析】由角平分线的定义和平行线的性质易得,作于,根据角平分线的性质可得,,在中,易得,即可求得.
【详解】解:作于,
∵平分,
∴,
∵,
∴,
∴,
∴,
∴中,,
∴.
故选:B.
【点睛】此题主要考查角平分线、平行线的性质和直角三角形中角所对直角边等于斜边的一半,作辅助线是关键.
10.C
【分析】分别求出60°和45°角的余弦值,由此得到答案.
【详解】∵cos60°=,cos45°=,且
∴45°<∠A<60°.
故选C.
【点睛】此题考查了角度的余弦公式,余弦值随着角度的增大而减小的性质,熟记公式是解题的关键.
11.
【详解】∵OA=OB=AB,
∴△ABC是等边三角形,
∴∠AOB=60°,
∴cos∠AOB=cos60°=.
故答案是:.
12.1
【分析】连接AB,由勾股定理求得AB、AO、BO的长,判断△ABO是等腰直角三角形,即可求得答案.
【详解】解:连接AB,
由勾股定理得:AB=,AO=,OB=,
∴AB=AO,,
∴△ABO是以OB为斜边的等腰直角三角形,
∴,
故答案为:1.
【点睛】此题考查了勾股定理在网格中的应用、勾股定理的逆定理、等腰直角三角形的性质、特殊角的三角函数值等知识,熟练掌握勾股定理及其逆定理是解题的关键.
13.或或
【分析】解答时,分BE=PE,PB=PE和BP=BE三种情况求解即可.
【详解】解:当BE=PE时,
∵∠B=∠C=∠DEF=∠DFE=45°,
∴∠BPE=45°,∠BEP=90°,∠QEC=45°,∠EQC=90°,
∴PE=BE=BPsin45°=,EQ=CQ=ECsin45°=,
∵ BC=10,
∴AC=BCsin45°=,
∴AQ=AC-QC=.
当PB=PE时,
根据前面计算,得到BH=PH=3,
∴BH=HE=3,
∵∠B=∠C=∠DEF=∠DFE=45°,
∴∠EQC=45°,∠CEQ=90°,EC=EQ=BC-BE=10-6=4,
∴CQ=,
∵ BC=10,
∴AC=BCsin45°=,
∴AQ=AC-QC=.
当BP=BE时,
∵∠B=∠C=∠DEF=∠DFE=45°,
∴∠BPE=∠BEP=∠QEC=∠EQC,
∴PE=BE=,EQ=CQ=BC-BE=,
∵ BC=10,
∴AC=BCsin45°=,
∴AQ=AC-QC=,
综上所述AQ的长为或或,
故答案为:或或.
【点睛】本题考查了等腰直角三角形的性质,勾股定理,等腰三角形的判定和性质,特殊角的三角函数值,熟练掌握等腰直角三角形的性质和准确进行等腰三角形的等腰分类,灵活运用特殊角的三角函数值是解题的关键.
14.4
【分析】根据平行四边形的性质、三角函数值,结合一次函数求出D的坐标即可求解;
【详解】解:如图,过点D作DE⊥AB
将y=0代入y=x-4中
记得x=4
∴A(4,0)
在平行四边形ABCD中,
∵∠OAD=∠CBA
∴
∵AD=BC=5
∴DE=4,AE=3
∴OE=OA-AE=4-3=1
∴D(1,4)
∴
故答案为:4
【点睛】本题主要考查反比例函数、平行四边形、三角函数值、一次函数,掌握相关知识并灵活应用是解题的关键.
15.
【分析】连接OB,由菱形的性质得BC=AB=8,BO⊥AC,再由等腰三角形的性质得∠ACB=∠ACD=30°,然后由锐角三角函数定义求出OC=4,最后由含30°角的直角三角形的性质求解即可.
【详解】解:连接OB,如图所示:
∵四边形ABCD为菱形,点O是对角线AC的中点,
∴BC=AB=8,BO⊥AC,
∴∠ACB=∠ACD(180°﹣120°)=30°,
在Rt△BOC中,OC=cos30° BC8=4,
∵OE⊥CD,
∴∠CEO=90°,
在Rt△COE中,OEOC42,
故答案为:2.
【点睛】本题考查了菱形的性质、等腰三角形的性质、锐角三角函数定义以及含30°角的直角三角形的性质,解题的关键是熟练掌握菱形的性质.
16..
【分析】过E点作EH⊥BC于H,证明△ABD是等边三角形,进而求得∠ADC=120°,再由折叠得到∠ADE=∠ADC=120°,进而求出∠HDE=60°,最后在Rt△HED中使用三角函数即可求出HE的长.
【详解】解:如图,过点E作EH⊥BC于H,
∵BC=7,CD=3,
∴BD=BC-CD=4,
∵AB=4=BD,∠B=60°,
∴△ABD是等边三角形,
∴∠ADB=60°,
∴∠ADC=∠ADE=120°,
∴∠EDH=60°,
∵EH⊥BC,∴∠EHD=90°.
∵DE=DC=3,
∴EH=DE×sin∠HDE=3×=,
∴E到直线BD的距离为.
故答案为:.
【点睛】本题考查了折叠问题,解直角三角形,点到直线的距离,本题的关键点是能求出∠ADE=∠ADC=120°,另外需要重点掌握折叠问题的特点:折叠前后对应的边相等,对应的角相等.
17.
【分析】如图,过A作于,延长,使,过作于,交于,则最短,再利用矩形的性质与锐角三角函数求解即可得到答案.
【详解】解:如图,过A作于,延长,使,过作于,交于,则最短,
四边形为矩形,,,
即的最小值为
故答案为:
【点睛】本题考查的是矩形的性质,锐角三角函数的应用,同时考查利用轴对称与垂线段最短求线段和的最小值问题,解题的关键是掌握以上知识.
18.2或或.
【分析】分、、三种情况,根据直角三角形的性质、勾股定理计算即可.
【详解】解:如图:
∵,
∴当时,,
当时,∵,
∴,
∴,
当时,∵,
∴,
故答案为2或或.
【点睛】本题考查的是勾股定理,如果直角三角形的两条直角边长分别是,,斜边长为,那么.
19.(1)2
(2)
【分析】(1)根据特殊角的三角函数值解决此题.
(2)根据特殊角的三角函数值及二次根式的乘法进行计算即可解决此题.
【详解】(1)解:原式=31+2
1+1
2;
(2)解:原式=
1
.
【点睛】本题主要考查特殊角的三角函数值及二次根式的运算,熟练掌握特殊角的三角函数值是解决本题的关键.
20.(1)
(2)
【分析】(1)先化简绝对值、计算零指数幂与负整数指数幂、特殊角的正切值、立方根,再计算二次根式的乘法与加减法即可得;
(2)先计算特殊角的三角函数值,再计算二次根式的乘法与加减法即可得.
【详解】(1)解:原式
.
(2)解:原式
.
【点睛】本题考查了含特殊角的三角函数的混合运算、二次根式的乘法与加减法、零指数幂与负整数指数幂等知识点,熟记特殊角的三角函数值是解题关键.
21.(1)
(2),
【分析】(1)根据负整数指数幂,胡加绝对值,零次幂,特殊角的三角函数值,进行计算求解即可;
(2)先去括号,把除法变为乘法把分式化简,再把数代入求值.
【详解】(1)解:原式=
;
(2)
;
;
原式.
【点睛】本题考查了实数的混合运算,分式的化简求值,正确的计算是解题的关键.
22.(1)1.2或3
(2)存在,或4
【分析】(1)当APQ为直角三角形时,∠A=60度,所以可能只有∠APQ=90°或∠AQP=90°,当∠APQ=90°时,∠AQP=30°,AP=AQ,求出t=1.2秒;当∠AQP=90°时,∠APQ=30°,AQ=AP,求得t=3秒;
(2)当点P在AC上时,边AQ=6-t,算出AQ上的高PD=,即可写出(6-)●=,求得t=3-;当点P在BC上时,算出AQ边上的高PF=,即可写出(6-)●=,求得t=4.
【详解】(1)解:∵△ABC是等边三角形,
∴AB=BC=CA=6,∠A=∠B=∠C=60°,
当点P在边AC上时,由题意知,AP=2,AQ=6-,
当∠APQ=90°时,AP=AQ,即2=(6-),解得=1.2,
当∠AQP=90°时,AQ=AP,即6-=×2,解得=3,
所以,点P在边AC上,当为1.2s或3s时,△APQ为直角三角形;
(2)存在
①当点P在边AC上时,此时0≤≤3,
过点P作PD⊥AB于点D,
在Rt△APD中,∠A=60°,AP=2,
∴sinA=,即sin60°==,
∴PD=,S△APQ=AQ●PD=(6-)●,
由(6-)●=,得(不合题意,舍去),;
②当点P在边BC上时,此时3≤≤6,
如图,过点P作PF⊥AB于点F,
在Rt△BPF中,∠B=60°,BP=12-2,
∴sinB=,即sin60°==,
∴PF=,S△APQ=AQ●PF=(6-)●,
由(6-)●=得
因此,当t为s或4s时,△APQ的面积为.
【点睛】本题主要考查了直角三角形的存在性和三角形的面积的存在性,解决问题的关键是熟练掌握直角三角形的直角三个角都有可能,要分类讨论;面积是同一个值的三角形不可能只有一个,全面考虑,分类讨论.
23.(1);(2)证明见解析;(3),理由见解析
【分析】(1)先证明可得再证明 从而可得答案;
(2) 先证明 再证明 从而可得结论;
(3)先证明 结合 可得 从而可得答案.
【详解】解(1) 四边形ABCD是菱形,∠ABC=60°,
,
由旋转可得:
又∵四边形ABCD是菱形,
又∵四边形ABCD是菱形,
(2)由(1)可得:
由(1)可得:
是直角三角形,
由菱形的对称性可得:
而
四边形为矩形.
(3) 理由如下:如图,
四边形是菱形,
【点睛】本题考查的是旋转的性质,全等三角形的判定与性质,菱形的性质,锐角三角函数的应用,灵活的应用以上知识解题是解题的关键.
24.(1)y=x2﹣2x﹣3;(2)点C′的坐标为(1,2),点D的坐标为(1,)
【分析】(1)根据抛物线经过点,与轴相交于,两点,利用待定系数法求得该抛物线的解析式即可;
(2)先确定二次函数对称轴,BC长度,根据题意和翻折的性质,得到B C′长度,利用三角函数求出∠C′BC,再根据角平分线求出∠DBC,解直角三角形可以求得点和点的坐标,本题得以解决.
【详解】解:(1)∵抛物线y=ax2+bx+c经过点A(﹣2,5),与x轴相交于B(﹣1,0),C(3,0)两点,
∴,得,
即抛物线的函数表达式是y=x2﹣2x﹣3;
(2)∵与x轴相交于B(﹣1,0),C(3,0)两点,
∴BC=3﹣(﹣1)=3+1=4,该抛物线的对称轴是直线x==1,
设抛物线的对称轴与x轴的交点为H,
则点H的坐标为(1,0),
∴BH=2,
∵将△BCD沿直线BD翻折得到△BC′D,点C′恰好落在抛物线的对称轴上,
∴BC=BC′=4,∠C′HB=90°,∠C′BD=∠DBC,
∴OC′==2,cos∠C′BH===,
∴C′的坐标为(1,2),∠C′BH=60°,
∴∠DBC=30°,
∵BH=2,∠DBH=30°,
∴OD=BH tan30°=2×=,
∴点D的坐标为(1,),
由上可得,点C′的坐标为(1,2),点D的坐标为(1,).
【点睛】本题考查待定系数法求抛物线解析式,图形翻折变化、二次函数的性质、特殊角的三角函数值,解答本题的关键是明确题意,利用数形结合的思想解答.
答案第1页,共2页
答案第1页,共2页
