专题28.8解直角三角形 知识讲解(含解析)2023-2024学年九年级数学下册人教版专项讲练
文档属性
| 名称 | 专题28.8解直角三角形 知识讲解(含解析)2023-2024学年九年级数学下册人教版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 694.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 00:00:00 | ||
图片预览



文档简介
专题28.8 解直角三角形(知识讲解)
【学习目标】
1.了解解直角三角形的含义,会综合运用平面几何中有关直角三角形的知识和锐角三角函数的定义解直角三角形;
2.会运用有关解直角三角形的知识解决实际生活中存在的解直角三角形问题.
【要点梳理】
要点一、解直角三角形
在直角三角形中,由已知元素(直角除外)求未知元素的过程,叫做解直角三角形.
在直角三角形中,除直角外,一共有5个元素,即三条边和两个锐角.
设在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,则有:
①三边之间的关系:a2+b2=c2(勾股定理).
②锐角之间的关系:∠A+∠B=90°.
③边角之间的关系:
,,,
,,.
④,h为斜边上的高.
要点诠释:
(1)直角三角形中有一个元素为定值(直角为90°),是已知值.
(2)这里讲的直角三角形的边角关系指的是等式,没有包括其他关系(如不等关系).
(3)对这些式子的理解和记忆要结合图形,可以更加清楚、直观地理解.
要点二、解直角三角形的常见类型及解法
已知条件 解法步骤
Rt△ABC 两边 两直角边(a,b) 由求∠A,∠B=90°-∠A,
斜边,一直角边(如c,a) 由求∠A,∠B=90°-∠A,
一边 一 角 一直角边和一锐角 锐角、邻边(如∠A,b) ∠B=90°-∠A,,
锐角、对边(如∠A,a) ∠B=90°-∠A,,
斜边、锐角(如c,∠A) ∠B=90°-∠A,,
要点诠释:
1.在遇到解直角三角形的实际问题时,最好是先画出一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的,然后按先确定锐角、再确定它的对边和邻边的顺序进行计算.
2.若题中无特殊说明,“解直角三角形”即要求出所有的未知元素,已知条件中至少有一个条件为边.
【典型例题】
类型一、解直角三角形
1.
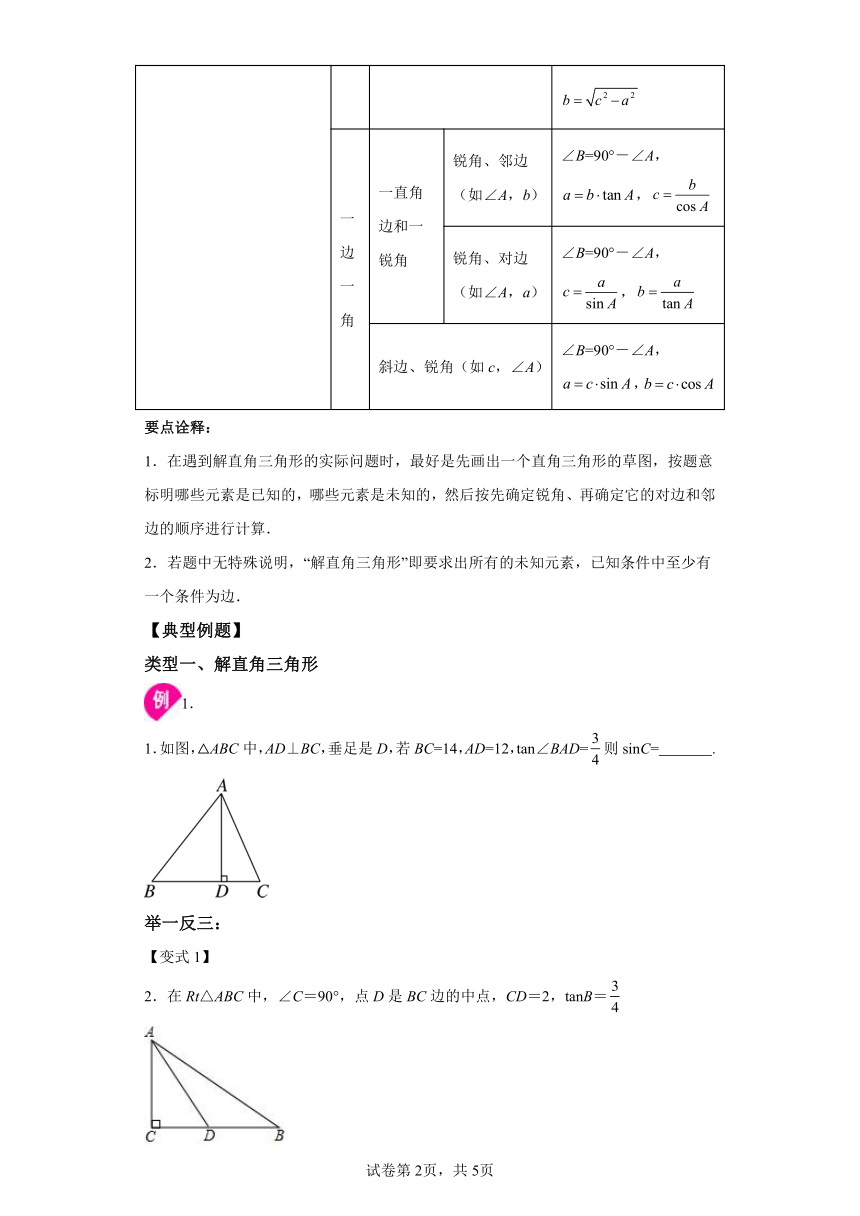
1.如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=则sinC= .
举一反三:
【变式1】
2.在Rt△ABC中,∠C=90°,点D是BC边的中点,CD=2,tanB=
(1)求AD和AB的长;
(2)求∠B的正弦、余弦值.
【变式2】
3.如图,已知Rt△ABC 中,∠C=90°,AD为∠BAC的平分线,且AD=2,AC=,解这个直角三角形.
类型二、解非直角三角形
2.
4.如图,在中,,,,求的面积.
举一反三:
【变式1】
5.如图,一艘货船以20n mile/h的速度向正南方向航行,在A处测得灯塔B在南偏东方向,航行5h后到达C处,测得灯塔B在北偏东方向,求C处距离灯塔B的距离BC(结果精确到0.1,参考数据:,,,).
【变式2】
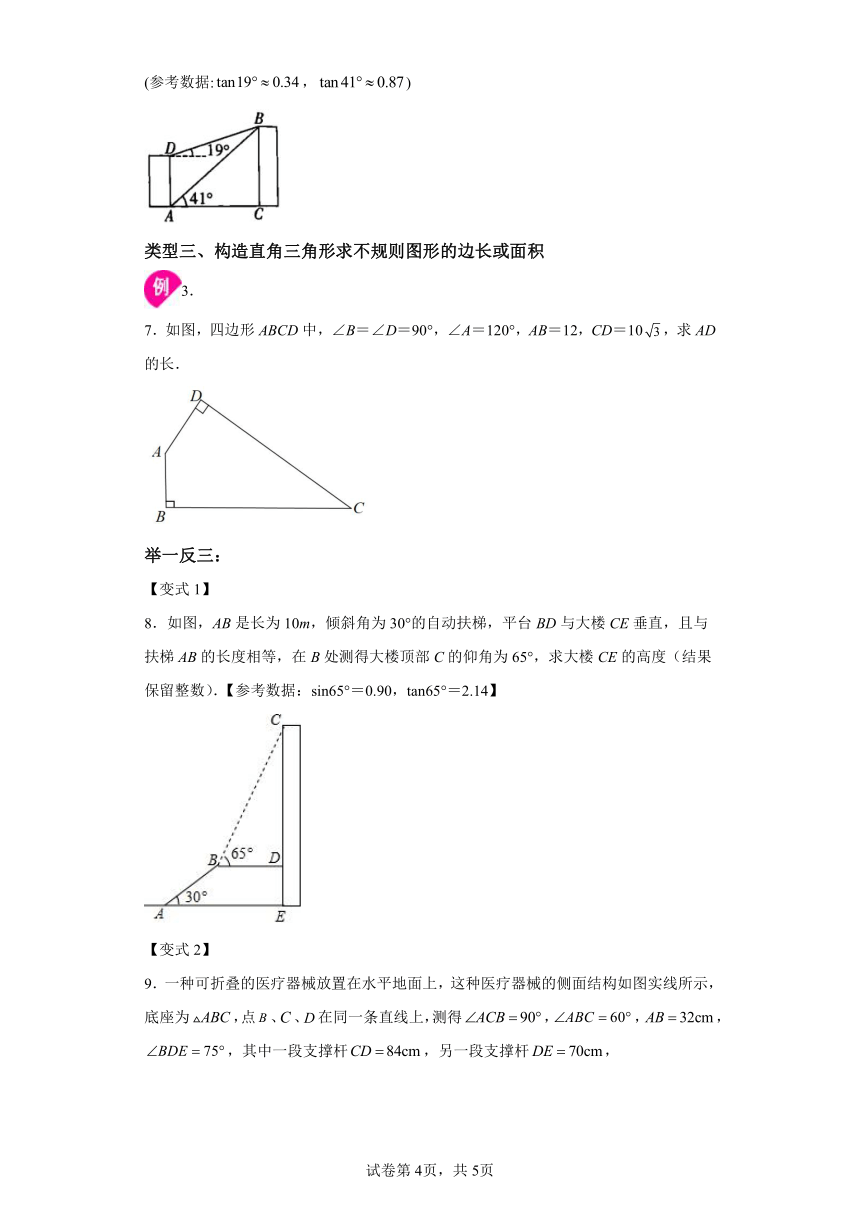
6.如图,已知一居民楼前方处有一建筑物,小敏在居民楼的顶部处和底部处分别测得建筑物顶部的仰角为和,求居民楼的高度和建筑物的高度(结果取整数).
(参考数据:,)
类型三、构造直角三角形求不规则图形的边长或面积
3.
7.如图,四边形ABCD中,∠B=∠D=90°,∠A=120°,AB=12,CD=10,求AD的长.
举一反三:
【变式1】
8.如图,AB是长为10m,倾斜角为30°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).【参考数据:sin65°=0.90,tan65°=2.14】
【变式2】
9.一种可折叠的医疗器械放置在水平地面上,这种医疗器械的侧面结构如图实线所示,底座为,点、、在同一条直线上,测得,,,,其中一段支撑杆,另一段支撑杆,
(1)求的距离;
(2)求支撑杆上的到水平地面的距离是多少?(用四舍五入法对结果取整数,参考数据,,,)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.
【分析】解Rt△ABD,根据AD=12,tan∠BAD=,求得BD=9,那么CD=5,再利用勾股定理即可求出AC,在Rt△ACD中,利用三角函数,即可求出sinC的值.
【详解】∵AD⊥BC,
∴∠ADB=∠ADC=90°.
在Rt△ABD中,∵AD=12,tan∠BAD=,
∴BD=9,
∴CD=BC-BD=14-9=5,
∴AC=;
在Rt△ACD中,∠ADC=90°,AD=12,AC=13,
∴sinC=.
【点睛】此题考查了解直角三角形,勾股定理,锐角三角函数,求出BD是解本题的关键.
2.(1),AB=5
(2)
【分析】(1)先根据中点、∠B的正切求出BC、AC的长,再利用勾股定理求值即可;
(2)利用直角三角形的边角间关系可得结论.
【详解】(1)解:∵点D是BC边的中点,CD=2,
∴BC=4.
在Rt△ABC中,
∵tanB=,
∴AC=3.
在Rt△ADC中,
AD=,
AB=.
(2)解:在Rt△ABC中,
sinB=,cosB=.
【点睛】本题主要考查了解直角三角形,掌握勾股定理、直角三角形的边角间关系是解决本题的关键.
3.,,,.
【分析】先在中,利用锐角三角函数的定义求出,再利用角平分线的定义求出,然后利用直角三角形的两个锐角互余求出,再利用锐角三角函数的定义求出,的长,即可解答.
【详解】解:,,,
,
,
为的平分线,
,
,
,
,
,,,.
【点睛】本题考查了解直角三角形,角平分线的性质,熟练掌握锐角三角函数的定义是解题的关键.
4.
【分析】过点A作ADCB于点D,利用,,勾股定理,结合三角形面积公式计算即可.
【详解】如图,过点A作ADCB于点D,
因为,AB=6,
所以,
所以=;
因为,AD=3,
所以DC=3AD=9,
所以的面积为:=.
【点睛】本题考考查了化斜为直解直角三角形,勾股定理,熟练掌握解直角的基本方法,灵活选择三角函数是解题的关键.
5.65.4nmile
【分析】过点B作,在Rt△CBH和Rt△BAH中,根据三角函数的定义即可计算出C处距离灯塔B的距离BC.
【详解】解:如图,过点B作,垂足为H,
由题意得,,,,
在Rt△CBH中,∵,,
∴,,
在Rt△BAH中,∵,
∴,
又∵,
∴,
所以,
∴.
答:BC的长约为65.4n mile.
【点睛】本题考查的是解直角三角形的应用,正确作出辅助线,把航海中的实际问题转化为解直角三角形的问题是解题的关键.
6.居民楼的高度AD约为16米,建筑物的高度BC约为26米.
【分析】通过作垂线,构造直角三角形,分别在Rt△BDE和RtABC中,根据锐角三角函数的意义求出BC、BE,进而求出AD,得出答案.
【详解】过点D作DE⊥BC于点E,则DE=AC=30,AD=EC,
由题意得,∠BDE=,∠BAC=41,
在Rt△ABC中,
BC=AC tan∠BAC=30×tan41≈26.1≈26,
在Rt△BDE中,
BE=DE tan∠BDE=30×tan19≈10.2,
∴AD=BC BE=26.1 10.2=15.9≈16.
答:居民楼的高度AD约为16米,建筑物的高度BC约为26米.
【点睛】考查直角三角形的边角关系,锐角三角函数,构造直角三角形利用锐角三角函数是解决问题的关键.
7.6
【分析】延长DA交CB的延长线于E,根据已知条件得到∠ABE=90°,根据邻补角的定义得到∠EAB=60°,得到∠E=30°,根据直角三角形的性质即可得到结论.
【详解】解:延长DA交CB的延长线于E,
∵∠ABC=90°,
∴∠ABE=90°,
∵∠DAB=120°,
∴∠EAB=60°,
∴∠E=30°,
∴AE=2AB=24,
∵∠D=90°,
∴∠C=60°,
∴DE= CD=30,
∴AD=DE-AE=6.
【点睛】本题考查了含30°角的直角三角形,正确的作出辅助线是解题的关键.
8.大楼CE的高度是26m.
【分析】作BF⊥AE于点F,根据三角函数的定义及解直角三角形的方法求出BF、CD即可.
【详解】解:作BF⊥AE于点F.则BF=DE.
在直角△ABF中,sin∠BAF=,则BF=AB sin∠BAF=10×=5(m).
在直角△CDB中,tan∠CBD=,则CD=BD tan65°=10×2.14=21.4(m).
则CE=DE+CD=BF+CD=5+21.4≈26(m).
答:大楼CE的高度是26m.
【点睛】此题主要考查解直角三角形,解题的关键是熟知三角函数的定义与性质.
9.(1)16cm
(2)105cm
【分析】(1)根据直角三角形中60°角解直角三角形即可;
(2)如图作DG⊥EF,,证明EF=EG+QC+CP,再分别运用解直角三角形求出EG、QC、CP即可.
【详解】(1)∵,,AB=32cm
∴(cm)
(2)如图,作DG⊥EF于点G,过点C作,交DG于点Q,交AB于点P,
∵DG⊥EF,AF⊥EF,
∴DG⊥PQ,AF⊥PQ,
∴四边形FPQG是矩形,FG=PQ,
∴(cm),(cm),
∵
∴∠EDG=75°-60°=15°
∴(cm)
∴EF=EG+FG=EG+PQ=EG+CQ+PC=(cm)
故E到地面的距离EF为105cm.
【点睛】本题主要考查解直角三角形,作辅助线构造相等线段,熟练运用解直角三角形求线段长度是解题关键.
答案第1页,共2页
答案第1页,共2页
【学习目标】
1.了解解直角三角形的含义,会综合运用平面几何中有关直角三角形的知识和锐角三角函数的定义解直角三角形;
2.会运用有关解直角三角形的知识解决实际生活中存在的解直角三角形问题.
【要点梳理】
要点一、解直角三角形
在直角三角形中,由已知元素(直角除外)求未知元素的过程,叫做解直角三角形.
在直角三角形中,除直角外,一共有5个元素,即三条边和两个锐角.
设在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,则有:
①三边之间的关系:a2+b2=c2(勾股定理).
②锐角之间的关系:∠A+∠B=90°.
③边角之间的关系:
,,,
,,.
④,h为斜边上的高.
要点诠释:
(1)直角三角形中有一个元素为定值(直角为90°),是已知值.
(2)这里讲的直角三角形的边角关系指的是等式,没有包括其他关系(如不等关系).
(3)对这些式子的理解和记忆要结合图形,可以更加清楚、直观地理解.
要点二、解直角三角形的常见类型及解法
已知条件 解法步骤
Rt△ABC 两边 两直角边(a,b) 由求∠A,∠B=90°-∠A,
斜边,一直角边(如c,a) 由求∠A,∠B=90°-∠A,
一边 一 角 一直角边和一锐角 锐角、邻边(如∠A,b) ∠B=90°-∠A,,
锐角、对边(如∠A,a) ∠B=90°-∠A,,
斜边、锐角(如c,∠A) ∠B=90°-∠A,,
要点诠释:
1.在遇到解直角三角形的实际问题时,最好是先画出一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的,然后按先确定锐角、再确定它的对边和邻边的顺序进行计算.
2.若题中无特殊说明,“解直角三角形”即要求出所有的未知元素,已知条件中至少有一个条件为边.
【典型例题】
类型一、解直角三角形
1.
1.如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=则sinC= .
举一反三:
【变式1】
2.在Rt△ABC中,∠C=90°,点D是BC边的中点,CD=2,tanB=
(1)求AD和AB的长;
(2)求∠B的正弦、余弦值.
【变式2】
3.如图,已知Rt△ABC 中,∠C=90°,AD为∠BAC的平分线,且AD=2,AC=,解这个直角三角形.
类型二、解非直角三角形
2.
4.如图,在中,,,,求的面积.
举一反三:
【变式1】
5.如图,一艘货船以20n mile/h的速度向正南方向航行,在A处测得灯塔B在南偏东方向,航行5h后到达C处,测得灯塔B在北偏东方向,求C处距离灯塔B的距离BC(结果精确到0.1,参考数据:,,,).
【变式2】
6.如图,已知一居民楼前方处有一建筑物,小敏在居民楼的顶部处和底部处分别测得建筑物顶部的仰角为和,求居民楼的高度和建筑物的高度(结果取整数).
(参考数据:,)
类型三、构造直角三角形求不规则图形的边长或面积
3.
7.如图,四边形ABCD中,∠B=∠D=90°,∠A=120°,AB=12,CD=10,求AD的长.
举一反三:
【变式1】
8.如图,AB是长为10m,倾斜角为30°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).【参考数据:sin65°=0.90,tan65°=2.14】
【变式2】
9.一种可折叠的医疗器械放置在水平地面上,这种医疗器械的侧面结构如图实线所示,底座为,点、、在同一条直线上,测得,,,,其中一段支撑杆,另一段支撑杆,
(1)求的距离;
(2)求支撑杆上的到水平地面的距离是多少?(用四舍五入法对结果取整数,参考数据,,,)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.
【分析】解Rt△ABD,根据AD=12,tan∠BAD=,求得BD=9,那么CD=5,再利用勾股定理即可求出AC,在Rt△ACD中,利用三角函数,即可求出sinC的值.
【详解】∵AD⊥BC,
∴∠ADB=∠ADC=90°.
在Rt△ABD中,∵AD=12,tan∠BAD=,
∴BD=9,
∴CD=BC-BD=14-9=5,
∴AC=;
在Rt△ACD中,∠ADC=90°,AD=12,AC=13,
∴sinC=.
【点睛】此题考查了解直角三角形,勾股定理,锐角三角函数,求出BD是解本题的关键.
2.(1),AB=5
(2)
【分析】(1)先根据中点、∠B的正切求出BC、AC的长,再利用勾股定理求值即可;
(2)利用直角三角形的边角间关系可得结论.
【详解】(1)解:∵点D是BC边的中点,CD=2,
∴BC=4.
在Rt△ABC中,
∵tanB=,
∴AC=3.
在Rt△ADC中,
AD=,
AB=.
(2)解:在Rt△ABC中,
sinB=,cosB=.
【点睛】本题主要考查了解直角三角形,掌握勾股定理、直角三角形的边角间关系是解决本题的关键.
3.,,,.
【分析】先在中,利用锐角三角函数的定义求出,再利用角平分线的定义求出,然后利用直角三角形的两个锐角互余求出,再利用锐角三角函数的定义求出,的长,即可解答.
【详解】解:,,,
,
,
为的平分线,
,
,
,
,
,,,.
【点睛】本题考查了解直角三角形,角平分线的性质,熟练掌握锐角三角函数的定义是解题的关键.
4.
【分析】过点A作ADCB于点D,利用,,勾股定理,结合三角形面积公式计算即可.
【详解】如图,过点A作ADCB于点D,
因为,AB=6,
所以,
所以=;
因为,AD=3,
所以DC=3AD=9,
所以的面积为:=.
【点睛】本题考考查了化斜为直解直角三角形,勾股定理,熟练掌握解直角的基本方法,灵活选择三角函数是解题的关键.
5.65.4nmile
【分析】过点B作,在Rt△CBH和Rt△BAH中,根据三角函数的定义即可计算出C处距离灯塔B的距离BC.
【详解】解:如图,过点B作,垂足为H,
由题意得,,,,
在Rt△CBH中,∵,,
∴,,
在Rt△BAH中,∵,
∴,
又∵,
∴,
所以,
∴.
答:BC的长约为65.4n mile.
【点睛】本题考查的是解直角三角形的应用,正确作出辅助线,把航海中的实际问题转化为解直角三角形的问题是解题的关键.
6.居民楼的高度AD约为16米,建筑物的高度BC约为26米.
【分析】通过作垂线,构造直角三角形,分别在Rt△BDE和RtABC中,根据锐角三角函数的意义求出BC、BE,进而求出AD,得出答案.
【详解】过点D作DE⊥BC于点E,则DE=AC=30,AD=EC,
由题意得,∠BDE=,∠BAC=41,
在Rt△ABC中,
BC=AC tan∠BAC=30×tan41≈26.1≈26,
在Rt△BDE中,
BE=DE tan∠BDE=30×tan19≈10.2,
∴AD=BC BE=26.1 10.2=15.9≈16.
答:居民楼的高度AD约为16米,建筑物的高度BC约为26米.
【点睛】考查直角三角形的边角关系,锐角三角函数,构造直角三角形利用锐角三角函数是解决问题的关键.
7.6
【分析】延长DA交CB的延长线于E,根据已知条件得到∠ABE=90°,根据邻补角的定义得到∠EAB=60°,得到∠E=30°,根据直角三角形的性质即可得到结论.
【详解】解:延长DA交CB的延长线于E,
∵∠ABC=90°,
∴∠ABE=90°,
∵∠DAB=120°,
∴∠EAB=60°,
∴∠E=30°,
∴AE=2AB=24,
∵∠D=90°,
∴∠C=60°,
∴DE= CD=30,
∴AD=DE-AE=6.
【点睛】本题考查了含30°角的直角三角形,正确的作出辅助线是解题的关键.
8.大楼CE的高度是26m.
【分析】作BF⊥AE于点F,根据三角函数的定义及解直角三角形的方法求出BF、CD即可.
【详解】解:作BF⊥AE于点F.则BF=DE.
在直角△ABF中,sin∠BAF=,则BF=AB sin∠BAF=10×=5(m).
在直角△CDB中,tan∠CBD=,则CD=BD tan65°=10×2.14=21.4(m).
则CE=DE+CD=BF+CD=5+21.4≈26(m).
答:大楼CE的高度是26m.
【点睛】此题主要考查解直角三角形,解题的关键是熟知三角函数的定义与性质.
9.(1)16cm
(2)105cm
【分析】(1)根据直角三角形中60°角解直角三角形即可;
(2)如图作DG⊥EF,,证明EF=EG+QC+CP,再分别运用解直角三角形求出EG、QC、CP即可.
【详解】(1)∵,,AB=32cm
∴(cm)
(2)如图,作DG⊥EF于点G,过点C作,交DG于点Q,交AB于点P,
∵DG⊥EF,AF⊥EF,
∴DG⊥PQ,AF⊥PQ,
∴四边形FPQG是矩形,FG=PQ,
∴(cm),(cm),
∵
∴∠EDG=75°-60°=15°
∴(cm)
∴EF=EG+FG=EG+PQ=EG+CQ+PC=(cm)
故E到地面的距离EF为105cm.
【点睛】本题主要考查解直角三角形,作辅助线构造相等线段,熟练运用解直角三角形求线段长度是解题关键.
答案第1页,共2页
答案第1页,共2页
