专题28.10解直角三角形 巩固篇 专项练习(含解析)2023-2024学年九年级数学下册人教版专项讲练
文档属性
| 名称 | 专题28.10解直角三角形 巩固篇 专项练习(含解析)2023-2024学年九年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 18:57:56 | ||
图片预览

文档简介
专题28.10解直角三角形(巩固篇)(专项练习)
一、单选题
1.已知△ABC 中, ∠C=90°,tanA= ,D 是 AC 上一点, ∠CBD=∠A, 则 cos∠CDB的值为( )
A. B. C. D.2
2.如图,将边长6cm的正方形纸片沿虚线剪开,剪成两个全等梯形.已知裁剪线与正方形的一边夹角为60°,则梯形纸片中较短的底边长为( )
A.(3﹣)cm B.(3﹣2)cm C.(6﹣)cm D.(6﹣2)cm
3.在平面直角坐标系中,直线与轴交于点,与轴交于点,将绕点逆时针旋转到如图的位置,的对应点恰好落在直线上,连接,则的长度为( )
A. B. C.2 D.
4.如图,在四边形ABCD中,∠DAB=∠B=60°,AD⊥CD,AC平分∠DAB,E为AB边的中点,连接DE交AC于F.若CD=1,则线段AF的长度为( )
A. B. C.1 D.
5.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB与CD相交于点P,则∠APD的余弦值为( )
A. B. C. D.
6.如图,在处测得点在北偏东方向上,在处测得点在北偏东方向上,若千米,则点两点的距离为()千米.
A.4 B. C.2 D.6
7.如图,在等腰中,于点,则的值( )
A. B. C. D.
8.如图,在矩形ABCD中,,,M是CD上的一点,将沿直线AM对折得到,若AN平分,则CN的长为( )
A. B. C. D.3
9.如图,无人机于空中处测得某建筑顶部处的仰角为,测得该建筑底部处的俯角为.若无人机的飞行高度为,则该建筑的高度为( ).(参考数据:,,)
A. B. C. D.
10.某同学利用数学知识测量建筑物DEFG的高度.他从点出发沿着坡度为的斜坡AB步行26米到达点B处,用测角仪测得建筑物顶端的仰角为37°,建筑物底端的俯角为30°,若AF为水平的地面,侧角仪竖直放置,其高度BC=1.6米,则此建筑物的高度DE约为(精确到米,参考数据:,)( )
A.米 B.米 C.米 D.米
二、填空题
11.如图,在△中,,D是边上的一点,,则AB .
12.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE垂直平分BO,交BD于点E,若AE,则矩形ABCD的周长为 .
13.如图,△ABC中,∠ABC=60°,∠ACB=45°,AC=2,则AB= .
14.如图,一艘船由A港沿北偏东方向航行至B港,然后再沿北偏西方向航行至C港,C港在A港北偏东方向,则A,C两港之间的距离为 .
15.如图,等腰直角△ABC的面积为16,点D在斜边AC的延长线上,∠BDC=30°,则△BDC的面积是 .
16.如图所示,在平面直角坐标系中,,,则点的坐标是 .
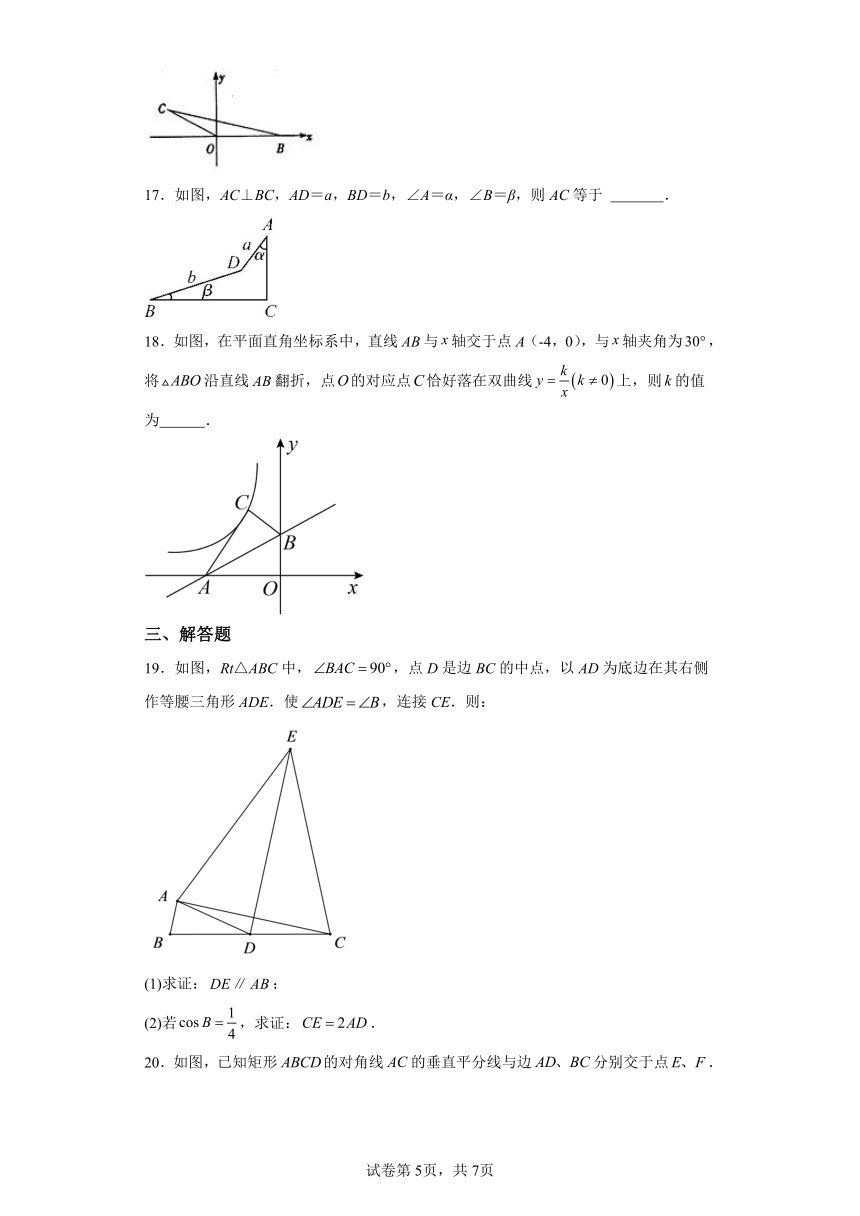
17.如图,AC⊥BC,AD=a,BD=b,∠A=α,∠B=β,则AC等于 .
18.如图,在平面直角坐标系中,直线与轴交于点A(-4,0),与轴夹角为,将沿直线翻折,点的对应点恰好落在双曲线上,则的值为 .
三、解答题
19.如图,Rt△ABC中,,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE.使,连接CE.则:
(1)求证:;
(2)若,求证:.
20.如图,已知矩形的对角线的垂直平分线与边分别交于点.
(1)求证:四边形是菱形.
(2)若,,则______.
21.如图,在三角形ABC中,∠ACB=90°,AB=5,AC=4,点D、点E分别为线段AC、AB上的点,连结DE.将△ADE沿DE折叠,使点A落在BC的延长线上的点F处,此时恰好有∠BFE=30°,则CF的长度为_____.
22.如图,在港口处的正东方向有两个相距的观测点,,一艘轮船从处出发沿东偏北方向航行至处,在,处分别测得,,求轮船航行的路程.(参考数据:,,,,结果保留整数)
23.如图,一艘渔船位于小岛B的北偏东30°方向,距离小岛40nmile的点A处.
(1)渔船航行多远距离小岛B最近(结果保留根号)?
(2)渔船到达距离小岛B最近点后,按原航向继续航行nmile到点C处时突然发生事故,问救援队从B处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少(结果保留根号)?
24.江阴芙蓉大道城市快速路在2020年5月份通车,在安装路灯过程中,工人师傅发现垂直于地面的灯柱OA与灯杆AB相交成一定的角度才能产生光照效果,路灯采用锥形灯罩,在地面上的照射区域OC长为8m,从O、C两处测得路灯B的仰角分别为∠BOC和∠BCO,且tan∠BOC=4,tan∠BCO=.
(1)求路灯B到地面的距离;
(2)若∠OAB=120°,求灯柱OA的高度(结果保留根号).
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】由已知条件,可得,设,由题意可得,即可算出,在中,根据勾股定理可得,由余弦定义进行计算即可得出答案.
【详解】解:,
,
设,
,
,
在中,
,
.
故选:B
【点睛】本题主要考查了解直角三角形,熟练掌握解直角三角形的方法进行求解是解决本题的关键.
2.A
【分析】过M点作ME⊥AD于E点,根据四边形ABCD是正方形,有AD=CD=6,∠C=∠D=90°,由裁剪的两个梯形全等,可得AN=MC;再证明四边形MCDE是矩形,即有MC=ED,ME=CD=6,进而有AN=ED,在Rt△MNE中,解直角三角形可得,则可得,问题得解.
【详解】如图,过M点作ME⊥AD于E点,
∵四边形ABCD是正方形,边长为6,
∴AD=CD=6,∠C=∠D=90°,
∵裁剪的两个梯形全等,
∴AN=MC,
∵ME⊥AD,
∴四边形MCDE是矩形,
∴MC=ED,ME=CD=6,
∴AN=ED,
根据题意有∠MNE=60°,
∴在Rt△MNE中,,
∴,
∴,
即梯形中较短的底为(cm),
故选:A.
【点睛】本题主要考查了正方形的、矩形的判定与性质、解直角三角形的应用等知识,根据梯形全等得出AN=MC是解答本题的关键.
3.B
【分析】先求出点A、B的坐标,可求得OA、OB,进而可求得∠OAB=60°,利用旋转的性质和等边三角形的判定与性质证明和为等边三角形得到即可求解.
【详解】解:对于,
当时,,当时,由得:,
则A(1,0),B(0,),
∴,,
∴,则∠OAB=60°,
由旋转性质得:,,,
∴是等边三角形,
∴,又
∴是等边三角形,
∴,
故选:B.
【点睛】本题考查一次函数图象与坐标轴的交点问题、旋转性质、等边三角形的判定与性质、解直角三角形,熟练掌握相关知识的联系与运用,证得是等边三角形是解答的关键.
4.D
【分析】延长AD、BC交于点G,将图形补充成等边三角形,利用△ACD和△ABC都是含30°角的直角三角形得出AC,AD,AB的长度,再利用直角三角形斜边上的中线等于斜边的一半得出EC的长度,用等边三角形的性质推导ECAD,继而得出△EFC∽△DFA,,最后结合CF=AC-AF利用这个比例式得到关于AF的方程,解出即可.
【详解】∵∠DAB=∠B=60°,AC平分∠DAB,
∴∠DAC=∠CAB=30°,
∵AD⊥CD,CD=1,
∴AD=,AC=2,
延长AD、BC交于点G,如图,
∵∠DAB=∠B=60°,
∴∠G=60°,
∴△ABG为等边三角形,
∵AC平分∠DAB,
∴C为GB的中点,且AC⊥GB,
∴AB=,
连接EC,
∵E为AB边的中点,AC⊥GB
∴EC=AB=,
∵C为GB的中点,
∴ECAD,
∴△EFC∽△DFA,
∴,即
∴
∴AF=.
故选:D.
【点睛】本题考查了等边三角形的判定与性质,含30°角的直角三角形的性质,相似三角形的判定与性质,利用判定△EFC∽△DFA并用其列出关于AF的方程是解题的关键.
5.C
【分析】取格点E,连接AE、BE,利用勾股定理的逆定理可证得△ABE是直角三角形,利用三角形外角的性质可得∠APD=∠ABE,在Rt△ABE中可求cos∠ABE,从而结论可得.
【详解】解:取格点E,连接AE、BE,如图:
设网格中的小正方形的边长为1,
则BE=,
AE=,
AB=.
∵BE2+AE2=2+8=10,
AB2=10,
∴BE2+AE2=AB2.
∴∠AEB=90°.
由题意:∠EBD=∠CDB=45°.
∵∠APD=∠CDB+∠PBD=45°+∠PBD,
∠ABE=∠DBE+∠PBD=45°+∠PBD,
∴∠APD=∠ABE.
在Rt△ABE中,cos∠ABE=.
∴cos∠APD=.
故选:C.
【点睛】本题主要考查了解直角三角形,本题是网格问题,巧妙的构造直角三角形是解题的关键.
6.D
【分析】根据题意可知,,千米,则根据三角函数可求、,再根据,利用三角函数可求BC,则.
【详解】解:由题意可知,,,
∵,
∴,
,
∴,
∴,
故选:D.
【点睛】本题考查的是解直角三角形的应用,掌握锐角三角函数的定义,正确标注方向角是解题的关键.
7.D
【分析】先由,易得,由可得,进而用勾股定理分别将BD、BC长用AB表示出来,再根据即可求解.
【详解】解:∵,,
∴,
∴,
又∵,
∴,
在中,,
∴,
故选:D
【点睛】本题主要考查了解三角形,涉及了等腰三角形性质和勾股定理以及三角函数的定义.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
8.C
【分析】过点N作CD的垂线交于点E,根据对折和平分线可以得到,再利用三角函数可以求出,,最后利用勾股定理可以求出CN的长.
【详解】解:如图,过点N作CD的垂线交于点E
由折叠可知:
,,
∵AN平分
∴
∴
∵
∴,
∴
∴
∵,
∴
∴,
∴
∴在中,由勾股定理可得:
故选:C
【点睛】本题考查了折叠的性质、解直角三角形以及勾股定理,正确作出辅助线是解题关键.
9.C
【分析】由题意作AE⊥BC于E,根据正切的定义求出AE,根据等腰直角三角形的性质求出BE,结合图形计算即可.
【详解】解:作AE⊥BC于E,
则四边形ADCE为矩形,
∴EC=AD=62,
在Rt△AEC中,,
则,
在Rt△AEB中,∠BAE=45°,
∴BE=AE=200,
∴BC=200+62=262(m),
则该建筑的高度BC为262m.
故选:C.
【点睛】本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.
10.C
【分析】如图,设CB⊥AF于N,过点C作CM⊥DE于M,根据坡度及AB的长可求出BN的长,进而可求出CN的长,即可得出ME的长,利用∠MBE的正切可求出CM的长,利用∠DCM的正切可求出DM的长,根据DE=DM+ME即可得答案.
【详解】如图,设CB⊥AF于N,过点C作CM⊥DE于M,
∵沿着坡度为的斜坡AB步行26米到达点B处,
∴,
∴AN=2.4BN,
∴BN2+(2.4BN)2=262,
解得:BN=10(负值舍去),
∴CN=BN+BC=11.6,
∴ME=11.6,
∵∠MCE=30°,
∴CM==11.6,
∵∠DCM=37°,
∴DM=CM·tan37°=8.7,
∴DE=ME+DM=11.6+8.7≈26.7(米),
故选:C.
【点睛】本题考查解直角三角形的应用,正确构造直角三角形并熟练掌握三角函数的定义及特殊角的三角函数值是解题关键.
11.##
【分析】如图,过点作,利用共用直角边列方程求出,再利用三角函数求出即可.
【详解】解:如图,过点作,设的长为
则: ,,
∴,
整理得:,解得: 或(舍),
又∵
∴ ,
故答案为: .
【点睛】本题考查解直角三角形.解题的关键是添加辅助线构造直角三角形,利用公共直角边别方程进行求解.
12.##
【分析】根据矩形的性质和线段垂直平分线的性质可证明△ABO是等边三角形,解直角三角形求出AB、AD即可求解.
【详解】解:∵四边形ABCD是矩形,
∴AO=OC=BO=OD,∠BAD=90°,
∵AE垂直平分BO,
∴AO=AB,∠AEB=90°,
∴AO=AB=BO,
∴△ABO是等边三角形,
∴∠ABO=60°,
在Rt△ABE中,AE,
∴,
在Rt△ABD中,AD=AB·tan60°=,
∴矩形ABCD的周长为2(AB+AD)=,
故答案为:.
【点睛】本题考查矩形的性质、线段垂直平分线 的性质、等边三角形的判定与性质、解直角三角形,熟练掌握矩形的性质和线段垂直平分线的性质,证得△ABO是等边三角形是解答的关键.
13.4
【分析】过点A作AD⊥BC于点D,得到一个30°和一个45°的直角三角形,再利用锐角三角形函数求解即可.
【详解】解:过点A作AD⊥BC于点D
∴∠ADC=∠ADB=90°
∵AC=2,∠ACB=45°
∴sin∠ACB==
∴AD=2
∵∠ABC=60°
∴sin∠ABC==
∴AB=4
故答案为:4.
【点睛】本题考查解直角三角形,锐角三角函数,利用特殊角60°和45°构造直角三角形是解决问题的关键.
14.
【分析】根据题意得,,,,过作于,解直角三角形即可得到结论.
【详解】解:根据题意得,,,,
过作于,
,
在中,,,
,
在中,,
,
,
,两港之间的距离为,
故答案为:.
【点睛】本题考查了解直角三角形的应用,方向角问题,三角形的内角和,是基础知识比较简单.
15.
【分析】作BH⊥AC于H.想办法求出AD.BH即可解决问题.
【详解】解:如图,作BH⊥AC于H.
∵等腰直角△ABC的面积为16,
∴BA=BC=,
∵BA=BC=,∠ABC=90°,BH⊥AC,
,
在Rt△BDH中,
∵∠BHD=90°,∠BDC =30°,
,
,
.
【点睛】本题考查等腰直角三角形的性质,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
16.
【分析】可过C点作CA⊥x轴于点A,由题可知∠COA=30°,再运用三角函数即可求解C点坐标.
【详解】解:过C点作CA⊥x轴于点A,
由题可知,∠COA=180°-150°=30°,
则AC=sin30°×OC=,AO= cos30°×OC=,
则C点坐标为:,
故答案为.
【点睛】本题考查了特殊角的三角函数,熟记几个特殊角的三角函数值是解题关键.
17.acosα+bsinβ
【分析】过点D作DE⊥AC于E,DF⊥BC于F,可得四边形DFCE是矩形,从而利用三角函数表示出AE,DF的长,即可求出AC的长.
【详解】解:过点D作DE⊥AC于E,DF⊥BC于F,
∵AC⊥BC,
∴四边形DFCE是矩形,
∴DF=CE,
∵AE=AD× cosα= acosα,
CE=DF=BD× sinβ= bsinβ,
∴AC=AE+EC= acosα+bsinβ.
故答案为acosα+bsinβ.
【点睛】本题考查了锐角三角函数的定义和矩形的性质和判定,熟练掌握相关定义和性质是解题的关键.
18.
【分析】设点的坐标为,过点作轴,作轴,根据折叠的性质可得,,,用锐角三角函数的定义求出,的长,则求出点的坐标,即可得出的值.
【详解】解:设点的坐标为,如图,过点作轴,作轴,
将沿直线翻折,
,,,
∴∠CAD=60°, ∠ACD=30°,
,
,
,
,
,
点在第二象限,
,
点恰好落在双曲线上,
.
故答案为:.
【点睛】本题主要考查了翻折的性质,锐角三角函数的知识,反比例函数的解析式的求法,理解翻折的性质,求出点的坐标是解答本题的关键.
19.(1)见解析
(2)见解析
【分析】(1)由直角三角形斜边中线的性质可知,即得出,再结合题意,即得出,从而证明;
(2)过点E作于点H,由,即得出,,从而得出,得出.根据平行线的性质得出,从而得出.又易证,得出,即可证明.
【详解】(1)∵,点D是边BC的中点,
∴,
∴.
∵,
∴,
∴;
(2)如图,过点E作于点H,
∵,
∴,
∵,
∴,
∴.
∵,
∴,
∴.
又∵,DE=DE,
∴,
∴,
∴,即.
【点睛】本题考查直角三角形斜边中线的性质,等腰三角形的判定和性质,平行线的判定和性质,解直角三角形以及全等三角形的判定和性质.正确作出辅助线是解题关键.
20.(1)见解析
(2)
【分析】(1)证明四边形是平行四边形,进而证明是菱形即可;
(2)根据三角函数和勾股定理解答即可.
【详解】(1)证明:在矩形中,,
∴,,
又∵,
∴≌,
∴,
∴四边形是平行四边形,
∵
∴平行四边形是菱形.
(2)∵,,∠B=90°,
∴,
∴,
∴,
∵四边形是菱形,
∴,,
∴,
∴,
故答案为:.
【点睛】本题考查了矩形的性质,菱形的判定与性质以及解三角形的知识,关键是掌握菱形的判定和性质.
21.
【分析】过点作于,根据勾股定理求得的长,继而求得,设,则,则,根据,解得,在中,,根据即可求解.
【详解】过点作于,如图,
∠BFE=30°,
,
∠ACB=90°,AB=5,AC=4,
,
,
,
,
,
,
设,则,,
,
解得,
,,
,
在中,,
,
故答案为:.
【点睛】本题考查了折叠的性质,解直角三角形,含30度角的直角三角形的性质,勾股定理,求得的长是解题的关键.
22..
【分析】过点作于点,根据锐角三角函数即可求出轮船航行的距离.
【详解】解:如图,过点作于点,
在中,,
,
,
在中,,
∴,
,
,
,
解得,
在中,,
,
即.
答:轮船航行的路程约为.
【点睛】本题考查了解直角三角形的应用方向角问题,锐角三角函数的应用,熟悉相关性质是解题的关键.
23.(1)渔船航行nmile距离小岛B最近;
(2)援队从B处出发沿点B的南偏东45°的方向航行到达事故地点航程最短,最短航程是nmile.
【分析】(1)过B作BM⊥AC于M,解直角三角形即可得到结论;
(2)在Rt△BCM中,解直角三角形求得∠MBC=60°,即可求得∠CBG=45°,nmile,可得到结论.
【详解】(1)解:过B作BM⊥AC于M,
由题意可知:∠BAM=45°,则∠ABM=45°,
在Rt△ABM中,
∵∠BAM=45°,
∴,
∴渔船航行nmile距离小岛B最近;
(2)解:∵nmile,
∴
∴∠MBC=60°,
∴∠CBG=180°﹣60°﹣45°﹣30°=45°,
在Rt△BCM中,
∵∠MBC=60°,
∴nmile.
故救援队从B处出发沿点B的南偏东45°的方向航行到达事故地点航程最短,最短航程是nmile.
【点睛】本题考查解非直角三角形,解题的关键是构造直角三角形,掌握解直角三角形的知识点.
24.(1)路灯B到地面的距离8m;(2)灯柱OA的高度为(8﹣)m.
【分析】(1)过点B作BF⊥OC于F,设BF=x.解直角三角形求得OF=x,CF=x,由OC=8求得x=8,据此知BF=8m;
(2)再过点A作AG⊥BF于点G,求得∠BAG=∠OAB﹣∠OAG=30°.解直角三角形可得BG,进而即可求得OA.
【详解】解:(1)过点B作BF⊥OC于F,设BF=x.
在Rt△BOF中,∵tan∠BOC==4,
∴OF=x,
在Rt△BCF中,∵tan∠BCO=,
∴CF=x,
∵OC=8,
∴x+x=8,
∴x=8,
∴BF=8m,
即路灯B到地面的距离8m;
(2)过点A作AG⊥BF于点G,可知四边形AGFO是矩形,
∵∠OAB=120°,
∴∠BAG=∠OAB﹣∠OAG=120°﹣90°=30°.
∵OF=×8=2,
∴AG=OF=2,
在Rt△BAG中,∵tan∠BAG=,
∴BG=tan30°×2=
∴OA=GF=(8﹣)(m),
即灯柱OA的高度为(8﹣)m.
【点睛】本题主要考查解直角三角形仰角俯角问题,解题的关键是结合题意构建直角三角形并熟练掌握三角函数的定义及其应用能力.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知△ABC 中, ∠C=90°,tanA= ,D 是 AC 上一点, ∠CBD=∠A, 则 cos∠CDB的值为( )
A. B. C. D.2
2.如图,将边长6cm的正方形纸片沿虚线剪开,剪成两个全等梯形.已知裁剪线与正方形的一边夹角为60°,则梯形纸片中较短的底边长为( )
A.(3﹣)cm B.(3﹣2)cm C.(6﹣)cm D.(6﹣2)cm
3.在平面直角坐标系中,直线与轴交于点,与轴交于点,将绕点逆时针旋转到如图的位置,的对应点恰好落在直线上,连接,则的长度为( )
A. B. C.2 D.
4.如图,在四边形ABCD中,∠DAB=∠B=60°,AD⊥CD,AC平分∠DAB,E为AB边的中点,连接DE交AC于F.若CD=1,则线段AF的长度为( )
A. B. C.1 D.
5.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB与CD相交于点P,则∠APD的余弦值为( )
A. B. C. D.
6.如图,在处测得点在北偏东方向上,在处测得点在北偏东方向上,若千米,则点两点的距离为()千米.
A.4 B. C.2 D.6
7.如图,在等腰中,于点,则的值( )
A. B. C. D.
8.如图,在矩形ABCD中,,,M是CD上的一点,将沿直线AM对折得到,若AN平分,则CN的长为( )
A. B. C. D.3
9.如图,无人机于空中处测得某建筑顶部处的仰角为,测得该建筑底部处的俯角为.若无人机的飞行高度为,则该建筑的高度为( ).(参考数据:,,)
A. B. C. D.
10.某同学利用数学知识测量建筑物DEFG的高度.他从点出发沿着坡度为的斜坡AB步行26米到达点B处,用测角仪测得建筑物顶端的仰角为37°,建筑物底端的俯角为30°,若AF为水平的地面,侧角仪竖直放置,其高度BC=1.6米,则此建筑物的高度DE约为(精确到米,参考数据:,)( )
A.米 B.米 C.米 D.米
二、填空题
11.如图,在△中,,D是边上的一点,,则AB .
12.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE垂直平分BO,交BD于点E,若AE,则矩形ABCD的周长为 .
13.如图,△ABC中,∠ABC=60°,∠ACB=45°,AC=2,则AB= .
14.如图,一艘船由A港沿北偏东方向航行至B港,然后再沿北偏西方向航行至C港,C港在A港北偏东方向,则A,C两港之间的距离为 .
15.如图,等腰直角△ABC的面积为16,点D在斜边AC的延长线上,∠BDC=30°,则△BDC的面积是 .
16.如图所示,在平面直角坐标系中,,,则点的坐标是 .
17.如图,AC⊥BC,AD=a,BD=b,∠A=α,∠B=β,则AC等于 .
18.如图,在平面直角坐标系中,直线与轴交于点A(-4,0),与轴夹角为,将沿直线翻折,点的对应点恰好落在双曲线上,则的值为 .
三、解答题
19.如图,Rt△ABC中,,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE.使,连接CE.则:
(1)求证:;
(2)若,求证:.
20.如图,已知矩形的对角线的垂直平分线与边分别交于点.
(1)求证:四边形是菱形.
(2)若,,则______.
21.如图,在三角形ABC中,∠ACB=90°,AB=5,AC=4,点D、点E分别为线段AC、AB上的点,连结DE.将△ADE沿DE折叠,使点A落在BC的延长线上的点F处,此时恰好有∠BFE=30°,则CF的长度为_____.
22.如图,在港口处的正东方向有两个相距的观测点,,一艘轮船从处出发沿东偏北方向航行至处,在,处分别测得,,求轮船航行的路程.(参考数据:,,,,结果保留整数)
23.如图,一艘渔船位于小岛B的北偏东30°方向,距离小岛40nmile的点A处.
(1)渔船航行多远距离小岛B最近(结果保留根号)?
(2)渔船到达距离小岛B最近点后,按原航向继续航行nmile到点C处时突然发生事故,问救援队从B处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少(结果保留根号)?
24.江阴芙蓉大道城市快速路在2020年5月份通车,在安装路灯过程中,工人师傅发现垂直于地面的灯柱OA与灯杆AB相交成一定的角度才能产生光照效果,路灯采用锥形灯罩,在地面上的照射区域OC长为8m,从O、C两处测得路灯B的仰角分别为∠BOC和∠BCO,且tan∠BOC=4,tan∠BCO=.
(1)求路灯B到地面的距离;
(2)若∠OAB=120°,求灯柱OA的高度(结果保留根号).
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】由已知条件,可得,设,由题意可得,即可算出,在中,根据勾股定理可得,由余弦定义进行计算即可得出答案.
【详解】解:,
,
设,
,
,
在中,
,
.
故选:B
【点睛】本题主要考查了解直角三角形,熟练掌握解直角三角形的方法进行求解是解决本题的关键.
2.A
【分析】过M点作ME⊥AD于E点,根据四边形ABCD是正方形,有AD=CD=6,∠C=∠D=90°,由裁剪的两个梯形全等,可得AN=MC;再证明四边形MCDE是矩形,即有MC=ED,ME=CD=6,进而有AN=ED,在Rt△MNE中,解直角三角形可得,则可得,问题得解.
【详解】如图,过M点作ME⊥AD于E点,
∵四边形ABCD是正方形,边长为6,
∴AD=CD=6,∠C=∠D=90°,
∵裁剪的两个梯形全等,
∴AN=MC,
∵ME⊥AD,
∴四边形MCDE是矩形,
∴MC=ED,ME=CD=6,
∴AN=ED,
根据题意有∠MNE=60°,
∴在Rt△MNE中,,
∴,
∴,
即梯形中较短的底为(cm),
故选:A.
【点睛】本题主要考查了正方形的、矩形的判定与性质、解直角三角形的应用等知识,根据梯形全等得出AN=MC是解答本题的关键.
3.B
【分析】先求出点A、B的坐标,可求得OA、OB,进而可求得∠OAB=60°,利用旋转的性质和等边三角形的判定与性质证明和为等边三角形得到即可求解.
【详解】解:对于,
当时,,当时,由得:,
则A(1,0),B(0,),
∴,,
∴,则∠OAB=60°,
由旋转性质得:,,,
∴是等边三角形,
∴,又
∴是等边三角形,
∴,
故选:B.
【点睛】本题考查一次函数图象与坐标轴的交点问题、旋转性质、等边三角形的判定与性质、解直角三角形,熟练掌握相关知识的联系与运用,证得是等边三角形是解答的关键.
4.D
【分析】延长AD、BC交于点G,将图形补充成等边三角形,利用△ACD和△ABC都是含30°角的直角三角形得出AC,AD,AB的长度,再利用直角三角形斜边上的中线等于斜边的一半得出EC的长度,用等边三角形的性质推导ECAD,继而得出△EFC∽△DFA,,最后结合CF=AC-AF利用这个比例式得到关于AF的方程,解出即可.
【详解】∵∠DAB=∠B=60°,AC平分∠DAB,
∴∠DAC=∠CAB=30°,
∵AD⊥CD,CD=1,
∴AD=,AC=2,
延长AD、BC交于点G,如图,
∵∠DAB=∠B=60°,
∴∠G=60°,
∴△ABG为等边三角形,
∵AC平分∠DAB,
∴C为GB的中点,且AC⊥GB,
∴AB=,
连接EC,
∵E为AB边的中点,AC⊥GB
∴EC=AB=,
∵C为GB的中点,
∴ECAD,
∴△EFC∽△DFA,
∴,即
∴
∴AF=.
故选:D.
【点睛】本题考查了等边三角形的判定与性质,含30°角的直角三角形的性质,相似三角形的判定与性质,利用判定△EFC∽△DFA并用其列出关于AF的方程是解题的关键.
5.C
【分析】取格点E,连接AE、BE,利用勾股定理的逆定理可证得△ABE是直角三角形,利用三角形外角的性质可得∠APD=∠ABE,在Rt△ABE中可求cos∠ABE,从而结论可得.
【详解】解:取格点E,连接AE、BE,如图:
设网格中的小正方形的边长为1,
则BE=,
AE=,
AB=.
∵BE2+AE2=2+8=10,
AB2=10,
∴BE2+AE2=AB2.
∴∠AEB=90°.
由题意:∠EBD=∠CDB=45°.
∵∠APD=∠CDB+∠PBD=45°+∠PBD,
∠ABE=∠DBE+∠PBD=45°+∠PBD,
∴∠APD=∠ABE.
在Rt△ABE中,cos∠ABE=.
∴cos∠APD=.
故选:C.
【点睛】本题主要考查了解直角三角形,本题是网格问题,巧妙的构造直角三角形是解题的关键.
6.D
【分析】根据题意可知,,千米,则根据三角函数可求、,再根据,利用三角函数可求BC,则.
【详解】解:由题意可知,,,
∵,
∴,
,
∴,
∴,
故选:D.
【点睛】本题考查的是解直角三角形的应用,掌握锐角三角函数的定义,正确标注方向角是解题的关键.
7.D
【分析】先由,易得,由可得,进而用勾股定理分别将BD、BC长用AB表示出来,再根据即可求解.
【详解】解:∵,,
∴,
∴,
又∵,
∴,
在中,,
∴,
故选:D
【点睛】本题主要考查了解三角形,涉及了等腰三角形性质和勾股定理以及三角函数的定义.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
8.C
【分析】过点N作CD的垂线交于点E,根据对折和平分线可以得到,再利用三角函数可以求出,,最后利用勾股定理可以求出CN的长.
【详解】解:如图,过点N作CD的垂线交于点E
由折叠可知:
,,
∵AN平分
∴
∴
∵
∴,
∴
∴
∵,
∴
∴,
∴
∴在中,由勾股定理可得:
故选:C
【点睛】本题考查了折叠的性质、解直角三角形以及勾股定理,正确作出辅助线是解题关键.
9.C
【分析】由题意作AE⊥BC于E,根据正切的定义求出AE,根据等腰直角三角形的性质求出BE,结合图形计算即可.
【详解】解:作AE⊥BC于E,
则四边形ADCE为矩形,
∴EC=AD=62,
在Rt△AEC中,,
则,
在Rt△AEB中,∠BAE=45°,
∴BE=AE=200,
∴BC=200+62=262(m),
则该建筑的高度BC为262m.
故选:C.
【点睛】本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.
10.C
【分析】如图,设CB⊥AF于N,过点C作CM⊥DE于M,根据坡度及AB的长可求出BN的长,进而可求出CN的长,即可得出ME的长,利用∠MBE的正切可求出CM的长,利用∠DCM的正切可求出DM的长,根据DE=DM+ME即可得答案.
【详解】如图,设CB⊥AF于N,过点C作CM⊥DE于M,
∵沿着坡度为的斜坡AB步行26米到达点B处,
∴,
∴AN=2.4BN,
∴BN2+(2.4BN)2=262,
解得:BN=10(负值舍去),
∴CN=BN+BC=11.6,
∴ME=11.6,
∵∠MCE=30°,
∴CM==11.6,
∵∠DCM=37°,
∴DM=CM·tan37°=8.7,
∴DE=ME+DM=11.6+8.7≈26.7(米),
故选:C.
【点睛】本题考查解直角三角形的应用,正确构造直角三角形并熟练掌握三角函数的定义及特殊角的三角函数值是解题关键.
11.##
【分析】如图,过点作,利用共用直角边列方程求出,再利用三角函数求出即可.
【详解】解:如图,过点作,设的长为
则: ,,
∴,
整理得:,解得: 或(舍),
又∵
∴ ,
故答案为: .
【点睛】本题考查解直角三角形.解题的关键是添加辅助线构造直角三角形,利用公共直角边别方程进行求解.
12.##
【分析】根据矩形的性质和线段垂直平分线的性质可证明△ABO是等边三角形,解直角三角形求出AB、AD即可求解.
【详解】解:∵四边形ABCD是矩形,
∴AO=OC=BO=OD,∠BAD=90°,
∵AE垂直平分BO,
∴AO=AB,∠AEB=90°,
∴AO=AB=BO,
∴△ABO是等边三角形,
∴∠ABO=60°,
在Rt△ABE中,AE,
∴,
在Rt△ABD中,AD=AB·tan60°=,
∴矩形ABCD的周长为2(AB+AD)=,
故答案为:.
【点睛】本题考查矩形的性质、线段垂直平分线 的性质、等边三角形的判定与性质、解直角三角形,熟练掌握矩形的性质和线段垂直平分线的性质,证得△ABO是等边三角形是解答的关键.
13.4
【分析】过点A作AD⊥BC于点D,得到一个30°和一个45°的直角三角形,再利用锐角三角形函数求解即可.
【详解】解:过点A作AD⊥BC于点D
∴∠ADC=∠ADB=90°
∵AC=2,∠ACB=45°
∴sin∠ACB==
∴AD=2
∵∠ABC=60°
∴sin∠ABC==
∴AB=4
故答案为:4.
【点睛】本题考查解直角三角形,锐角三角函数,利用特殊角60°和45°构造直角三角形是解决问题的关键.
14.
【分析】根据题意得,,,,过作于,解直角三角形即可得到结论.
【详解】解:根据题意得,,,,
过作于,
,
在中,,,
,
在中,,
,
,
,两港之间的距离为,
故答案为:.
【点睛】本题考查了解直角三角形的应用,方向角问题,三角形的内角和,是基础知识比较简单.
15.
【分析】作BH⊥AC于H.想办法求出AD.BH即可解决问题.
【详解】解:如图,作BH⊥AC于H.
∵等腰直角△ABC的面积为16,
∴BA=BC=,
∵BA=BC=,∠ABC=90°,BH⊥AC,
,
在Rt△BDH中,
∵∠BHD=90°,∠BDC =30°,
,
,
.
【点睛】本题考查等腰直角三角形的性质,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
16.
【分析】可过C点作CA⊥x轴于点A,由题可知∠COA=30°,再运用三角函数即可求解C点坐标.
【详解】解:过C点作CA⊥x轴于点A,
由题可知,∠COA=180°-150°=30°,
则AC=sin30°×OC=,AO= cos30°×OC=,
则C点坐标为:,
故答案为.
【点睛】本题考查了特殊角的三角函数,熟记几个特殊角的三角函数值是解题关键.
17.acosα+bsinβ
【分析】过点D作DE⊥AC于E,DF⊥BC于F,可得四边形DFCE是矩形,从而利用三角函数表示出AE,DF的长,即可求出AC的长.
【详解】解:过点D作DE⊥AC于E,DF⊥BC于F,
∵AC⊥BC,
∴四边形DFCE是矩形,
∴DF=CE,
∵AE=AD× cosα= acosα,
CE=DF=BD× sinβ= bsinβ,
∴AC=AE+EC= acosα+bsinβ.
故答案为acosα+bsinβ.
【点睛】本题考查了锐角三角函数的定义和矩形的性质和判定,熟练掌握相关定义和性质是解题的关键.
18.
【分析】设点的坐标为,过点作轴,作轴,根据折叠的性质可得,,,用锐角三角函数的定义求出,的长,则求出点的坐标,即可得出的值.
【详解】解:设点的坐标为,如图,过点作轴,作轴,
将沿直线翻折,
,,,
∴∠CAD=60°, ∠ACD=30°,
,
,
,
,
,
点在第二象限,
,
点恰好落在双曲线上,
.
故答案为:.
【点睛】本题主要考查了翻折的性质,锐角三角函数的知识,反比例函数的解析式的求法,理解翻折的性质,求出点的坐标是解答本题的关键.
19.(1)见解析
(2)见解析
【分析】(1)由直角三角形斜边中线的性质可知,即得出,再结合题意,即得出,从而证明;
(2)过点E作于点H,由,即得出,,从而得出,得出.根据平行线的性质得出,从而得出.又易证,得出,即可证明.
【详解】(1)∵,点D是边BC的中点,
∴,
∴.
∵,
∴,
∴;
(2)如图,过点E作于点H,
∵,
∴,
∵,
∴,
∴.
∵,
∴,
∴.
又∵,DE=DE,
∴,
∴,
∴,即.
【点睛】本题考查直角三角形斜边中线的性质,等腰三角形的判定和性质,平行线的判定和性质,解直角三角形以及全等三角形的判定和性质.正确作出辅助线是解题关键.
20.(1)见解析
(2)
【分析】(1)证明四边形是平行四边形,进而证明是菱形即可;
(2)根据三角函数和勾股定理解答即可.
【详解】(1)证明:在矩形中,,
∴,,
又∵,
∴≌,
∴,
∴四边形是平行四边形,
∵
∴平行四边形是菱形.
(2)∵,,∠B=90°,
∴,
∴,
∴,
∵四边形是菱形,
∴,,
∴,
∴,
故答案为:.
【点睛】本题考查了矩形的性质,菱形的判定与性质以及解三角形的知识,关键是掌握菱形的判定和性质.
21.
【分析】过点作于,根据勾股定理求得的长,继而求得,设,则,则,根据,解得,在中,,根据即可求解.
【详解】过点作于,如图,
∠BFE=30°,
,
∠ACB=90°,AB=5,AC=4,
,
,
,
,
,
,
设,则,,
,
解得,
,,
,
在中,,
,
故答案为:.
【点睛】本题考查了折叠的性质,解直角三角形,含30度角的直角三角形的性质,勾股定理,求得的长是解题的关键.
22..
【分析】过点作于点,根据锐角三角函数即可求出轮船航行的距离.
【详解】解:如图,过点作于点,
在中,,
,
,
在中,,
∴,
,
,
,
解得,
在中,,
,
即.
答:轮船航行的路程约为.
【点睛】本题考查了解直角三角形的应用方向角问题,锐角三角函数的应用,熟悉相关性质是解题的关键.
23.(1)渔船航行nmile距离小岛B最近;
(2)援队从B处出发沿点B的南偏东45°的方向航行到达事故地点航程最短,最短航程是nmile.
【分析】(1)过B作BM⊥AC于M,解直角三角形即可得到结论;
(2)在Rt△BCM中,解直角三角形求得∠MBC=60°,即可求得∠CBG=45°,nmile,可得到结论.
【详解】(1)解:过B作BM⊥AC于M,
由题意可知:∠BAM=45°,则∠ABM=45°,
在Rt△ABM中,
∵∠BAM=45°,
∴,
∴渔船航行nmile距离小岛B最近;
(2)解:∵nmile,
∴
∴∠MBC=60°,
∴∠CBG=180°﹣60°﹣45°﹣30°=45°,
在Rt△BCM中,
∵∠MBC=60°,
∴nmile.
故救援队从B处出发沿点B的南偏东45°的方向航行到达事故地点航程最短,最短航程是nmile.
【点睛】本题考查解非直角三角形,解题的关键是构造直角三角形,掌握解直角三角形的知识点.
24.(1)路灯B到地面的距离8m;(2)灯柱OA的高度为(8﹣)m.
【分析】(1)过点B作BF⊥OC于F,设BF=x.解直角三角形求得OF=x,CF=x,由OC=8求得x=8,据此知BF=8m;
(2)再过点A作AG⊥BF于点G,求得∠BAG=∠OAB﹣∠OAG=30°.解直角三角形可得BG,进而即可求得OA.
【详解】解:(1)过点B作BF⊥OC于F,设BF=x.
在Rt△BOF中,∵tan∠BOC==4,
∴OF=x,
在Rt△BCF中,∵tan∠BCO=,
∴CF=x,
∵OC=8,
∴x+x=8,
∴x=8,
∴BF=8m,
即路灯B到地面的距离8m;
(2)过点A作AG⊥BF于点G,可知四边形AGFO是矩形,
∵∠OAB=120°,
∴∠BAG=∠OAB﹣∠OAG=120°﹣90°=30°.
∵OF=×8=2,
∴AG=OF=2,
在Rt△BAG中,∵tan∠BAG=,
∴BG=tan30°×2=
∴OA=GF=(8﹣)(m),
即灯柱OA的高度为(8﹣)m.
【点睛】本题主要考查解直角三角形仰角俯角问题,解题的关键是结合题意构建直角三角形并熟练掌握三角函数的定义及其应用能力.
答案第1页,共2页
答案第1页,共2页
