专题28.11解直角三角形的应用 知识讲解(含解析)2023-2024学年九年级数学下册人教版专项讲练
文档属性
| 名称 | 专题28.11解直角三角形的应用 知识讲解(含解析)2023-2024学年九年级数学下册人教版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 18:59:20 | ||
图片预览

文档简介
专题28.11 解直角三角形的应用(知识讲解)
【学习目标】
1.理解用三角函数解决实际问题的有关概念;
2.理解并解决实际问题中转化为三角函数模型解决实际问题.
【要点梳理】
解直角三角形的知识应用很广泛,关键是把实际问题转化为数学模型,善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.
解这类问题的一般过程是:
(1)弄清题中名词、术语的意义,如仰角、俯角、坡度、坡角、方向角等概念,然后根据题意画出几何图形,建立数学模型.
(2)将已知条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形的问题.
(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.
(4)得出数学问题的答案并检验答案是否符合实际意义,得出实际问题的解.
拓展:
在用直角三角形知识解决实际问题时,经常会用到以下概念:
(1)坡角:坡面与水平面的夹角叫做坡角,用字母表示.
坡度(坡比):坡面的铅直高度h和水平距离的比叫做坡度,用字母表示,则,如图,坡度通常写成的形式.
(2)仰角、俯角:视线与水平线所成的角中,视线中水平线上方的叫做仰角,在水平线下方的叫做俯角,如图.
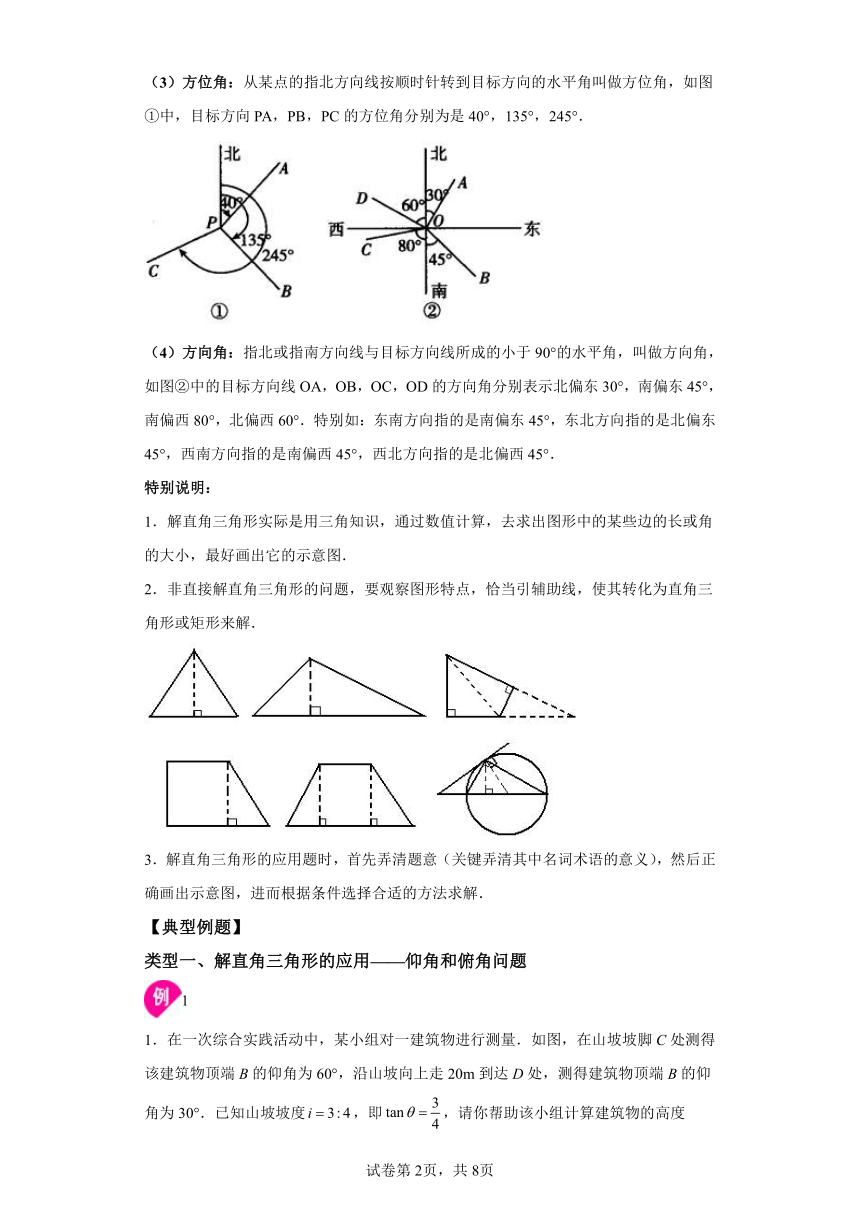
(3)方位角:从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角,如图①中,目标方向PA,PB,PC的方位角分别为是40°,135°,245°.
(4)方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角,如图②中的目标方向线OA,OB,OC,OD的方向角分别表示北偏东30°,南偏东45°,南偏西80°,北偏西60°.特别如:东南方向指的是南偏东45°,东北方向指的是北偏东45°,西南方向指的是南偏西45°,西北方向指的是北偏西45°.
特别说明:
1.解直角三角形实际是用三角知识,通过数值计算,去求出图形中的某些边的长或角的大小,最好画出它的示意图.
2.非直接解直角三角形的问题,要观察图形特点,恰当引辅助线,使其转化为直角三角形或矩形来解.
3.解直角三角形的应用题时,首先弄清题意(关键弄清其中名词术语的意义),然后正确画出示意图,进而根据条件选择合适的方法求解.
【典型例题】
类型一、解直角三角形的应用——仰角和俯角问题
1
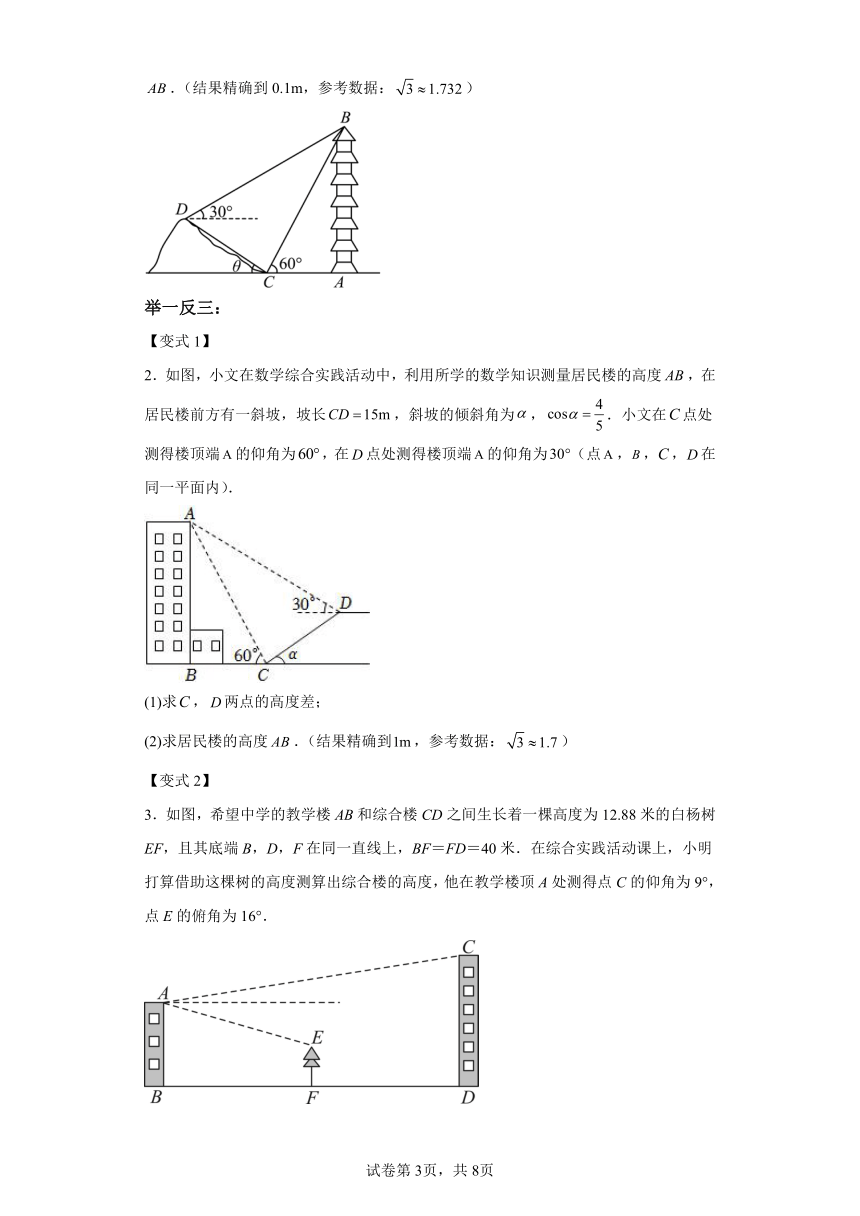
1.在一次综合实践活动中,某小组对一建筑物进行测量.如图,在山坡坡脚C处测得该建筑物顶端B的仰角为60°,沿山坡向上走20m到达D处,测得建筑物顶端B的仰角为30°.已知山坡坡度,即,请你帮助该小组计算建筑物的高度.(结果精确到0.1m,参考数据:)
举一反三:
【变式1】
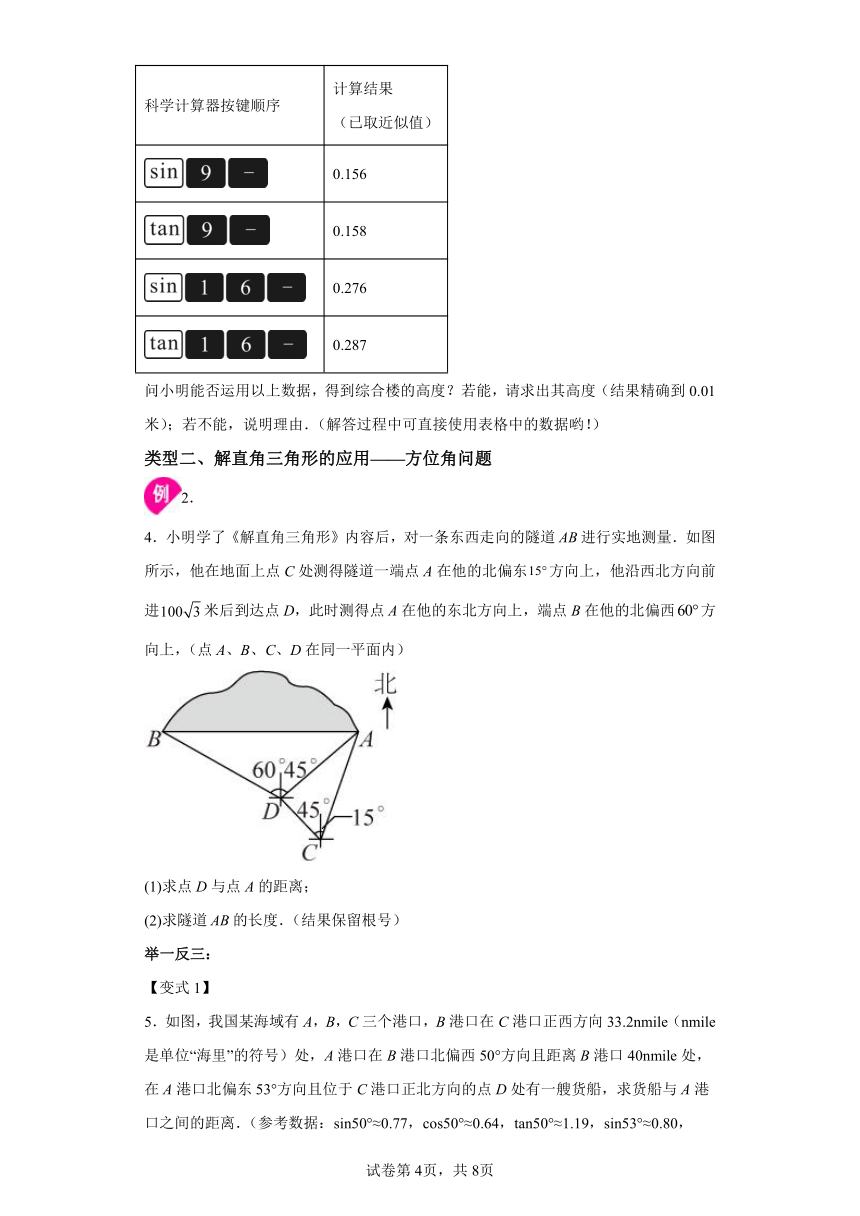
2.如图,小文在数学综合实践活动中,利用所学的数学知识测量居民楼的高度,在居民楼前方有一斜坡,坡长,斜坡的倾斜角为,.小文在点处测得楼顶端的仰角为,在点处测得楼顶端的仰角为(点,,,在同一平面内).
(1)求,两点的高度差;
(2)求居民楼的高度.(结果精确到,参考数据:)
【变式2】
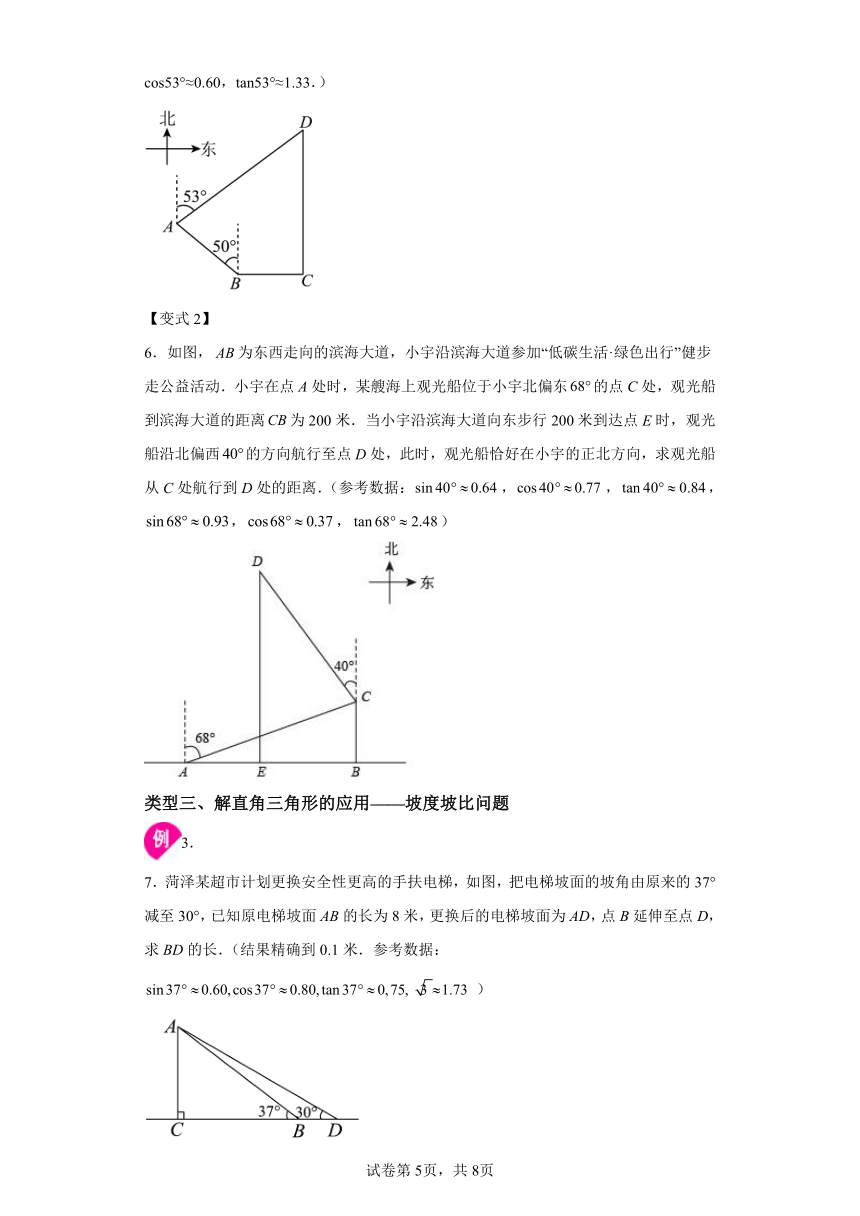
3.如图,希望中学的教学楼AB和综合楼CD之间生长着一棵高度为12.88米的白杨树EF,且其底端B,D,F在同一直线上,BF=FD=40米.在综合实践活动课上,小明打算借助这棵树的高度测算出综合楼的高度,他在教学楼顶A处测得点C的仰角为9°,点E的俯角为16°.
科学计算器按键顺序 计算结果 (已取近似值)
0.156
0.158
0.276
0.287
问小明能否运用以上数据,得到综合楼的高度?若能,请求出其高度(结果精确到0.01米);若不能,说明理由.(解答过程中可直接使用表格中的数据哟!)
类型二、解直角三角形的应用——方位角问题
2.
4.小明学了《解直角三角形》内容后,对一条东西走向的隧道进行实地测量.如图所示,他在地面上点C处测得隧道一端点A在他的北偏东方向上,他沿西北方向前进米后到达点D,此时测得点A在他的东北方向上,端点B在他的北偏西方向上,(点A、B、C、D在同一平面内)
(1)求点D与点A的距离;
(2)求隧道的长度.(结果保留根号)
举一反三:
【变式1】
5.如图,我国某海域有A,B,C三个港口,B港口在C港口正西方向33.2nmile(nmile是单位“海里”的符号)处,A港口在B港口北偏西50°方向且距离B港口40nmile处,在A港口北偏东53°方向且位于C港口正北方向的点D处有一艘货船,求货船与A港口之间的距离.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
【变式2】
6.如图,为东西走向的滨海大道,小宇沿滨海大道参加“低碳生活·绿色出行”健步走公益活动.小宇在点A处时,某艘海上观光船位于小宇北偏东的点C处,观光船到滨海大道的距离为200米.当小宇沿滨海大道向东步行200米到达点E时,观光船沿北偏西的方向航行至点D处,此时,观光船恰好在小宇的正北方向,求观光船从C处航行到D处的距离.(参考数据:,,,,,)
类型三、解直角三角形的应用——坡度坡比问题
3.
7.菏泽某超市计划更换安全性更高的手扶电梯,如图,把电梯坡面的坡角由原来的37°减至30°,已知原电梯坡面AB的长为8米,更换后的电梯坡面为AD,点B延伸至点D,求BD的长.(结果精确到0.1米.参考数据:)
举一反三:
【变式1】
8.如图是某水库大坝的横截面,坝高,背水坡BC的坡度为.为了对水库大坝进行升级加固,降低背水坡的倾斜程度,设计人员准备把背水坡的坡度改为,求背水坡新起点A与原起点B之间的距离.(参考数据:,.结果精确到0.1m)
【变式2】
9.宜宾东楼始建于唐代,重建于宜宾建城2200周年之际的2018年,新建成的东楼(如图1)成为长江首城会客厅、旅游休闲目的地、文化地标打卡地.某数学小组为测量东楼的高度,在梯步A处(如图2)测得楼顶D的仰角为45°,沿坡比为7:24的斜坡AB前行25米到达平台B处,测得楼顶D的仰角为60°,求东楼的高度DE.(结果精确到1米.参考数据:,)
类型四、解直角三角形的应用——其他问题
4.
10.2022年6月5日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,是垂直于工作台的移动基座,、为机械臂,m,m,m,.机械臂端点到工作台的距离m.
(1)求、两点之间的距离;
(2)求长.
(结果精确到0.1m,参考数据:,,,)
【变式1】
11.某型号飞机的机翼形状如图所示,根据图中数据计算的长度(结果保留小数点后一位,).
【变式2】
12.小强在物理课上学过平面镜成像知识后,在老师的带领下到某厂房做验证实验.如图,老师在该厂房顶部安装一平面镜MN,MN与墙面AB所成的角∠MNB=118°,厂房高AB= 8 m,房顶AM与水平地面平行,小强在点M的正下方C处从平面镜观察,能看到的水平地面上最远处D到他的距离CD是多少 (结果精确到0.1 m,参考数据:sin34°≈0.56, tan34°≈0.68,tan56°≈1.48)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.该建筑物的高度约为31.9m
【分析】如图,作交于点E,作交于点F,作交于点H,根据题意分别求出BF和AF的长,再根据即可求解.
【详解】作交于点E,作交于点F,作交于点H
则,,
∵
∴设,则
在中,
∴
∴
∴(负值舍去)
∴,
∴,
设,则
在中,
∵
∴
在中,
∵
∴
即
∵
∴
∴
∴
答:该建筑物的高度约为31.9m.
【点睛】本题考查解直角三角形的应用,熟练掌握坡角坡度,仰角的定义,添加合适的辅助线构造直角三角形是解题的关键.
2.(1)9m
(2)24m
【分析】(1)过点作,交的延长线于点,在中,可得,再利用勾股定理可求出,即可得出答案.
(2)过点作于,设,在中,,解得,在中,,,,求出的值,即可得出答案.
【详解】(1)解:过点作,交的延长线于点,
在中,,,
.
.
答:,两点的高度差为.
(2)过点作于,
由题意可得,,
设,
在中,,
解得,
在中,,,
,
解得,
.
答:居民楼的高度约为.
【点睛】本题考查解直角三角形的应用仰角俯角问题、坡度坡角问题,熟练掌握锐角三角函数的定义是解答本题的关键.
3.能,综合楼的高度约是37.00米.
【分析】在Rt△AEG中,利用正切函数求得AG的长,在Rt△ACH中,利用正切函数求得CH的长,据此求解即可得到综合楼的高度.
【详解】解:小明能运用以上数据,得到综合楼的高度,理由如下:
作EG⊥AB,垂足为G,作AH⊥CD,垂足为H,如图:
·
由题意知,EG= BF= 40米,EF= BG= 12.88米,∠HAE= 16°= ∠AEG= 16°,∠CAH =9°,
在Rt△AEG中,
tan ∠AEG=,
∴tan 16°=,即0.287≈,
∴AG = 40×0.287=11.48(米),
∴AB = AG+BG=11.48+12.88= 24.36(米),
∴HD= AB =24.36米,
在Rt△ACH中,AH =BD= BF+FD=80米,
tan∠CAH =,
∴tan 9°= ,即0.158≈,
∴CH =80×0.158= 12.64(米),
∴CD=CH+HD = 12.64+24.36= 37.00(米),
则综合楼的高度约是37.00米.
【点睛】本题考查了解直角三角形的应用-仰角俯角问题,解决本题的关键是掌握仰角和俯角定义.
4.(1)点D与点A的距离为300米
(2)隧道的长为米
【分析】(1)根据方位角图,易知,,解即可求解;
(2)过点D作于点E.分别解,求出和,即可求出隧道的长
【详解】(1)由题意可知:,
在中,
∴(米)
答:点D与点A的距离为300米.
(2)过点D作于点E.
∵是东西走向
∴
在中,
∴
在中,
∴
∴(米)
答:隧道的长为米
【点睛】本题考查的是解直角三角形的应用-方向角问题,掌握方向角的概念、熟记特殊角的三角函数值是解题的关键.
5.货船与A港口之间的距离约为80海里
【分析】过点A作AE⊥CD,垂足为E,过点B作BF⊥AE,垂足为F,根据题意得:EF=BC=33.2海里,AG∥DC,从而可得∠ADC=53°,然后在Rt△AEF中,利用锐角三角函数的定义求出AF的长,从而求出AE的长,最后在Rt△ADE中,利用锐角三角函数的定义求出AD的长,进行计算即可解答.
【详解】解:过点A作AE⊥CD,垂足为E,过点B作BF⊥AE,垂足为F,
由题意得:
EF=BC=33.2海里,AG∥DC,
∴∠GAD=∠ADC=53°,
在Rt△ABF中,∠ABF=50°,AB=40海里,
∴AF=AB sin50°≈40×0.77=30.8(海里),
∴AE=AF+EF=64(海里),
在Rt△ADE中,AD=≈=80(海里),
∴货船与A港口之间的距离约为80海里.
【点睛】本题考查了解直角三角形的应用-方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
6.观光船从C处航行到D处的距离为米
【分析】过点C作于点F,根据题意利用正切函数可得,由矩形的判定和性质得出,结合图形利用锐角三角函数解三角形即可.
【详解】解:过点C作于点F,
由题意得,,
在中,,
∵
∴
∴
∵
∴四边形为矩形
∴.
在中,
∵
∴
答:观光船从C处航行到D处的距离为米.
【点睛】题目主要考查解三角形的应用,理解题意,找准各角之间的关系,利用锐角三角函数解三角形是解题关键.
7.约为1.9米
【分析】根据正弦的定义求出AC,根据余弦的定义求出BC,根据正切的定义求出CD,结合图形计算,得到答案.
【详解】解:在Rt△ABC中,AB=8米,∠ABC=37°,
则AC=AB sin∠ABC≈8×0.60=4.8(米),
BC=AB cos∠ABC≈8×0.80=6.40(米),
在Rt△ADC中,∠ADC=30°,
则CD=≈8.30(米),
∴BD=CD-BC=8.30-6.40≈1.9(米),
答:BD的长约为1.9米.
【点睛】本题考查的是解直角三角形的应用—坡度坡角问题,掌握锐角三角函数的定义是解题的关键.
8.背水坡新起点A与原起点B之间的距离约为14.6m
【分析】通过解直角三角形和,分别求出AD和BD的长,由求出AB的长.
【详解】解:在中,∵背水坡BC的坡度,
∴,
∴.
在中,∵背水坡AC的坡度,
∴,
∴,
∴.
答:背水坡新起点A与原起点B之间的距离约为14.6m.
【点睛】本题考查了解直角三角形的应用,解答本题的关键是理解坡度、坡比的含义,构造直角三角形,利用三角函数表示相关线段的长度.
9.米
【分析】根据,米,设,则,根据勾股定理求得,又设米,则米,米,求出DE,根据列出方程,解方程进而根据即可求解.
【详解】解:在中,,米,
设,则,由,
得,
解得:,
∴米,米
又设米,则米,米
在中,,
则,
∴(米),
在中,,则,
∴,
∴,
解得:,
∴(米).
∴东楼的高度约为40米.
【点睛】本题考查了解直角三角形的实际应用,掌握三角形中的边角关系是解题的关键.
10.(1)6.7m
(2)4.5m
【分析】(1)连接,过点作,交的延长线于,根据锐角三角函数定义和勾股定理即可解决问题.
(2)过点作,垂足为,根据锐角三角函数定义和勾股定理即可解决问题.
【详解】(1)解:如图2,连接,过点作,交的延长线于.
在中,,
,所以,
,所以,
在中,m,m,
根据勾股定理得m,
答:、两点之间的距离约6.7m.
(2)如图2,过点作,垂足为,
则四边形为矩形,m,,
所以m,
在中,m,m,
根据勾股定理得m.
m.
答:的长为4.5m.
【点睛】求角的三角画数值或者求线段的长时,我们经常通过观察图形将所求的角成者线段转化到直角三角形中(如果没有直角三角形,设法构造直角三角形),再利用锐角三角画数求解
11.的长度约为10.2米
【分析】延长交的垂线于点,交于点,则四边形是矩形,根据图示,可得四边形是正方形,解,即可求解.
【详解】解:如图,延长交的垂线于点,交于点,则四边形是矩形,
,
四边形是正方形,
,
,,
,
中,,
,
中,,
(米).
【点睛】本题考查了解直角三角形的应用,掌握直角三角形中的边角关系是解题的关键.
12.
【分析】过M点作ME⊥MN交CD于E点,证明四边形ABCM为矩形得到CM=AB=8,∠NMC=180°-∠BNM=62°,利用物理学入射光线与反射光线之间的关系得到∠EMD=∠EMC,且∠CME=90°-∠CMN=28°,进而求出∠CMD=56°,最后在Rt△CMD中由tan∠CMD即可求解.
【详解】解:过M点作ME⊥MN交CD于E点,如下图所示:
∵C点在M点正下方,
∴CM⊥CD,即∠MCD=90°,
∵房顶AM与水平地面平行,AB为墙面,
∴四边形AMCB为矩形,
∴MC=AB=8m,AB∥CM,
∴∠NMC=180°-∠BNM=180°-118°=62°,
∵地面上的点D经过平面镜MN反射后落在点C,结合物理学知识可知:
∴∠NME=90°,
∴∠EMD=∠EMC=90°-∠NMC=90°-62°=28°,
∴∠CMD=56°,
在Rt△CMD中,,代入数据:,
∴,
即水平地面上最远处D到小强的距离CD是.
【点睛】本题借助平面镜入射光线与反射光线相关的物理学知识考查了解直角三角形,解题的关键是读懂题意,利用数形结合的思想解答.
答案第1页,共2页
答案第1页,共2页
【学习目标】
1.理解用三角函数解决实际问题的有关概念;
2.理解并解决实际问题中转化为三角函数模型解决实际问题.
【要点梳理】
解直角三角形的知识应用很广泛,关键是把实际问题转化为数学模型,善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.
解这类问题的一般过程是:
(1)弄清题中名词、术语的意义,如仰角、俯角、坡度、坡角、方向角等概念,然后根据题意画出几何图形,建立数学模型.
(2)将已知条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形的问题.
(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.
(4)得出数学问题的答案并检验答案是否符合实际意义,得出实际问题的解.
拓展:
在用直角三角形知识解决实际问题时,经常会用到以下概念:
(1)坡角:坡面与水平面的夹角叫做坡角,用字母表示.
坡度(坡比):坡面的铅直高度h和水平距离的比叫做坡度,用字母表示,则,如图,坡度通常写成的形式.
(2)仰角、俯角:视线与水平线所成的角中,视线中水平线上方的叫做仰角,在水平线下方的叫做俯角,如图.
(3)方位角:从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角,如图①中,目标方向PA,PB,PC的方位角分别为是40°,135°,245°.
(4)方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角,如图②中的目标方向线OA,OB,OC,OD的方向角分别表示北偏东30°,南偏东45°,南偏西80°,北偏西60°.特别如:东南方向指的是南偏东45°,东北方向指的是北偏东45°,西南方向指的是南偏西45°,西北方向指的是北偏西45°.
特别说明:
1.解直角三角形实际是用三角知识,通过数值计算,去求出图形中的某些边的长或角的大小,最好画出它的示意图.
2.非直接解直角三角形的问题,要观察图形特点,恰当引辅助线,使其转化为直角三角形或矩形来解.
3.解直角三角形的应用题时,首先弄清题意(关键弄清其中名词术语的意义),然后正确画出示意图,进而根据条件选择合适的方法求解.
【典型例题】
类型一、解直角三角形的应用——仰角和俯角问题
1
1.在一次综合实践活动中,某小组对一建筑物进行测量.如图,在山坡坡脚C处测得该建筑物顶端B的仰角为60°,沿山坡向上走20m到达D处,测得建筑物顶端B的仰角为30°.已知山坡坡度,即,请你帮助该小组计算建筑物的高度.(结果精确到0.1m,参考数据:)
举一反三:
【变式1】
2.如图,小文在数学综合实践活动中,利用所学的数学知识测量居民楼的高度,在居民楼前方有一斜坡,坡长,斜坡的倾斜角为,.小文在点处测得楼顶端的仰角为,在点处测得楼顶端的仰角为(点,,,在同一平面内).
(1)求,两点的高度差;
(2)求居民楼的高度.(结果精确到,参考数据:)
【变式2】
3.如图,希望中学的教学楼AB和综合楼CD之间生长着一棵高度为12.88米的白杨树EF,且其底端B,D,F在同一直线上,BF=FD=40米.在综合实践活动课上,小明打算借助这棵树的高度测算出综合楼的高度,他在教学楼顶A处测得点C的仰角为9°,点E的俯角为16°.
科学计算器按键顺序 计算结果 (已取近似值)
0.156
0.158
0.276
0.287
问小明能否运用以上数据,得到综合楼的高度?若能,请求出其高度(结果精确到0.01米);若不能,说明理由.(解答过程中可直接使用表格中的数据哟!)
类型二、解直角三角形的应用——方位角问题
2.
4.小明学了《解直角三角形》内容后,对一条东西走向的隧道进行实地测量.如图所示,他在地面上点C处测得隧道一端点A在他的北偏东方向上,他沿西北方向前进米后到达点D,此时测得点A在他的东北方向上,端点B在他的北偏西方向上,(点A、B、C、D在同一平面内)
(1)求点D与点A的距离;
(2)求隧道的长度.(结果保留根号)
举一反三:
【变式1】
5.如图,我国某海域有A,B,C三个港口,B港口在C港口正西方向33.2nmile(nmile是单位“海里”的符号)处,A港口在B港口北偏西50°方向且距离B港口40nmile处,在A港口北偏东53°方向且位于C港口正北方向的点D处有一艘货船,求货船与A港口之间的距离.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
【变式2】
6.如图,为东西走向的滨海大道,小宇沿滨海大道参加“低碳生活·绿色出行”健步走公益活动.小宇在点A处时,某艘海上观光船位于小宇北偏东的点C处,观光船到滨海大道的距离为200米.当小宇沿滨海大道向东步行200米到达点E时,观光船沿北偏西的方向航行至点D处,此时,观光船恰好在小宇的正北方向,求观光船从C处航行到D处的距离.(参考数据:,,,,,)
类型三、解直角三角形的应用——坡度坡比问题
3.
7.菏泽某超市计划更换安全性更高的手扶电梯,如图,把电梯坡面的坡角由原来的37°减至30°,已知原电梯坡面AB的长为8米,更换后的电梯坡面为AD,点B延伸至点D,求BD的长.(结果精确到0.1米.参考数据:)
举一反三:
【变式1】
8.如图是某水库大坝的横截面,坝高,背水坡BC的坡度为.为了对水库大坝进行升级加固,降低背水坡的倾斜程度,设计人员准备把背水坡的坡度改为,求背水坡新起点A与原起点B之间的距离.(参考数据:,.结果精确到0.1m)
【变式2】
9.宜宾东楼始建于唐代,重建于宜宾建城2200周年之际的2018年,新建成的东楼(如图1)成为长江首城会客厅、旅游休闲目的地、文化地标打卡地.某数学小组为测量东楼的高度,在梯步A处(如图2)测得楼顶D的仰角为45°,沿坡比为7:24的斜坡AB前行25米到达平台B处,测得楼顶D的仰角为60°,求东楼的高度DE.(结果精确到1米.参考数据:,)
类型四、解直角三角形的应用——其他问题
4.
10.2022年6月5日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,是垂直于工作台的移动基座,、为机械臂,m,m,m,.机械臂端点到工作台的距离m.
(1)求、两点之间的距离;
(2)求长.
(结果精确到0.1m,参考数据:,,,)
【变式1】
11.某型号飞机的机翼形状如图所示,根据图中数据计算的长度(结果保留小数点后一位,).
【变式2】
12.小强在物理课上学过平面镜成像知识后,在老师的带领下到某厂房做验证实验.如图,老师在该厂房顶部安装一平面镜MN,MN与墙面AB所成的角∠MNB=118°,厂房高AB= 8 m,房顶AM与水平地面平行,小强在点M的正下方C处从平面镜观察,能看到的水平地面上最远处D到他的距离CD是多少 (结果精确到0.1 m,参考数据:sin34°≈0.56, tan34°≈0.68,tan56°≈1.48)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.该建筑物的高度约为31.9m
【分析】如图,作交于点E,作交于点F,作交于点H,根据题意分别求出BF和AF的长,再根据即可求解.
【详解】作交于点E,作交于点F,作交于点H
则,,
∵
∴设,则
在中,
∴
∴
∴(负值舍去)
∴,
∴,
设,则
在中,
∵
∴
在中,
∵
∴
即
∵
∴
∴
∴
答:该建筑物的高度约为31.9m.
【点睛】本题考查解直角三角形的应用,熟练掌握坡角坡度,仰角的定义,添加合适的辅助线构造直角三角形是解题的关键.
2.(1)9m
(2)24m
【分析】(1)过点作,交的延长线于点,在中,可得,再利用勾股定理可求出,即可得出答案.
(2)过点作于,设,在中,,解得,在中,,,,求出的值,即可得出答案.
【详解】(1)解:过点作,交的延长线于点,
在中,,,
.
.
答:,两点的高度差为.
(2)过点作于,
由题意可得,,
设,
在中,,
解得,
在中,,,
,
解得,
.
答:居民楼的高度约为.
【点睛】本题考查解直角三角形的应用仰角俯角问题、坡度坡角问题,熟练掌握锐角三角函数的定义是解答本题的关键.
3.能,综合楼的高度约是37.00米.
【分析】在Rt△AEG中,利用正切函数求得AG的长,在Rt△ACH中,利用正切函数求得CH的长,据此求解即可得到综合楼的高度.
【详解】解:小明能运用以上数据,得到综合楼的高度,理由如下:
作EG⊥AB,垂足为G,作AH⊥CD,垂足为H,如图:
·
由题意知,EG= BF= 40米,EF= BG= 12.88米,∠HAE= 16°= ∠AEG= 16°,∠CAH =9°,
在Rt△AEG中,
tan ∠AEG=,
∴tan 16°=,即0.287≈,
∴AG = 40×0.287=11.48(米),
∴AB = AG+BG=11.48+12.88= 24.36(米),
∴HD= AB =24.36米,
在Rt△ACH中,AH =BD= BF+FD=80米,
tan∠CAH =,
∴tan 9°= ,即0.158≈,
∴CH =80×0.158= 12.64(米),
∴CD=CH+HD = 12.64+24.36= 37.00(米),
则综合楼的高度约是37.00米.
【点睛】本题考查了解直角三角形的应用-仰角俯角问题,解决本题的关键是掌握仰角和俯角定义.
4.(1)点D与点A的距离为300米
(2)隧道的长为米
【分析】(1)根据方位角图,易知,,解即可求解;
(2)过点D作于点E.分别解,求出和,即可求出隧道的长
【详解】(1)由题意可知:,
在中,
∴(米)
答:点D与点A的距离为300米.
(2)过点D作于点E.
∵是东西走向
∴
在中,
∴
在中,
∴
∴(米)
答:隧道的长为米
【点睛】本题考查的是解直角三角形的应用-方向角问题,掌握方向角的概念、熟记特殊角的三角函数值是解题的关键.
5.货船与A港口之间的距离约为80海里
【分析】过点A作AE⊥CD,垂足为E,过点B作BF⊥AE,垂足为F,根据题意得:EF=BC=33.2海里,AG∥DC,从而可得∠ADC=53°,然后在Rt△AEF中,利用锐角三角函数的定义求出AF的长,从而求出AE的长,最后在Rt△ADE中,利用锐角三角函数的定义求出AD的长,进行计算即可解答.
【详解】解:过点A作AE⊥CD,垂足为E,过点B作BF⊥AE,垂足为F,
由题意得:
EF=BC=33.2海里,AG∥DC,
∴∠GAD=∠ADC=53°,
在Rt△ABF中,∠ABF=50°,AB=40海里,
∴AF=AB sin50°≈40×0.77=30.8(海里),
∴AE=AF+EF=64(海里),
在Rt△ADE中,AD=≈=80(海里),
∴货船与A港口之间的距离约为80海里.
【点睛】本题考查了解直角三角形的应用-方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
6.观光船从C处航行到D处的距离为米
【分析】过点C作于点F,根据题意利用正切函数可得,由矩形的判定和性质得出,结合图形利用锐角三角函数解三角形即可.
【详解】解:过点C作于点F,
由题意得,,
在中,,
∵
∴
∴
∵
∴四边形为矩形
∴.
在中,
∵
∴
答:观光船从C处航行到D处的距离为米.
【点睛】题目主要考查解三角形的应用,理解题意,找准各角之间的关系,利用锐角三角函数解三角形是解题关键.
7.约为1.9米
【分析】根据正弦的定义求出AC,根据余弦的定义求出BC,根据正切的定义求出CD,结合图形计算,得到答案.
【详解】解:在Rt△ABC中,AB=8米,∠ABC=37°,
则AC=AB sin∠ABC≈8×0.60=4.8(米),
BC=AB cos∠ABC≈8×0.80=6.40(米),
在Rt△ADC中,∠ADC=30°,
则CD=≈8.30(米),
∴BD=CD-BC=8.30-6.40≈1.9(米),
答:BD的长约为1.9米.
【点睛】本题考查的是解直角三角形的应用—坡度坡角问题,掌握锐角三角函数的定义是解题的关键.
8.背水坡新起点A与原起点B之间的距离约为14.6m
【分析】通过解直角三角形和,分别求出AD和BD的长,由求出AB的长.
【详解】解:在中,∵背水坡BC的坡度,
∴,
∴.
在中,∵背水坡AC的坡度,
∴,
∴,
∴.
答:背水坡新起点A与原起点B之间的距离约为14.6m.
【点睛】本题考查了解直角三角形的应用,解答本题的关键是理解坡度、坡比的含义,构造直角三角形,利用三角函数表示相关线段的长度.
9.米
【分析】根据,米,设,则,根据勾股定理求得,又设米,则米,米,求出DE,根据列出方程,解方程进而根据即可求解.
【详解】解:在中,,米,
设,则,由,
得,
解得:,
∴米,米
又设米,则米,米
在中,,
则,
∴(米),
在中,,则,
∴,
∴,
解得:,
∴(米).
∴东楼的高度约为40米.
【点睛】本题考查了解直角三角形的实际应用,掌握三角形中的边角关系是解题的关键.
10.(1)6.7m
(2)4.5m
【分析】(1)连接,过点作,交的延长线于,根据锐角三角函数定义和勾股定理即可解决问题.
(2)过点作,垂足为,根据锐角三角函数定义和勾股定理即可解决问题.
【详解】(1)解:如图2,连接,过点作,交的延长线于.
在中,,
,所以,
,所以,
在中,m,m,
根据勾股定理得m,
答:、两点之间的距离约6.7m.
(2)如图2,过点作,垂足为,
则四边形为矩形,m,,
所以m,
在中,m,m,
根据勾股定理得m.
m.
答:的长为4.5m.
【点睛】求角的三角画数值或者求线段的长时,我们经常通过观察图形将所求的角成者线段转化到直角三角形中(如果没有直角三角形,设法构造直角三角形),再利用锐角三角画数求解
11.的长度约为10.2米
【分析】延长交的垂线于点,交于点,则四边形是矩形,根据图示,可得四边形是正方形,解,即可求解.
【详解】解:如图,延长交的垂线于点,交于点,则四边形是矩形,
,
四边形是正方形,
,
,,
,
中,,
,
中,,
(米).
【点睛】本题考查了解直角三角形的应用,掌握直角三角形中的边角关系是解题的关键.
12.
【分析】过M点作ME⊥MN交CD于E点,证明四边形ABCM为矩形得到CM=AB=8,∠NMC=180°-∠BNM=62°,利用物理学入射光线与反射光线之间的关系得到∠EMD=∠EMC,且∠CME=90°-∠CMN=28°,进而求出∠CMD=56°,最后在Rt△CMD中由tan∠CMD即可求解.
【详解】解:过M点作ME⊥MN交CD于E点,如下图所示:
∵C点在M点正下方,
∴CM⊥CD,即∠MCD=90°,
∵房顶AM与水平地面平行,AB为墙面,
∴四边形AMCB为矩形,
∴MC=AB=8m,AB∥CM,
∴∠NMC=180°-∠BNM=180°-118°=62°,
∵地面上的点D经过平面镜MN反射后落在点C,结合物理学知识可知:
∴∠NME=90°,
∴∠EMD=∠EMC=90°-∠NMC=90°-62°=28°,
∴∠CMD=56°,
在Rt△CMD中,,代入数据:,
∴,
即水平地面上最远处D到小强的距离CD是.
【点睛】本题借助平面镜入射光线与反射光线相关的物理学知识考查了解直角三角形,解题的关键是读懂题意,利用数形结合的思想解答.
答案第1页,共2页
答案第1页,共2页
