探索型问题(上海市闵行区)
图片预览





文档简介
课件21张PPT。专题突破2、探索性问题考点1、条件探索型解这类问题的一般思路是:从结论出发,执果寻因,
逆向推理,逐步探寻结论成立的充分条件,或把可能
产生结论的条件一一列出,逐个分析考察,答案不唯一例1、在梯形ABCD中,AB∥CD,E、F、G、H分别是
边AB,BC,CD,DA的中点,要使EFGH是菱形,则
下列补充条件中不正确的是( )
(A)AC⊥BD;(B)AC = BD;
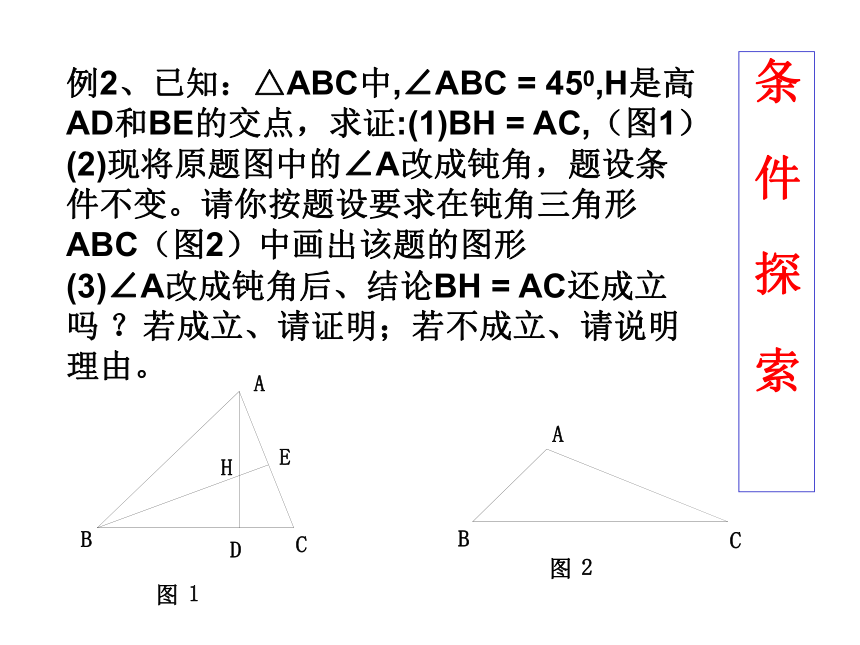
(C)AD = BC;(D)∠D = ∠C例2、已知:△ABC中,∠ABC = 450,H是高AD和BE的交点,求证:(1)BH = AC,(图1)条 件 探 索 (2)现将原题图中的∠A改成钝角,题设条件不变。请你按题设要求在钝角三角形ABC(图2)中画出该题的图形(3)∠A改成钝角后、结论BH = AC还成立吗 ?若成立、请证明;若不成立、请说明理由。
答:BH=AC还成立
证明:∵HD,CE是高,∴∠1=∠2=∠3=900
∴∠5+∠C=900 ,∠4+∠H=900
∵∠4=∠5,∴∠H=∠C
∵∠1=900,∠ABC=450,∴∠6=∠ABC=450
∴BD=AD
∴△HBD≌△CAD
∴BH=AC 考点2、结论探索型 猜想型,需探索的结论需要依据题设条件从简单
情况或特殊情况入手进行归纳,大胆猜想得出结
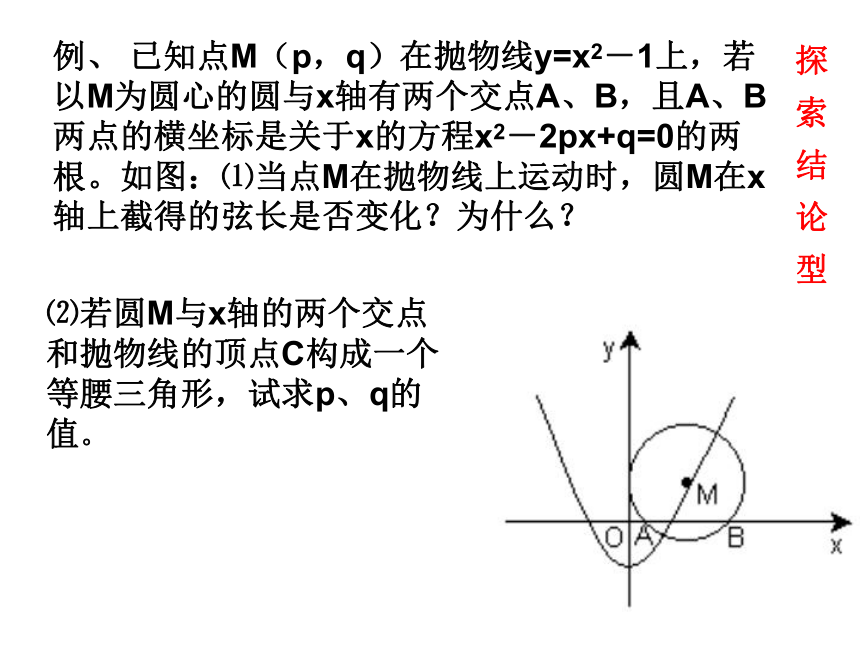
论,然后再进行论证。例、 已知点M(p,q)在抛物线y=x2-1上,若以M为圆心的圆与x轴有两个交点A、B,且A、B两点的横坐标是关于x的方程x2-2px+q=0的两根。如图:⑴当点M在抛物线上运动时,圆M在x轴上截得的弦长是否变化?为什么?探 索 结 论 型⑵若圆M与x轴的两个交点
和抛物线的顶点C构成一个
等腰三角形,试求p、q的
值。
考点3、存在探索型存在探索型问题是指在给定条件下,判断某种数学
现象是否存在、某个结论是否出现的问题,解决这
类问题的一般思路是:先假设结论的某一 方面存在,
然后在这个假设下进行演绎推理,若推出矛盾,即
可否定假设;若推出合理结论,则可肯定假设。
例3、如图,二次函数y=x2-4x+3的图象与x轴交于A、B两点,顶点为C。
⑴求A、B、C三点的坐标;
探 索 存 在 型探索存在性问题的方法,一般都是先假设存在,在此前提下进行推理.当出现矛盾时,否定假设,从而假设不存在.
⑵在y轴上求作一点P(不写作法)使得PA+PC最小,并求P点的坐标;⑶在x轴上方的抛物线上,是否存在点Q,使得以A、B、Q三点为顶点的三
角形与△ABC相似?如果存在,求出
Q点的坐标;如果不存在,请说明不
存在的理由。例4、如图,所示,已知△ABC中,AB=4,D在AB边上移动(不与A、B重合),DE∥BC交AC于E点,连接CD。设S△ABC=S,S△DEC=S1,(1)当D点为AB中点时,求S1︰S的值。(2)若AD=x, S1︰S=y,求y关于x的函数关系式及自变量x的取值范围。(3)是否存在点D,使S1> S得成立?若存在,求出D点位置,若不存在,请说明理由存在型探索探索存在性问题的方法,一般都是先假设存在,在此前提下进行推理.当出现矛盾时,否定假设,从而假设不存在.考点4、规律探索型规律探索型问题是指由给出的几个具体的结论来探求与它相关的一般性的结论的问题,解决这类问题的一般思路是:通过对所给的具体的结论进行全面而细致的观察、分析、比较、从中发现其变化规律,并由此猜想出一般性的结论,然后再给出合理的证明或加以应用。考点5、决策探索型决策探索型问题是指必须对题目给出的几种可能方案
作出合理选择的一类“优选”问题,解决这类问题的一
般思路是:通过对题设信息进行全面的分析,综合比
较,判断优劣,从中寻找出适合题意的最佳方案考点6、一类规律探索探索题的解决在含有两个变量的探索过程中,可用函数的方法解决,
方法如下:
(1)列表:根据题意确定两个变量并列表;
(2)猜想函数关系式,一般可先尝试一次函数关系式或
二次函数关系式
(3)求所设关系式,一般用小数据代入,用待定系数法
(4)验证所得关系式
(一)条件开放或探索
例.(2007南京市)已知点位于第二象限,并且,为整数,写出一个符合上述条件的点的坐标: .
答;(-1,3),(-1,2),(-1,1),
(-2,1),(-2,2)六个中任意写出一个即可.
例(2007呼和浩特市)在四边形ABCD中,顺次连接四边中点E,F,G,H,构成一个新的四边形,请你对四边形ABCD填加一个条件,使四边形EFGH成为一个菱形.这个条件是 .
解:或四边形是等腰梯形(符合要求的其它答案也可以) (二)结论开放或探索
例(05湖南湘潭)如图,在△ABC中,AB=AC,AD⊥BC,D为垂足。由以上两个条件可得________。(写出一个结论)
解:∠1=∠2或BD=DC或△ABD≌△ACD等。
例(2007自贡)一个叫巴尔末的中学教师成功地从光谱数据 中得到巴尔末公式,从而打
开了光谱奥秘的大门,请你按照这种规律,写出第n(n≥1)个数据是________或___. 例(2007云南省)已知:如图,四边形ABCD是矩形(AD>AB),点E在BC上,且AE =AD,DF⊥AE,垂足为F. 请探求DF与AB有何数量关系?写出你所得到的结论并给予证明.
解:经探求,结论是:DF = AB.
证明如下:∵四边形ABCD是矩形,
∴ ∠B =90° , AD∥BC,
∴ ∠DAF = ∠AEB.
∵ DF⊥AE, ∴ ∠AFD = 90° ,
∵ AE = AD ,∴ ABE ≌DFA.∴ AB = DF.
逆向推理,逐步探寻结论成立的充分条件,或把可能
产生结论的条件一一列出,逐个分析考察,答案不唯一例1、在梯形ABCD中,AB∥CD,E、F、G、H分别是
边AB,BC,CD,DA的中点,要使EFGH是菱形,则
下列补充条件中不正确的是( )
(A)AC⊥BD;(B)AC = BD;
(C)AD = BC;(D)∠D = ∠C例2、已知:△ABC中,∠ABC = 450,H是高AD和BE的交点,求证:(1)BH = AC,(图1)条 件 探 索 (2)现将原题图中的∠A改成钝角,题设条件不变。请你按题设要求在钝角三角形ABC(图2)中画出该题的图形(3)∠A改成钝角后、结论BH = AC还成立吗 ?若成立、请证明;若不成立、请说明理由。
答:BH=AC还成立
证明:∵HD,CE是高,∴∠1=∠2=∠3=900
∴∠5+∠C=900 ,∠4+∠H=900
∵∠4=∠5,∴∠H=∠C
∵∠1=900,∠ABC=450,∴∠6=∠ABC=450
∴BD=AD
∴△HBD≌△CAD
∴BH=AC 考点2、结论探索型 猜想型,需探索的结论需要依据题设条件从简单
情况或特殊情况入手进行归纳,大胆猜想得出结
论,然后再进行论证。例、 已知点M(p,q)在抛物线y=x2-1上,若以M为圆心的圆与x轴有两个交点A、B,且A、B两点的横坐标是关于x的方程x2-2px+q=0的两根。如图:⑴当点M在抛物线上运动时,圆M在x轴上截得的弦长是否变化?为什么?探 索 结 论 型⑵若圆M与x轴的两个交点
和抛物线的顶点C构成一个
等腰三角形,试求p、q的
值。
考点3、存在探索型存在探索型问题是指在给定条件下,判断某种数学
现象是否存在、某个结论是否出现的问题,解决这
类问题的一般思路是:先假设结论的某一 方面存在,
然后在这个假设下进行演绎推理,若推出矛盾,即
可否定假设;若推出合理结论,则可肯定假设。
例3、如图,二次函数y=x2-4x+3的图象与x轴交于A、B两点,顶点为C。
⑴求A、B、C三点的坐标;
探 索 存 在 型探索存在性问题的方法,一般都是先假设存在,在此前提下进行推理.当出现矛盾时,否定假设,从而假设不存在.
⑵在y轴上求作一点P(不写作法)使得PA+PC最小,并求P点的坐标;⑶在x轴上方的抛物线上,是否存在点Q,使得以A、B、Q三点为顶点的三
角形与△ABC相似?如果存在,求出
Q点的坐标;如果不存在,请说明不
存在的理由。例4、如图,所示,已知△ABC中,AB=4,D在AB边上移动(不与A、B重合),DE∥BC交AC于E点,连接CD。设S△ABC=S,S△DEC=S1,(1)当D点为AB中点时,求S1︰S的值。(2)若AD=x, S1︰S=y,求y关于x的函数关系式及自变量x的取值范围。(3)是否存在点D,使S1> S得成立?若存在,求出D点位置,若不存在,请说明理由存在型探索探索存在性问题的方法,一般都是先假设存在,在此前提下进行推理.当出现矛盾时,否定假设,从而假设不存在.考点4、规律探索型规律探索型问题是指由给出的几个具体的结论来探求与它相关的一般性的结论的问题,解决这类问题的一般思路是:通过对所给的具体的结论进行全面而细致的观察、分析、比较、从中发现其变化规律,并由此猜想出一般性的结论,然后再给出合理的证明或加以应用。考点5、决策探索型决策探索型问题是指必须对题目给出的几种可能方案
作出合理选择的一类“优选”问题,解决这类问题的一
般思路是:通过对题设信息进行全面的分析,综合比
较,判断优劣,从中寻找出适合题意的最佳方案考点6、一类规律探索探索题的解决在含有两个变量的探索过程中,可用函数的方法解决,
方法如下:
(1)列表:根据题意确定两个变量并列表;
(2)猜想函数关系式,一般可先尝试一次函数关系式或
二次函数关系式
(3)求所设关系式,一般用小数据代入,用待定系数法
(4)验证所得关系式
(一)条件开放或探索
例.(2007南京市)已知点位于第二象限,并且,为整数,写出一个符合上述条件的点的坐标: .
答;(-1,3),(-1,2),(-1,1),
(-2,1),(-2,2)六个中任意写出一个即可.
例(2007呼和浩特市)在四边形ABCD中,顺次连接四边中点E,F,G,H,构成一个新的四边形,请你对四边形ABCD填加一个条件,使四边形EFGH成为一个菱形.这个条件是 .
解:或四边形是等腰梯形(符合要求的其它答案也可以) (二)结论开放或探索
例(05湖南湘潭)如图,在△ABC中,AB=AC,AD⊥BC,D为垂足。由以上两个条件可得________。(写出一个结论)
解:∠1=∠2或BD=DC或△ABD≌△ACD等。
例(2007自贡)一个叫巴尔末的中学教师成功地从光谱数据 中得到巴尔末公式,从而打
开了光谱奥秘的大门,请你按照这种规律,写出第n(n≥1)个数据是________或___. 例(2007云南省)已知:如图,四边形ABCD是矩形(AD>AB),点E在BC上,且AE =AD,DF⊥AE,垂足为F. 请探求DF与AB有何数量关系?写出你所得到的结论并给予证明.
解:经探求,结论是:DF = AB.
证明如下:∵四边形ABCD是矩形,
∴ ∠B =90° , AD∥BC,
∴ ∠DAF = ∠AEB.
∵ DF⊥AE, ∴ ∠AFD = 90° ,
∵ AE = AD ,∴ ABE ≌DFA.∴ AB = DF.
