数学人教A版(2019)必修第一册3.2.2奇偶性(共46张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册3.2.2奇偶性(共46张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 20:30:51 | ||
图片预览








文档简介
(共46张PPT)
3.2 函数的奇偶性
不仅生活中有对称美,函数图像也具有对称性。
今天让我们从函数图象的对称性出发,一起探究函数的奇偶性
思考:观察函数的图象,你能发现这两个函数图像有什么共同特征吗
两个函数的图像都关于y轴对称
思考:类比函数的单调性,如何用符号语言精确地描述“函数图像关于y轴对称”这一特征?
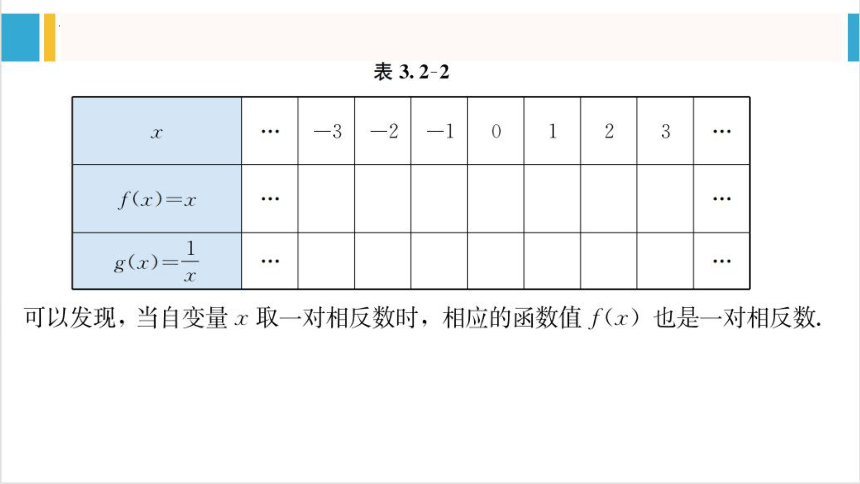
…
思考:类比函数的单调性,如何用符号语言精确地描述“函数图像关于y轴对称”这一特征?
当自变量取一对相反数时,
相应的两个函数值相等。
9 4 1 1 4 9
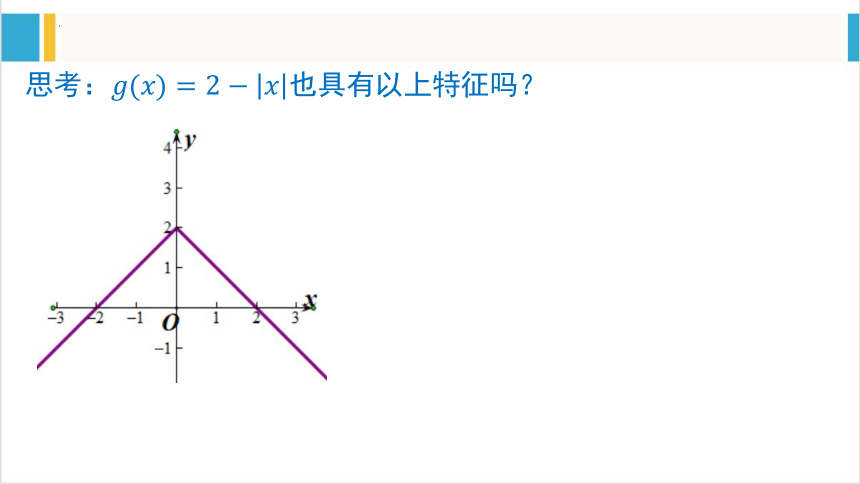
也具有以上特征吗?
…
1、定义: 一般地,设函数的定义域为 ,如果,都有,且,那么函数就叫做偶函数。
一、偶函数
2、偶函数的图象特征:图象关于轴对称
思考1:是偶函数吗?
思考2:偶函数的定义域有何特征?
定义域关于原点对称
思考3:对于定义在R上的函数,若,那么这个函数是偶函数吗?
不是
不是
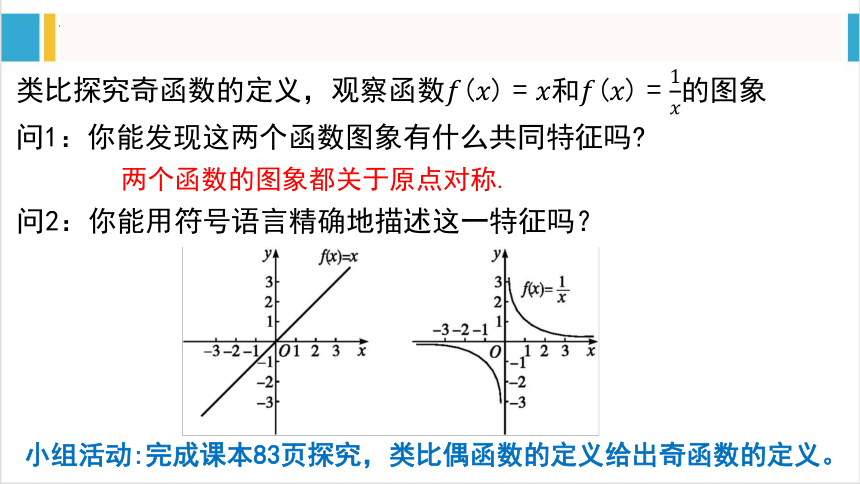
类比探究奇函数的定义,观察函数和的图象 问1:你能发现这两个函数图象有什么共同特征吗
小组活动:完成课本83页探究,类比偶函数的定义给出奇函数的定义。
问2:你能用符号语言精确地描述这一特征吗?
两个函数的图象都关于原点对称.
1、定义:一般地,设函数的定义域为 ,如果,都有,且,那么函数就叫做奇函数。
二、偶函数
2、奇函数的图象特征:图象关于轴对称
定义域关于原点对称
1、判断下列说法是否正确.
(1)对于函数,若存在,使0,则函数一定是奇函数. ( )
(2)函数是奇函数. ( )
(3)奇函数与偶函数的定义域都关于原点对称 ( )
×
×
思考:我们接触过奇函数、偶函数、既不是奇函数也不是偶函数的函数,那么是否存在既是奇函数又是偶函数的函数呢?
(4)已知奇函数在)有最大值,则在上有最小值. ( )
题型一:概念理解
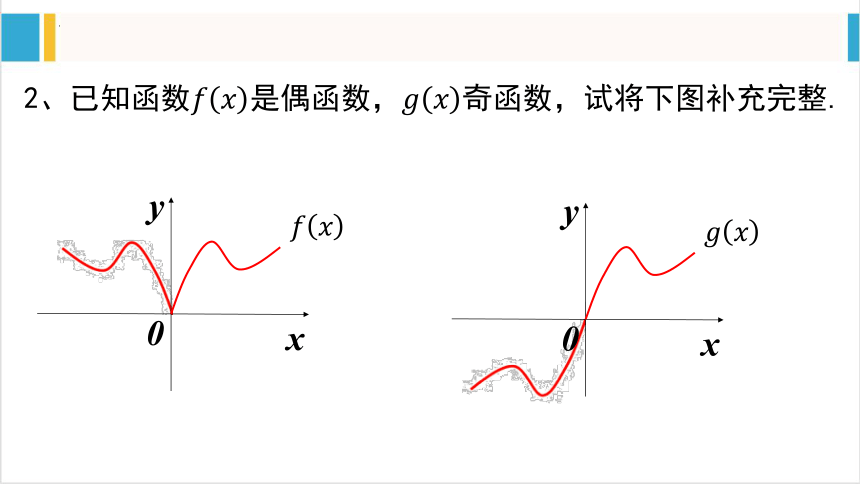
2、已知函数是偶函数,奇函数,试将下图补充完整.
x
y
0
x
y
0
例1:观察下列函数图像,并判断它们的奇偶性
偶函数
奇函数
奇函数
非奇非偶
非奇非偶
非奇非偶
图象法
题型二:判断函数的奇偶性
例2:判断下列函数的奇偶性并证明
定义法
(1)
(2)
(3)
(4)
偶函数
奇函数
奇函数
偶函数
一看定义域
二看关系式or图象
不关于原点对称
关于原点对称
非奇非偶函数
f(﹣x)=f(x)
图象关于y轴对称
f(﹣x)=﹣f(x)
图象关于原点对称
偶函数
奇函数
既奇又偶函数
定义法
练习:下列判断不正确的是__________.
①④
是奇函数
例3:已知f(x),g(x)是R上的奇函数,试判断f(x)+g(x),f(x)g(x)的奇偶性.
解:因为f(-x)+g(-x)=-(f(x)+g(x))
所以y=f(x)+g(x)是R上的奇函数;
因为f(-x)g(-x)=(-f(x))(-g(x))=f(x)g(x)
所以y=f(x)g(x)是R上的偶函数;
f(x) g(x) f(x)+g(x) f(x)-g(x) f(x)·g(x)
偶 偶 偶 偶 偶
偶 奇 不确定 不确定 奇
奇 偶 不确定 不确定 奇
奇 奇 奇 奇 偶
1、定义法
①确定定义域,并观察定义域是否关于原点对称.
②计算,并比较与的关系.
③若,则为奇函数,其图像关于原点对称;
若,则为偶函数,其图像关于y轴对称.
2、图象法(对称)
3、性质法(不研究的情况)
①奇奇=奇;偶偶=偶;②奇奇=偶;奇偶=奇;偶偶=偶;
题型二:判断函数的奇偶性
已知奇偶性可代特殊值求参数
4
0
1
-1
1、利用奇偶性反求参数
题型三:函数奇偶性的应用
B
变式:已知是定义在上的奇函数,则_____________.
2
f(x)为奇函数且x=0处有定义,则f(0)=0
题型三:函数奇偶性的应用
2、利用函数的奇偶性求函数的解析式
例题:f(x)是R上的偶函数,且x∈(0,+∞)时,f(x)=x2+x-1,
① 求f(-2)的值. ②求x∈(-∞,0)时, f(x)的解析式.
[变式]f(x)是R上的奇函数,且x<0时,f(x)=x2-2x+3,求f(x)在R上的解析式.
解:①因为f(x)是R上的偶函数,所以f(-2)=f(2)=5
题型三:函数奇偶性的应用
[变式]f(x)是R上的奇函数,且x<0时,f(x)=x2-2x+3,求f(x)在R上的解析式.
练习:设是偶函数,是奇函数,且+=,求函数,的解析式
例题:已知f(x)=ax3-bx(a,b∈R), f(m)=5, 则f(-m)= .
4
3、利用函数的奇偶性求函数的值
题型三:函数奇偶性的应用
变式:已知f(x)=ax3-bx+4(a,b∈R), f(m)=5, 则f(-m)= .
3
-5
4、函数的奇偶性与单调性
例题:已知是偶函数且在上单调递减,则____
>
偶函数在对称区间上单调性相反
奇函数在对称区间上单调性相同
练习:已知函数的局部图像如图,求函数的单调区间.
为偶函数
为奇函数
单调递增区间:
单调递减区间:
[-1,0],[1,+∞)
[0,1],(-∞,-1]
单调递增区间:
单调递减区间:
(-∞,-1],[1,+∞)
[-1,0],[0,1]
总结:奇函数与偶函数的性质:
①且 ②
③(若最值存在,则有)
④原点两侧单调性相同
2、若已知是上的奇函数,则可得:
1、若已知是上的偶函数,则可得:
①且
②;
③原点两侧单调性相反
例题:若对于任意实数总有,且在区间上是增函数,则( )
解:据题意得:为偶函数,且在区间上是增函数.
∴.
又∵
∴,即.
1、利用函数的性质比较大小
题型四:函数性质的综合应用
B
例题:定义在[-5,5]上的奇函数f(x)部分图象如图,则不等式f(x)>0的解集为_____________.
2、利用函数的性质解不等式
题型三:函数奇偶性的应用
(-5,-2)(0,2)
变式:定义在[-5,5]上的奇函数f(x)部分图象如图,则不等式x f(x)>0的解集为_____________.
(-2,0)∪(0,2)
例2:函数y=f(x)是R上的偶函数, 且在(-∞,0]上为增函数, 若f(a)≤f(2), 则实数a的取值范围是_____________.
变式:函数y=g(x)是定义在[-2,2]上的偶函数,当x≥0时,g(x)单调递增,若g(1-m)练习:函数f(x)是定义在[-2,2]上的奇函数,且在区间[0,2]上单调递减,若f(m)+f(m-1)>0,求实数m的取值范围.
练习:函数f(x)是定义在[-2,2]上的奇函数,且在区间[0,2]上单调递减,若f(m)+f(m-1)>0,求实数m的取值范围.
变式:函数y=g(x)是定义在[-2,2]上的偶函数,当x≥0时,g(x)单调递增,若g(1-m)题型五:抽象函数问题
练习:已知函数的定义域为,且满足条件:①;②;③当时,
(1)求和的值;
(2)判断函数的奇偶性;
(3)讨论函数的单调性;
(4)求不等式的解集.
题型五:抽象函数问题
题型六:对称性
思考:若函数是偶函数,则函数的图象有何特征?
思考:若函数是偶函数,则函数的图象有何特征?
思考:若函数的图象关于直线对称,则函数满足什么关系式?
1、若函数是偶函数,则函数的图象关于直线对称;
若函数是奇函数,则函数的图象关于点(,0)中心对称;
2、若对于R上的任意都有或
或,则的图象关于直线对称.
若对于R上的任意都有或
或,则的图象关于点(,0)对称.
题型六:对称性
B
D
3.2 函数的奇偶性
不仅生活中有对称美,函数图像也具有对称性。
今天让我们从函数图象的对称性出发,一起探究函数的奇偶性
思考:观察函数的图象,你能发现这两个函数图像有什么共同特征吗
两个函数的图像都关于y轴对称
思考:类比函数的单调性,如何用符号语言精确地描述“函数图像关于y轴对称”这一特征?
…
思考:类比函数的单调性,如何用符号语言精确地描述“函数图像关于y轴对称”这一特征?
当自变量取一对相反数时,
相应的两个函数值相等。
9 4 1 1 4 9
也具有以上特征吗?
…
1、定义: 一般地,设函数的定义域为 ,如果,都有,且,那么函数就叫做偶函数。
一、偶函数
2、偶函数的图象特征:图象关于轴对称
思考1:是偶函数吗?
思考2:偶函数的定义域有何特征?
定义域关于原点对称
思考3:对于定义在R上的函数,若,那么这个函数是偶函数吗?
不是
不是
类比探究奇函数的定义,观察函数和的图象 问1:你能发现这两个函数图象有什么共同特征吗
小组活动:完成课本83页探究,类比偶函数的定义给出奇函数的定义。
问2:你能用符号语言精确地描述这一特征吗?
两个函数的图象都关于原点对称.
1、定义:一般地,设函数的定义域为 ,如果,都有,且,那么函数就叫做奇函数。
二、偶函数
2、奇函数的图象特征:图象关于轴对称
定义域关于原点对称
1、判断下列说法是否正确.
(1)对于函数,若存在,使0,则函数一定是奇函数. ( )
(2)函数是奇函数. ( )
(3)奇函数与偶函数的定义域都关于原点对称 ( )
×
×
思考:我们接触过奇函数、偶函数、既不是奇函数也不是偶函数的函数,那么是否存在既是奇函数又是偶函数的函数呢?
(4)已知奇函数在)有最大值,则在上有最小值. ( )
题型一:概念理解
2、已知函数是偶函数,奇函数,试将下图补充完整.
x
y
0
x
y
0
例1:观察下列函数图像,并判断它们的奇偶性
偶函数
奇函数
奇函数
非奇非偶
非奇非偶
非奇非偶
图象法
题型二:判断函数的奇偶性
例2:判断下列函数的奇偶性并证明
定义法
(1)
(2)
(3)
(4)
偶函数
奇函数
奇函数
偶函数
一看定义域
二看关系式or图象
不关于原点对称
关于原点对称
非奇非偶函数
f(﹣x)=f(x)
图象关于y轴对称
f(﹣x)=﹣f(x)
图象关于原点对称
偶函数
奇函数
既奇又偶函数
定义法
练习:下列判断不正确的是__________.
①④
是奇函数
例3:已知f(x),g(x)是R上的奇函数,试判断f(x)+g(x),f(x)g(x)的奇偶性.
解:因为f(-x)+g(-x)=-(f(x)+g(x))
所以y=f(x)+g(x)是R上的奇函数;
因为f(-x)g(-x)=(-f(x))(-g(x))=f(x)g(x)
所以y=f(x)g(x)是R上的偶函数;
f(x) g(x) f(x)+g(x) f(x)-g(x) f(x)·g(x)
偶 偶 偶 偶 偶
偶 奇 不确定 不确定 奇
奇 偶 不确定 不确定 奇
奇 奇 奇 奇 偶
1、定义法
①确定定义域,并观察定义域是否关于原点对称.
②计算,并比较与的关系.
③若,则为奇函数,其图像关于原点对称;
若,则为偶函数,其图像关于y轴对称.
2、图象法(对称)
3、性质法(不研究的情况)
①奇奇=奇;偶偶=偶;②奇奇=偶;奇偶=奇;偶偶=偶;
题型二:判断函数的奇偶性
已知奇偶性可代特殊值求参数
4
0
1
-1
1、利用奇偶性反求参数
题型三:函数奇偶性的应用
B
变式:已知是定义在上的奇函数,则_____________.
2
f(x)为奇函数且x=0处有定义,则f(0)=0
题型三:函数奇偶性的应用
2、利用函数的奇偶性求函数的解析式
例题:f(x)是R上的偶函数,且x∈(0,+∞)时,f(x)=x2+x-1,
① 求f(-2)的值. ②求x∈(-∞,0)时, f(x)的解析式.
[变式]f(x)是R上的奇函数,且x<0时,f(x)=x2-2x+3,求f(x)在R上的解析式.
解:①因为f(x)是R上的偶函数,所以f(-2)=f(2)=5
题型三:函数奇偶性的应用
[变式]f(x)是R上的奇函数,且x<0时,f(x)=x2-2x+3,求f(x)在R上的解析式.
练习:设是偶函数,是奇函数,且+=,求函数,的解析式
例题:已知f(x)=ax3-bx(a,b∈R), f(m)=5, 则f(-m)= .
4
3、利用函数的奇偶性求函数的值
题型三:函数奇偶性的应用
变式:已知f(x)=ax3-bx+4(a,b∈R), f(m)=5, 则f(-m)= .
3
-5
4、函数的奇偶性与单调性
例题:已知是偶函数且在上单调递减,则____
>
偶函数在对称区间上单调性相反
奇函数在对称区间上单调性相同
练习:已知函数的局部图像如图,求函数的单调区间.
为偶函数
为奇函数
单调递增区间:
单调递减区间:
[-1,0],[1,+∞)
[0,1],(-∞,-1]
单调递增区间:
单调递减区间:
(-∞,-1],[1,+∞)
[-1,0],[0,1]
总结:奇函数与偶函数的性质:
①且 ②
③(若最值存在,则有)
④原点两侧单调性相同
2、若已知是上的奇函数,则可得:
1、若已知是上的偶函数,则可得:
①且
②;
③原点两侧单调性相反
例题:若对于任意实数总有,且在区间上是增函数,则( )
解:据题意得:为偶函数,且在区间上是增函数.
∴.
又∵
∴,即.
1、利用函数的性质比较大小
题型四:函数性质的综合应用
B
例题:定义在[-5,5]上的奇函数f(x)部分图象如图,则不等式f(x)>0的解集为_____________.
2、利用函数的性质解不等式
题型三:函数奇偶性的应用
(-5,-2)(0,2)
变式:定义在[-5,5]上的奇函数f(x)部分图象如图,则不等式x f(x)>0的解集为_____________.
(-2,0)∪(0,2)
例2:函数y=f(x)是R上的偶函数, 且在(-∞,0]上为增函数, 若f(a)≤f(2), 则实数a的取值范围是_____________.
变式:函数y=g(x)是定义在[-2,2]上的偶函数,当x≥0时,g(x)单调递增,若g(1-m)
练习:函数f(x)是定义在[-2,2]上的奇函数,且在区间[0,2]上单调递减,若f(m)+f(m-1)>0,求实数m的取值范围.
变式:函数y=g(x)是定义在[-2,2]上的偶函数,当x≥0时,g(x)单调递增,若g(1-m)
练习:已知函数的定义域为,且满足条件:①;②;③当时,
(1)求和的值;
(2)判断函数的奇偶性;
(3)讨论函数的单调性;
(4)求不等式的解集.
题型五:抽象函数问题
题型六:对称性
思考:若函数是偶函数,则函数的图象有何特征?
思考:若函数是偶函数,则函数的图象有何特征?
思考:若函数的图象关于直线对称,则函数满足什么关系式?
1、若函数是偶函数,则函数的图象关于直线对称;
若函数是奇函数,则函数的图象关于点(,0)中心对称;
2、若对于R上的任意都有或
或,则的图象关于直线对称.
若对于R上的任意都有或
或,则的图象关于点(,0)对称.
题型六:对称性
B
D
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
