数学人教A版(2019)选择性必修第一册2.3.1两条直线的交点坐标 课件(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.3.1两条直线的交点坐标 课件(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 444.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-22 20:40:42 | ||
图片预览







文档简介
(共20张PPT)
2.3.1两条直线的交点坐标
第二章 直线和圆的方程
高二数学备课组
2.3 直线的交点坐标与距离公式
问题1:已知直线 ,
相交,如何求得两条直线的交点坐标?
即为两条直线交点坐标.
联立方程组
解得
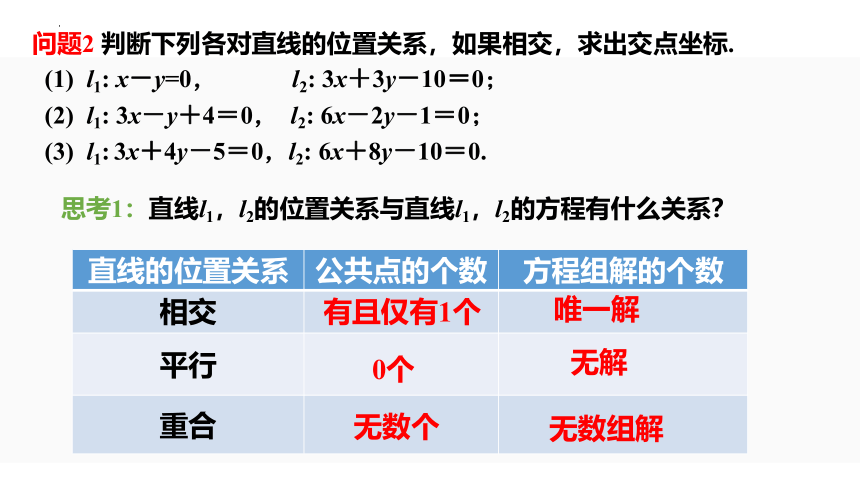
问题2 判断下列各对直线的位置关系,如果相交,求出交点坐标.
(1) l1: x-y=0, l2: 3x+3y-10=0;
(2) l1: 3x-y+4=0, l2: 6x-2y-1=0;
(3) l1: 3x+4y-5=0,l2: 6x+8y-10=0.
思考1:直线l1,l2的位置关系与直线l1,l2的方程有什么关系?
直线的位置关系 公共点的个数 方程组解的个数
相交
平行
重合
有且仅有1个
唯一解
0个
无解
无数个
无数组解
一般地,对于直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0(A1B1C1≠0,A2B2C2≠0),有方程组
练1 已知直线5x+4y=2a+1与直线2x+3y=a的交点位于第四象
限,则a的取值范围是_________.
变式 已知直线5x+4y=2a+1与直线2x+3y=a的交点位于y轴,则a的取值是_________.
x
y
O
几何意义:
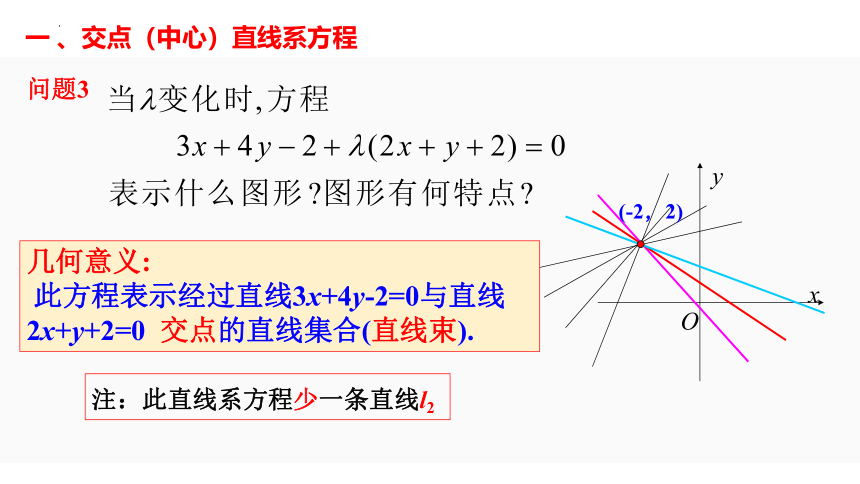
此方程表示经过直线3x+4y-2=0与直线2x+y+2=0 交点的直线集合(直线束).
注:此直线系方程少一条直线l2
一 、交点(中心)直线系方程
问题 3
(-2,2)
过两条已知直线A1x+B1y+C1=0,A2x+B2y+C2=0交点的直线系方程为
A1x+B1y+C1+λ(A2x+B2y+C2)=0(不包括直线A2x+B2y+C2=0).
类型一 恒过定点问题
分离参数法:
2.已知实数m,n满足m-n=1,求直线(m+1)x-ny-2m=0过定点
类型一 恒过定点问题
例3 已知直线l经过直线2x-y-1=0和x+3y - 11=0的交点P
(1)若直线l过原点,求直线l的方程;
(2)若直线l过点(4,5),求直线l的方程;
(3)若直线l与直线3x - y + 2=0平行,求直线l的方程.
(4)若直线l与直线3x - y + 2=0垂直,求直线l的方程.
(5)若直线l在坐标轴上的截距相等,求直线l的方程.
类型二 过定点的直线
(1)求过两直线交点的直线方程的方法
①方程组法:一般是先解方程组求出两直线的交点坐标,再结合其他条件求出直线方程.
②直线系法:过两条已知直线A1x+B1y+C1=0,A2x+B2y+C2=0交点的直线系方程为
A1x+B1y+C1+λ(A2x+B2y+C2)=0(不包括直线A2x+B2y+C2=0).
方法总结:
例2. 过两直线l1:x-3y+4=0和l2:2x+y+5=0的交点和原点的直线方程为____________.
类型二 过定点的直线
例2. 过两直线l1:x-3y+4=0和l2:2x+y+5=0的交点和原点的直线方程为____________.
3x+19y=0
类型二 交点(中心)直线系方程
类型二 交点(中心)直线系方程
例3 过点P(3,0)作一直线分别交直线2x-y-2=0和x+y+3=0于点A,B,且点P恰好为线段AB的中点,求此直线的方程.
类型三 已知中点的两点坐标设法
分析二:设出A(x1,y1),由P(3,0)为AB的中点,易求出B的坐标,而点B在另一直线上,从而求出x1、y1的值,再由两点式求直线的方程.
解法二:设A点坐标为(x1,y1),则由P(3,0)为线段AB的中点,得B点坐标为(6-x1,-y1).
∵点A,B分别在已知两直线上,
类型四 利用位置关系求参数的值
【思路分析】 根据围成三角形的条件:任何两条直线不平行,三条直线不共点.本题是关于位置关系的讨论问题.
类型三 利用位置关系求参数的值
【思路分析】 根据围成三角形的条件:任何两条直线不平行,三条直线不共点.本题是关于位置关系的讨论问题.
1. 两条直线的交点坐标:
一般地,将两条直线的方程联立,得方程组
若方程组有唯一解,则直线l1 与 l2 相交,方程组的解就是交点的坐标.
2.直线系:
具有某一共同属性的一类直线的集合.
共点(中心)直线系方程:
经过两直线l1: A1x+B1y+C1=0,l2: A2x+B2y+C2=0交点的直线系方程是A1x+B1y+C1+λ(A2x+B2y+C2)=0,其中λ是参变量,它不表示直线 l2 .
THANKS
2.3.1两条直线的交点坐标
第二章 直线和圆的方程
高二数学备课组
2.3 直线的交点坐标与距离公式
问题1:已知直线 ,
相交,如何求得两条直线的交点坐标?
即为两条直线交点坐标.
联立方程组
解得
问题2 判断下列各对直线的位置关系,如果相交,求出交点坐标.
(1) l1: x-y=0, l2: 3x+3y-10=0;
(2) l1: 3x-y+4=0, l2: 6x-2y-1=0;
(3) l1: 3x+4y-5=0,l2: 6x+8y-10=0.
思考1:直线l1,l2的位置关系与直线l1,l2的方程有什么关系?
直线的位置关系 公共点的个数 方程组解的个数
相交
平行
重合
有且仅有1个
唯一解
0个
无解
无数个
无数组解
一般地,对于直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0(A1B1C1≠0,A2B2C2≠0),有方程组
练1 已知直线5x+4y=2a+1与直线2x+3y=a的交点位于第四象
限,则a的取值范围是_________.
变式 已知直线5x+4y=2a+1与直线2x+3y=a的交点位于y轴,则a的取值是_________.
x
y
O
几何意义:
此方程表示经过直线3x+4y-2=0与直线2x+y+2=0 交点的直线集合(直线束).
注:此直线系方程少一条直线l2
一 、交点(中心)直线系方程
问题 3
(-2,2)
过两条已知直线A1x+B1y+C1=0,A2x+B2y+C2=0交点的直线系方程为
A1x+B1y+C1+λ(A2x+B2y+C2)=0(不包括直线A2x+B2y+C2=0).
类型一 恒过定点问题
分离参数法:
2.已知实数m,n满足m-n=1,求直线(m+1)x-ny-2m=0过定点
类型一 恒过定点问题
例3 已知直线l经过直线2x-y-1=0和x+3y - 11=0的交点P
(1)若直线l过原点,求直线l的方程;
(2)若直线l过点(4,5),求直线l的方程;
(3)若直线l与直线3x - y + 2=0平行,求直线l的方程.
(4)若直线l与直线3x - y + 2=0垂直,求直线l的方程.
(5)若直线l在坐标轴上的截距相等,求直线l的方程.
类型二 过定点的直线
(1)求过两直线交点的直线方程的方法
①方程组法:一般是先解方程组求出两直线的交点坐标,再结合其他条件求出直线方程.
②直线系法:过两条已知直线A1x+B1y+C1=0,A2x+B2y+C2=0交点的直线系方程为
A1x+B1y+C1+λ(A2x+B2y+C2)=0(不包括直线A2x+B2y+C2=0).
方法总结:
例2. 过两直线l1:x-3y+4=0和l2:2x+y+5=0的交点和原点的直线方程为____________.
类型二 过定点的直线
例2. 过两直线l1:x-3y+4=0和l2:2x+y+5=0的交点和原点的直线方程为____________.
3x+19y=0
类型二 交点(中心)直线系方程
类型二 交点(中心)直线系方程
例3 过点P(3,0)作一直线分别交直线2x-y-2=0和x+y+3=0于点A,B,且点P恰好为线段AB的中点,求此直线的方程.
类型三 已知中点的两点坐标设法
分析二:设出A(x1,y1),由P(3,0)为AB的中点,易求出B的坐标,而点B在另一直线上,从而求出x1、y1的值,再由两点式求直线的方程.
解法二:设A点坐标为(x1,y1),则由P(3,0)为线段AB的中点,得B点坐标为(6-x1,-y1).
∵点A,B分别在已知两直线上,
类型四 利用位置关系求参数的值
【思路分析】 根据围成三角形的条件:任何两条直线不平行,三条直线不共点.本题是关于位置关系的讨论问题.
类型三 利用位置关系求参数的值
【思路分析】 根据围成三角形的条件:任何两条直线不平行,三条直线不共点.本题是关于位置关系的讨论问题.
1. 两条直线的交点坐标:
一般地,将两条直线的方程联立,得方程组
若方程组有唯一解,则直线l1 与 l2 相交,方程组的解就是交点的坐标.
2.直线系:
具有某一共同属性的一类直线的集合.
共点(中心)直线系方程:
经过两直线l1: A1x+B1y+C1=0,l2: A2x+B2y+C2=0交点的直线系方程是A1x+B1y+C1+λ(A2x+B2y+C2)=0,其中λ是参变量,它不表示直线 l2 .
THANKS
