切线的性质与判定(复习课)

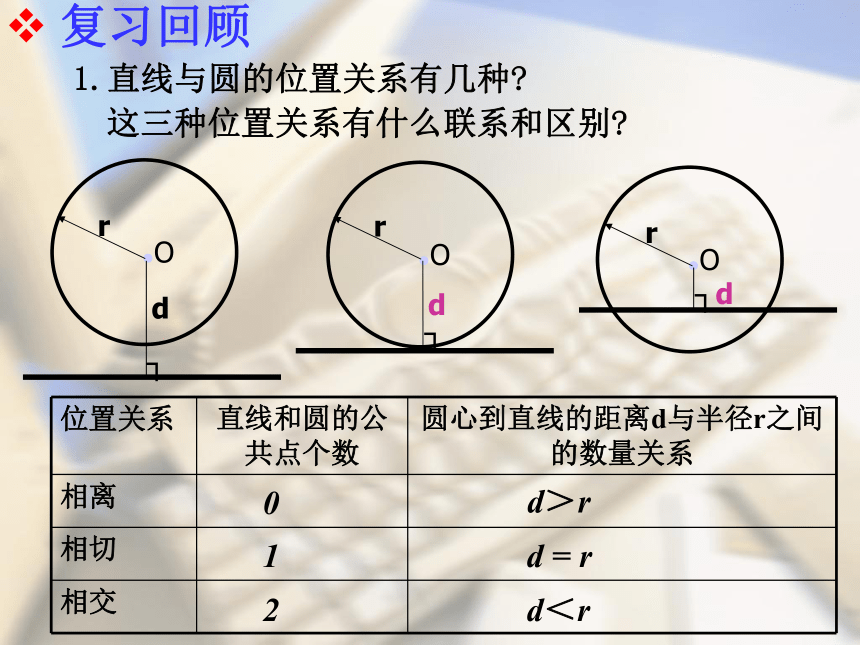
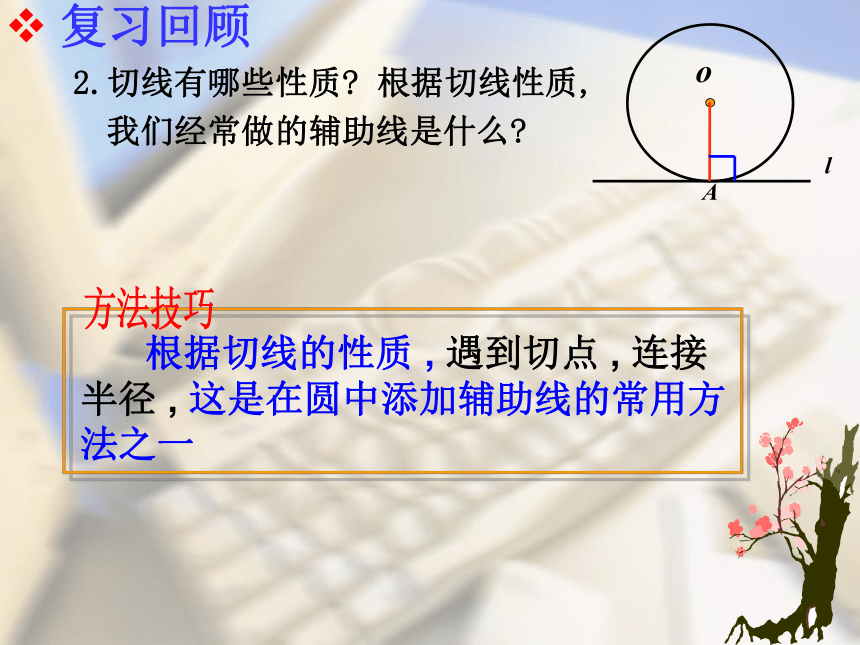
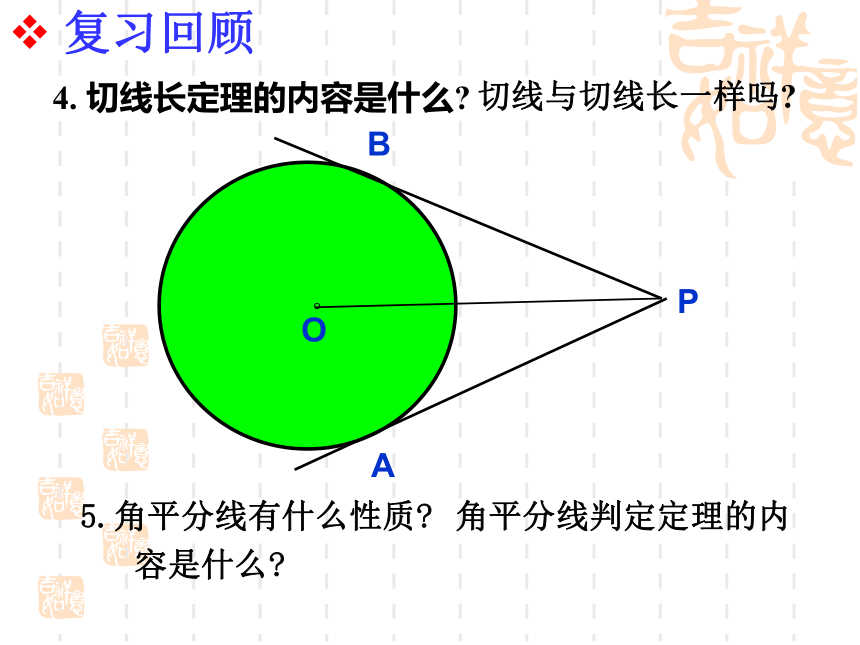
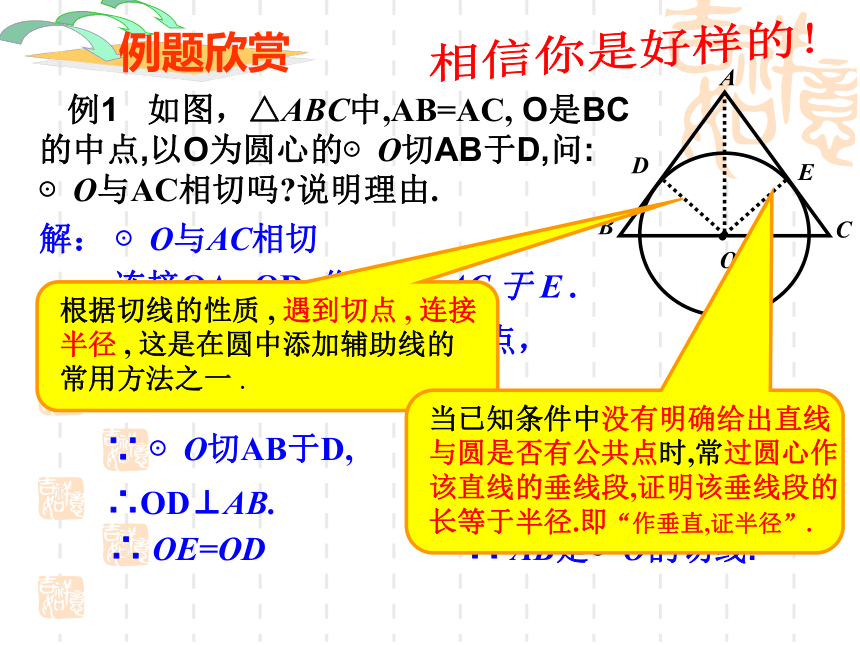
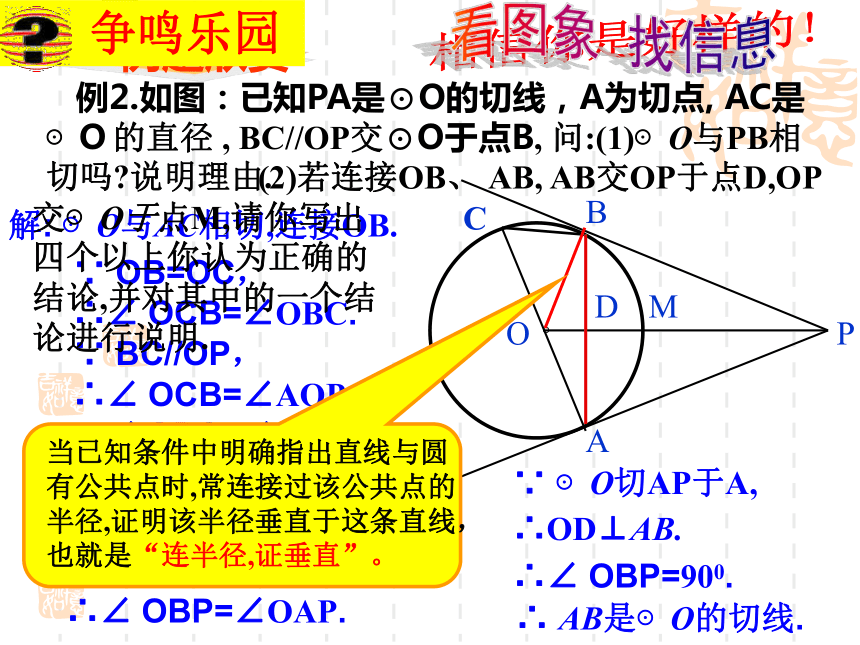
课件14张PPT。义务教育课程标准实验教科书九年级 下册华东师范大学出版社切线的性质与判定(复习课)交换一个苹果,各得一个苹果;交换一种思想,各得两种思想!1.直线与圆的位置关系有几种?d＜rd = rd＞r 复习回顾这三种位置关系有什么联系和区别?2102.切线有哪些性质? 根据切线的性质 , 遇到切点 , 连接半径 , 这是在圆中添加辅助线的常用方法之一 方法技巧 复习回顾 根据切线性质,我们经常做的辅助线是什么? 复习回顾3. 圆的切线的判定方法有哪几种? (1) 当已知条件中没有明确给出直线与圆是否有公共点时,常过圆心作该直线的垂线段,证明该垂线段的长等于半径,也就是“作垂直,证半径”。切线的判定方法 (2)当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线，也就是“连半径,证垂直”。4. 切线长定理的内容是什么? 复习回顾 切线与切线长一样吗? 5.角平分线有什么性质? 角平分线判定定理的内容是什么? 例1 如图，△ABC中,AB=AC, O是BC的中点,以O为圆心的⊙O切AB于D,问: ⊙O与AC相切吗?说明理由.解： ⊙O与AC相切∵ AB=AC ， O是BC的中点，∴AO平分∠ BAC.连接OA , OD, 作 OE⊥AC 于 E . ∴ OE=OD∵ ⊙O切AB于D,∴OD⊥AB.又∵ OE⊥AC , ∴ AB是⊙O的切线.E相信你是好样的!。PABOC 例2.如图：已知PA是⊙O的切线，A为切点, AC是⊙O 的直径 , BC//OP交⊙O于点B, 问:(1)⊙O与PB相切吗?说明理由.解: ⊙O与AC相切,连接OB.∵ OB=OC，∴∠ OCB=∠OBC. ∴ ⊿BOP ≌ ⊿AOP(SAS) ∵ ⊙O切AP于A,∴OD⊥AB.∵ BC//OP，∴∠ OCB=∠AOP. ∠ OBC=∠BOP.∴∠BOP=∠AOP.∵ OP=OP，∴∠ OBP=∠OAP.∴∠ OBP=900. ∴ AB是⊙O的切线.相信你是好样的! (2)若连接OB、 AB, AB交OP于点D,OP交⊙O于点M,请你写出 四个以上你认为正确的 结论,并对其中的一个结 论进行说明. 争鸣乐园看图象 找信息例3. 如图, 直角梯形ABCD中 , ∠A=900 , AD//BC, E为AB的中点, 以AB为直径的圆与边CD相切于点F.试猜想CE , DE的位置关系以及CD 与 AD , BC的数量关系,说明理由.F我思，我进步!解： CE⊥DE , CD=AD+BC. 连结EF∵ ∠A= 900 , ∴ AD与⊙E相切. ∵ CD与⊙E相切.∵ AD//BC ∴ ∠ADC+ ∠BCD=1800. ∴ ∠EDF+ ∠ECF=900. ∴ ∠DEC=900. ∴ CE⊥DE ∴ CD=DF+CF=AD+BC. ∴ CE⊥DE ,CD=AD+BC相信你能行!变式(一) 如图, 直角梯形ABCD中 , ∠A=900 , AD//BC, E为AB上一点,且DE平分∠ADC, CE平分∠BCD,以AB为直径的圆与边CD有怎样的位置关系? 线段CD与AD, BC之间又有怎样的关系?说明理由.解： (1)以AB为直径的圆与CD相切.∵ DE平分∠ADC, CE平分∠BCD,且∠A= ∠B= 900 ,过点E 作 EF⊥CD 于 F. ∴ 以AB为直径的圆与边CD相切.(2) CD=AD+BC.∴CD=DF+CF=AD+BC. ∴ AD=DF ∴ AD与⊙E相切.∵ ∠A= 900 , ∵ CD与⊙E相切. 同理: BC=CF相信你能行! 变式(二): 如图, 直角梯形ABCD中 , ∠A=900 , AD//BC, 且CD=AD+BC, 以AB为直径的圆与边CD有怎样的位置关系,说明理由.ABCDM解： 以AB为直径的圆与CD相切.取AB的中点E, 则点E即为以AB为直径的圆的圆心,过点E作 EF⊥CD 于 F,连接DE并延长交CB的延长线于点M
……….知识的升华独立
作业《初中数学复习方法与策略》
P103 20,21,22
祝你成功！驶向胜利的彼岸结束寄语只有不断的思考,才会有新的发现;只有量的积累,才会有质的飞跃! 谢谢！