2023-2024学年度人教版九年级数学上册23.1图形的旋转导学案(含答案)
文档属性
| 名称 | 2023-2024学年度人教版九年级数学上册23.1图形的旋转导学案(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 421.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-23 08:40:42 | ||
图片预览

文档简介
第二十三章 旋转
23.1 图形的旋转
学习目标
1.了解生活中广泛存在的旋转现象,知道旋转是继平移、对称之后的又一种基本变换.
2.能结合图形指出什么是旋转中心、旋转角和对应点.
3.体会旋转的形成过程,并探究旋转的性质.
重点:旋转及对应点的有关概念及其应用.
难点:从活生生的数学中抽出概念.
学习过程
一、创设问题情境
问题 请观察下列图形的变化(教师展示实物或图片或用课件展示):
同学们都见过风车吧,它能在风的吹动下不停地转动.在我们周围,还能看到许多转动着的物体,如车轮、水车、风力发电机、飞机的螺旋桨、时钟的指针、游乐园的大转盘……我们就生活在一个处处能见到旋转现象的世界中.
以上图形的转动有什么共同特点呢?你还能举出这样类似的生活中的情境吗?
二、自主学习
自学教材59页内容并思考:
1、你能举出生活中与旋转现象有关的例子吗?
2、它们是怎样旋转的,你能类比平移的定义概况出旋转的定义吗?
三、揭示问题规律
1.①把一个平面图形 绕着平面内某一点O转动一个角度 ,叫做图形的旋转.
②从课文中的思考实例可以看出:图形的旋转三要素是 旋转中心 , 旋转方向 , 旋转角 .
③如右图,点P是正方形ABCD内一点,将△ABP绕B点顺时针方向旋转到△CBP′的位置时,其旋转中心是 点B ,旋转角度为 90° ,点A、B、P的对应点分别为 C、B、P′ .
2.旋转作图的步骤:(1)确定旋转 中心 ,旋转 角 ,旋转 方向 ;(2)找出图形的关键点;(3)作出关键点经旋转后的 对应 点;(4)按图形的顺序连接 对应 点,得到旋转后的图形.
四、尝试应用
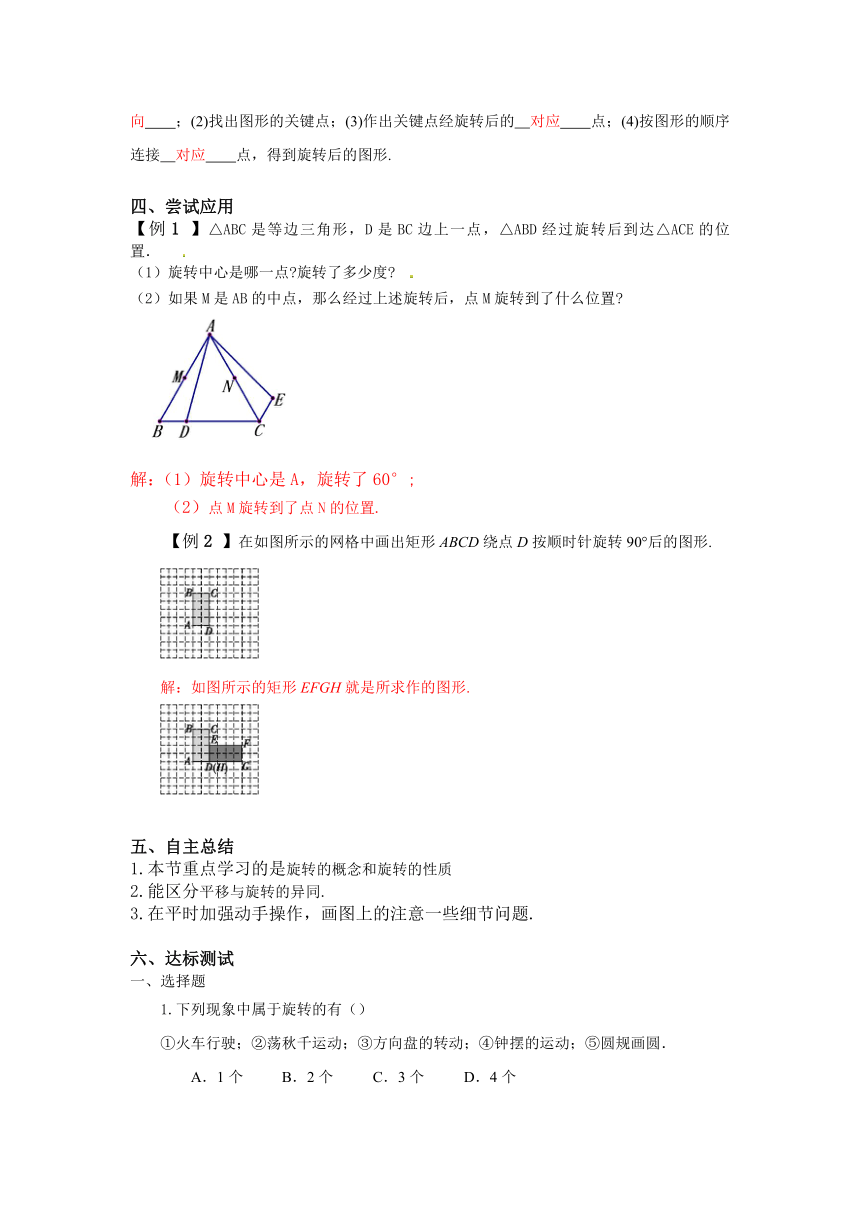
【例1 】△ABC是等边三角形,D是BC边上一点,△ABD经过旋转后到达△ACE的位置.
(1)旋转中心是哪一点 旋转了多少度
(2)如果M是AB的中点,那么经过上述旋转后,点M旋转到了什么位置
解:(1)旋转中心是A,旋转了60°;
(2)点M旋转到了点N的位置.
【例2 】在如图所示的网格中画出矩形ABCD绕点D按顺时针旋转90°后的图形.
解:如图所示的矩形EFGH就是所求作的图形.
五、自主总结
1.本节重点学习的是旋转的概念和旋转的性质
2.能区分平移与旋转的异同.
3.在平时加强动手操作,画图上的注意一些细节问题.
达标测试
一、选择题
1.下列现象中属于旋转的有()
①火车行驶;②荡秋千运动;③方向盘的转动;④钟摆的运动;⑤圆规画圆.
A.1个 B.2个 C.3个 D.4个
2.如图,在正方形网格中有△ABC,△ABC绕O点按逆时针方向旋转90°得到的图案是( )
A. B.C. D.
3.如图,在Rt△ABC中,∠BAC=90°.如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处.那么旋转的角度等于( )
A.55°B.60°C.65°D.80°
3题图 4题图
4.如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF.将△BCE绕着正方形的中心O按逆时针方向旋转到△CDF的位置,则旋转角是( )
A.45° B.60° C.90° D.120°
5.下面四个图案中,不能由基本图案(图中阴影部分)旋转得到的是( )
A. B. C. D.
二、填空题
6.如图所示,△ABC绕点A逆时针旋转某一角度得到△ADE,若∠1=∠2=∠3=20°,则旋转角为_______度.
5题图 6题图 7题图
7.如图是电脑CPU风扇的示意图.风扇共有9个叶片,每个叶片的面积约为8cm2.已知∠AOB=120°,在风扇的转动过程中,叶片落在扇形AOB内部的面积为_______cm2.
8.如图,P是正△ABC内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与P′之间的距离为PP′=_____,∠APB=______度.
9.如图,正方形ABCD中,E在BC上,△DEC按顺时针方向转动一个角度后成△DGA.
(1)图中哪一个点是旋转中心?
(2)旋转了多少度?
(3)已知CD=4,CE=3,求GE长.
23.1 图形的旋转
1.D
2.A解析:根据旋转的性质和旋转的方向得:△ABC绕O点按逆时针旋转90°后的图案是A,故选A.
3.B 解析:∵在Rt△ABC中,∠BAC=90°,将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处,∴AB1=BC,BB1=B1C,AB=AB1,∴BB1=AB=AB1,∴△ABB1是等边三角形,∴∠BAB1=60°,∴旋转的角度等于60°.
4.C 解析:连接AC、BD,AC与BD的交点即为旋转中心O.根据旋转的性质知,点C与点D对应,则∠DOC就是旋转角.∵四边形ABCD是正方形.∴∠DOC=90°.
5.D解析A、可由一个基本“花瓣”绕其中心经过7次旋转,每次旋转45°得到;
B、可由一个基本“菱形”绕其中心经过5次旋转,每次旋转60°得到;
C、可由一个基本图形绕其中心旋转180°得到;
D、不能由基本图案旋转得到.故选D.
.40 解析:∵∠1=∠2=∠3=20°,∴∠1+∠2=40°=∠BAD,即旋转角是40度.
7.24 解析:由图可知叶片落在扇形AOB内部的面积是图形面积的,因而叶片落在扇形AOB内部的面积为72×=24cm2.
8.6,150 解析:连接PP′,∵PA=6,PB=8,PC=P′B=10,∵∠PAP′=60°,∴P′A=PP′=PA=6,∴P′B=PC=10,∴∠P′PB=90°,∴∠APB=90°+60°=150°.
9.解:(1)旋转中心是点D;(2)∵△DEC按顺时针方向转动一个角度后成△DGA,∴旋转角的度数等于∠ADC的度数,∵四边形ABCD是正方形,∴∠ADC=90°,∴旋转了90°;
(3)∵四边形ABCD是正方形,∴∠B=90°,DC=AB=BC=4,∵CE=3,∴BE=4-3=1,∵△DEC按顺时针方向转动一个角度后成△DGA,∴△DEC≌△DGA,∴AG=CE=3,∴BG=3+4=7,在Rt△GBE中,GE===5.
23.1 图形的旋转
学习目标
1.了解生活中广泛存在的旋转现象,知道旋转是继平移、对称之后的又一种基本变换.
2.能结合图形指出什么是旋转中心、旋转角和对应点.
3.体会旋转的形成过程,并探究旋转的性质.
重点:旋转及对应点的有关概念及其应用.
难点:从活生生的数学中抽出概念.
学习过程
一、创设问题情境
问题 请观察下列图形的变化(教师展示实物或图片或用课件展示):
同学们都见过风车吧,它能在风的吹动下不停地转动.在我们周围,还能看到许多转动着的物体,如车轮、水车、风力发电机、飞机的螺旋桨、时钟的指针、游乐园的大转盘……我们就生活在一个处处能见到旋转现象的世界中.
以上图形的转动有什么共同特点呢?你还能举出这样类似的生活中的情境吗?
二、自主学习
自学教材59页内容并思考:
1、你能举出生活中与旋转现象有关的例子吗?
2、它们是怎样旋转的,你能类比平移的定义概况出旋转的定义吗?
三、揭示问题规律
1.①把一个平面图形 绕着平面内某一点O转动一个角度 ,叫做图形的旋转.
②从课文中的思考实例可以看出:图形的旋转三要素是 旋转中心 , 旋转方向 , 旋转角 .
③如右图,点P是正方形ABCD内一点,将△ABP绕B点顺时针方向旋转到△CBP′的位置时,其旋转中心是 点B ,旋转角度为 90° ,点A、B、P的对应点分别为 C、B、P′ .
2.旋转作图的步骤:(1)确定旋转 中心 ,旋转 角 ,旋转 方向 ;(2)找出图形的关键点;(3)作出关键点经旋转后的 对应 点;(4)按图形的顺序连接 对应 点,得到旋转后的图形.
四、尝试应用
【例1 】△ABC是等边三角形,D是BC边上一点,△ABD经过旋转后到达△ACE的位置.
(1)旋转中心是哪一点 旋转了多少度
(2)如果M是AB的中点,那么经过上述旋转后,点M旋转到了什么位置
解:(1)旋转中心是A,旋转了60°;
(2)点M旋转到了点N的位置.
【例2 】在如图所示的网格中画出矩形ABCD绕点D按顺时针旋转90°后的图形.
解:如图所示的矩形EFGH就是所求作的图形.
五、自主总结
1.本节重点学习的是旋转的概念和旋转的性质
2.能区分平移与旋转的异同.
3.在平时加强动手操作,画图上的注意一些细节问题.
达标测试
一、选择题
1.下列现象中属于旋转的有()
①火车行驶;②荡秋千运动;③方向盘的转动;④钟摆的运动;⑤圆规画圆.
A.1个 B.2个 C.3个 D.4个
2.如图,在正方形网格中有△ABC,△ABC绕O点按逆时针方向旋转90°得到的图案是( )
A. B.C. D.
3.如图,在Rt△ABC中,∠BAC=90°.如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处.那么旋转的角度等于( )
A.55°B.60°C.65°D.80°
3题图 4题图
4.如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF.将△BCE绕着正方形的中心O按逆时针方向旋转到△CDF的位置,则旋转角是( )
A.45° B.60° C.90° D.120°
5.下面四个图案中,不能由基本图案(图中阴影部分)旋转得到的是( )
A. B. C. D.
二、填空题
6.如图所示,△ABC绕点A逆时针旋转某一角度得到△ADE,若∠1=∠2=∠3=20°,则旋转角为_______度.
5题图 6题图 7题图
7.如图是电脑CPU风扇的示意图.风扇共有9个叶片,每个叶片的面积约为8cm2.已知∠AOB=120°,在风扇的转动过程中,叶片落在扇形AOB内部的面积为_______cm2.
8.如图,P是正△ABC内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与P′之间的距离为PP′=_____,∠APB=______度.
9.如图,正方形ABCD中,E在BC上,△DEC按顺时针方向转动一个角度后成△DGA.
(1)图中哪一个点是旋转中心?
(2)旋转了多少度?
(3)已知CD=4,CE=3,求GE长.
23.1 图形的旋转
1.D
2.A解析:根据旋转的性质和旋转的方向得:△ABC绕O点按逆时针旋转90°后的图案是A,故选A.
3.B 解析:∵在Rt△ABC中,∠BAC=90°,将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处,∴AB1=BC,BB1=B1C,AB=AB1,∴BB1=AB=AB1,∴△ABB1是等边三角形,∴∠BAB1=60°,∴旋转的角度等于60°.
4.C 解析:连接AC、BD,AC与BD的交点即为旋转中心O.根据旋转的性质知,点C与点D对应,则∠DOC就是旋转角.∵四边形ABCD是正方形.∴∠DOC=90°.
5.D解析A、可由一个基本“花瓣”绕其中心经过7次旋转,每次旋转45°得到;
B、可由一个基本“菱形”绕其中心经过5次旋转,每次旋转60°得到;
C、可由一个基本图形绕其中心旋转180°得到;
D、不能由基本图案旋转得到.故选D.
.40 解析:∵∠1=∠2=∠3=20°,∴∠1+∠2=40°=∠BAD,即旋转角是40度.
7.24 解析:由图可知叶片落在扇形AOB内部的面积是图形面积的,因而叶片落在扇形AOB内部的面积为72×=24cm2.
8.6,150 解析:连接PP′,∵PA=6,PB=8,PC=P′B=10,∵∠PAP′=60°,∴P′A=PP′=PA=6,∴P′B=PC=10,∴∠P′PB=90°,∴∠APB=90°+60°=150°.
9.解:(1)旋转中心是点D;(2)∵△DEC按顺时针方向转动一个角度后成△DGA,∴旋转角的度数等于∠ADC的度数,∵四边形ABCD是正方形,∴∠ADC=90°,∴旋转了90°;
(3)∵四边形ABCD是正方形,∴∠B=90°,DC=AB=BC=4,∵CE=3,∴BE=4-3=1,∵△DEC按顺时针方向转动一个角度后成△DGA,∴△DEC≌△DGA,∴AG=CE=3,∴BG=3+4=7,在Rt△GBE中,GE===5.
同课章节目录
