人教版数学7年级下册 5.1相交线学案(含答案)
文档属性
| 名称 | 人教版数学7年级下册 5.1相交线学案(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 299.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-23 00:00:00 | ||
图片预览


文档简介
相交线
班级:_____________姓名:__________________组号:_________
拓展课
一、巩固训练
1.下面各图中∠1和∠2是对顶角的是( )
A B C D
2.如图,直线AB和CD相交于点O,若∠AOC=125°,则∠AOD=
( )
A.50° B.55° C.60° D.65°
3.如图,三条直线相交于点O。若CO⊥AB,∠1=56°,则∠2等于
( )
A.30° B.34° C.45° D.56°
4.如图,直线AB、CD相交于点O,若∠BOD=40°,OA平分∠COE,则∠AOE= 。
二、错题再现
1.∠1的对顶角是∠2,∠2的邻补角是∠3,若∠3=45 ,则∠1的度数是( )
A.45 B.135 C.45 和135 D.90
2.如图,直线AB、CD相交于点O,∠COE=90°,∠AOC=30°,∠FOB=90°,则∠EOF=________。
3.如图,AC⊥BC,CD⊥AB于D,AC=5cm,BC=12cm,AB=13cm,则点B到AC的距离是____________,点A到BC的距离是_______,点C到AB的距离是________________,AC>CD的依据是________________________。
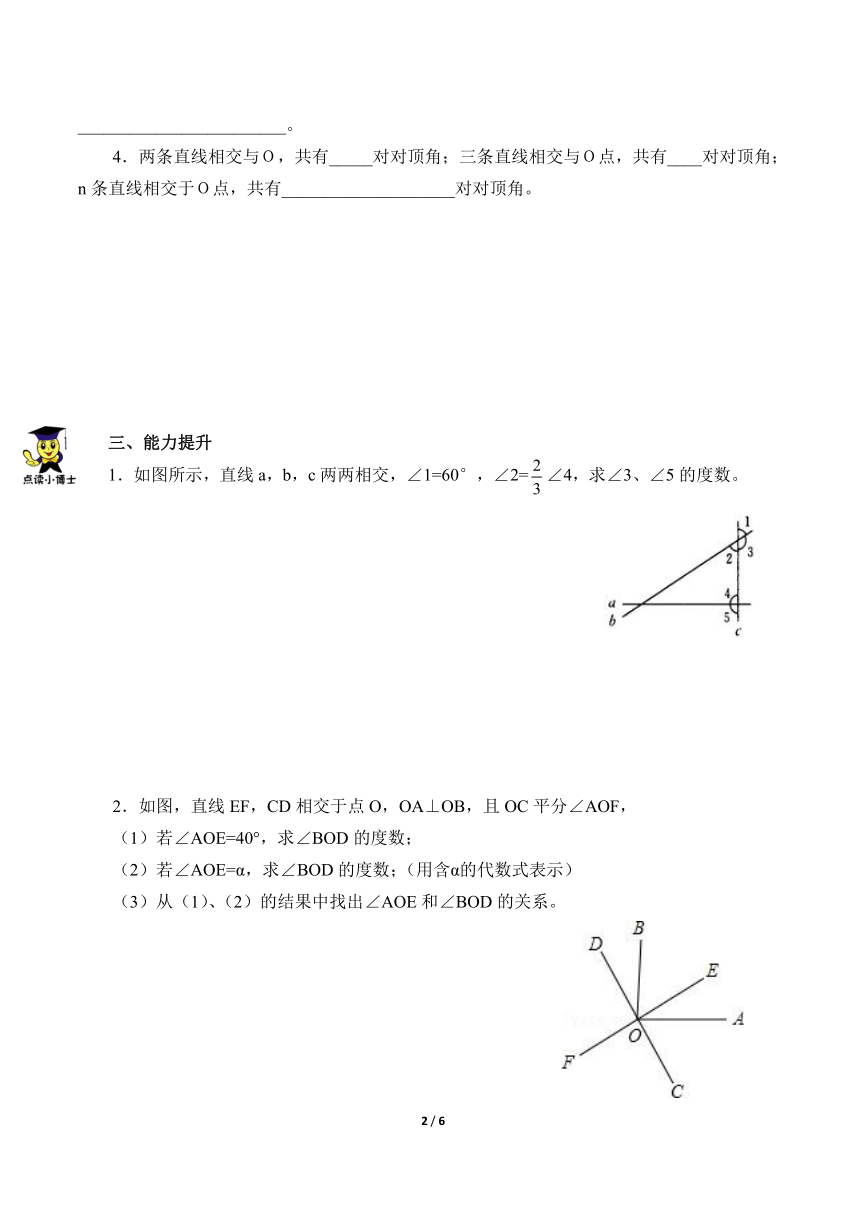
4.两条直线相交与O,共有_____对对顶角;三条直线相交与O点,共有____对对顶角;n条直线相交于O点,共有____________________对对顶角。
三、能力提升
1.如图所示,直线a,b,c两两相交,∠1=60°,∠2=∠4,求∠3、∠5的度数。
2.如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)、(2)的结果中找出∠AOE和∠BOD的关系。
四、精练反馈
A组:
1.如图,直线AB与直线CD相交于点O,E是平面内一点。若OE⊥AB,,则的度数是( )
A. B. C. D.
2.如图,直线AB、CD、EF相交于点O,∠BOE的对顶角是________,∠COF的邻补角是____________,若∠AOE=30°,那么∠BOE=__________,∠BOF=__________。
3.如图,AB是一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠DOE=∠BOD
∠COE=72°,则∠EOB=( )
A.36° B.72° C.108° D.120°
B组:
4.如图,AOB为直线,∠AOD:∠DOB=3:1,OD平分∠COB。
(1)求∠AOC的度数;
(2)判断AB与OC的位置关系。
【答案】
【巩固训练】
1.B
2.B
3.B
4.40°
【错题再现】
1.B
2.150°
3.12cm 5cm cm 垂线段最短
4.2 6 n(n+1)
【能力提升】
1.
2.(1)
(2)
(3)
【精练反馈】
1.B
2.∠AOF ∠DOF或∠COE 150° 30°
3.B
4.
完成情况
第2题
A
C
B
E
D
O
第1题图
第2题
第3题
6 / 6
班级:_____________姓名:__________________组号:_________
拓展课
一、巩固训练
1.下面各图中∠1和∠2是对顶角的是( )
A B C D
2.如图,直线AB和CD相交于点O,若∠AOC=125°,则∠AOD=
( )
A.50° B.55° C.60° D.65°
3.如图,三条直线相交于点O。若CO⊥AB,∠1=56°,则∠2等于
( )
A.30° B.34° C.45° D.56°
4.如图,直线AB、CD相交于点O,若∠BOD=40°,OA平分∠COE,则∠AOE= 。
二、错题再现
1.∠1的对顶角是∠2,∠2的邻补角是∠3,若∠3=45 ,则∠1的度数是( )
A.45 B.135 C.45 和135 D.90
2.如图,直线AB、CD相交于点O,∠COE=90°,∠AOC=30°,∠FOB=90°,则∠EOF=________。
3.如图,AC⊥BC,CD⊥AB于D,AC=5cm,BC=12cm,AB=13cm,则点B到AC的距离是____________,点A到BC的距离是_______,点C到AB的距离是________________,AC>CD的依据是________________________。
4.两条直线相交与O,共有_____对对顶角;三条直线相交与O点,共有____对对顶角;n条直线相交于O点,共有____________________对对顶角。
三、能力提升
1.如图所示,直线a,b,c两两相交,∠1=60°,∠2=∠4,求∠3、∠5的度数。
2.如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)、(2)的结果中找出∠AOE和∠BOD的关系。
四、精练反馈
A组:
1.如图,直线AB与直线CD相交于点O,E是平面内一点。若OE⊥AB,,则的度数是( )
A. B. C. D.
2.如图,直线AB、CD、EF相交于点O,∠BOE的对顶角是________,∠COF的邻补角是____________,若∠AOE=30°,那么∠BOE=__________,∠BOF=__________。
3.如图,AB是一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠DOE=∠BOD
∠COE=72°,则∠EOB=( )
A.36° B.72° C.108° D.120°
B组:
4.如图,AOB为直线,∠AOD:∠DOB=3:1,OD平分∠COB。
(1)求∠AOC的度数;
(2)判断AB与OC的位置关系。
【答案】
【巩固训练】
1.B
2.B
3.B
4.40°
【错题再现】
1.B
2.150°
3.12cm 5cm cm 垂线段最短
4.2 6 n(n+1)
【能力提升】
1.
2.(1)
(2)
(3)
【精练反馈】
1.B
2.∠AOF ∠DOF或∠COE 150° 30°
3.B
4.
完成情况
第2题
A
C
B
E
D
O
第1题图
第2题
第3题
6 / 6
