福建省厦门市湖里实验中学2023-2024学年九年级上学期数学第8周 周末练习(无答案)
文档属性
| 名称 | 福建省厦门市湖里实验中学2023-2024学年九年级上学期数学第8周 周末练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 242.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-23 13:19:49 | ||
图片预览

文档简介
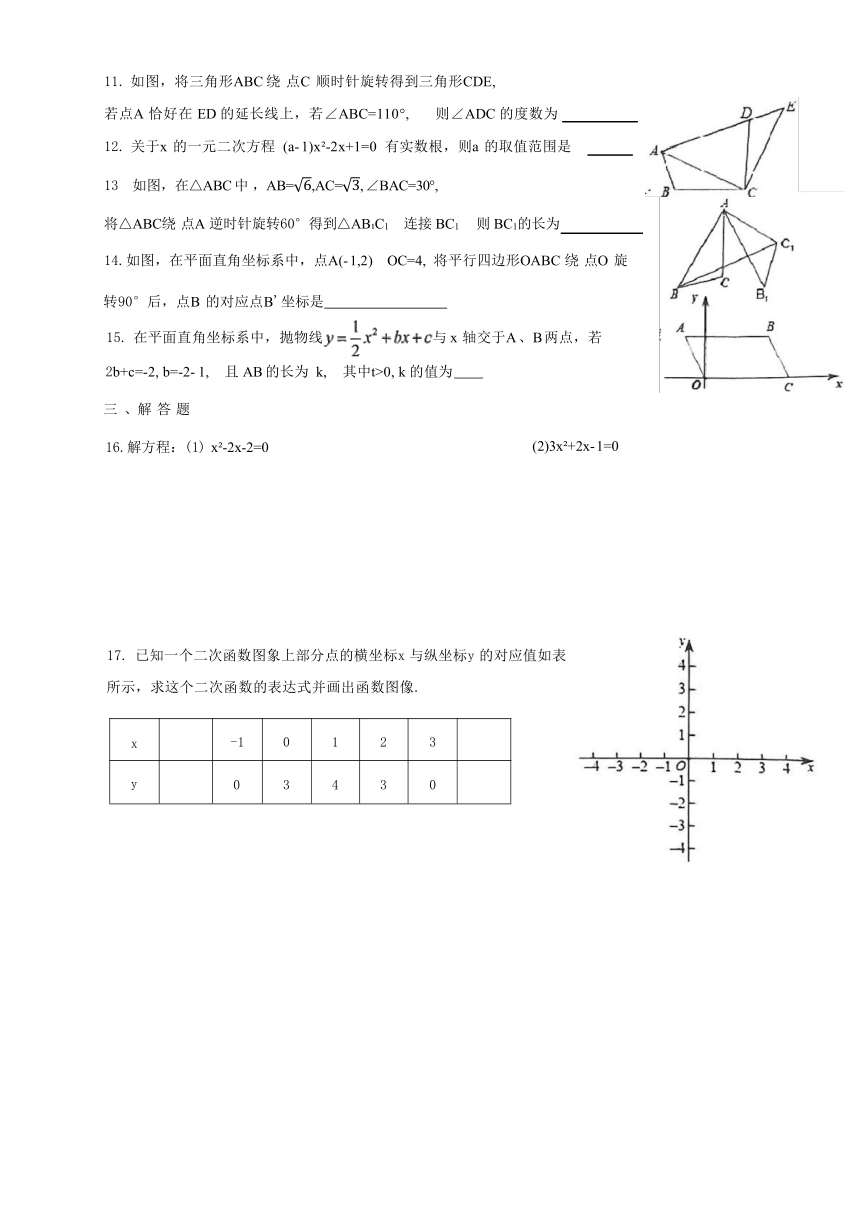
2023- 2024 学年厦门市湖里实验中学九上数学第 8 周周末练习 ( 1 0 . 2 1 )
班 级 姓 名 座 号
一、选择题
1. 下列图形中,是中心对称图形的是( )
A. B. C. D.
2.若将抛物线y=2x +3 向右平移3个单位,再向上平移2个单位,则所得抛物线解析式为( )
A y=(x+3) +5 B.y=2(x-3) - 1 C.y=2(x+3) - 1 D.y=2(x-3) +5
3. 如图,将该图形绕着它的中心旋转,要使其与自身重合,至少应旋转( )
A. 180° B.120 C.90° D.60°
4. 如图,将△AOB绕点O 按逆时针方向旋转45°后得到△A'OB', 若∠AOB=15°,
则∠AOB的度数是( )
A. 25° B. 30° C. 35° D. 40°
5. 下列说法正确的是( )
A. 平行四边形既是轴对称图形又是中心对称图形 B. 三个角是直角的四边形是矩形
C. 菱形的对角线相等且互相平分D. 对角线垂直平分的四边形是正方形
6.若抛物线y= -2 (x+m - 1) -3m + 6 的顶点在第二象限,则 m 的取值范围是( )
A. m>1 B.m<2 C. 17.如图,在平面直角坐标系xOy 中,△A'B'C '由△ABC 绕点P 旋转得到,则点P 的
(
坐标为(
)
A.(0,
1)
B.
(1,
-1)
C.
(0,
-1)
D.
(1,
0)
)
8. 如图,在Rt△ABC 中,∠C=90°,AC=BC,AB=8, 点D 为AB 的中点,若直角 MDN 绕点D 旋转分别交AC 于点E, 交 BC 于点F, 则下列说法:①AE=CF;
②EC+CF=4;③DE=DF;④若△ECF 的面积为一个定值,则EF 的长也是一个
定值,其中正确的是( )
A.①② B.①③ C.①②③ D.①②③④
二、 填空题
9. 抛物线y=2x -3 与y 轴交点的坐标是
10.已知x=1 是方程x -ax+7=0 的一个根,则a 的值是
11. 如图,将三角形ABC 绕 点C 顺时针旋转得到三角形CDE,
若点A 恰好在 ED 的延长线上,若∠ABC=110°, 则∠ADC 的度数为
12. 关于x 的一元二次方程 (a- 1)x -2x+1=0 有实数根,则a 的取值范围是
13 如图,在△ABC 中 ,AB=,AC=, ∠BAC=30°,
将△ABC绕 点A 逆时针旋转60°得到△AB C1 连接 BC1 则 BC1的长为
14.如图,在平面直角坐标系中,点A(- 1,2) OC=4, 将平行四边形OABC 绕 点O 旋
转90°后,点B 的对应点B'坐标是
15. 在平面直角坐标系中,抛物线与 x 轴交于A 、B 两点,若2b+c=-2, b=-2- 1, 且 AB 的长为 k, 其中t>0, k 的值为
三 、解 答 题
16.解方程:(1) x -2x-2=0 (2)3x +2x- 1=0
17. 已知一个二次函数图象上部分点的横坐标x 与纵坐标y 的对应值如表
所示,求这个二次函数的表达式并画出函数图像.
x -1 0 1 2 3
y 0 3 4 3 0
18.先化简,再求值:
, 其 中a= √2-1.
19. 如图,△ABC中,∠C=90° .
(1)将△ABC 绕 点B 逆时针旋转90°,画出旋转后的△A BC ;
( 2 ) 若BC=3,AC=4, 点A 旋转后的对应点A, 求 AA 的长.
20. 如图,在四边形ABCD 中 ,BC=CD, ∠BCD=a°, ∠ABC+ ∠ADC=180°,AC 、BD 交于点 E. 将△CBA
绕点 C 顺时针旋转a °得到△CDF.
(1)求证:∠CAB= ∠CAD;
(2)若∠ABD=90°,AB=3,BD=4,△BCE
的面积为Si,△CDE 的面积为S , 求S:S 的值。
(
.
.
) (
.
)21 根据以下素材,探索完成任务
如何设计打印图纸方案
素 材 1 如图1,正方形ABCD是一张用于 3D打印产品的示意图,它由三个 区块(I,Ⅱ,Ⅲ)构成 . 已知 AB=10cm,点E,F分别在BC和 AB上,且BE=BE,设BE=x cm (0素 材 2 为了打印精准,拟在图2中的BC 边上设置一排间距为1cm的定位 坐标(B为坐标原点),计算机可 根据点E的定位坐标精准打印出 图案 . A F B D E C 图2
问题解决
(
1
)任务 确定关系 用x的代数式表示: 区域I的面积 = ; 区 域 Ⅱ 的 面积= .
(
2
)任务 拟定方案 为了美观,拟将区域Ⅲ分割为甲、乙两 个三角形区域,并要求区域乙是含DE 边的三角形,求所有方案中乙的面积或 者函数表达式.
(
3
)任务 优化设计 经调查发现当2.5≤x≤6.5且x为整数 时,此时称E点为合格定位点.当区域 乙的面积最小时,合格定位点E点为最 佳定位点,求出最佳定位点E的坐标
班 级 姓 名 座 号
一、选择题
1. 下列图形中,是中心对称图形的是( )
A. B. C. D.
2.若将抛物线y=2x +3 向右平移3个单位,再向上平移2个单位,则所得抛物线解析式为( )
A y=(x+3) +5 B.y=2(x-3) - 1 C.y=2(x+3) - 1 D.y=2(x-3) +5
3. 如图,将该图形绕着它的中心旋转,要使其与自身重合,至少应旋转( )
A. 180° B.120 C.90° D.60°
4. 如图,将△AOB绕点O 按逆时针方向旋转45°后得到△A'OB', 若∠AOB=15°,
则∠AOB的度数是( )
A. 25° B. 30° C. 35° D. 40°
5. 下列说法正确的是( )
A. 平行四边形既是轴对称图形又是中心对称图形 B. 三个角是直角的四边形是矩形
C. 菱形的对角线相等且互相平分D. 对角线垂直平分的四边形是正方形
6.若抛物线y= -2 (x+m - 1) -3m + 6 的顶点在第二象限,则 m 的取值范围是( )
A. m>1 B.m<2 C. 1
(
坐标为(
)
A.(0,
1)
B.
(1,
-1)
C.
(0,
-1)
D.
(1,
0)
)
8. 如图,在Rt△ABC 中,∠C=90°,AC=BC,AB=8, 点D 为AB 的中点,若直角 MDN 绕点D 旋转分别交AC 于点E, 交 BC 于点F, 则下列说法:①AE=CF;
②EC+CF=4;③DE=DF;④若△ECF 的面积为一个定值,则EF 的长也是一个
定值,其中正确的是( )
A.①② B.①③ C.①②③ D.①②③④
二、 填空题
9. 抛物线y=2x -3 与y 轴交点的坐标是
10.已知x=1 是方程x -ax+7=0 的一个根,则a 的值是
11. 如图,将三角形ABC 绕 点C 顺时针旋转得到三角形CDE,
若点A 恰好在 ED 的延长线上,若∠ABC=110°, 则∠ADC 的度数为
12. 关于x 的一元二次方程 (a- 1)x -2x+1=0 有实数根,则a 的取值范围是
13 如图,在△ABC 中 ,AB=,AC=, ∠BAC=30°,
将△ABC绕 点A 逆时针旋转60°得到△AB C1 连接 BC1 则 BC1的长为
14.如图,在平面直角坐标系中,点A(- 1,2) OC=4, 将平行四边形OABC 绕 点O 旋
转90°后,点B 的对应点B'坐标是
15. 在平面直角坐标系中,抛物线与 x 轴交于A 、B 两点,若2b+c=-2, b=-2- 1, 且 AB 的长为 k, 其中t>0, k 的值为
三 、解 答 题
16.解方程:(1) x -2x-2=0 (2)3x +2x- 1=0
17. 已知一个二次函数图象上部分点的横坐标x 与纵坐标y 的对应值如表
所示,求这个二次函数的表达式并画出函数图像.
x -1 0 1 2 3
y 0 3 4 3 0
18.先化简,再求值:
, 其 中a= √2-1.
19. 如图,△ABC中,∠C=90° .
(1)将△ABC 绕 点B 逆时针旋转90°,画出旋转后的△A BC ;
( 2 ) 若BC=3,AC=4, 点A 旋转后的对应点A, 求 AA 的长.
20. 如图,在四边形ABCD 中 ,BC=CD, ∠BCD=a°, ∠ABC+ ∠ADC=180°,AC 、BD 交于点 E. 将△CBA
绕点 C 顺时针旋转a °得到△CDF.
(1)求证:∠CAB= ∠CAD;
(2)若∠ABD=90°,AB=3,BD=4,△BCE
的面积为Si,△CDE 的面积为S , 求S:S 的值。
(
.
.
) (
.
)21 根据以下素材,探索完成任务
如何设计打印图纸方案
素 材 1 如图1,正方形ABCD是一张用于 3D打印产品的示意图,它由三个 区块(I,Ⅱ,Ⅲ)构成 . 已知 AB=10cm,点E,F分别在BC和 AB上,且BE=BE,设BE=x cm (0
问题解决
(
1
)任务 确定关系 用x的代数式表示: 区域I的面积 = ; 区 域 Ⅱ 的 面积= .
(
2
)任务 拟定方案 为了美观,拟将区域Ⅲ分割为甲、乙两 个三角形区域,并要求区域乙是含DE 边的三角形,求所有方案中乙的面积或 者函数表达式.
(
3
)任务 优化设计 经调查发现当2.5≤x≤6.5且x为整数 时,此时称E点为合格定位点.当区域 乙的面积最小时,合格定位点E点为最 佳定位点,求出最佳定位点E的坐标
