2023-2024学年第一学期九年级数学第22章二次函数单元测试卷(含答案)
文档属性
| 名称 | 2023-2024学年第一学期九年级数学第22章二次函数单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 172.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-23 12:54:56 | ||
图片预览



文档简介
2023-2024学年第一学期九年级数学第22章二次函数单元测试卷人教版
一、选择题(每小题3分,共30分)
1.下列函数是二次函数的是( )
A. B. C. D.
2.将抛物线y=x2+3先向左平移2个单位,再向下平移1个单位,所得新抛物线的解析式为( )
A.y=(x+2)2+2 B.y=(x﹣1)2+5
C.y=(x+2)2+4 D.y=(x﹣2)2+2
3.已知抛物线y=ax2+bx+c的开口向下,顶点坐标为(2,-3),那么该抛物线有( )
A.最小值-3 B.最大值-3 C.最小值2 D.最大值2
4.抛物线的顶点坐标是( )
A. B. C. D.
5.若二次函数y=ax2的图象经过点P(﹣2,4),则该图象必经过点( )
A.(4,﹣2) B.(﹣4,2)
C.(﹣2,﹣4) D.(2,4)
6. 的对称轴是直线( )
A.x=-1 B.x=1 C.y=-1 D.y=1
7.如图所示,当时,函数与函数的图象大致是( ).
A. B.
C. D.
8.用配方法将二次函数化为的形式为( ).
A. B.
C. D.
9.抛物线y=2(x﹣1)2+c上有点A(﹣1,y1)和B(4,y2),则y1与y2的大小关系为( )
A.y1≤y2 B.y1≥y2 C.y1<y2 D.y1>y2
10.如图所示,二次函数的图象与轴交于A,B两点,与轴正半轴交于点,它的对称轴为直线.下列选项中,正确的是( ).
A. B.
C. D.当(为实数)时,
二、填空题(每小题3分,共24分)
11.如果点A(﹣3,y1)和点B(﹣2,y2)是抛物线y=x2+a上的两点,那么y1 y2.(填“>”、“=”、“<”).
12.二次函数 图象的顶点是 .
13.二次函数 的最大值是 .
14.将抛物线y=x2+2x+3向左平移1个单位,再向下平移2个单位,平移后的抛物线解析式为 .
15.若二次函数的 的图象经过点 ,则 .
16.某超市一月份的营业额是200万元,一月、二月、三月的营业额共万元,如果平均每月增长率为,那么营业额关于月平均增长率的函数表达式为 .
17.函数的图象与轴有且只有一个交点,则的值为 .
18.已知抛物线与x轴的一个交点为,则代数式的值为 .
四、作图题(共9分)
19.已知二次函数经过点,,且最大值为.
(1)求二次函数的解析式;
(2)在平面直角坐标系中,画出二次函数的图象;
(3)当时,结合函数图象,直接写出的取值范围.
五、解答题(一)(共35分)
20.(6分)按要求求出抛物线的开口方向、对称轴和顶点坐标.
(1)(用配方法). (2)(用公式法).
21.(6分)已知抛物线的顶点是 A(2,﹣3),且交 y 轴于点 B(0,5),求此抛物线的解析式.
22.(9分)丹东是我国的边境城市,拥有丰富的旅游资源.某景区研发一款纪念品,每件成本为30元,投放景区内进行销售,规定销售单价不低于成本且不高于54元,销售一段时间调研发现,每天的销售数量y(件)与销售单价x(元/件)满足一次函数关系,部分数据如下表所示:
销售单价x(元/件) … 35 40 45 …
每天销售数量y(件) … 90 80 70 …
(1)直接写出y与x的函数关系式;
(2)若每天销售所得利润为1200元,那么销售单价应定为多少元?
(3)当销售单价为多少元时,每天获利最大?最大利润是多少元?
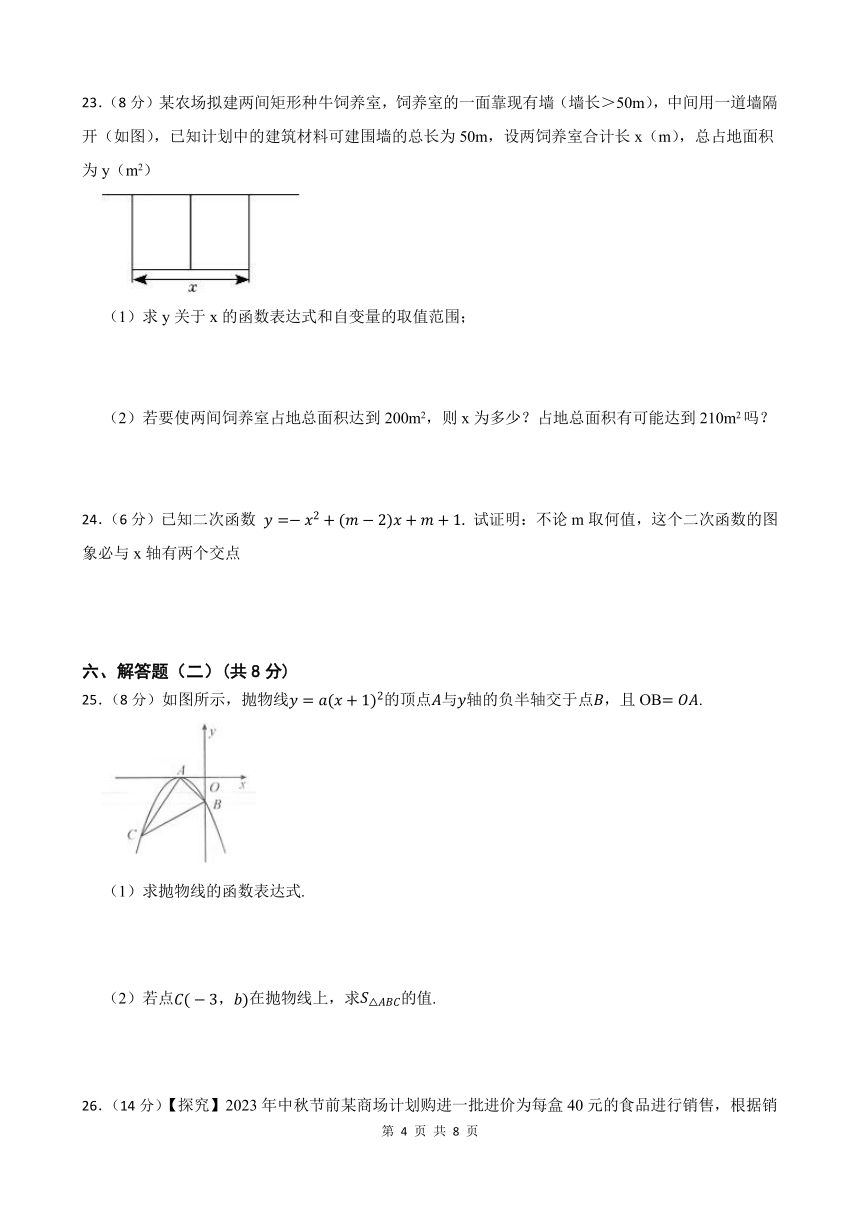
23.(8分)某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长>50m),中间用一道墙隔开(如图),已知计划中的建筑材料可建围墙的总长为50m,设两饲养室合计长x(m),总占地面积为y(m2)
(1)求y关于x的函数表达式和自变量的取值范围;
(2)若要使两间饲养室占地总面积达到200m2,则x为多少?占地总面积有可能达到210m2吗?
24.(6分)已知二次函数 试证明:不论m取何值,这个二次函数的图象必与x轴有两个交点
六、解答题(二)(共8分)
25.(8分)如图所示,抛物线的顶点与轴的负半轴交于点,且OB.
(1)求抛物线的函数表达式.
(2)若点在抛物线上,求的值.
26.(14分)【探究】2023年中秋节前某商场计划购进一批进价为每盒40元的食品进行销售,根据销售经验,应季销售时,若每盒食品的售价为60元,则可售出400盒,当每盒食品的售价每提高1元,销售量就相应减少10盒.
(1)(4分)假设每盒食品的售价提高x元,那么销售每盒食品所获得的利润是 元,销售量是 盒.(用含x为代数式表示)
(2)(3分)设应季销售利润为y元,求y与x的函数关系式,并求出应季销售利润为8000元时每盒食品的售价.
(3)【拓展】根据销售经验,过季处理时,若每盒食品的售价定为30元亏本销售,可售出50盒,若每盒食品的售价每降低1元,销售量就相应增加5盒.当单价降低z元时,解答:
现剩余100盒食品需要处理,经过降价处理后还是无法销售的只能积压在仓库,损失本金,若使亏损金额最小,此时每盒食品的售价应为 元;
(4)(4分)若过季需要处理的食品共m盒,过季处理时亏损金额为y1元,求y1与z的函数关系式;当100≤m≤300时,求过季销售亏损金额最小时多少元?
答案
1.C 2.A 3.B 4.B 5.D 6.B 7.C 8.B 9.C 10.D
11.> 12.(3,-2) 13.7 14.y=(x+2)2 15. 16.
17.-2或2或3 18.2019
19.(1)解:设抛物线解析式为,
由最大值为,得到,即,
则抛物线解析式为
(2)解:列表:
描点、连线,
函数图象如图所示;
;
(3)解:
20.(1),
抛物线的开口向上,对称轴为直线,顶点坐标为
(2),
拋物线的开口向上,对称轴为直线,顶点坐标为
21.解:∵抛物线的顶点坐标为 A(2,﹣3),
∴可设抛物线解析式为 y=a(x﹣2)2﹣3, 将 B(0,5)代入,得 4a﹣3=5,
解得 a=2,
∴抛物线的解析式为 y=2(x﹣2)2﹣3 化为一般式为
y=2x2﹣8x+5
22.(1)y=﹣2x+160
(2)解:根据题意得:(x﹣30) (﹣2x+160)=1200,
解得x1=50,x2=60,
∵规定销售单价不低于成本且不高于54元,
∴x=50,
答:销售单价应定为50元;
(3)解:设每天获利w元,
w=(x﹣30) (﹣2x+160)=﹣2x2+220x﹣4800=﹣2(x﹣55)2+1250,
∵﹣2<0,对称轴是直线x=55,
而x≤54,
∴x=54时,w取最大值,最大值是﹣2×(54﹣55)2+1250=1248(元),
答:当销售单价为54元时,每天获利最大,最大利润,1248元.
23.(1)解:∵围墙的总长为50米,2间饲养室合计长x米,
∴饲养室的宽=米,
∴总占地面积为y=x =﹣x2+x,(0<x<50);
(2)解:当两间饲养室占地总面积达到200平方米时,则﹣x2+x=200,
解得:x=20或30;
∴当面积达到200平方米时,各道墙长分别为20米、10米或30米、米;
当占地面积达到210平方米时,则﹣x2+x=210,
方程的Δ<0,所以此方程无解,
∴占地面积不可能达到210平方米.
24.证明:由题意,知二次函数对应的方程 的判别式为 .
因为 ,所以 ,即 ,
所以不论m取何值,这个二次函数的图象必与x轴有两个交点.
25.(1)解:∵
∴A(-1,0),
∵OA=OB,
∴B(1,0),
把B(1,0)代入中,得a=-1,
∴
(2)如图,过点C作CD⊥x轴,
把 代入 中,得b=-4,
∴C(-3,-4),
∴=梯形OBCD的面积-△ACD的面积-△OAB的面积
=×(1+4)×3-×2×4-×1×1=3,
26.(1)20+x;400﹣10x
(2)解:根据题意得:y=(20+x)(400﹣10x)=﹣10x2+200x+8000,
把y=8000代入,得:﹣10x2+200x+8000=8000,
解得:x=0或x=20,
当x=0时,60+x=60,
当x=20时,60+x=80,
答:应季销售利润为8000元时每盒食品的售价为60元或80元
(3)20
(4)解:y1=40m﹣(30﹣z)(50+5z)=5(z﹣10)2+40m﹣2000,
即当z=10时,y1有最小值40m﹣2000,
∵100≤m≤300,
∴当m=100时,y1有最小值40m﹣2000=2000,
答:过季销售亏损金额最小时2000元
一、选择题(每小题3分,共30分)
1.下列函数是二次函数的是( )
A. B. C. D.
2.将抛物线y=x2+3先向左平移2个单位,再向下平移1个单位,所得新抛物线的解析式为( )
A.y=(x+2)2+2 B.y=(x﹣1)2+5
C.y=(x+2)2+4 D.y=(x﹣2)2+2
3.已知抛物线y=ax2+bx+c的开口向下,顶点坐标为(2,-3),那么该抛物线有( )
A.最小值-3 B.最大值-3 C.最小值2 D.最大值2
4.抛物线的顶点坐标是( )
A. B. C. D.
5.若二次函数y=ax2的图象经过点P(﹣2,4),则该图象必经过点( )
A.(4,﹣2) B.(﹣4,2)
C.(﹣2,﹣4) D.(2,4)
6. 的对称轴是直线( )
A.x=-1 B.x=1 C.y=-1 D.y=1
7.如图所示,当时,函数与函数的图象大致是( ).
A. B.
C. D.
8.用配方法将二次函数化为的形式为( ).
A. B.
C. D.
9.抛物线y=2(x﹣1)2+c上有点A(﹣1,y1)和B(4,y2),则y1与y2的大小关系为( )
A.y1≤y2 B.y1≥y2 C.y1<y2 D.y1>y2
10.如图所示,二次函数的图象与轴交于A,B两点,与轴正半轴交于点,它的对称轴为直线.下列选项中,正确的是( ).
A. B.
C. D.当(为实数)时,
二、填空题(每小题3分,共24分)
11.如果点A(﹣3,y1)和点B(﹣2,y2)是抛物线y=x2+a上的两点,那么y1 y2.(填“>”、“=”、“<”).
12.二次函数 图象的顶点是 .
13.二次函数 的最大值是 .
14.将抛物线y=x2+2x+3向左平移1个单位,再向下平移2个单位,平移后的抛物线解析式为 .
15.若二次函数的 的图象经过点 ,则 .
16.某超市一月份的营业额是200万元,一月、二月、三月的营业额共万元,如果平均每月增长率为,那么营业额关于月平均增长率的函数表达式为 .
17.函数的图象与轴有且只有一个交点,则的值为 .
18.已知抛物线与x轴的一个交点为,则代数式的值为 .
四、作图题(共9分)
19.已知二次函数经过点,,且最大值为.
(1)求二次函数的解析式;
(2)在平面直角坐标系中,画出二次函数的图象;
(3)当时,结合函数图象,直接写出的取值范围.
五、解答题(一)(共35分)
20.(6分)按要求求出抛物线的开口方向、对称轴和顶点坐标.
(1)(用配方法). (2)(用公式法).
21.(6分)已知抛物线的顶点是 A(2,﹣3),且交 y 轴于点 B(0,5),求此抛物线的解析式.
22.(9分)丹东是我国的边境城市,拥有丰富的旅游资源.某景区研发一款纪念品,每件成本为30元,投放景区内进行销售,规定销售单价不低于成本且不高于54元,销售一段时间调研发现,每天的销售数量y(件)与销售单价x(元/件)满足一次函数关系,部分数据如下表所示:
销售单价x(元/件) … 35 40 45 …
每天销售数量y(件) … 90 80 70 …
(1)直接写出y与x的函数关系式;
(2)若每天销售所得利润为1200元,那么销售单价应定为多少元?
(3)当销售单价为多少元时,每天获利最大?最大利润是多少元?
23.(8分)某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长>50m),中间用一道墙隔开(如图),已知计划中的建筑材料可建围墙的总长为50m,设两饲养室合计长x(m),总占地面积为y(m2)
(1)求y关于x的函数表达式和自变量的取值范围;
(2)若要使两间饲养室占地总面积达到200m2,则x为多少?占地总面积有可能达到210m2吗?
24.(6分)已知二次函数 试证明:不论m取何值,这个二次函数的图象必与x轴有两个交点
六、解答题(二)(共8分)
25.(8分)如图所示,抛物线的顶点与轴的负半轴交于点,且OB.
(1)求抛物线的函数表达式.
(2)若点在抛物线上,求的值.
26.(14分)【探究】2023年中秋节前某商场计划购进一批进价为每盒40元的食品进行销售,根据销售经验,应季销售时,若每盒食品的售价为60元,则可售出400盒,当每盒食品的售价每提高1元,销售量就相应减少10盒.
(1)(4分)假设每盒食品的售价提高x元,那么销售每盒食品所获得的利润是 元,销售量是 盒.(用含x为代数式表示)
(2)(3分)设应季销售利润为y元,求y与x的函数关系式,并求出应季销售利润为8000元时每盒食品的售价.
(3)【拓展】根据销售经验,过季处理时,若每盒食品的售价定为30元亏本销售,可售出50盒,若每盒食品的售价每降低1元,销售量就相应增加5盒.当单价降低z元时,解答:
现剩余100盒食品需要处理,经过降价处理后还是无法销售的只能积压在仓库,损失本金,若使亏损金额最小,此时每盒食品的售价应为 元;
(4)(4分)若过季需要处理的食品共m盒,过季处理时亏损金额为y1元,求y1与z的函数关系式;当100≤m≤300时,求过季销售亏损金额最小时多少元?
答案
1.C 2.A 3.B 4.B 5.D 6.B 7.C 8.B 9.C 10.D
11.> 12.(3,-2) 13.7 14.y=(x+2)2 15. 16.
17.-2或2或3 18.2019
19.(1)解:设抛物线解析式为,
由最大值为,得到,即,
则抛物线解析式为
(2)解:列表:
描点、连线,
函数图象如图所示;
;
(3)解:
20.(1),
抛物线的开口向上,对称轴为直线,顶点坐标为
(2),
拋物线的开口向上,对称轴为直线,顶点坐标为
21.解:∵抛物线的顶点坐标为 A(2,﹣3),
∴可设抛物线解析式为 y=a(x﹣2)2﹣3, 将 B(0,5)代入,得 4a﹣3=5,
解得 a=2,
∴抛物线的解析式为 y=2(x﹣2)2﹣3 化为一般式为
y=2x2﹣8x+5
22.(1)y=﹣2x+160
(2)解:根据题意得:(x﹣30) (﹣2x+160)=1200,
解得x1=50,x2=60,
∵规定销售单价不低于成本且不高于54元,
∴x=50,
答:销售单价应定为50元;
(3)解:设每天获利w元,
w=(x﹣30) (﹣2x+160)=﹣2x2+220x﹣4800=﹣2(x﹣55)2+1250,
∵﹣2<0,对称轴是直线x=55,
而x≤54,
∴x=54时,w取最大值,最大值是﹣2×(54﹣55)2+1250=1248(元),
答:当销售单价为54元时,每天获利最大,最大利润,1248元.
23.(1)解:∵围墙的总长为50米,2间饲养室合计长x米,
∴饲养室的宽=米,
∴总占地面积为y=x =﹣x2+x,(0<x<50);
(2)解:当两间饲养室占地总面积达到200平方米时,则﹣x2+x=200,
解得:x=20或30;
∴当面积达到200平方米时,各道墙长分别为20米、10米或30米、米;
当占地面积达到210平方米时,则﹣x2+x=210,
方程的Δ<0,所以此方程无解,
∴占地面积不可能达到210平方米.
24.证明:由题意,知二次函数对应的方程 的判别式为 .
因为 ,所以 ,即 ,
所以不论m取何值,这个二次函数的图象必与x轴有两个交点.
25.(1)解:∵
∴A(-1,0),
∵OA=OB,
∴B(1,0),
把B(1,0)代入中,得a=-1,
∴
(2)如图,过点C作CD⊥x轴,
把 代入 中,得b=-4,
∴C(-3,-4),
∴=梯形OBCD的面积-△ACD的面积-△OAB的面积
=×(1+4)×3-×2×4-×1×1=3,
26.(1)20+x;400﹣10x
(2)解:根据题意得:y=(20+x)(400﹣10x)=﹣10x2+200x+8000,
把y=8000代入,得:﹣10x2+200x+8000=8000,
解得:x=0或x=20,
当x=0时,60+x=60,
当x=20时,60+x=80,
答:应季销售利润为8000元时每盒食品的售价为60元或80元
(3)20
(4)解:y1=40m﹣(30﹣z)(50+5z)=5(z﹣10)2+40m﹣2000,
即当z=10时,y1有最小值40m﹣2000,
∵100≤m≤300,
∴当m=100时,y1有最小值40m﹣2000=2000,
答:过季销售亏损金额最小时2000元
同课章节目录
