数学核心素养2023—2024学年苏科版数学八年级上册第三章 勾股定理小结与思考 学案(无答案)
文档属性
| 名称 | 数学核心素养2023—2024学年苏科版数学八年级上册第三章 勾股定理小结与思考 学案(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 243.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-23 15:05:38 | ||
图片预览

文档简介
2023年秋学期八年级数学学案
课题:第三章小结与思考 班级: 姓名: 学号:
〖自学自练展素养〗
【学习目标】
基础目标:能运用勾股定理及逆定理解决实际问题.
提高目标:感受数学的“转化”思想(把解斜三角形问题转化为解直角三角形的问题).
【知识梳理】
1.在Rt△ABC中,∠C=90°则直角边a,b,和斜边c 满足的关系式为 .
2. △ABC的边长分别为a,b,c,若a +b = c ,则它是 三角形,其中∠ =90°.
3.写出三组常见的勾股数 .
〖研学随练展收获〗
一.【基础练习】
1.填写下列图形中未知正方形的面积:
(
64
36
S
)
S =______ ;
( 第1题) ( 第2题)
2. 如图,△ABC中∠ACB=90°,
(1) 若∠B=30°,AC=4,则AB= ,中线 CD=
(2)若AC=5,BC=12,则AB= ,AB边上的高为 .
3.若三角形的三边为1.5、2、2.5、则此三角形为 三角形.
二.【问题探究】
问题1.(1)在Rt△ABC中,∠C=90°.
①若a=3,b=4,则c= ;
②若c=34,a:b=8:15,则 a= ,b= ;
(2)已知三角形的三边长为 9 ,12 ,15 ,则这个三角形的最大角是 度;
(3)若△ABC中 ,AB=5 ,BC=12 ,AC=13 ,则AC边上的高长为 ;
问题2.分类思想
(1)已知:直角三角形的三边长分别是3,4,X,则X2=
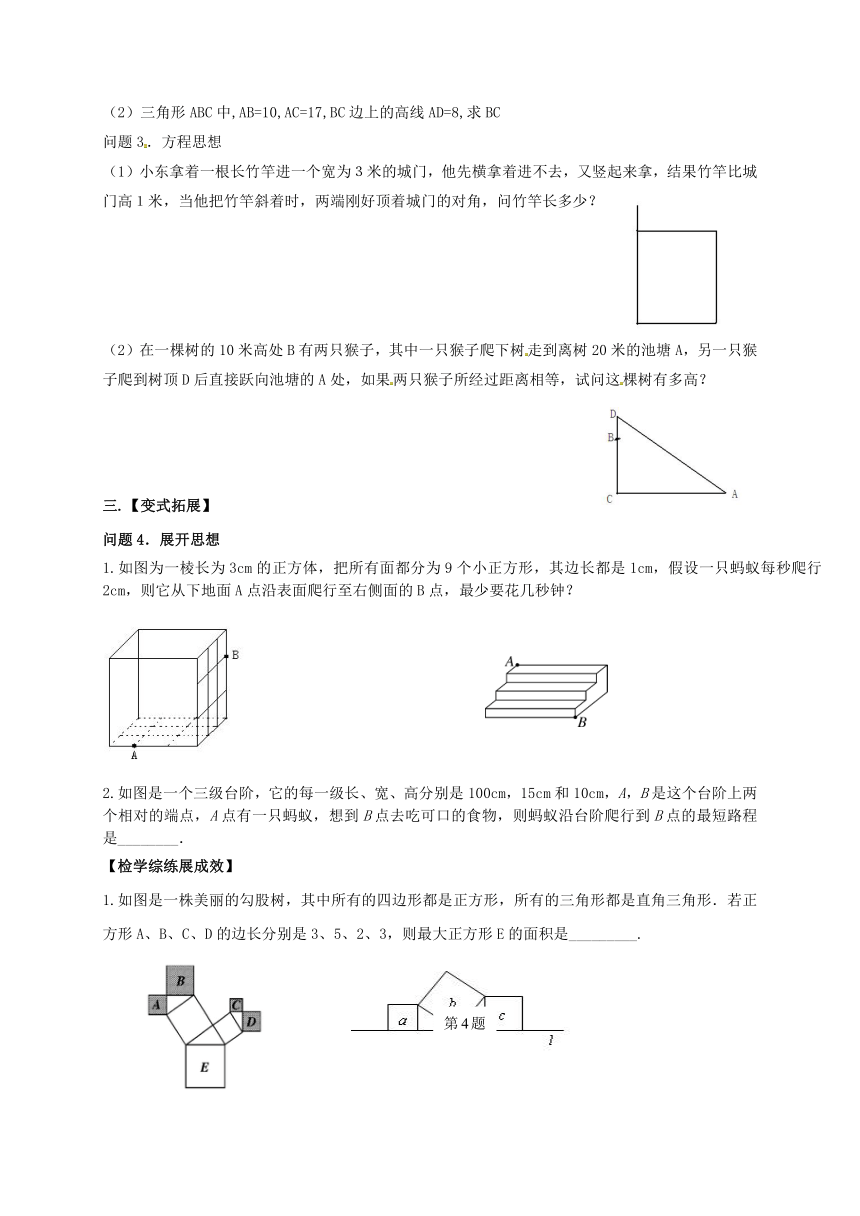
(2)三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC
问题3.方程思想
(1)小东拿着一根长竹竿进一个宽为3米的城门,他先横拿着进不去,又竖起来拿,结果竹竿比城门高1米,当他把竹竿斜着时,两端刚好顶着城门的对角,问竹竿长多少?
(2)在一棵树的10米高处B有两只猴子,其中一只猴子爬下树走到离树20米的池塘A,另一只猴子爬到树顶D后直接跃向池塘的A处,如果两只猴子所经过距离相等,试问这棵树有多高?
三.【变式拓展】
问题4.展开思想
1.如图为一棱长为3cm的正方体,把所有面都分为9个小正方形,其边长都是1cm,假设一只蚂蚁每秒爬行2cm,则它从下地面A点沿表面爬行至右侧面的B点,最少要花几秒钟?
2.如图是一个三级台阶,它的每一级长、宽、高分别是100cm,15cm和10cm,A,B是这个台阶上两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿台阶爬行到B点的最短路程是________.
【检学综练展成效】
1.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是_________.
(
第
4
题
)
三角形的三边长分别为 a2+b2、2ab、a2-b2(a、b都是正整数),则这个三角形是( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
如果把直角三角形的两条直角边同时扩大到原来的2倍,那么斜边扩大到原来的( )
A.1倍 B. 2倍 C. 3倍 D. 4倍
4.如图,直线上有三个正方形,若的面积分别为5和11,则的面积
= .
(
A
B
C
D
E
C
'
)5.将长方形ABCD沿直线BD折叠,使点C落在C'处,BC'交AD于E,AD=8,AB=4,
(1)△BED是 三角形,并说明理由.
(2)求△BED的面积.
6、如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
(1)判断∠D是否是直角,并说明理由.
(2)求四边形ABCD的面积.
7.如图,铁路A、B两站相距25km,C、D是两个工厂,位于铁路的同侧,其中,,且AC=15km,BD=10km
(1)尺规作图,在铁路AB上找一个点E建中转站,使得CE=DE,请作出这个点.
(
A
C
B
D
)(2)此时中转站E距A站多远
【校本作业】
一、必做题
1.在RtΔABC中,∠C=900(1)a=40,c=41,则b=______. (2)若a:c=6:10,c=20,则a=____,b=____ 2.若等腰三角形腰长为10cm,底边长为16 cm, 那么它的面积为 cm2.
3.若三角形的三边长a、b、c满足(a+b)2=c2+2ab,则这个三角形是( ).
(A)锐角三角形 (B)钝角三角形
(C)直角三角形 (D)何类三角形不能确定
4.“交通管理条例第三十五条”规定:小汽车在城街路上行驶速度不得超过千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方50米处,过了4秒后,测得小汽车与车速检测仪间距离为130米,这辆小汽车超速了吗?(提示:1米/秒=3.6千米/小时)
我国古代数学家赵爽用来证明勾股定理的弦图,可以说是充分肯定了我国数学的成就,也弘扬了我国古代的数学文化.弦图是由四个全等的直角三角形和中间的 小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么你能求出(a+b)2 的值吗?
二、选做题
6、如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.(1)求证:△ACE≌△BCD;(2)若AD=5,BD=12,求DE的长
三、拓展题
如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1) 观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2) 若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.
课题:第三章小结与思考 班级: 姓名: 学号:
〖自学自练展素养〗
【学习目标】
基础目标:能运用勾股定理及逆定理解决实际问题.
提高目标:感受数学的“转化”思想(把解斜三角形问题转化为解直角三角形的问题).
【知识梳理】
1.在Rt△ABC中,∠C=90°则直角边a,b,和斜边c 满足的关系式为 .
2. △ABC的边长分别为a,b,c,若a +b = c ,则它是 三角形,其中∠ =90°.
3.写出三组常见的勾股数 .
〖研学随练展收获〗
一.【基础练习】
1.填写下列图形中未知正方形的面积:
(
64
36
S
)
S =______ ;
( 第1题) ( 第2题)
2. 如图,△ABC中∠ACB=90°,
(1) 若∠B=30°,AC=4,则AB= ,中线 CD=
(2)若AC=5,BC=12,则AB= ,AB边上的高为 .
3.若三角形的三边为1.5、2、2.5、则此三角形为 三角形.
二.【问题探究】
问题1.(1)在Rt△ABC中,∠C=90°.
①若a=3,b=4,则c= ;
②若c=34,a:b=8:15,则 a= ,b= ;
(2)已知三角形的三边长为 9 ,12 ,15 ,则这个三角形的最大角是 度;
(3)若△ABC中 ,AB=5 ,BC=12 ,AC=13 ,则AC边上的高长为 ;
问题2.分类思想
(1)已知:直角三角形的三边长分别是3,4,X,则X2=
(2)三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC
问题3.方程思想
(1)小东拿着一根长竹竿进一个宽为3米的城门,他先横拿着进不去,又竖起来拿,结果竹竿比城门高1米,当他把竹竿斜着时,两端刚好顶着城门的对角,问竹竿长多少?
(2)在一棵树的10米高处B有两只猴子,其中一只猴子爬下树走到离树20米的池塘A,另一只猴子爬到树顶D后直接跃向池塘的A处,如果两只猴子所经过距离相等,试问这棵树有多高?
三.【变式拓展】
问题4.展开思想
1.如图为一棱长为3cm的正方体,把所有面都分为9个小正方形,其边长都是1cm,假设一只蚂蚁每秒爬行2cm,则它从下地面A点沿表面爬行至右侧面的B点,最少要花几秒钟?
2.如图是一个三级台阶,它的每一级长、宽、高分别是100cm,15cm和10cm,A,B是这个台阶上两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿台阶爬行到B点的最短路程是________.
【检学综练展成效】
1.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是_________.
(
第
4
题
)
三角形的三边长分别为 a2+b2、2ab、a2-b2(a、b都是正整数),则这个三角形是( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
如果把直角三角形的两条直角边同时扩大到原来的2倍,那么斜边扩大到原来的( )
A.1倍 B. 2倍 C. 3倍 D. 4倍
4.如图,直线上有三个正方形,若的面积分别为5和11,则的面积
= .
(
A
B
C
D
E
C
'
)5.将长方形ABCD沿直线BD折叠,使点C落在C'处,BC'交AD于E,AD=8,AB=4,
(1)△BED是 三角形,并说明理由.
(2)求△BED的面积.
6、如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
(1)判断∠D是否是直角,并说明理由.
(2)求四边形ABCD的面积.
7.如图,铁路A、B两站相距25km,C、D是两个工厂,位于铁路的同侧,其中,,且AC=15km,BD=10km
(1)尺规作图,在铁路AB上找一个点E建中转站,使得CE=DE,请作出这个点.
(
A
C
B
D
)(2)此时中转站E距A站多远
【校本作业】
一、必做题
1.在RtΔABC中,∠C=900(1)a=40,c=41,则b=______. (2)若a:c=6:10,c=20,则a=____,b=____ 2.若等腰三角形腰长为10cm,底边长为16 cm, 那么它的面积为 cm2.
3.若三角形的三边长a、b、c满足(a+b)2=c2+2ab,则这个三角形是( ).
(A)锐角三角形 (B)钝角三角形
(C)直角三角形 (D)何类三角形不能确定
4.“交通管理条例第三十五条”规定:小汽车在城街路上行驶速度不得超过千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方50米处,过了4秒后,测得小汽车与车速检测仪间距离为130米,这辆小汽车超速了吗?(提示:1米/秒=3.6千米/小时)
我国古代数学家赵爽用来证明勾股定理的弦图,可以说是充分肯定了我国数学的成就,也弘扬了我国古代的数学文化.弦图是由四个全等的直角三角形和中间的 小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么你能求出(a+b)2 的值吗?
二、选做题
6、如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.(1)求证:△ACE≌△BCD;(2)若AD=5,BD=12,求DE的长
三、拓展题
如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1) 观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2) 若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
