第12章 全等三角形 专题训练(无答案) 2023—2024学年人教版八年级数学上册
文档属性
| 名称 | 第12章 全等三角形 专题训练(无答案) 2023—2024学年人教版八年级数学上册 | 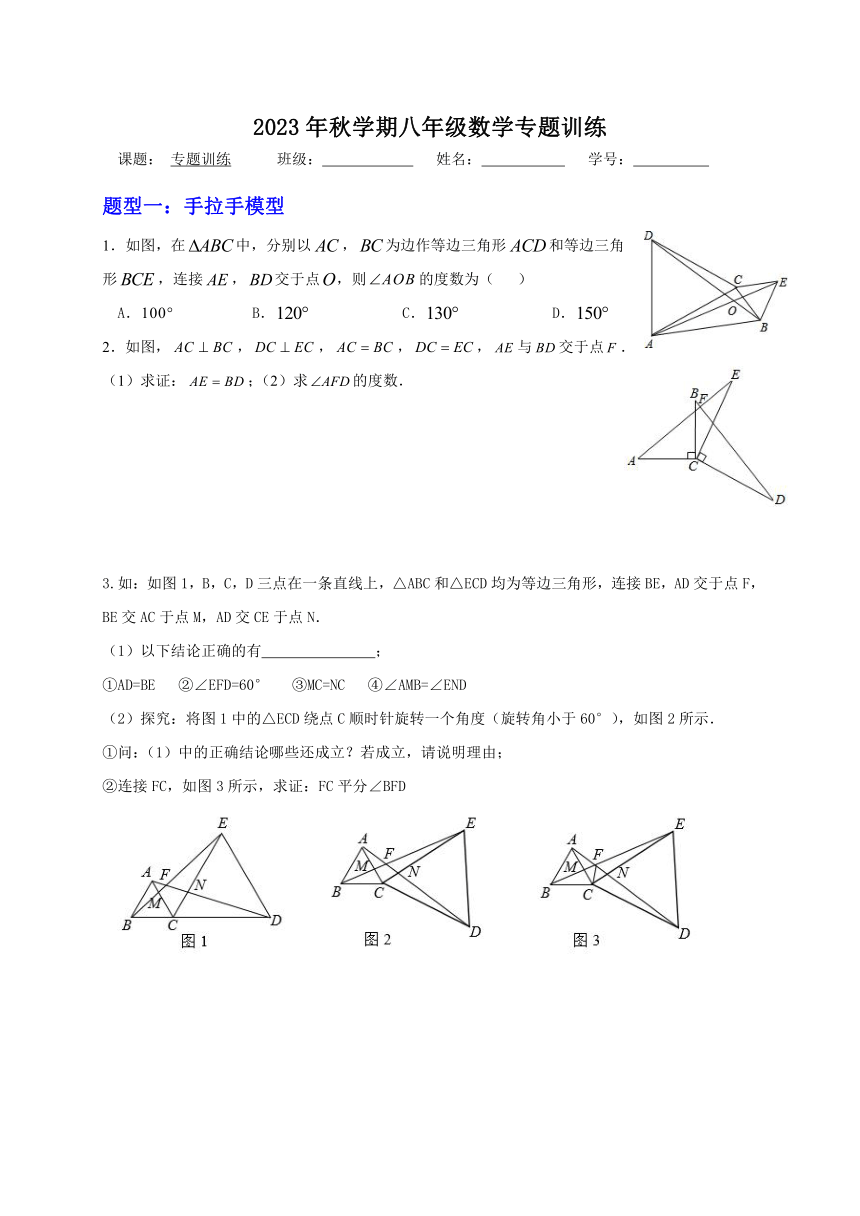 | |
| 格式 | docx | ||
| 文件大小 | 230.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-23 15:13:01 | ||
图片预览

文档简介
2023年秋学期八年级数学专题训练
课题: 专题训练 班级: 姓名: 学号:
题型一:手拉手模型
1.如图,在中,分别以,为边作等边三角形和等边三角形,连接,交于点,则的度数为( )
A. B. C. D.
2.如图,,,,,与交于点.
(1)求证:;(2)求的度数.
3.如:如图1,B,C,D三点在一条直线上,△ABC和△ECD均为等边三角形,连接BE,AD交于点F,BE交AC于点M,AD交CE于点N.
(1)以下结论正确的有 ;
①AD=BE ②∠EFD=60° ③MC=NC ④∠AMB=∠END
(2)探究:将图1中的△ECD绕点C顺时针旋转一个角度(旋转角小于60°),如图2所示.
①问:(1)中的正确结论哪些还成立?若成立,请说明理由;
②连接FC,如图3所示,求证:FC平分∠BFD
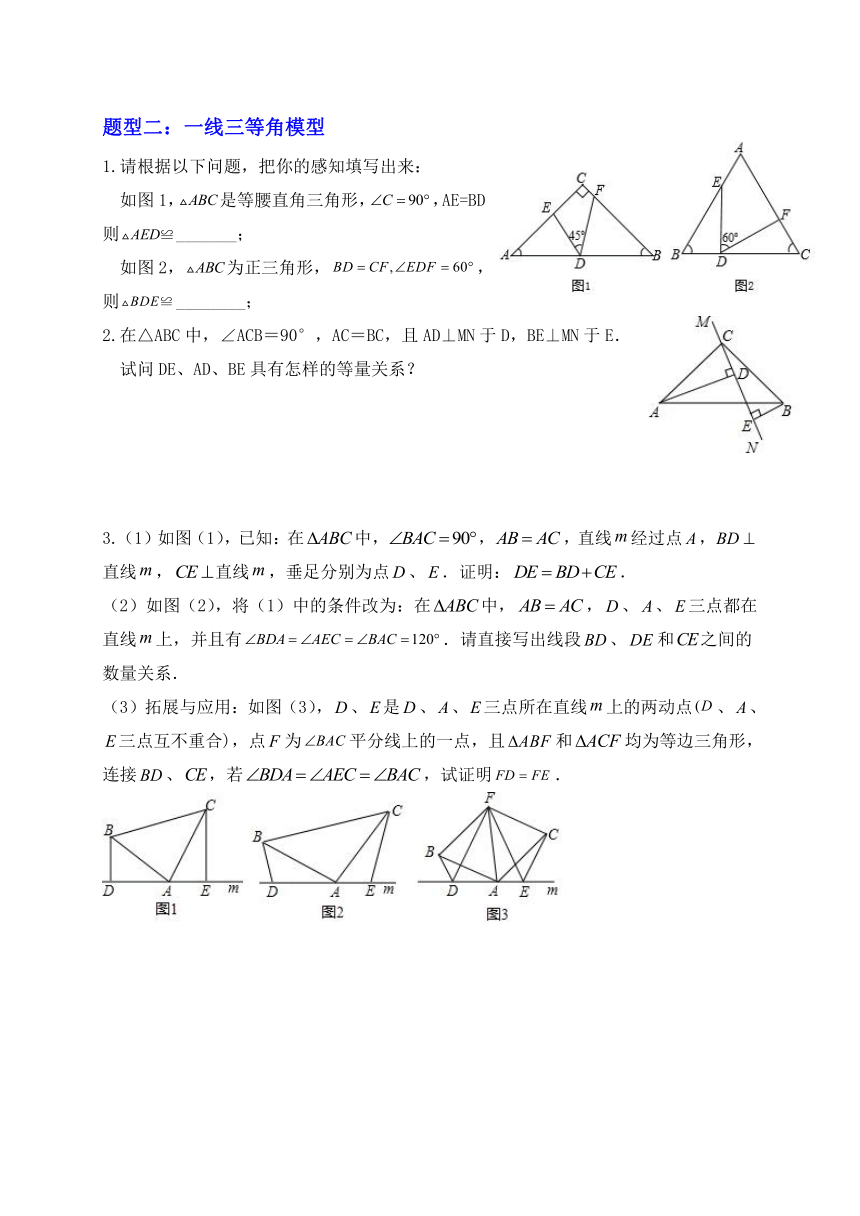
题型二:一线三等角模型
1.请根据以下问题,把你的感知填写出来:
如图1,是等腰直角三角形,,AE=BD,则_______;
如图2,为正三角形,,则________;
2.在△ABC中,∠ACB=90°,AC=BC,且AD⊥MN于D,BE⊥MN于E.
试问DE、AD、BE具有怎样的等量关系?
3.(1)如图(1),已知:在中,,,直线经过点,直线,直线,垂足分别为点、.证明:.
(2)如图(2),将(1)中的条件改为:在中,,、、三点都在直线上,并且有.请直接写出线段、和之间的数量关系.
(3)拓展与应用:如图(3),、是、、三点所在直线上的两动点、、三点互不重合),点为平分线上的一点,且和均为等边三角形,连接、,若,试证明.
题型三:倍长中线模型
1.如图,在△ABC中,AD交BC于点D,点E是BC的中点,EF∥AD交CA的延长线于点F,交AB于点G,BG=CF,求证:AD为∠BAC的平分线.
2.已知△ABC和△FDE均为含45°角的直角三角板。
(1)如图①所示摆放这两个三角板,点A与点F重合,连接BD、CE,取BD的中点G,连接AG,求证:CE=2AG;
(2)如图②所示摆放这两个三角板,点B与点D重合,连接CE,取CE的中点G,连接AG、GF,求证:AG=GF,AG⊥GF.
3.(1)如图①,若△ABC是直角三角形,∠BAC=90°,点D是BC的中点,延长AD到点E,使DE=AD,连接CE,可以得到△ABD≌△ECD,求证:△ACE是直角三角形;
(2)如图②,△ABC是直角三角形,∠BAC=90°,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF.试说明;
(3)如图③,在正方形ABCD中,E为AB边的中点,G、F分别为AD,BC边上的点,若AG=3,BF=4,∠GEF=90°,求GF的长.
题型四:半角模型
1.如图,为边长是1的等边三角形,为顶角是的等腰三角形,以为顶点作一个角,角的两边分别交、于、,连结,形成一个.求的周长.
2.如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是BC,CD上的点,且∠EAF是∠BAD的一半,那么结论EF=BE+FD是否成立?若成立,请证明;不成立,请说明理由.
3.问题背景:
如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;
课题: 专题训练 班级: 姓名: 学号:
题型一:手拉手模型
1.如图,在中,分别以,为边作等边三角形和等边三角形,连接,交于点,则的度数为( )
A. B. C. D.
2.如图,,,,,与交于点.
(1)求证:;(2)求的度数.
3.如:如图1,B,C,D三点在一条直线上,△ABC和△ECD均为等边三角形,连接BE,AD交于点F,BE交AC于点M,AD交CE于点N.
(1)以下结论正确的有 ;
①AD=BE ②∠EFD=60° ③MC=NC ④∠AMB=∠END
(2)探究:将图1中的△ECD绕点C顺时针旋转一个角度(旋转角小于60°),如图2所示.
①问:(1)中的正确结论哪些还成立?若成立,请说明理由;
②连接FC,如图3所示,求证:FC平分∠BFD
题型二:一线三等角模型
1.请根据以下问题,把你的感知填写出来:
如图1,是等腰直角三角形,,AE=BD,则_______;
如图2,为正三角形,,则________;
2.在△ABC中,∠ACB=90°,AC=BC,且AD⊥MN于D,BE⊥MN于E.
试问DE、AD、BE具有怎样的等量关系?
3.(1)如图(1),已知:在中,,,直线经过点,直线,直线,垂足分别为点、.证明:.
(2)如图(2),将(1)中的条件改为:在中,,、、三点都在直线上,并且有.请直接写出线段、和之间的数量关系.
(3)拓展与应用:如图(3),、是、、三点所在直线上的两动点、、三点互不重合),点为平分线上的一点,且和均为等边三角形,连接、,若,试证明.
题型三:倍长中线模型
1.如图,在△ABC中,AD交BC于点D,点E是BC的中点,EF∥AD交CA的延长线于点F,交AB于点G,BG=CF,求证:AD为∠BAC的平分线.
2.已知△ABC和△FDE均为含45°角的直角三角板。
(1)如图①所示摆放这两个三角板,点A与点F重合,连接BD、CE,取BD的中点G,连接AG,求证:CE=2AG;
(2)如图②所示摆放这两个三角板,点B与点D重合,连接CE,取CE的中点G,连接AG、GF,求证:AG=GF,AG⊥GF.
3.(1)如图①,若△ABC是直角三角形,∠BAC=90°,点D是BC的中点,延长AD到点E,使DE=AD,连接CE,可以得到△ABD≌△ECD,求证:△ACE是直角三角形;
(2)如图②,△ABC是直角三角形,∠BAC=90°,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF.试说明;
(3)如图③,在正方形ABCD中,E为AB边的中点,G、F分别为AD,BC边上的点,若AG=3,BF=4,∠GEF=90°,求GF的长.
题型四:半角模型
1.如图,为边长是1的等边三角形,为顶角是的等腰三角形,以为顶点作一个角,角的两边分别交、于、,连结,形成一个.求的周长.
2.如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是BC,CD上的点,且∠EAF是∠BAD的一半,那么结论EF=BE+FD是否成立?若成立,请证明;不成立,请说明理由.
3.问题背景:
如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;
