第1章勾股定理 综合训练题(含解析) 2023-20204学年北师大版八年级数学上册
文档属性
| 名称 | 第1章勾股定理 综合训练题(含解析) 2023-20204学年北师大版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 248.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-23 15:15:12 | ||
图片预览



文档简介
2023-20204学年北师大版八年级数学上册《第1章勾股定理》
综合训练题(附答案)
一、选择题
1.由线段a,b,c组成的三角形是直角三角形的是( )
A.a=1,b=2,c=3 B.a=2,b=3,c=4
C.a=3,b=4,c=5 D.a=4,b=5,c=6
2.现有一底面直径为5cm、高为12cm的圆柱形笔筒,小鹿将一根长度为14cm的铅笔放置其中,则铅笔上端露出笔筒的最短长度为( )
A.0cm B.1cm C.2cm D.3cm
3.将一个直角三角形的各边都扩大或缩小相同的倍数后,得到的三角形( )
A.可能是锐角三角形 B.不可能是直角三角形
C.仍然是直角三角形 D.可能是钝角三角形
4.如图,在四边形ABCD中,AC,BD相交于点O,且AC⊥BD,若AD=2,BC=4,则AB2+CD2的值为( )
A.8 B.14 C.20 D.26
5.如图,在△ABC中,过点A作BC的垂线交BC的延长线于点D,已知AC=13,BC=11,AD=12,则AB的长度为( )
A.15 B.16 C.18 D.20
6.如图,在等腰直角△ABC中,∠B=90°,AB=1,过点C作DC⊥AC且DC=1,再过点D作ED⊥AD且ED=1,则AE的长为( )
A. B.2 C. D.3
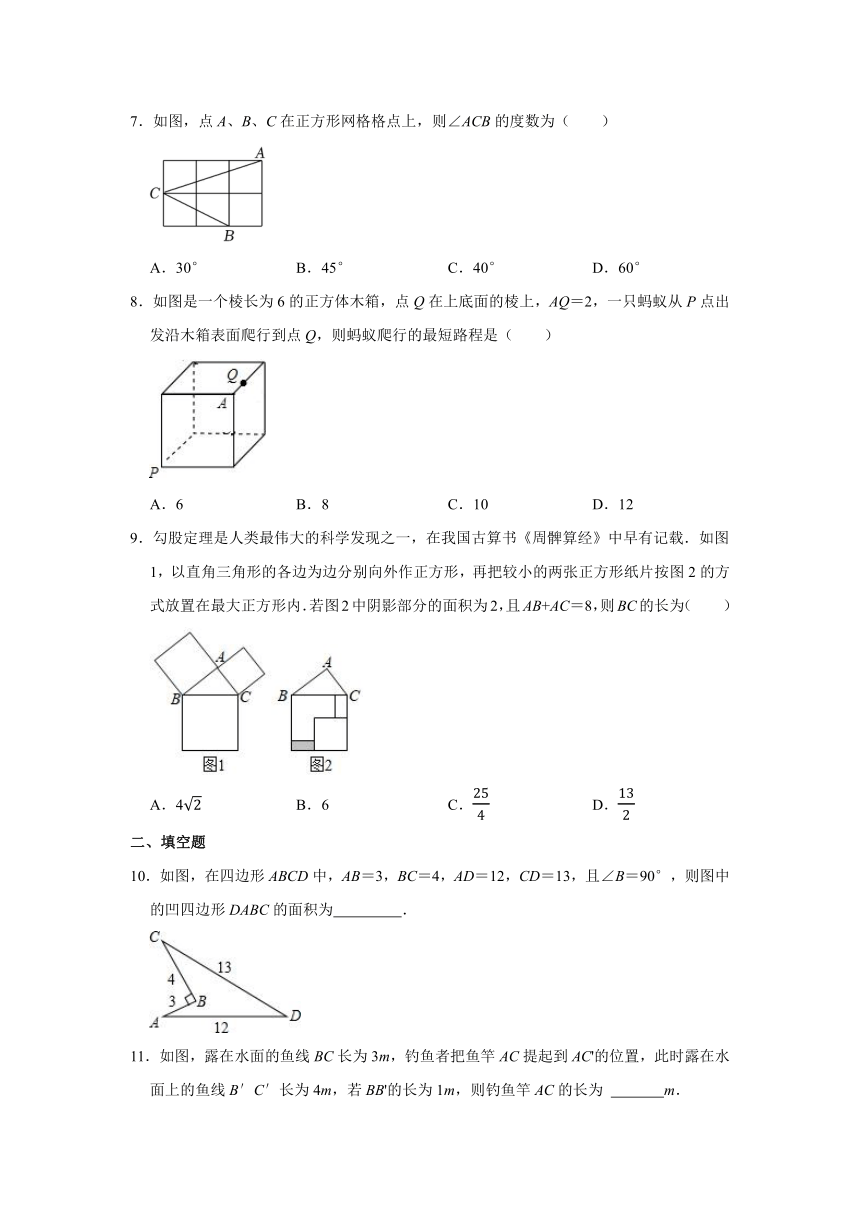
7.如图,点A、B、C在正方形网格格点上,则∠ACB的度数为( )
A.30° B.45° C.40° D.60°
8.如图是一个棱长为6的正方体木箱,点Q在上底面的棱上,AQ=2,一只蚂蚁从P点出发沿木箱表面爬行到点Q,则蚂蚁爬行的最短路程是( )
A.6 B.8 C.10 D.12
9.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若图2中阴影部分的面积为2,且AB+AC=8,则BC的长为( )
A.4 B.6 C. D.
二、填空题
10.如图,在四边形ABCD中,AB=3,BC=4,AD=12,CD=13,且∠B=90°,则图中的凹四边形DABC的面积为 .
11.如图,露在水面的鱼线BC长为3m,钓鱼者把鱼竿AC提起到AC'的位置,此时露在水面上的鱼线B′C′长为4m,若BB'的长为1m,则钓鱼竿AC的长为 m.
12.请写出一组勾股数 (三个数都要大于10).
13.如图,长方形ABCD中,AB在数轴上,AB=3,BC=1,若以点A为圆心,以AC长为半径画弧,交数轴于点M,则点M的表示的数为 .
14.如图,在水平桌面上依次摆着三个正方形,已知位于中间的正方形的面积为1,两边的正方形面积分别是S1,S2,则:S1+S2= .
15.如图,圆柱形玻璃杯,高为11cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 cm.
三、解答题
16.如图①是边长分别为a,b的两个正方形,经如图②所示的割补可以得到边长为c的正方形,且面积等于割补前两正方形的面积之和.利用这个方法可以验证勾股定理.
请根据上述信息回答下列问题:
(1)图②所示的割补过程为:割①补 ;割 补⑥;割③补 ;
(2)将图②完成拼接后得到图③,已知小正方形边长为2,且大正方形的边长为10,试计算其中一个直角三角形的周长.
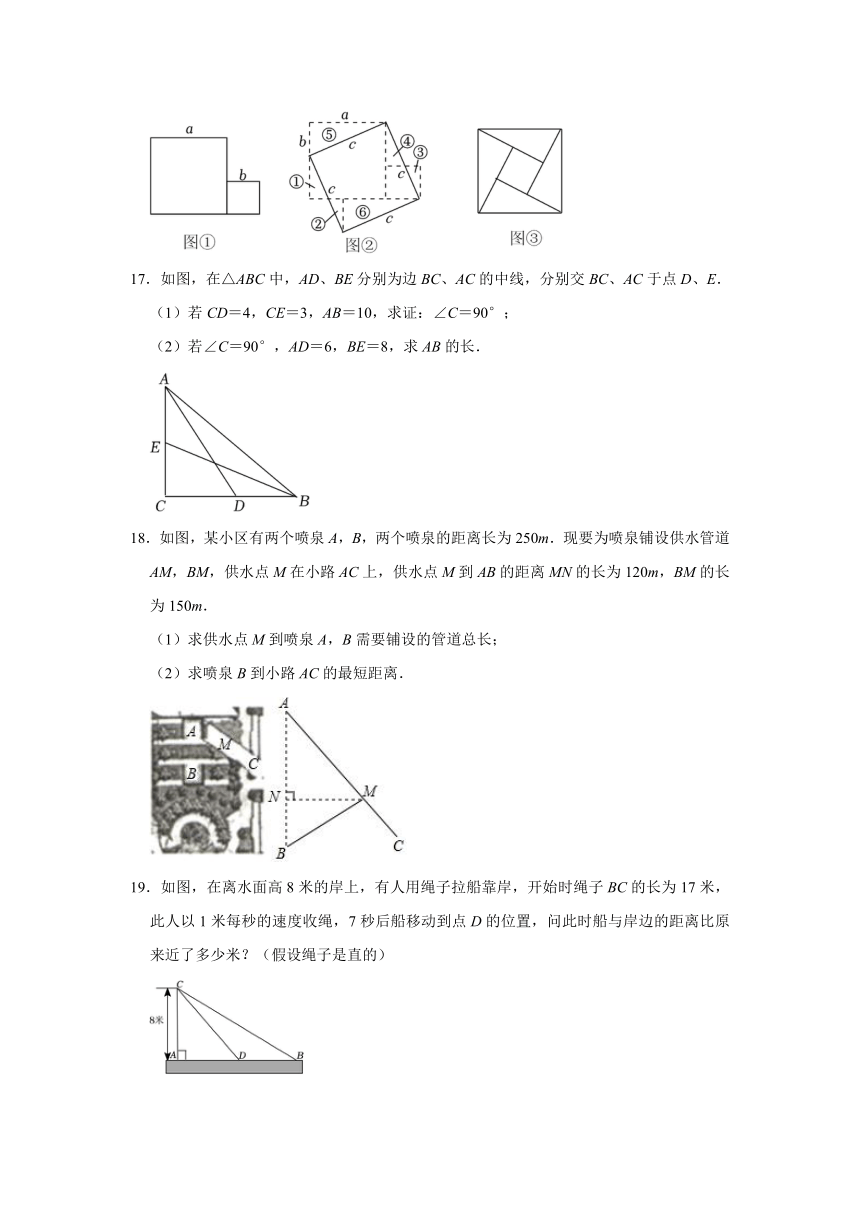
17.如图,在△ABC中,AD、BE分别为边BC、AC的中线,分别交BC、AC于点D、E.
(1)若CD=4,CE=3,AB=10,求证:∠C=90°;
(2)若∠C=90°,AD=6,BE=8,求AB的长.
18.如图,某小区有两个喷泉A,B,两个喷泉的距离长为250m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为120m,BM的长为150m.
(1)求供水点M到喷泉A,B需要铺设的管道总长;
(2)求喷泉B到小路AC的最短距离.
19.如图,在离水面高8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,此人以1米每秒的速度收绳,7秒后船移动到点D的位置,问此时船与岸边的距离比原来近了多少米?(假设绳子是直的)
20.如图,在长方形ABCD中,AB=4,BC=3,P为边BC上一点,将△CDP沿DP折叠,点C落在点E处,DE,PE分别交AB于点F,G,已知GE=GB.
(1)试说明:△GEF≌△GBP;
(2)求BF的长;
(3)求△EFG的面积.
参考答案
一、选择题
1.解:A、12+22≠32,不能构成直角三角形,故选项错误;
B、22+32≠42,不能构成直角三角形,故选项错误;
C、32+42=52,能构成直角三角形,故选项正确;
D、42+52≠62,不能构成直角三角形,故选项错误.
故选:C.
2.解:当铅笔与笔筒及笔筒的高构成直角三角形时h最小,
如图所示:AB13(cm),
故h=13﹣12=1(cm).
故选:B.
3.解:根据题意,新三角形与原三角形对应边成比例,
所以两个三角形相似,
所以得到的三角形仍然是直角三角形.
故选:C.
4.解:∵AC⊥BD,
∴AB2=AO2+BO2,CD2=OC2+OD2,BC2=BO2+CO2,AD2=OA2+OD2,
∴AB2+CD2=BC2+AD2,
∵AD=2,BC=4,
∴AB2+CD2=42+22=20,
故选:C.
5.解:∵AD⊥BC,
∴∠D=90°,
在Rt△ACD中,AC=13,AD=12,
∴CD,
∵BC=11,
∴BD=BC+CD=11+5=16,
在Rt△ABD中,AB,
故选:D.
6.解:在等腰直角△ABC中,∠B=90°,AB=1,
∴BC=AB=1,
∴AC,
∵DC⊥AC,DC=1,
∴AD,
∵ED⊥AD且ED=1,
∴AE,
故选:B.
7.解:连接AB,
设每个小正方形的边长为a,
ABa,BCa,ACa,
∴AB=BC,AB2+BC2=AC2,
∴△ABC是直角三角形,∠ACB=∠CAB,
∴∠ABC=90°,∠ACB=∠CAB=45°,
故选:B.
8.解:如图所示,
∵PB=AB=6,AQ=2,
∴BQ=6+2=8,
∴PQ10.
答:蚂蚁爬行的最短路程是10.
故选:C.
9.解:设AC=a,AB=b,BC=c,则a+b=8,c2=a2+b2,HG=c﹣b,DG=c﹣a,
则阴影部分的面积S=HG DG=(c﹣b)(c﹣a)=2,
∵(a+b)2=a2+b2+2ab=64,
∴ab=32,
∴S=c2﹣c(a+b)+ab=c2﹣8c+322,
解得c1=6,c2=10(舍去).
故选:B.
二、填空题
10.解:连接AC,如图所示:
∵∠B=90°,即△ABC为直角三角形,且AB=3,BC=4,
∴根据勾股定理得:AC5,
又∵AC2+AD2=52+122=25+144=169,CD2=132=169,
∴AC2+AD2=CD2,
∴∠CAD=90°,即△ACD为直角三角形,
则图中的凹四边形DABC的面积S=S△ACD﹣S△ABCAC ADAB BC=30﹣6=24.
故答案为:24.
11.解:设AB'=x,
∵AC'=AC,
∴AB'2+B'C'2=AB2+BC2,
即x2+42=(x+1)2+32,
解得:x=3,
∴AB=3+1=4,
∴,
故答案为:5.
12.解:∵162+122=202,
∴16,12,20是一组勾股数.
故答案为:16,12,20(答案不唯一).
13.解:∵AB=3,BC=1,
∴AC,
∵点A为圆心,AC的长为半径作弧交数轴于点M,
AM=AC,
∵A点表示﹣1,
∴M点表示的数为:1,
故答案为:1.
14.解:如图,
∵a、b、c都是正方形,
∴AC=CD,∠ACD=90°,
∴∠ACB+∠DCE=90°,
∵∠ACB+∠BAC=90°,
∴∠BAC=∠DCE,
在△ACB和△DCE中,
,
∴△ACB≌△CDE(AAS),
∴AB=CE,BC=DE;
在Rt△ABC中,由勾股定理得:AC2=AB2+BC2=AB2+DE2,
即Sb=Sa+Sc=1,
∴S1+S2=1.
故答案为:1.
15.解:如图,将杯子侧面展开,作A关于EF的对称点A′,
连接A′C,则A′C即为最短距离,
∵底面周长为18cm,
∴A'D=9cm,
∴A′C2=A′D2+CD2,
=92+122,
=225,
∴CA′=15cm,
答:蚂蚁到达蜂蜜的最短距离的是15cm;
故答案为15.
三、解答题
16.解:(1)如图②,∵四边形ABDE、四边形BCHL、四边形ACFG都是正方形,
∴∠GAC=∠ABD=∠BCE=∠AED=90°,AC=AG=a,AB=AE=BD=DE=c,BC=CH=BL=b,
∴∠BAC=∠EAG=90°﹣∠CAE,
∴△ABC≌△AEG(SAS),
∴BC=EG=b,∠ABC=∠AEG,
∵AC∥FG,
∴∠CAE=∠AEG,
∵∠QAH+∠CAE=90°,∠PEF+∠AEG=90°,
∴∠QAH=∠PEF,
∵AH=EF=a﹣b,∠AHQ=∠F=90°,
∴△AHQ≌△EFP(ASA),
∴割①补④;
∵DK⊥BF,
∴∠BKD=∠G=90°,
∵∠KBD+∠ABC=90°,∠GAE+∠AEG=90°,
∴∠KBD=∠GAE,
∴△KBD≌△GAE(AAS),
∴割⑤补⑥;
∵DE∥AB,BC∥HL,
∴∠DPK=∠ABC=∠BQL,
∵∠DKP=∠L=90°,DK=EG=BL=b,
∴△DKP≌△BLQ(AAS),
∴割③补②,
∴故答案为:④,⑤,②.
(2)如图②,∵小正方形边长为2,且大正方形的边长为10,
∴a﹣b=2,c=10,
∴a2+b2=c2=100,
由a﹣b=2得a2+b2﹣2ab=4,
∴100﹣2ab=4,
∴2ab=96,
∴(a+b)2=a2+b2+2ab=100+96=196,
∵a+b>0,
∴a+b=14,
∴a+b+c=14+10=24,
∴其中一个直角三角形的周长是24.
17.(1)证明:∵AD、BE分别为边BC、AC的中线,CD=4,CE=3,
∴AC=6,BC=8,
∵AB=10,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,
∴∠C=90°;
(2)解:∵∠C=90°,AD=6,BE=8,
∴AC2+CD2=AD2,BC2+CE2=BE2,
∵AD、BE分别为边BC、AC的中线,
∴CDBC,CEAC,
∴AC2+(BC)2=36,BC2+(AC)2=64,
∴AC2BC2=100,
∴AC2+BC2=80,
∴AB4.
18.解:(1)在Rt△MNB中,BN90(m),
∴AN=AB﹣BN=250﹣90=160(m),
在Rt△AMN中,AM200(m),
∴供水点M到喷泉A,B需要铺设的管道总长=200+150=350(m);
(2)∵AB=250m,AM=200m,BM=150m,
∴AB2=BM2+AM2,
∴△ABM是直角三角形,
∴BM⊥AC,
∴喷泉B到小路AC的最短距离是BM=150m.
19.解:在 Rt△ABC中,
∵∠CAB=90°,BC=17m,AC=8m,
∴.
依题意得CD=17﹣1×7=10m.
在 Rt△CAD中,,
DB=15﹣6=9m.
答:船离岸边距离比原来近了9m.
20.(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=90°,
由翻折的性质可知,∠E=∠C=90°,
∴∠E=∠B,
在△GEF和△GBP中,
,
∴△GEF≌△GBP(ASA);
(2)解:∵△GEF≌△GBF,
∴BF=EF,FG=GF,
∵GE=GB,
∴BF=PE,
设BF=EF=x,则PC=PE=BF=3﹣x,
∵DE=DC=4,
∴DF=4﹣x,
∵AF=AB﹣BF=4﹣(3﹣x)=1+x,∠A=90°,
∴AD2=AF2+DF2,
∴32+(1+x)2=(4﹣x)2,
∴x,
∴BF=CP=3;
(3)解:∵∠A=∠E=90°,∠AFD=∠EFG,
∴AD=3,AF=1,EF,
∴,
∴EG,
∴S△EFG EF EG.
综合训练题(附答案)
一、选择题
1.由线段a,b,c组成的三角形是直角三角形的是( )
A.a=1,b=2,c=3 B.a=2,b=3,c=4
C.a=3,b=4,c=5 D.a=4,b=5,c=6
2.现有一底面直径为5cm、高为12cm的圆柱形笔筒,小鹿将一根长度为14cm的铅笔放置其中,则铅笔上端露出笔筒的最短长度为( )
A.0cm B.1cm C.2cm D.3cm
3.将一个直角三角形的各边都扩大或缩小相同的倍数后,得到的三角形( )
A.可能是锐角三角形 B.不可能是直角三角形
C.仍然是直角三角形 D.可能是钝角三角形
4.如图,在四边形ABCD中,AC,BD相交于点O,且AC⊥BD,若AD=2,BC=4,则AB2+CD2的值为( )
A.8 B.14 C.20 D.26
5.如图,在△ABC中,过点A作BC的垂线交BC的延长线于点D,已知AC=13,BC=11,AD=12,则AB的长度为( )
A.15 B.16 C.18 D.20
6.如图,在等腰直角△ABC中,∠B=90°,AB=1,过点C作DC⊥AC且DC=1,再过点D作ED⊥AD且ED=1,则AE的长为( )
A. B.2 C. D.3
7.如图,点A、B、C在正方形网格格点上,则∠ACB的度数为( )
A.30° B.45° C.40° D.60°
8.如图是一个棱长为6的正方体木箱,点Q在上底面的棱上,AQ=2,一只蚂蚁从P点出发沿木箱表面爬行到点Q,则蚂蚁爬行的最短路程是( )
A.6 B.8 C.10 D.12
9.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若图2中阴影部分的面积为2,且AB+AC=8,则BC的长为( )
A.4 B.6 C. D.
二、填空题
10.如图,在四边形ABCD中,AB=3,BC=4,AD=12,CD=13,且∠B=90°,则图中的凹四边形DABC的面积为 .
11.如图,露在水面的鱼线BC长为3m,钓鱼者把鱼竿AC提起到AC'的位置,此时露在水面上的鱼线B′C′长为4m,若BB'的长为1m,则钓鱼竿AC的长为 m.
12.请写出一组勾股数 (三个数都要大于10).
13.如图,长方形ABCD中,AB在数轴上,AB=3,BC=1,若以点A为圆心,以AC长为半径画弧,交数轴于点M,则点M的表示的数为 .
14.如图,在水平桌面上依次摆着三个正方形,已知位于中间的正方形的面积为1,两边的正方形面积分别是S1,S2,则:S1+S2= .
15.如图,圆柱形玻璃杯,高为11cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 cm.
三、解答题
16.如图①是边长分别为a,b的两个正方形,经如图②所示的割补可以得到边长为c的正方形,且面积等于割补前两正方形的面积之和.利用这个方法可以验证勾股定理.
请根据上述信息回答下列问题:
(1)图②所示的割补过程为:割①补 ;割 补⑥;割③补 ;
(2)将图②完成拼接后得到图③,已知小正方形边长为2,且大正方形的边长为10,试计算其中一个直角三角形的周长.
17.如图,在△ABC中,AD、BE分别为边BC、AC的中线,分别交BC、AC于点D、E.
(1)若CD=4,CE=3,AB=10,求证:∠C=90°;
(2)若∠C=90°,AD=6,BE=8,求AB的长.
18.如图,某小区有两个喷泉A,B,两个喷泉的距离长为250m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为120m,BM的长为150m.
(1)求供水点M到喷泉A,B需要铺设的管道总长;
(2)求喷泉B到小路AC的最短距离.
19.如图,在离水面高8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,此人以1米每秒的速度收绳,7秒后船移动到点D的位置,问此时船与岸边的距离比原来近了多少米?(假设绳子是直的)
20.如图,在长方形ABCD中,AB=4,BC=3,P为边BC上一点,将△CDP沿DP折叠,点C落在点E处,DE,PE分别交AB于点F,G,已知GE=GB.
(1)试说明:△GEF≌△GBP;
(2)求BF的长;
(3)求△EFG的面积.
参考答案
一、选择题
1.解:A、12+22≠32,不能构成直角三角形,故选项错误;
B、22+32≠42,不能构成直角三角形,故选项错误;
C、32+42=52,能构成直角三角形,故选项正确;
D、42+52≠62,不能构成直角三角形,故选项错误.
故选:C.
2.解:当铅笔与笔筒及笔筒的高构成直角三角形时h最小,
如图所示:AB13(cm),
故h=13﹣12=1(cm).
故选:B.
3.解:根据题意,新三角形与原三角形对应边成比例,
所以两个三角形相似,
所以得到的三角形仍然是直角三角形.
故选:C.
4.解:∵AC⊥BD,
∴AB2=AO2+BO2,CD2=OC2+OD2,BC2=BO2+CO2,AD2=OA2+OD2,
∴AB2+CD2=BC2+AD2,
∵AD=2,BC=4,
∴AB2+CD2=42+22=20,
故选:C.
5.解:∵AD⊥BC,
∴∠D=90°,
在Rt△ACD中,AC=13,AD=12,
∴CD,
∵BC=11,
∴BD=BC+CD=11+5=16,
在Rt△ABD中,AB,
故选:D.
6.解:在等腰直角△ABC中,∠B=90°,AB=1,
∴BC=AB=1,
∴AC,
∵DC⊥AC,DC=1,
∴AD,
∵ED⊥AD且ED=1,
∴AE,
故选:B.
7.解:连接AB,
设每个小正方形的边长为a,
ABa,BCa,ACa,
∴AB=BC,AB2+BC2=AC2,
∴△ABC是直角三角形,∠ACB=∠CAB,
∴∠ABC=90°,∠ACB=∠CAB=45°,
故选:B.
8.解:如图所示,
∵PB=AB=6,AQ=2,
∴BQ=6+2=8,
∴PQ10.
答:蚂蚁爬行的最短路程是10.
故选:C.
9.解:设AC=a,AB=b,BC=c,则a+b=8,c2=a2+b2,HG=c﹣b,DG=c﹣a,
则阴影部分的面积S=HG DG=(c﹣b)(c﹣a)=2,
∵(a+b)2=a2+b2+2ab=64,
∴ab=32,
∴S=c2﹣c(a+b)+ab=c2﹣8c+322,
解得c1=6,c2=10(舍去).
故选:B.
二、填空题
10.解:连接AC,如图所示:
∵∠B=90°,即△ABC为直角三角形,且AB=3,BC=4,
∴根据勾股定理得:AC5,
又∵AC2+AD2=52+122=25+144=169,CD2=132=169,
∴AC2+AD2=CD2,
∴∠CAD=90°,即△ACD为直角三角形,
则图中的凹四边形DABC的面积S=S△ACD﹣S△ABCAC ADAB BC=30﹣6=24.
故答案为:24.
11.解:设AB'=x,
∵AC'=AC,
∴AB'2+B'C'2=AB2+BC2,
即x2+42=(x+1)2+32,
解得:x=3,
∴AB=3+1=4,
∴,
故答案为:5.
12.解:∵162+122=202,
∴16,12,20是一组勾股数.
故答案为:16,12,20(答案不唯一).
13.解:∵AB=3,BC=1,
∴AC,
∵点A为圆心,AC的长为半径作弧交数轴于点M,
AM=AC,
∵A点表示﹣1,
∴M点表示的数为:1,
故答案为:1.
14.解:如图,
∵a、b、c都是正方形,
∴AC=CD,∠ACD=90°,
∴∠ACB+∠DCE=90°,
∵∠ACB+∠BAC=90°,
∴∠BAC=∠DCE,
在△ACB和△DCE中,
,
∴△ACB≌△CDE(AAS),
∴AB=CE,BC=DE;
在Rt△ABC中,由勾股定理得:AC2=AB2+BC2=AB2+DE2,
即Sb=Sa+Sc=1,
∴S1+S2=1.
故答案为:1.
15.解:如图,将杯子侧面展开,作A关于EF的对称点A′,
连接A′C,则A′C即为最短距离,
∵底面周长为18cm,
∴A'D=9cm,
∴A′C2=A′D2+CD2,
=92+122,
=225,
∴CA′=15cm,
答:蚂蚁到达蜂蜜的最短距离的是15cm;
故答案为15.
三、解答题
16.解:(1)如图②,∵四边形ABDE、四边形BCHL、四边形ACFG都是正方形,
∴∠GAC=∠ABD=∠BCE=∠AED=90°,AC=AG=a,AB=AE=BD=DE=c,BC=CH=BL=b,
∴∠BAC=∠EAG=90°﹣∠CAE,
∴△ABC≌△AEG(SAS),
∴BC=EG=b,∠ABC=∠AEG,
∵AC∥FG,
∴∠CAE=∠AEG,
∵∠QAH+∠CAE=90°,∠PEF+∠AEG=90°,
∴∠QAH=∠PEF,
∵AH=EF=a﹣b,∠AHQ=∠F=90°,
∴△AHQ≌△EFP(ASA),
∴割①补④;
∵DK⊥BF,
∴∠BKD=∠G=90°,
∵∠KBD+∠ABC=90°,∠GAE+∠AEG=90°,
∴∠KBD=∠GAE,
∴△KBD≌△GAE(AAS),
∴割⑤补⑥;
∵DE∥AB,BC∥HL,
∴∠DPK=∠ABC=∠BQL,
∵∠DKP=∠L=90°,DK=EG=BL=b,
∴△DKP≌△BLQ(AAS),
∴割③补②,
∴故答案为:④,⑤,②.
(2)如图②,∵小正方形边长为2,且大正方形的边长为10,
∴a﹣b=2,c=10,
∴a2+b2=c2=100,
由a﹣b=2得a2+b2﹣2ab=4,
∴100﹣2ab=4,
∴2ab=96,
∴(a+b)2=a2+b2+2ab=100+96=196,
∵a+b>0,
∴a+b=14,
∴a+b+c=14+10=24,
∴其中一个直角三角形的周长是24.
17.(1)证明:∵AD、BE分别为边BC、AC的中线,CD=4,CE=3,
∴AC=6,BC=8,
∵AB=10,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,
∴∠C=90°;
(2)解:∵∠C=90°,AD=6,BE=8,
∴AC2+CD2=AD2,BC2+CE2=BE2,
∵AD、BE分别为边BC、AC的中线,
∴CDBC,CEAC,
∴AC2+(BC)2=36,BC2+(AC)2=64,
∴AC2BC2=100,
∴AC2+BC2=80,
∴AB4.
18.解:(1)在Rt△MNB中,BN90(m),
∴AN=AB﹣BN=250﹣90=160(m),
在Rt△AMN中,AM200(m),
∴供水点M到喷泉A,B需要铺设的管道总长=200+150=350(m);
(2)∵AB=250m,AM=200m,BM=150m,
∴AB2=BM2+AM2,
∴△ABM是直角三角形,
∴BM⊥AC,
∴喷泉B到小路AC的最短距离是BM=150m.
19.解:在 Rt△ABC中,
∵∠CAB=90°,BC=17m,AC=8m,
∴.
依题意得CD=17﹣1×7=10m.
在 Rt△CAD中,,
DB=15﹣6=9m.
答:船离岸边距离比原来近了9m.
20.(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=90°,
由翻折的性质可知,∠E=∠C=90°,
∴∠E=∠B,
在△GEF和△GBP中,
,
∴△GEF≌△GBP(ASA);
(2)解:∵△GEF≌△GBF,
∴BF=EF,FG=GF,
∵GE=GB,
∴BF=PE,
设BF=EF=x,则PC=PE=BF=3﹣x,
∵DE=DC=4,
∴DF=4﹣x,
∵AF=AB﹣BF=4﹣(3﹣x)=1+x,∠A=90°,
∴AD2=AF2+DF2,
∴32+(1+x)2=(4﹣x)2,
∴x,
∴BF=CP=3;
(3)解:∵∠A=∠E=90°,∠AFD=∠EFG,
∴AD=3,AF=1,EF,
∴,
∴EG,
∴S△EFG EF EG.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
