多边形内角和
图片预览


文档简介
课件17张PPT。7.3.2多边形的内角和问题2:你知道长方形和正方形的内角和是多
少度吗?
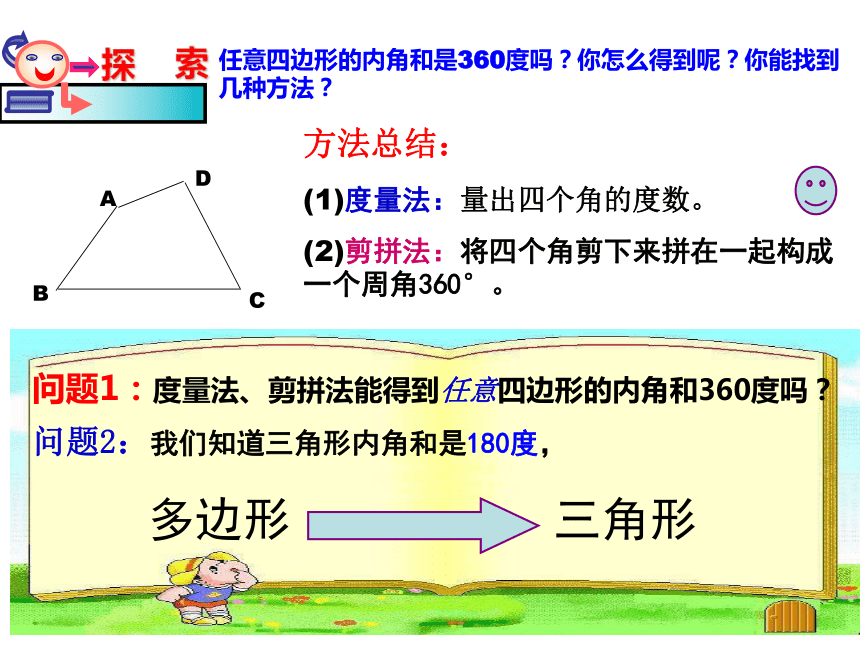
问题1:你还记得三角形内角和是多少度吗?(三角形内角和 180°)(都是360°)回顾: 那是不是任意四边形的内角和都是360°呢?猜测:任意四边形的内角和是360度吗?你怎么得到呢?你能找到几种方法?方法总结:
(1)度量法:量出四个角的度数。
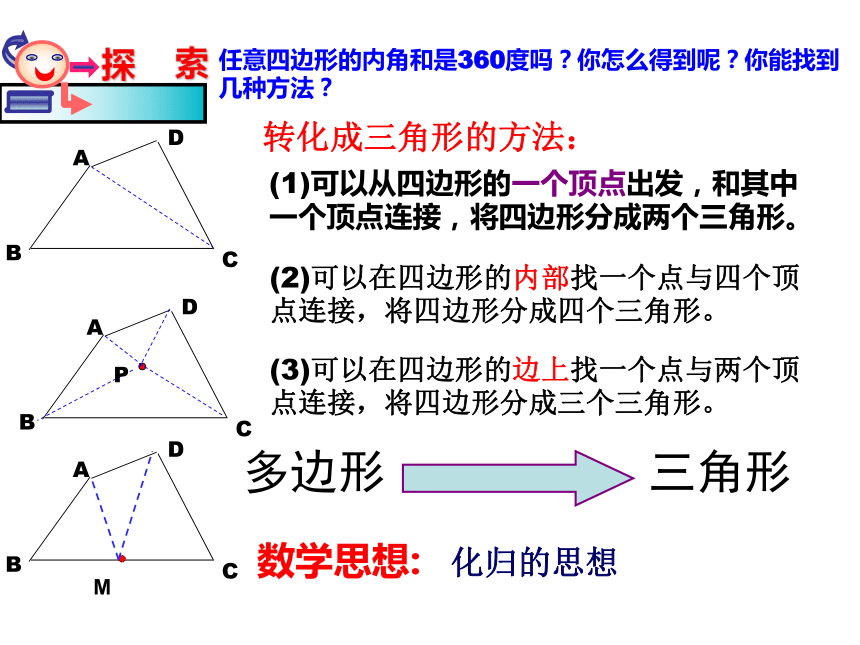
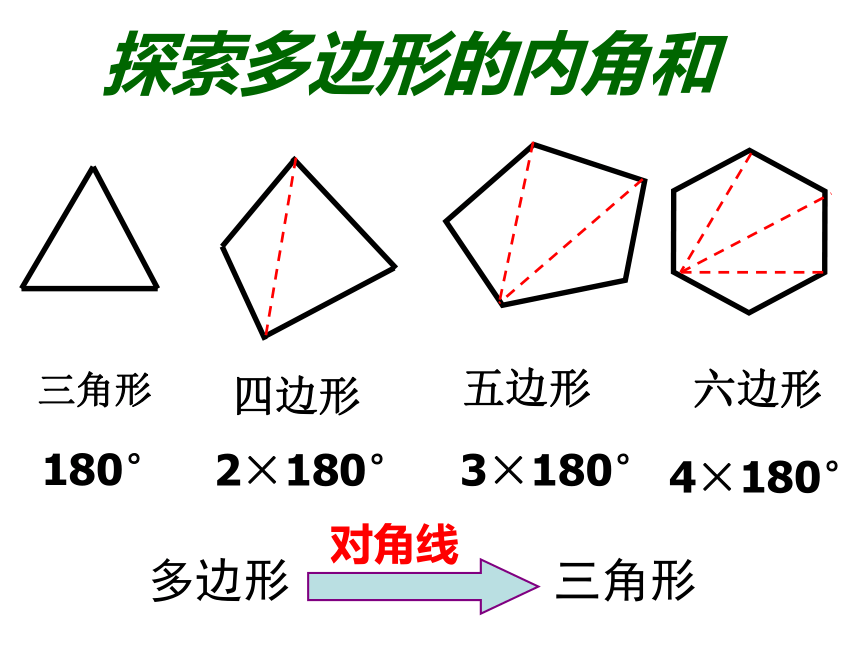
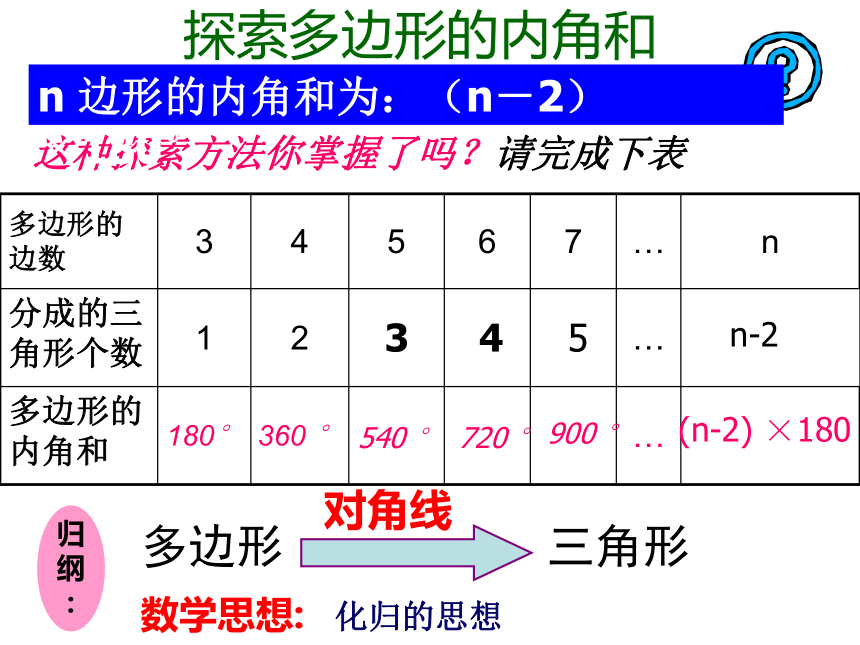
(2)剪拼法:将四个角剪下来拼在一起构成一个周角360°。问题1:度量法、剪拼法能得到任意四边形的内角和360度吗?问题2:我们知道三角形内角和是180度,多边形三角形任意四边形的内角和是360度吗?你怎么得到呢?你能找到几种方法?P转化成三角形的方法:M(2)可以在四边形的内部找一个点与四个顶点连接,将四边形分成四个三角形。(1)可以从四边形的一个顶点出发,和其中一个顶点连接,将四边形分成两个三角形。(3)可以在四边形的边上找一个点与两个顶点连接,将四边形分成三个三角形。数学思想: 化归的思想探索多边形的内角和180°2×180°3×180°4×180°对角线探索多边形的内角和这种探索方法你掌握了吗?请完成下表345n-2900 °(n-2) ×180720 °540 °n 边形的内角和为:(n-2)×180°数学思想: 化归的思想归
纲
:多边形的内角和1、快速抢答,熟悉公式(1)、8边形的内角和是 。
(2)、12边形的内角和是 。
(3)、一个多边形的内角和是1440°,它是 边形。
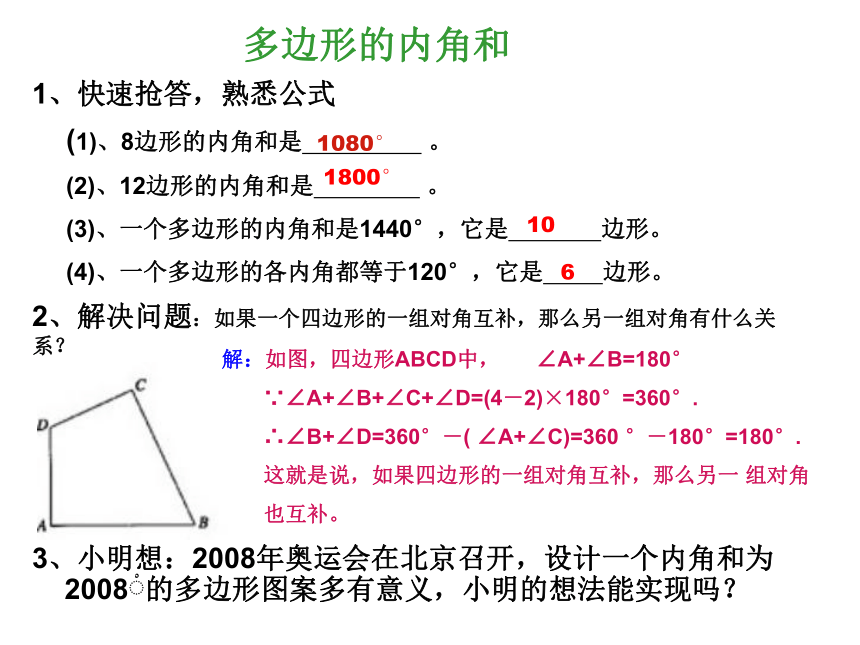
(4)、一个多边形的各内角都等于120°,它是 边形。2、解决问题:如果一个四边形的一组对角互补,那么另一组对角有什么关系?解:如图,四边形ABCD中, ∠A+∠B=180°
∵∠A+∠B+∠C+∠D=(4-2)×180°=360°.
∴∠B+∠D=360°-( ∠A+∠C)=360 °-180°=180°.
这就是说,如果四边形的一组对角互补,那么另一 组对角
也互补。1080°1800° 1063、小明想:2008年奥运会在北京召开,设计一个内角和为2008?的多边形图案多有意义,小明的想法能实现吗?4、在四边形ABCD中,∠A=120度,∠B:∠C:∠D = 3:4:5,求∠B,∠C,∠D的度数。解:设∠B,∠C,∠D的度数分别是3x , 4x , 5x 度,由四边形的内角和等于360度可得: 120 + 3x + 4x + 5x = 360 12x = 240 x = 20∴ 3x = 60
4x = 80
5x = 100答:∠B,∠C,∠D的度数分别为60,80, 100度。5、 一个多边形当边数增加1时,它的内角和增加 多少度?当边数增加1时,
解: 设多边形的边数为n,
因为它的内角和等于 (n-2)?180°,? (n+1-2)?180°- (n-2)?180°
=n?180°-180°- n?180°+360°
= 180°
?内角和增加180° 内角和为(n+1-2)?180°,多边形的外角和清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步。(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?
(2)他每跑完一圈,身体转过的角度之和是多少?(3)在上图中,?1+ ? 2+ ? 3+ ? 4+ ? 5=?你是怎样得到的? 演示实验的方法360°方法总结:
(1)度量法:量出五个外角的度数。
(2)剪拼法:将五个外角剪下来拼在一起。?1+ ? 2+ ? 3+ ? 4+ ? 5=你能对这个结论进行推理证明吗?解:∵∠1+∠6=180°,
∠2+∠7=180°,
∠3+∠8=180°,
∠4+∠9=180°,
∠5+∠10=180° ∴∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8+∠9+∠10
=180×5=900°∴ ∠1+∠2+∠3+∠4+∠5 =360° ∵∠6+∠7+∠8+∠9+∠10 =(5-2)×180°=540° 推理证明法:回顾:360°360°360°360°360°猜测:难道n边形的外角和也是360°?n边形的外角和=n个平角-内角和
结论:多边形的外角和等于360°=n×180°-(n-2) × 180°
= 360°3×180o-180o=360o4×180o-360o=360o5×180o-540o=360on×180o-(n-2)×180o=360o(探索任意多边形的外角和)合作学习:[例]一个多边形的内角和等于它的外角和的3倍,它是几边形? 解:设这个多边形是n边形,则它的内角和是
(n-2)·180°,外角和等于360°,
∴ (n-2)·180=3×360
解得:n=8
答:这个多边形是八边形. 例题赏析1、正五边形的每一个外角等于___.每一个内角等于_____,72°144°3、如果一个正多边形的一个内角等于150°,则这个多边形的边数是_____A.12 B.9 C. 8 D.7A4、如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____12练习:2、正n边形的每一个外角等于___.每一个内角等于 ,这节课你学到了什么?感悟与反思n 边形的内角和为:(n-2)×180°n 边形的内角和为:(n-2)×180°1.多边形的内角和: (n-2)×180°
2.多边形的外角和是 360°
3.数学思想方法: 化归
多边形 三角形对角线
少度吗?
问题1:你还记得三角形内角和是多少度吗?(三角形内角和 180°)(都是360°)回顾: 那是不是任意四边形的内角和都是360°呢?猜测:任意四边形的内角和是360度吗?你怎么得到呢?你能找到几种方法?方法总结:
(1)度量法:量出四个角的度数。
(2)剪拼法:将四个角剪下来拼在一起构成一个周角360°。问题1:度量法、剪拼法能得到任意四边形的内角和360度吗?问题2:我们知道三角形内角和是180度,多边形三角形任意四边形的内角和是360度吗?你怎么得到呢?你能找到几种方法?P转化成三角形的方法:M(2)可以在四边形的内部找一个点与四个顶点连接,将四边形分成四个三角形。(1)可以从四边形的一个顶点出发,和其中一个顶点连接,将四边形分成两个三角形。(3)可以在四边形的边上找一个点与两个顶点连接,将四边形分成三个三角形。数学思想: 化归的思想探索多边形的内角和180°2×180°3×180°4×180°对角线探索多边形的内角和这种探索方法你掌握了吗?请完成下表345n-2900 °(n-2) ×180720 °540 °n 边形的内角和为:(n-2)×180°数学思想: 化归的思想归
纲
:多边形的内角和1、快速抢答,熟悉公式(1)、8边形的内角和是 。
(2)、12边形的内角和是 。
(3)、一个多边形的内角和是1440°,它是 边形。
(4)、一个多边形的各内角都等于120°,它是 边形。2、解决问题:如果一个四边形的一组对角互补,那么另一组对角有什么关系?解:如图,四边形ABCD中, ∠A+∠B=180°
∵∠A+∠B+∠C+∠D=(4-2)×180°=360°.
∴∠B+∠D=360°-( ∠A+∠C)=360 °-180°=180°.
这就是说,如果四边形的一组对角互补,那么另一 组对角
也互补。1080°1800° 1063、小明想:2008年奥运会在北京召开,设计一个内角和为2008?的多边形图案多有意义,小明的想法能实现吗?4、在四边形ABCD中,∠A=120度,∠B:∠C:∠D = 3:4:5,求∠B,∠C,∠D的度数。解:设∠B,∠C,∠D的度数分别是3x , 4x , 5x 度,由四边形的内角和等于360度可得: 120 + 3x + 4x + 5x = 360 12x = 240 x = 20∴ 3x = 60
4x = 80
5x = 100答:∠B,∠C,∠D的度数分别为60,80, 100度。5、 一个多边形当边数增加1时,它的内角和增加 多少度?当边数增加1时,
解: 设多边形的边数为n,
因为它的内角和等于 (n-2)?180°,? (n+1-2)?180°- (n-2)?180°
=n?180°-180°- n?180°+360°
= 180°
?内角和增加180° 内角和为(n+1-2)?180°,多边形的外角和清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步。(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?
(2)他每跑完一圈,身体转过的角度之和是多少?(3)在上图中,?1+ ? 2+ ? 3+ ? 4+ ? 5=?你是怎样得到的? 演示实验的方法360°方法总结:
(1)度量法:量出五个外角的度数。
(2)剪拼法:将五个外角剪下来拼在一起。?1+ ? 2+ ? 3+ ? 4+ ? 5=你能对这个结论进行推理证明吗?解:∵∠1+∠6=180°,
∠2+∠7=180°,
∠3+∠8=180°,
∠4+∠9=180°,
∠5+∠10=180° ∴∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8+∠9+∠10
=180×5=900°∴ ∠1+∠2+∠3+∠4+∠5 =360° ∵∠6+∠7+∠8+∠9+∠10 =(5-2)×180°=540° 推理证明法:回顾:360°360°360°360°360°猜测:难道n边形的外角和也是360°?n边形的外角和=n个平角-内角和
结论:多边形的外角和等于360°=n×180°-(n-2) × 180°
= 360°3×180o-180o=360o4×180o-360o=360o5×180o-540o=360on×180o-(n-2)×180o=360o(探索任意多边形的外角和)合作学习:[例]一个多边形的内角和等于它的外角和的3倍,它是几边形? 解:设这个多边形是n边形,则它的内角和是
(n-2)·180°,外角和等于360°,
∴ (n-2)·180=3×360
解得:n=8
答:这个多边形是八边形. 例题赏析1、正五边形的每一个外角等于___.每一个内角等于_____,72°144°3、如果一个正多边形的一个内角等于150°,则这个多边形的边数是_____A.12 B.9 C. 8 D.7A4、如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____12练习:2、正n边形的每一个外角等于___.每一个内角等于 ,这节课你学到了什么?感悟与反思n 边形的内角和为:(n-2)×180°n 边形的内角和为:(n-2)×180°1.多边形的内角和: (n-2)×180°
2.多边形的外角和是 360°
3.数学思想方法: 化归
多边形 三角形对角线
