第三章 勾股定理 单元提高试卷(无答案) 苏科版数学八年级上册
文档属性
| 名称 | 第三章 勾股定理 单元提高试卷(无答案) 苏科版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 292.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-23 00:00:00 | ||
图片预览


文档简介
第三章 勾股定理
一、选择题
在 中,,, 的对边分别是 ,,,下列命题中的假命题是
A.若 ,则
B.若 ,则 不是直角三角形
C.若 ,则
D.若 ,则
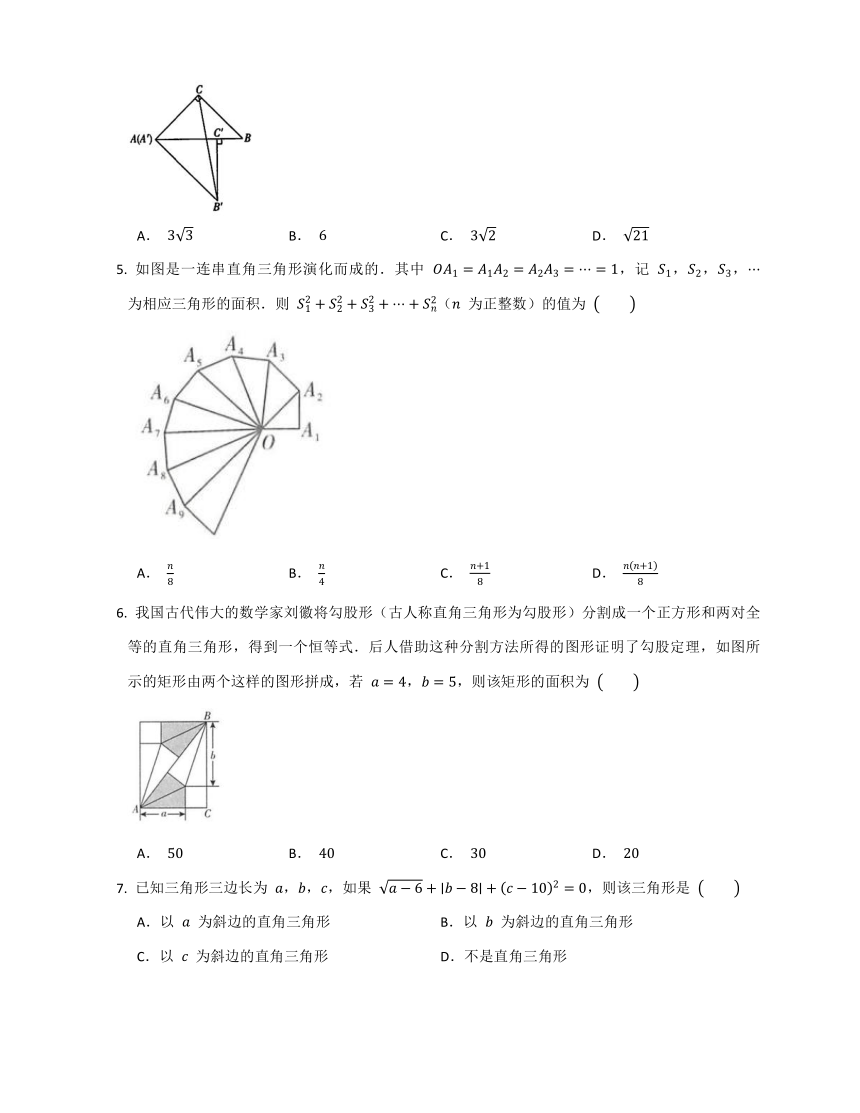
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形 ,,, 的面积分别是 ,,,,则最大正方形 的边长是
A. B. C. D.无法确定
五根小木棒,其长度分别为 ,,,,,现将它们摆成各选项所示的两个直角三角形,其中正确的是
A. B.
C. D.
如图,将两个大小、形状完全相同的 和 拼在一起,其中点 与点 重合,点 落在边 上,连接 .若 ,,则 的长为
A. B. C. D.
如图是一连串直角三角形演化而成的.其中 ,记 ,,, 为相应三角形的面积.则 ( 为正整数)的值为
A. B. C. D.
我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若 ,,则该矩形的面积为
A. B. C. D.
已知三角形三边长为 ,,,如果 ,则该三角形是
A.以 为斜边的直角三角形 B.以 为斜边的直角三角形
C.以 为斜边的直角三角形 D.不是直角三角形
如图,在四边形 中,,,,.分别以点 , 为圆心,大于 的长为半径作弧,两弧交于点 ,作射线 交 于点 ,交 于点 .若 是 的中点,则 的长为
A. B. C. D.
二、填空题
把两个同样大小的含 角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点 ,且另三个锐角顶点 ,, 在同一直线上.若 ,则 .
如图,有一块田地的形状和尺寸如图所示,则它的面积为 .
如图,有一棱长为 的正方体盒子,现要按图中箭头所指方向从点 到点 拉一条捆绑线绳,使线绳经过 ,,, 四个面,则所需捆绑线绳的长至少为 .
如图,在 中,,,过点 作 ,连接 ,,过点 作 于点 ,若 , 的面积为 ,则 的长为 .
如图,已知直角三角形 中, 为直角,,,三角形 为等腰三角形,其中 ,且 , 为 中点,连接 ,,,则三角形 的面积为 .
如图,在 中,,,,动点 从点 出发沿射线 方向以 的速度运动.设运动的时间为 秒,则当 秒时, 为直角三角形.
三、解答题
如图所示,在 中, 于 ,,,.
(1) 求 的长;
(2) 求证: 是直角三角形.
如图,, 两个村子在笔直河岸的同侧,, 两村到河岸的距离分别为 ,,,现在要在河岸 上建一水厂 向 , 两村输送自来水,要求 , 两村到水厂 的距离相等.
(1) 在图中作出水厂 的位置(要求:尺规作图,不写作法,保留作图痕迹).
(2) 求水厂 距离 处多远?
如图,某人欲横渡一条河,由于水流的影响,实际上岸地点 与欲到达地点 相距 米,结果他在水中实际行走的路程比河的宽度多 米,求该河的宽度 .
如图,已知四边形 中,,,,,,则四边 的面积是多少?
如图,一架 长的梯子 斜靠在一竖直墙 上,这时 为 .
(1) 求 的长度.
(2) 如果梯子底端 沿地面向外移动 到达点 后停在 的位置上,那么梯子顶端 下移多少?
《直指算法统宗》中有一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地,送行二步与人齐,五尺人高曾记 ”翻译成现代文为:如图所示,秋千绳索 悬挂于 点,静止时竖直下垂, 点为踏板位置,踏板离地高度为一尺( 尺).将它往前推进 尺( 于点 ,且 尺, 尺为一步),踏板升高到点 的位置,此时踏板离地五尺( 尺),求秋千绳索( 或 )的长度.
如图, 中,,,点 为 边上的一个动点(不与点 , 及 中点重合),连接 ,点 关于直线 的对称点为点 ,直线 , 交于点 .
(1) 如图 ,当 时,根据题意将图形补充完整,并直接写出 的度数;
(2) 如图 ,当 时,用等式表示线段 ,, 之间的数量关系,并加以证明.
一、选择题
在 中,,, 的对边分别是 ,,,下列命题中的假命题是
A.若 ,则
B.若 ,则 不是直角三角形
C.若 ,则
D.若 ,则
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形 ,,, 的面积分别是 ,,,,则最大正方形 的边长是
A. B. C. D.无法确定
五根小木棒,其长度分别为 ,,,,,现将它们摆成各选项所示的两个直角三角形,其中正确的是
A. B.
C. D.
如图,将两个大小、形状完全相同的 和 拼在一起,其中点 与点 重合,点 落在边 上,连接 .若 ,,则 的长为
A. B. C. D.
如图是一连串直角三角形演化而成的.其中 ,记 ,,, 为相应三角形的面积.则 ( 为正整数)的值为
A. B. C. D.
我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若 ,,则该矩形的面积为
A. B. C. D.
已知三角形三边长为 ,,,如果 ,则该三角形是
A.以 为斜边的直角三角形 B.以 为斜边的直角三角形
C.以 为斜边的直角三角形 D.不是直角三角形
如图,在四边形 中,,,,.分别以点 , 为圆心,大于 的长为半径作弧,两弧交于点 ,作射线 交 于点 ,交 于点 .若 是 的中点,则 的长为
A. B. C. D.
二、填空题
把两个同样大小的含 角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点 ,且另三个锐角顶点 ,, 在同一直线上.若 ,则 .
如图,有一块田地的形状和尺寸如图所示,则它的面积为 .
如图,有一棱长为 的正方体盒子,现要按图中箭头所指方向从点 到点 拉一条捆绑线绳,使线绳经过 ,,, 四个面,则所需捆绑线绳的长至少为 .
如图,在 中,,,过点 作 ,连接 ,,过点 作 于点 ,若 , 的面积为 ,则 的长为 .
如图,已知直角三角形 中, 为直角,,,三角形 为等腰三角形,其中 ,且 , 为 中点,连接 ,,,则三角形 的面积为 .
如图,在 中,,,,动点 从点 出发沿射线 方向以 的速度运动.设运动的时间为 秒,则当 秒时, 为直角三角形.
三、解答题
如图所示,在 中, 于 ,,,.
(1) 求 的长;
(2) 求证: 是直角三角形.
如图,, 两个村子在笔直河岸的同侧,, 两村到河岸的距离分别为 ,,,现在要在河岸 上建一水厂 向 , 两村输送自来水,要求 , 两村到水厂 的距离相等.
(1) 在图中作出水厂 的位置(要求:尺规作图,不写作法,保留作图痕迹).
(2) 求水厂 距离 处多远?
如图,某人欲横渡一条河,由于水流的影响,实际上岸地点 与欲到达地点 相距 米,结果他在水中实际行走的路程比河的宽度多 米,求该河的宽度 .
如图,已知四边形 中,,,,,,则四边 的面积是多少?
如图,一架 长的梯子 斜靠在一竖直墙 上,这时 为 .
(1) 求 的长度.
(2) 如果梯子底端 沿地面向外移动 到达点 后停在 的位置上,那么梯子顶端 下移多少?
《直指算法统宗》中有一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地,送行二步与人齐,五尺人高曾记 ”翻译成现代文为:如图所示,秋千绳索 悬挂于 点,静止时竖直下垂, 点为踏板位置,踏板离地高度为一尺( 尺).将它往前推进 尺( 于点 ,且 尺, 尺为一步),踏板升高到点 的位置,此时踏板离地五尺( 尺),求秋千绳索( 或 )的长度.
如图, 中,,,点 为 边上的一个动点(不与点 , 及 中点重合),连接 ,点 关于直线 的对称点为点 ,直线 , 交于点 .
(1) 如图 ,当 时,根据题意将图形补充完整,并直接写出 的度数;
(2) 如图 ,当 时,用等式表示线段 ,, 之间的数量关系,并加以证明.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
