23.2.2中心对称图形 导学案(含答案)2023-2024学年度人教版九年级数学上册
文档属性
| 名称 | 23.2.2中心对称图形 导学案(含答案)2023-2024学年度人教版九年级数学上册 |

|
|
| 格式 | doc | ||
| 文件大小 | 305.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-23 17:43:48 | ||
图片预览

文档简介
23.2.2 中心对称图形
学习目标
1.经历观察图形的过程,建立中心对称图形的概念,会判断一个图形是不是中心对称图形.
2.通过动手操作,总结找中心对称图形 对称中心的方法,发展归纳、总结的能 力,积累问题的能力.
重点:中心对称图形的概念及其他运用
难点:中心对称图形性质的灵活运用
学习过程
一、创设问题情境
观察如图所示的三个图形,你能发现什么?与同伴交流你的看法.
二、自主学习
自学教材66-67页内容并思考:
1.线段绕其中点旋转180°后,与其自身 重合 ;平行四边形绕对角线交点旋转180°后,与其自身 重合 .你还能再举出一个类似的图形吗
答案不唯一,如正方形、菱形、圆等.
2.在下列几个图案中,绕某一点旋转180°后能与其自身重合的是 ①④ .
3.线段的对称中心是它的 中点 ,平行四边形的对称中心是 对角线的交点 .回忆中心对称中对称中心的找法,如何确定一个中心对称图形的对称中心
任意两对对应点连线的交点即为对称中心.
三、揭示问题规律
1.把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
2.中心对称和中心对称图形有什么区别和联系
区别 联系
中心对称 中心对称指 两 个图形之间的关系 把中心对称的两个图形看成一个“整体”,则成为 中心对称图形 ,把中心对称图形的两部分看作“两个图形”,则它们成 中心对称
中心对称图形 中心对称图形是指具有某种特征的 一 个图形
四、尝试应用
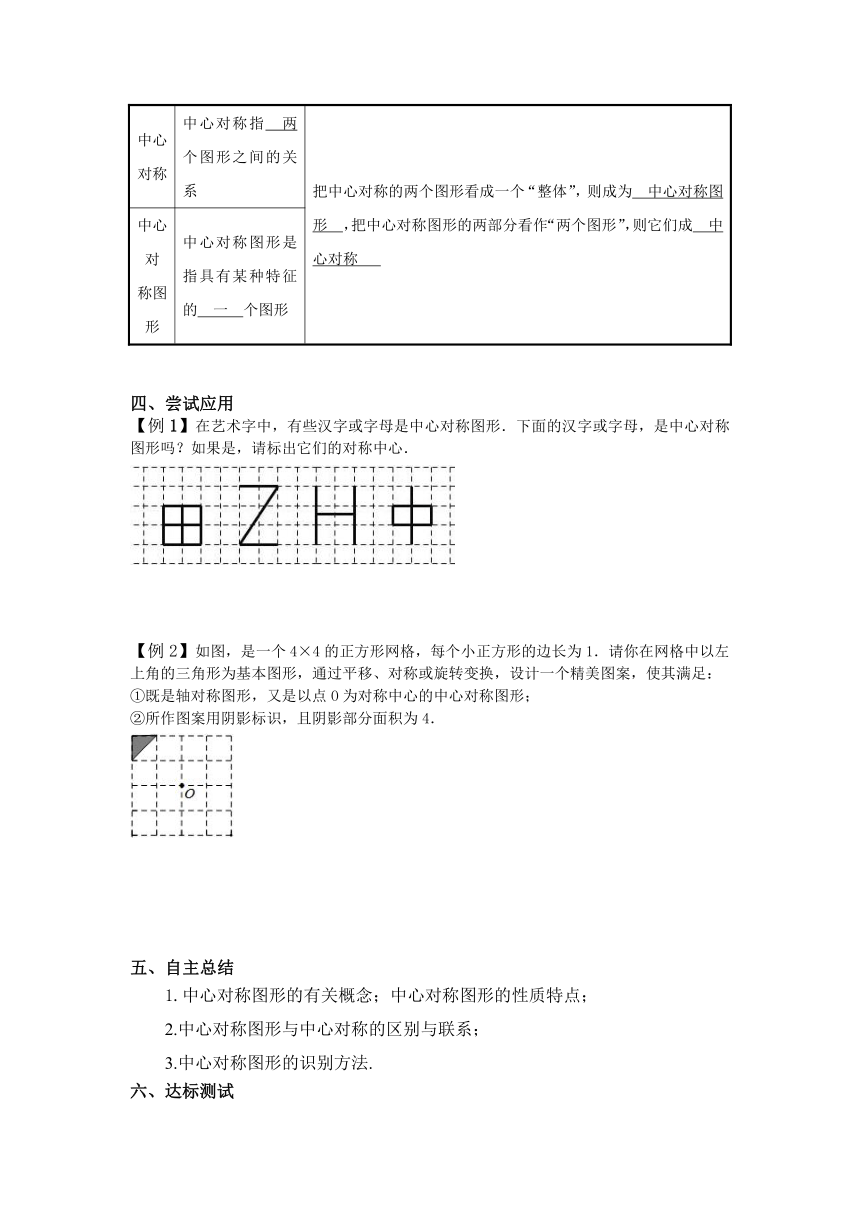
【例1】在艺术字中,有些汉字或字母是中心对称图形.下面的汉字或字母,是中心对称图形吗?如果是,请标出它们的对称中心.
【例2】如图,是一个4×4的正方形网格,每个小正方形的边长为1.请你在网格中以左上角的三角形为基本图形,通过平移、对称或旋转变换,设计一个精美图案,使其满足:
①既是轴对称图形,又是以点O为对称中心的中心对称图形;
②所作图案用阴影标识,且阴影部分面积为4.
五、自主总结
1.中心对称图形的有关概念;中心对称图形的性质特点;
2.中心对称图形与中心对称的区别与联系;
3.中心对称图形的识别方法.
达标测试
一、选择题
1.下面图形中,是中心对称图形的是( )
A. B.C. D.
2.在正方形、等腰三角形、矩形、菱形中,既是中心对称图形又是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
3.将两个全等的直角三角形纸片构成如图的四个图形,其中属于中心对称图形的是( )
A.A B.B C.C D.D
4.把等腰△ABC沿底边BC翻折,得到△DBC,那么四边形ABDC( )
A.是中心对称图形,不是轴对称图形B.是轴对称图形,不是中心对称图形
C.既是中心对称图形,又是轴对称图形D.以上都不正确
二、填空题
5.下列四个汽车图标中,既是中心对称图形又是轴对称图形的图标有______个.
6.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有_______种.
三、解答题
7.如图,AC=BD,∠A=∠B,点E,F在AB上,且DE∥CF,试说明该图是中心对称图形.
8.阅读材料:对于中心对称图形,过对称中心的任意一条直线都把这个图形的面积分成相等的两部分,如图:
尝试应用:(1)将图1分成面积相等的两部分(不写作法,保留作图痕迹):
(2)用不同的方法把图2分成面积相等的两部分:
拓展延伸:把图3分成面积相等的两部分.
23.2.2 中心对称图形
1.C 解析:选项A、不是中心对称图形,错误;选项B、不是中心对称图形,错误;选项C、是中心对称图形,正确;选项D、不是中心对称图形,错误.
2.C 解析:中心对称图形有正方形、矩形、菱形;轴对称图形有:正方形、等腰梯形、矩形、菱形,既是中心对称又是轴对称的图形有正方形、矩形、菱形.
3.C解析:A、不是中心对称图形,故此选项错误;B、不是中心对称图形,故此选项错误;C、是中心对称图形,故此选项正确;D、不是中心对称图形,故此选项错误;故选C.
4.C 解析:∵等腰△ABC沿底边BC翻折,得到△DBC,∴四边形ABDC是菱形,∵菱形既是中心对称图形,又是轴对称图形,∴四边形ABDC既是中心对称图形,又是轴对称图形.
5.1 解析:第一个图不是轴对称图形,不是中心对称图形,故不合题意;第二个图形是中心对称图形,也是轴对称图形,故符合题意;第三个图形不是中心对称图形,是轴对称图形,故不合题意;第四个图形不是中心对称图形,是轴对称图形,故不合题意.
6.4 解析:如图所示:这个格点正方形的作法共有4种.
7.连接CD交AB于点O,∵AC=BD,∠A=∠B,又∵∠AOC=∠BOD, ∴△ACO≌△BDO(AAS) ∴OA=OB,OC=OD,∴A,B和C,D分别关于点O对称. ∵DE∥CF,∴∠ODE=∠OCF,又∵∠DOE=∠COF,OC=OD, ∴△ODE≌△OCF(ASA) ∴OE=OF,∴点E,F也关于点O对称,∴此图形是中心对称图形,对称中心是点O.
8.解:尝试应用(1)
(2)
拓展延伸:
学习目标
1.经历观察图形的过程,建立中心对称图形的概念,会判断一个图形是不是中心对称图形.
2.通过动手操作,总结找中心对称图形 对称中心的方法,发展归纳、总结的能 力,积累问题的能力.
重点:中心对称图形的概念及其他运用
难点:中心对称图形性质的灵活运用
学习过程
一、创设问题情境
观察如图所示的三个图形,你能发现什么?与同伴交流你的看法.
二、自主学习
自学教材66-67页内容并思考:
1.线段绕其中点旋转180°后,与其自身 重合 ;平行四边形绕对角线交点旋转180°后,与其自身 重合 .你还能再举出一个类似的图形吗
答案不唯一,如正方形、菱形、圆等.
2.在下列几个图案中,绕某一点旋转180°后能与其自身重合的是 ①④ .
3.线段的对称中心是它的 中点 ,平行四边形的对称中心是 对角线的交点 .回忆中心对称中对称中心的找法,如何确定一个中心对称图形的对称中心
任意两对对应点连线的交点即为对称中心.
三、揭示问题规律
1.把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
2.中心对称和中心对称图形有什么区别和联系
区别 联系
中心对称 中心对称指 两 个图形之间的关系 把中心对称的两个图形看成一个“整体”,则成为 中心对称图形 ,把中心对称图形的两部分看作“两个图形”,则它们成 中心对称
中心对称图形 中心对称图形是指具有某种特征的 一 个图形
四、尝试应用
【例1】在艺术字中,有些汉字或字母是中心对称图形.下面的汉字或字母,是中心对称图形吗?如果是,请标出它们的对称中心.
【例2】如图,是一个4×4的正方形网格,每个小正方形的边长为1.请你在网格中以左上角的三角形为基本图形,通过平移、对称或旋转变换,设计一个精美图案,使其满足:
①既是轴对称图形,又是以点O为对称中心的中心对称图形;
②所作图案用阴影标识,且阴影部分面积为4.
五、自主总结
1.中心对称图形的有关概念;中心对称图形的性质特点;
2.中心对称图形与中心对称的区别与联系;
3.中心对称图形的识别方法.
达标测试
一、选择题
1.下面图形中,是中心对称图形的是( )
A. B.C. D.
2.在正方形、等腰三角形、矩形、菱形中,既是中心对称图形又是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
3.将两个全等的直角三角形纸片构成如图的四个图形,其中属于中心对称图形的是( )
A.A B.B C.C D.D
4.把等腰△ABC沿底边BC翻折,得到△DBC,那么四边形ABDC( )
A.是中心对称图形,不是轴对称图形B.是轴对称图形,不是中心对称图形
C.既是中心对称图形,又是轴对称图形D.以上都不正确
二、填空题
5.下列四个汽车图标中,既是中心对称图形又是轴对称图形的图标有______个.
6.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有_______种.
三、解答题
7.如图,AC=BD,∠A=∠B,点E,F在AB上,且DE∥CF,试说明该图是中心对称图形.
8.阅读材料:对于中心对称图形,过对称中心的任意一条直线都把这个图形的面积分成相等的两部分,如图:
尝试应用:(1)将图1分成面积相等的两部分(不写作法,保留作图痕迹):
(2)用不同的方法把图2分成面积相等的两部分:
拓展延伸:把图3分成面积相等的两部分.
23.2.2 中心对称图形
1.C 解析:选项A、不是中心对称图形,错误;选项B、不是中心对称图形,错误;选项C、是中心对称图形,正确;选项D、不是中心对称图形,错误.
2.C 解析:中心对称图形有正方形、矩形、菱形;轴对称图形有:正方形、等腰梯形、矩形、菱形,既是中心对称又是轴对称的图形有正方形、矩形、菱形.
3.C解析:A、不是中心对称图形,故此选项错误;B、不是中心对称图形,故此选项错误;C、是中心对称图形,故此选项正确;D、不是中心对称图形,故此选项错误;故选C.
4.C 解析:∵等腰△ABC沿底边BC翻折,得到△DBC,∴四边形ABDC是菱形,∵菱形既是中心对称图形,又是轴对称图形,∴四边形ABDC既是中心对称图形,又是轴对称图形.
5.1 解析:第一个图不是轴对称图形,不是中心对称图形,故不合题意;第二个图形是中心对称图形,也是轴对称图形,故符合题意;第三个图形不是中心对称图形,是轴对称图形,故不合题意;第四个图形不是中心对称图形,是轴对称图形,故不合题意.
6.4 解析:如图所示:这个格点正方形的作法共有4种.
7.连接CD交AB于点O,∵AC=BD,∠A=∠B,又∵∠AOC=∠BOD, ∴△ACO≌△BDO(AAS) ∴OA=OB,OC=OD,∴A,B和C,D分别关于点O对称. ∵DE∥CF,∴∠ODE=∠OCF,又∵∠DOE=∠COF,OC=OD, ∴△ODE≌△OCF(ASA) ∴OE=OF,∴点E,F也关于点O对称,∴此图形是中心对称图形,对称中心是点O.
8.解:尝试应用(1)
(2)
拓展延伸:
同课章节目录
