24.1.3弧、弦、圆心角导学案 (含答案)2023-2024学年度人教版九年级数学上册
文档属性
| 名称 | 24.1.3弧、弦、圆心角导学案 (含答案)2023-2024学年度人教版九年级数学上册 |  | |
| 格式 | doc | ||
| 文件大小 | 239.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-23 17:44:30 | ||
图片预览

文档简介
24.1.3 弧、弦、圆心角
学习目标
1.理解圆心角的概念,并能够准确辨认圆心角所对的弧和弦.
2.利用圆的中心对称性,研究圆心角、弧、弦之间的关系,能利用圆心角、弧、弦之间的关系解决有关的证明与计算问题.
重点:探索圆心角、弧、弦之间关系定理并利用其解决相关问题.
难点:理解圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的意义.
学习过程
一、创设问题情境
问题 1.圆是轴对称图形,其对称轴是_______________.圆还是_________对称图形,其对称中心是____________.
2.圆绕____________旋转____________度可以与自身重合,由此可得:圆具有旋转不变性.
1.过圆心的直线 中心对称图圆心 形 2.圆心 任意角度
二、自主学习
自学教材59页内容并思考:
1、由圆的旋转不变性可得到什么结论;
2、圆心角的概念,探究弧、弦、圆心角三者之间的关系并能运用定理解题.
三、揭示问题规律
1.圆心角:顶点在____________的角,叫圆心角.
圆心
2.探究:
(1)如图,☉O中∠AOB=∠A'OB',则AB________A'B', _______.
(2)如图,☉O中=,则∠AOB_______∠A'OB',AB_______A'B'.
(3)如图,☉O中AB=A'B',则∠AOB_______∠A'OB', ________.
(1) = = (2)= = (3)= =
文字语言叙述:
在同圆或等圆中,相等的圆心角所对的弧____________,所对的弦也____________.
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角____________,所对的弦____________.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角____________,所对的弧____________.
符号语言:如上图
∵∠AOB=∠A'OB', ∴____________,____________.
(2)∵=, ∴____________,____________;
(3)∵AB=A'B', ∴____________,____________.
相 等 相 等
相 等 相 等
相 等 相 等
(1)AB=A'B' = (2)∠AOB=∠A'OB' AB=A'B' (3) = ∠AOB=∠A'OB'
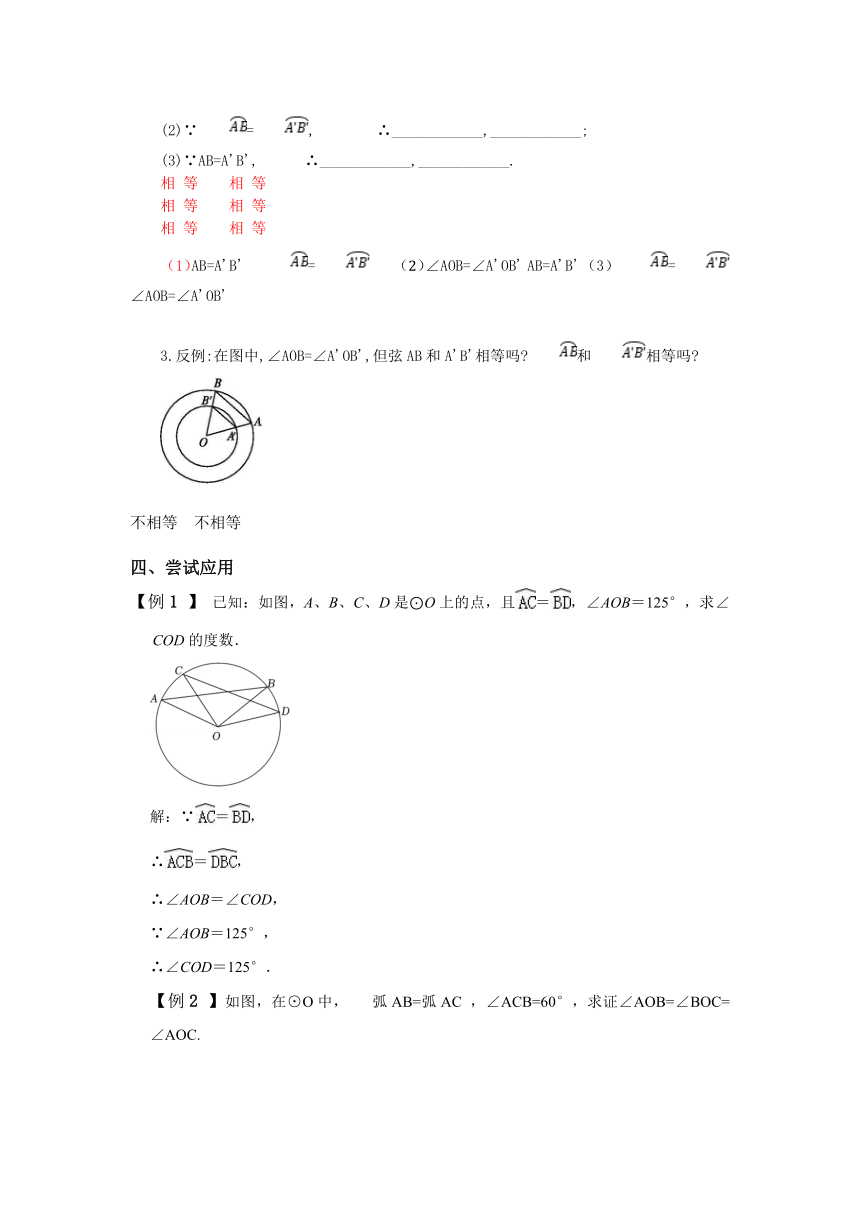
3.反例:在图中,∠AOB=∠A'OB',但弦AB和A'B'相等吗 和相等吗
不相等 不相等
四、尝试应用
【例1 】 已知:如图,A、B、C、D是⊙O上的点,且=,∠AOB=125°,求∠COD的度数.
解:∵=,
∴=,
∴∠AOB=∠COD,
∵∠AOB=125°,
∴∠COD=125°.
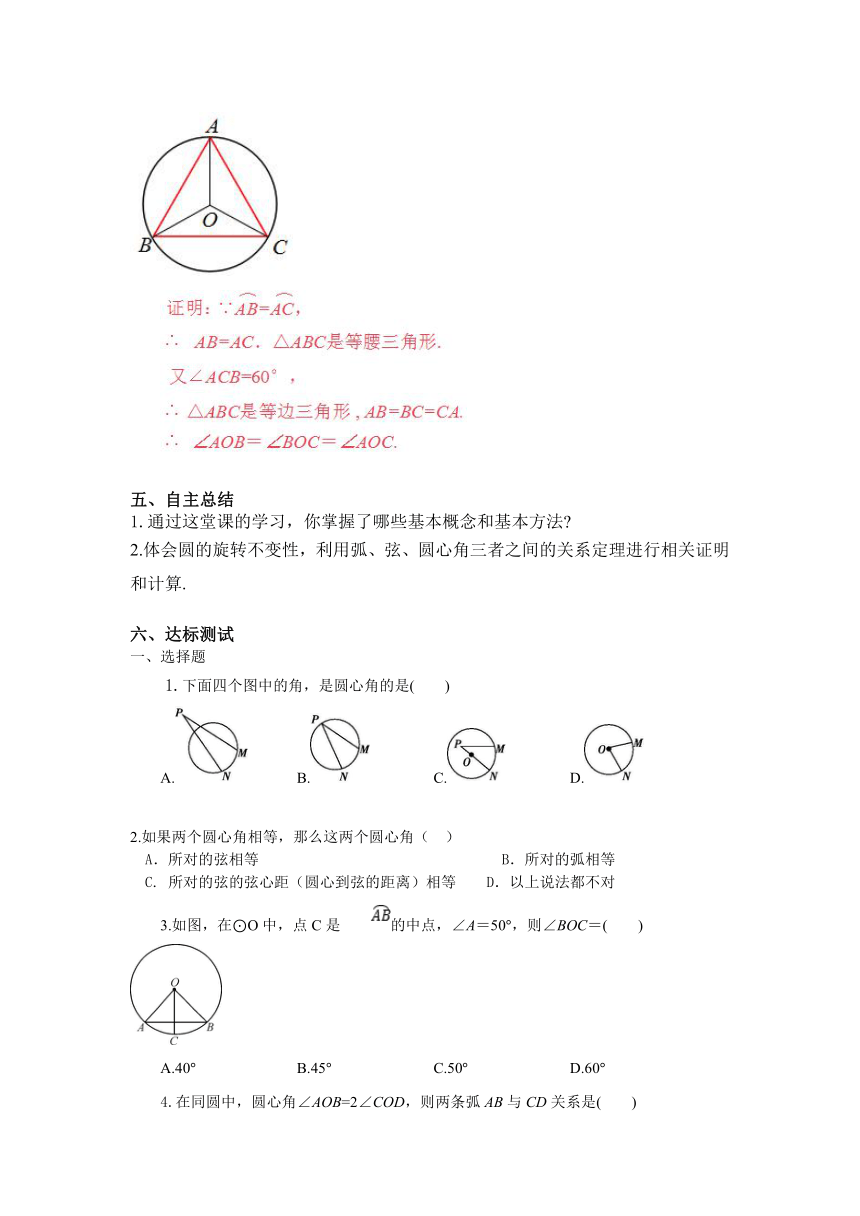
【例2 】如图,在⊙O中, 弧AB=弧AC ,∠ACB=60°,求证∠AOB=∠BOC=∠AOC.
五、自主总结
1.通过这堂课的学习,你掌握了哪些基本概念和基本方法
2.体会圆的旋转不变性,利用弧、弦、圆心角三者之间的关系定理进行相关证明和计算.
达标测试
一、选择题
1.下面四个图中的角,是圆心角的是( )
A. B. C. D.
2.如果两个圆心角相等,那么这两个圆心角( )
A.所对的弦相等 B.所对的弧相等
C. 所对的弦的弦心距(圆心到弦的距离)相等 D.以上说法都不对
3.如图,在⊙O中,点C是的中点,∠A=50°,则∠BOC=( )
A.40° B.45° C.50° D.60°
4.在同圆中,圆心角∠AOB=2∠COD,则两条弧AB与CD关系是( )
A.弧AB=2弧CD B.弧AB<2弧CD
C.弧AB>2弧CD D.不能确定
5.如图,已知⊙O的半径等于1cm,AB是直径,C,D是⊙O上的两点,且==,则四边形ABCD的周长等于( )
A.4cm B.5cm C.6cm D.7cm
二、填空题
6.如图,AB是⊙O的直径,AC、CD、DE、EF、FB都是⊙O的弦,且AC=CD=DE=EF=FB,则∠AOC= .
7.如图,已知AB、CD是⊙O的直径,=,∠BOD=32°,则∠COE的度数为 度.
8.如图,AB,CD是⊙O的两条弦,M,N分别为AB,CD的中点,且∠AMN=∠CNM,AB=6,则CD= .
24.1.3 弧、弦、圆心角关系定理
1.D 2.D
3.A【解析】△OAB中,OA=OB,∴∠BOA=180°-2∠A=80°;
∵点C是的中点,即,∴∠BOC=∠BOA=40°.
4.C【解析】在∠AOB中取弧AB的中点E,那么∠AOE=∠BOE==∠COD,
考虑到同样大小的圆心角对应的弦是相等的,所以AE=BE=CD,
在△ABE中,两边之和大于第三边,所以AE+BE=2CD>AB.
5.B【解析】如图,连接OD、OC.
∵==(已知),
∴∠AOD=∠DOC=∠COB(在同圆中,等弧所对的圆心角相等);
∵AB是直径,
∴∠AOD+∠DOC+∠COB=180°,
∴∠AOD=∠DOC=∠COB=60°;
∵OA=OD(⊙O的半径),
∴△AOD是等边三角形,
∴AD=OD=OA;
同理,得
OC=OD=CD,OC=OB=BC,
∴AD=CD=BC=OA,
∴四边形ABCD的周长为:AD+CD+BC+AB=5OA=5×1cm=5cm;故选:B.
6. 36°【解析】∵AC=CD=DF=EF=FB,
∴∠AOC=∠COD=∠DOE=∠EOF=∠BOF,
∵AB是⊙O的直径,
∴∠AOB=180°,
∴∠AOC=∠AOB=36°.
7. 64【解析】∵∠BOD=32°,
∴∠AOC=∠BOD=32°,
∵=,
∴∠AOE=∠AOC=32°,
∴∠COE=∠AOC+∠AOE=32°+32°=64°.
8. 6 解析:连接OM,ON,OA,OC,
∵M、N分别为AB、CD的中点,
∴OM⊥AB,ON⊥CD,
∴AM=AB,CN=CD,
∵∠AMN=∠CNM,
∴∠NMO=∠MNO,即OM=ON,
在Rt△AOM与Rt△CON中,,
∴Rt△AOM≌Rt△CON(HL),
∴AM=CN,
∴AB=CD=6.
学习目标
1.理解圆心角的概念,并能够准确辨认圆心角所对的弧和弦.
2.利用圆的中心对称性,研究圆心角、弧、弦之间的关系,能利用圆心角、弧、弦之间的关系解决有关的证明与计算问题.
重点:探索圆心角、弧、弦之间关系定理并利用其解决相关问题.
难点:理解圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的意义.
学习过程
一、创设问题情境
问题 1.圆是轴对称图形,其对称轴是_______________.圆还是_________对称图形,其对称中心是____________.
2.圆绕____________旋转____________度可以与自身重合,由此可得:圆具有旋转不变性.
1.过圆心的直线 中心对称图圆心 形 2.圆心 任意角度
二、自主学习
自学教材59页内容并思考:
1、由圆的旋转不变性可得到什么结论;
2、圆心角的概念,探究弧、弦、圆心角三者之间的关系并能运用定理解题.
三、揭示问题规律
1.圆心角:顶点在____________的角,叫圆心角.
圆心
2.探究:
(1)如图,☉O中∠AOB=∠A'OB',则AB________A'B', _______.
(2)如图,☉O中=,则∠AOB_______∠A'OB',AB_______A'B'.
(3)如图,☉O中AB=A'B',则∠AOB_______∠A'OB', ________.
(1) = = (2)= = (3)= =
文字语言叙述:
在同圆或等圆中,相等的圆心角所对的弧____________,所对的弦也____________.
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角____________,所对的弦____________.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角____________,所对的弧____________.
符号语言:如上图
∵∠AOB=∠A'OB', ∴____________,____________.
(2)∵=, ∴____________,____________;
(3)∵AB=A'B', ∴____________,____________.
相 等 相 等
相 等 相 等
相 等 相 等
(1)AB=A'B' = (2)∠AOB=∠A'OB' AB=A'B' (3) = ∠AOB=∠A'OB'
3.反例:在图中,∠AOB=∠A'OB',但弦AB和A'B'相等吗 和相等吗
不相等 不相等
四、尝试应用
【例1 】 已知:如图,A、B、C、D是⊙O上的点,且=,∠AOB=125°,求∠COD的度数.
解:∵=,
∴=,
∴∠AOB=∠COD,
∵∠AOB=125°,
∴∠COD=125°.
【例2 】如图,在⊙O中, 弧AB=弧AC ,∠ACB=60°,求证∠AOB=∠BOC=∠AOC.
五、自主总结
1.通过这堂课的学习,你掌握了哪些基本概念和基本方法
2.体会圆的旋转不变性,利用弧、弦、圆心角三者之间的关系定理进行相关证明和计算.
达标测试
一、选择题
1.下面四个图中的角,是圆心角的是( )
A. B. C. D.
2.如果两个圆心角相等,那么这两个圆心角( )
A.所对的弦相等 B.所对的弧相等
C. 所对的弦的弦心距(圆心到弦的距离)相等 D.以上说法都不对
3.如图,在⊙O中,点C是的中点,∠A=50°,则∠BOC=( )
A.40° B.45° C.50° D.60°
4.在同圆中,圆心角∠AOB=2∠COD,则两条弧AB与CD关系是( )
A.弧AB=2弧CD B.弧AB<2弧CD
C.弧AB>2弧CD D.不能确定
5.如图,已知⊙O的半径等于1cm,AB是直径,C,D是⊙O上的两点,且==,则四边形ABCD的周长等于( )
A.4cm B.5cm C.6cm D.7cm
二、填空题
6.如图,AB是⊙O的直径,AC、CD、DE、EF、FB都是⊙O的弦,且AC=CD=DE=EF=FB,则∠AOC= .
7.如图,已知AB、CD是⊙O的直径,=,∠BOD=32°,则∠COE的度数为 度.
8.如图,AB,CD是⊙O的两条弦,M,N分别为AB,CD的中点,且∠AMN=∠CNM,AB=6,则CD= .
24.1.3 弧、弦、圆心角关系定理
1.D 2.D
3.A【解析】△OAB中,OA=OB,∴∠BOA=180°-2∠A=80°;
∵点C是的中点,即,∴∠BOC=∠BOA=40°.
4.C【解析】在∠AOB中取弧AB的中点E,那么∠AOE=∠BOE==∠COD,
考虑到同样大小的圆心角对应的弦是相等的,所以AE=BE=CD,
在△ABE中,两边之和大于第三边,所以AE+BE=2CD>AB.
5.B【解析】如图,连接OD、OC.
∵==(已知),
∴∠AOD=∠DOC=∠COB(在同圆中,等弧所对的圆心角相等);
∵AB是直径,
∴∠AOD+∠DOC+∠COB=180°,
∴∠AOD=∠DOC=∠COB=60°;
∵OA=OD(⊙O的半径),
∴△AOD是等边三角形,
∴AD=OD=OA;
同理,得
OC=OD=CD,OC=OB=BC,
∴AD=CD=BC=OA,
∴四边形ABCD的周长为:AD+CD+BC+AB=5OA=5×1cm=5cm;故选:B.
6. 36°【解析】∵AC=CD=DF=EF=FB,
∴∠AOC=∠COD=∠DOE=∠EOF=∠BOF,
∵AB是⊙O的直径,
∴∠AOB=180°,
∴∠AOC=∠AOB=36°.
7. 64【解析】∵∠BOD=32°,
∴∠AOC=∠BOD=32°,
∵=,
∴∠AOE=∠AOC=32°,
∴∠COE=∠AOC+∠AOE=32°+32°=64°.
8. 6 解析:连接OM,ON,OA,OC,
∵M、N分别为AB、CD的中点,
∴OM⊥AB,ON⊥CD,
∴AM=AB,CN=CD,
∵∠AMN=∠CNM,
∴∠NMO=∠MNO,即OM=ON,
在Rt△AOM与Rt△CON中,,
∴Rt△AOM≌Rt△CON(HL),
∴AM=CN,
∴AB=CD=6.
同课章节目录
