第9章 变量之间的关系复习课件

课件34张PPT。第九章 复习与回顾1、能熟练找出自变量与因变量，并能理解、掌握自变量与因变量之间的关系；
2、学会运用变量之间关系的三种表示方法分析变量之间的关系；
3、能从运动变化的角度解释生活中的数学现象，体验成就感，获得学习的快乐，发展对数学更高层次的认识。 学习目标
1、树上落下的果子的高度随时间的变化而变化，这里时间是 ，果子的高度是 。
2、小明骑自行车的速度是10km/小时，那么小明骑车所走的路程随时间的变化而变化,这里自变量是 ，因变量是 。
自变量因变量时间所走的路程导学13、（ ）引起（ ）的变化；
4、（ ）因（ ）的变化而变化；
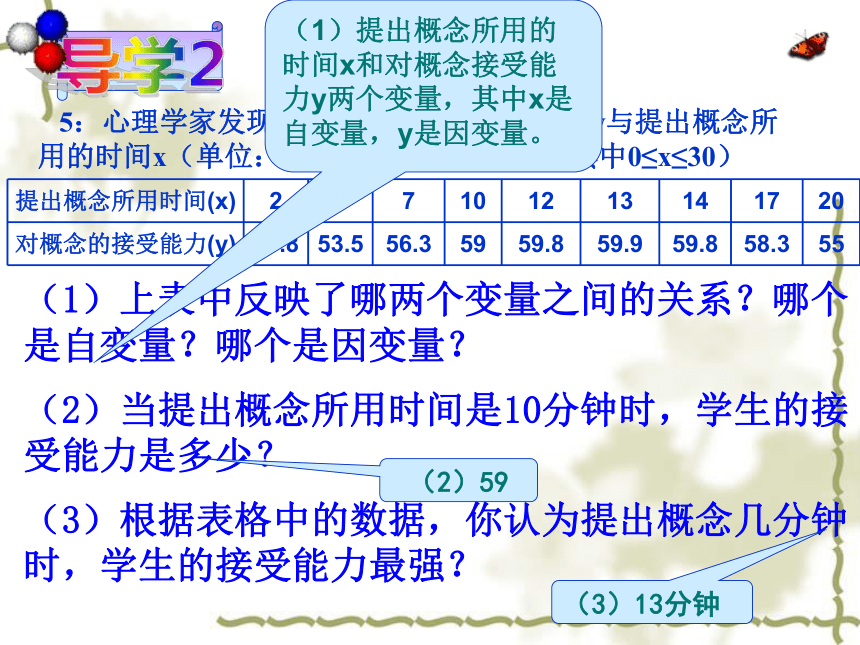
自变量因变量自变量因变量自变量与因变量之间的关系： 5：心理学家发现，学生对概念的接受能力y与提出概念所用的时间x（单位：分）之间有如下关系（其中0≤x≤30）（1）上表中反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
（2）当提出概念所用时间是10分钟时，学生的接受能力是多少？
（3）根据表格中的数据，你认为提出概念几分钟时，学生的接受能力最强？导学2（1）提出概念所用的时间x和对概念接受能力y两个变量，其中x是自变量，y是因变量。
（2）59（3）13分钟
5：心理学家发现，学生对概念的接受能力y与提出概念所用的时间x（单位：分）之间有如下关系（其中0≤x≤30）（4）从表格中可知，当时间x在什么范围内，学生的接受能力逐步增强？当时间x在什么范围内，学生的接受能力逐步降低？
(5) 根据表格大致估计当时间为23分钟时，学生对概念的接受能力是多少。导学22分钟至13分钟13分钟至20分钟
6.一名同学在用弹簧做实验，在弹簧上挂不同质量的物体后，弹簧的长度就会发生变化，实验数据如下表：
(1)上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？(2)弹簧不挂物体时的长度是多少？如果用x表示弹性限度内物体的质量，用y表示弹簧的长度，那么随着x的变化，y的变化趋势如何？(3)如果此弹簧最大挂重量为15千克，你能预测当挂重为10千克时，弹簧的长度是多少？弹簧的长度能否达到20cm?所挂物体的质量和弹簧的长度；所挂物体的质量是因变量，弹簧的长度是因变量12cm;y=12+0.5x当所挂物体为10千克时，
y=12+0.5×10=17cm.最大承重量为15千克，所以最大长度为y=12+15×0.5=19.5cm,故不能达到20cm.1)、借助表格可以感知因变量随自变量变化的情况。
2)、从表格中可以获取一些信息，能作出某种预测或估计。表 格导学3 7、一长方形的长为5，宽为x，则这个长方形的面积y的关系式为 . 8、地球上某地区的温度T（℃）与高度h（m）的关系可近似地用公式T=100-0.15h来表示。如果h=200(m)，那么T的值等于（ 　 ）
　A、70 ℃ 　　　　　B、50 ℃
　Ｃ、１００ ℃ 　　Ｄ、２００ ℃ｙ＝５ｘＡ 9: 某蓄水池开始蓄水，每时进水20米3，设蓄水量为V（米3），蓄水时间为t（时）
（1）V与t之间的关系式是什么？
（2）当t从2变化到8时，相应的V值如何变化？
（3）若蓄水池最大蓄水量为1000米3，则需要多长时间能蓄满水？
（4）当t逐渐增加时，V怎样变化？说说你的理由。导学3V=20t
V值由40米3变化到160米3把V=1000米3代入关系式，得1000=20t，解 得 t=50(时）。当t逐渐增加时，V也在逐渐增加，因为V是t的正整数倍。
1、能根据题意列简单的关系式。
2、能利用关系式进行简单的计算。关 系 式1 1、我们熟知的龟兔赛跑的故事：骄傲的兔子比赛途中睡了一觉，结果输掉了比赛。能反映这场比赛中路程S与时间t的关系的是：S终点tB( )B导学4 12．分析下面反映变量之间关系的图像，想象一个适合它的实际情境.(1)可以把x和y分别代表时间和距离，那么这个图可以描述为：小华骑车从学校回家，一段时间后，停下来修车，然后又开始往家走，直到回家；

(2)可以把x和y分别代表时间和速度，那么这个图可以描述为：一辆汽车，减速行驶一段时间后，匀速行驶了一段时间，然后逐渐减速，到了目的地停下来.(3)可以把x和y分别代表时间和蓄水量，那么这个图可以描述为：一个水池先放水，一段时间后，停止，随后，又接着放水直到放完.(4) 可以把x和y分别代表时间和高度，那么这个图就可以描述为：一架飞机从一定的飞行高度慢慢下降一个高度，然后在这一高度飞行了一段时间后，快到机场时，开始降落，最后降落在机场.13、分析下图所反映的变量之间的关系，想象一个适合它的情境，并叙述出来。 14：一辆汽车以每小时50千米的速度行驶了t小时，行驶的路程为s千米. (1)这个情境中，有哪些变量？其中自变量是什么？因变量是什么？

(2)你能用哪种方式表示路程与时间之间的关系？具体做一做 。(3)该汽车行驶2.5小时的路程是多少千米？(4)一段公路全长350千米，这辆汽车行驶完全程需要多少小时？1)、识别图象是否正确。
2)、利用图象尽可能地获取自变量、因变量的信息。
图象水平方向的数轴（横轴）上的点竖直方向的数轴（纵轴）上的点 课堂小结本章内容你学到了多少？15、圆柱的底面圆的半径为10，当圆柱的高变化时圆柱的体积也随之变化．
（1）在这个变化过程中自变量是什么？因变量是什么？
（2）设圆柱的体积为V，圆柱的高为h，则V与h的关系式是什么？
（3）当h由2变化到4时，V是如何变化
的？ Ｖ＝πr h2课堂检测16、小明某天上午9时骑自行车离开家，15时回家，他有意描绘了离家的距离与时间的变化情况，如右图所示. （1）图象表示了哪两个
变量的关系？哪个是自
变量？哪个是因变量？
（2）10时和13时，他分
别离家多远？
（3）他到达离家最远的
地方是什么时间？离家
多远？
（4）11时到12时他行驶
了多少千米？
（5）他可能在哪段时间内休息，并吃午餐？
时间是自变量、距离是因变量15千米、30千米12时，离家30千米11千米12时到13时17、一只重10千克的仔猪，按平均每天增重0.7千克计算，求:
(1)这头猪的体重P（千克）与其饲养天数n之间的关系式．
(2)当饲养了20天时，这头猪的体重变为了多少？
(3)若这头猪的体重达到了17千克，此时它被饲养了多少天？
19.果子成熟从树上落到地面，它落下的高度与经过的时间有如下的关系：(1)上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？(2)如果果子经过2秒落到地上，那么请估计这果子开始落下时离地面的高度是多少米？(3)请你列出果子落下的高度h（米）与时间t（秒）之间的式 . .3．某种油箱容量为60升的汽车，加满汽油后，汽车行驶时油箱的油量Q（升）随汽车行驶时间t（时）变化的关系式如下：Q＝60－6t (1) 请完成下表(2)汽车行驶5小时后，油箱中油量是 升？(3)若汽车行驶过程中，油箱的油量为12升，则汽车行驶了 小时 ； (4)贮满60升汽油的汽车，最多行驶 时；3．某种油箱容量为60升的汽车，加满汽油后，汽车行驶时油箱的油量Q（升）随汽车行驶时间t（时）变化的关系式如下：Q＝60－6t (5)哪个图像能反映变量Q与t的关系:（ ） 1、书P209复习题1、2、3写在书上；
2、书P210数学理解部分第一题写在作业本上；作业布置谢谢指导！ 我们熟知的龟兔赛跑的故事：骄傲的兔子比赛途中睡了一觉，结果输掉了比赛。能反映这场比赛中路程S与时间t的关系的是：S终点tB( )B
知识回顾1．表示两个变量之间关系的方法有（　　）（　　）
　　（　　　）．　　　　　　　　　
２．图象法表示两个变量之间关系的特点是（　　　　）
３．用图象法表示两个变量之间关系时，通常用水平方向　　　　　　　　　　
　　的数轴（横轴）上的点表示（　　　），用竖直方向　　　
　　的数轴（纵轴）上的点表示（　　　）．因变量自变量关系式表格图象法非常直观4、利用变量之间的关系解决问题、进行预测例1: 某蓄水池开始蓄水，每时进水20米3，设蓄水量为V（米3），蓄水时间为t（时）
（1）V与t之间的关系式是什么？
（2）用表格表示当t从2变化到8时（每次增加1），相应的V值？
（3）若蓄水池最大蓄水量为1000米3，则需要多长时间能蓄满水？
（4）当t逐渐增加时，V怎样变化？说说你的理由。课堂检测：1.小红帮妈妈预算4月份的用电量，她记录了4月份初连续8天每天早上电表的读数，列成了表格如下：（1）这个表格反映哪两个变量之间的关系？哪个是 自变量？哪个是因变量？解：（1）这个表格反映日期与电表读数这两个量之间的关系，日期是自变量，电表读数是因变量。（2）4月5 日早上电表的读数是多少？（3）这个月的前5 天共用电多少？（小红家每天只在晚上用电）（3）39 － 21=18，即这个月的前5天共用电18千瓦时。（2）4月5日早上电表的读数是35千瓦时。