5.2 比较线段的长短课件

课件28张PPT。5.2比较线段的长短回顾思考：直线的特点、表示方法？
线段的特点、表示方法？
射线的特点、表示方法？
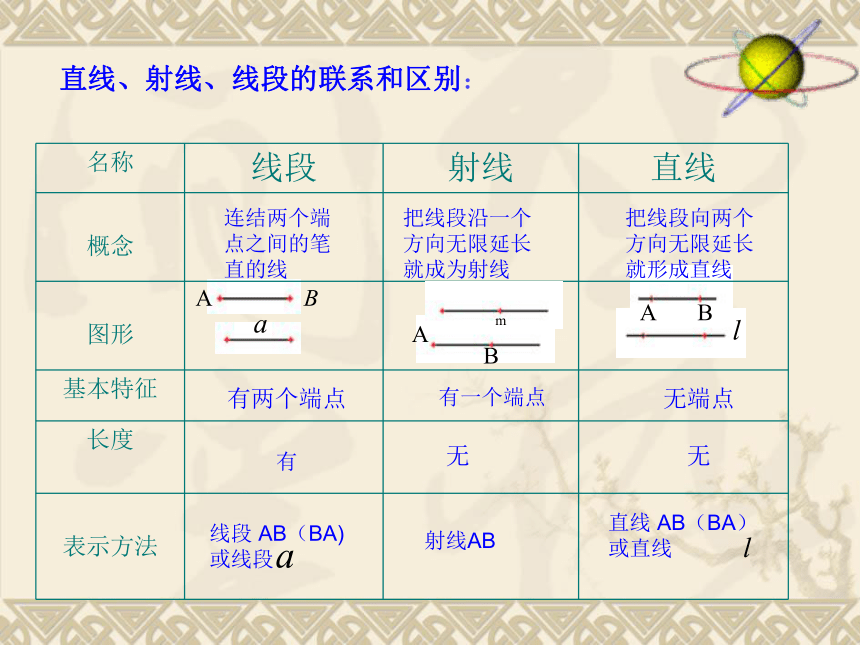
三者的区别和联系？直线、射线、线段的联系和区别：连结两个端点之间的笔直的线把线段沿一个方向无限延长就成为射线把线段向两个方向无限延长就形成直线有两个端点有一个端点无端点有无无线段 AB（BA)或线段射线AB直线 AB（BA）或直线想一想判断
1、延长直线MN到点C （ ）
2、直线A与直线B交于一点M （ ）
3、三点决定一条直线 （ ）
4、无数条直线可能交于一点 （ ）
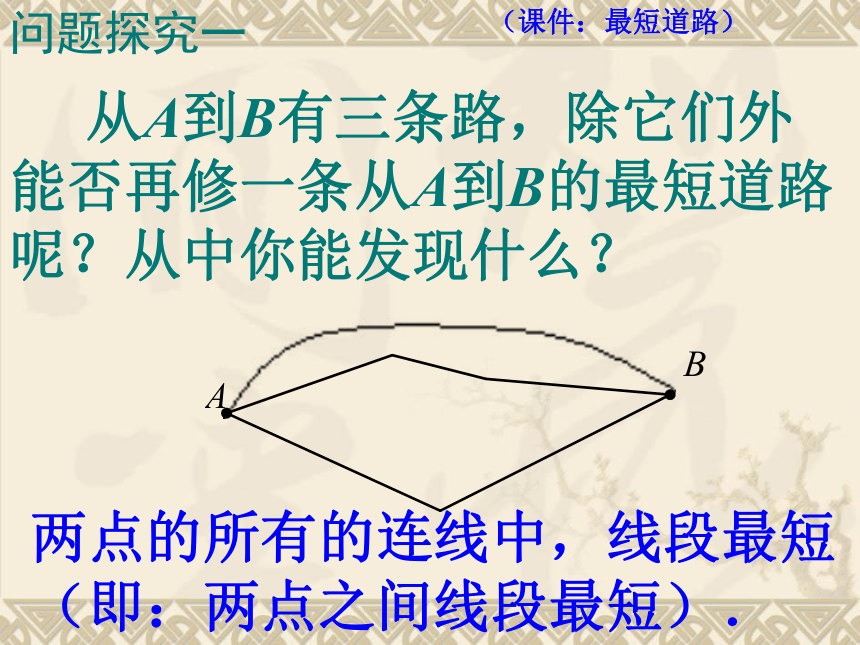
5、射线是直线的一半 （ ）错错错错对 从A到B有三条路，除它们外能否再修一条从A到B的最短道路呢？从中你能发现什么？ 问题探究一（课件：最短道路） 两点的所有的连线中，线段最短
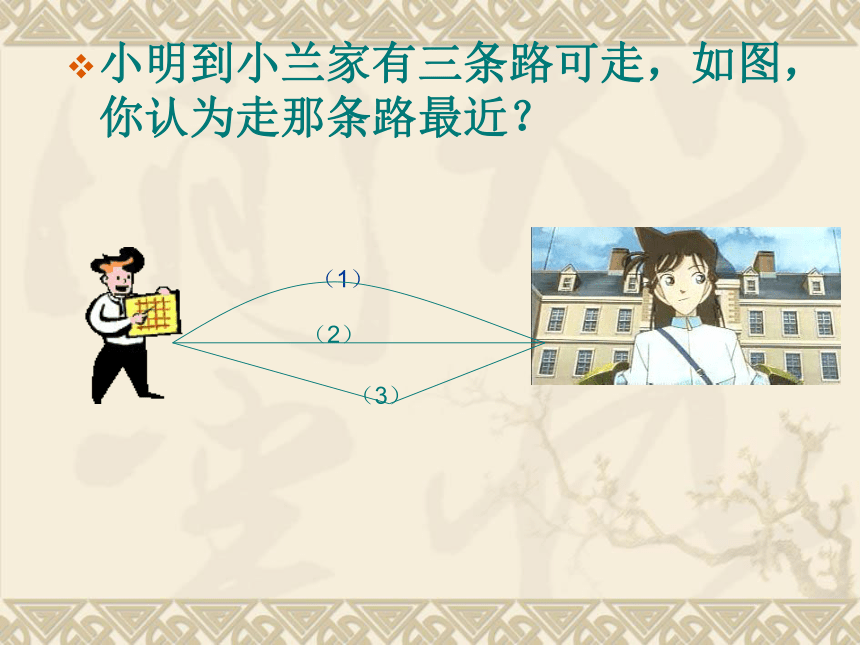
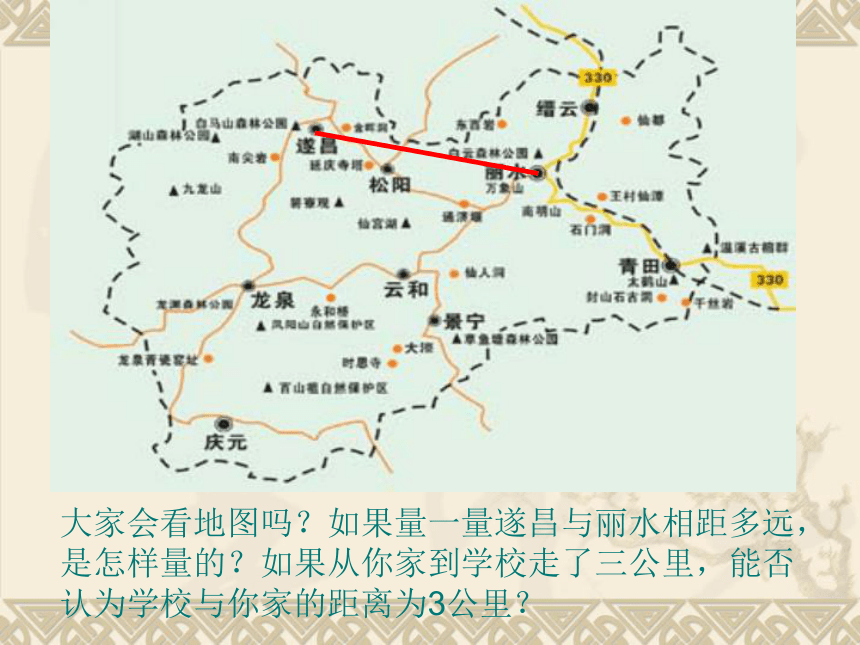
（即：两点之间线段最短）． 线段公理：两点之间的所有连线中，线段最短。想一想：在现实生活中，哪些时候运用了上述性质。两点之间线段最短。（1）小明到小兰家有三条路可走，如图，你认为走那条路最近？（2）（3）大家会看地图吗？如果量一量遂昌与丽水相距多远，是怎样量的？如果从你家到学校走了三公里，能否认为学校与你家的距离为3公里？2、两点之间线段的长度， 叫做这两点之间的距离。问题(1) 你如何比较两根筷子的长短？问题(3) 怎样比较两条线段的长短呢？问题(2) 两名同学如何比个儿？问题探究二线段的大小比较叠合法将线段重叠在一起，使一个端点重合，再进行比较.线段的长短比较ABCDAB = 0.8l 厘米CD = 1.4 厘米∴ AB＜CD或 CD＞AB叠合法将线段重叠在一起，使一个端点重合，再进行比较.线段的长短比较ABCDAB = 0.8l 厘米CD = 1.4 厘米∴ AB＜CD或 CD＞AB叠合法将线段重叠在一起，使一个端点重合，再进行比较.线段的长短比较AB = 0.8 厘米度量法先分别量出各线段的长度，再比较长短.线段的长短比较ABCDAB = 0.8 厘米CD = 1.4 厘米度量法先分别量出各线段的长度，再比较长短.线段的长短比较ABCDAB = 0.8 厘米CD = 1.4 厘米∴ AB＜CD或 CD＞AB度量法先分别量出各线段的长度，再比较长短. 你能用直尺（没有刻度）和圆规画一条线段等于已知线段吗？
已知线段a，作线段AB，使线段AB＝a． 问题探究三问题探究四：动手操作 在一张透明的纸上画一条线段AB，折叠纸片，使端点A、B重合，折痕与线段的交点我们叫作线段的中点，你能给线段下定义吗？由线段的中点，你能得到哪
些线段之间的数量关系？ 线段中点：把一条线段分成相等两部分的点叫线段的中点． 例1. 在直线a上顺次截取A,B,C三点，使得 AB=4cm,BC=3cm.如果o是线段AC的中点,求线段OB的长。
练习如图，AB = 6厘米，点C是线段AB的中点，点D是线段AB的中点，求线段AD的长.6厘米？厘米∵ 点C是线段AB的中点，∴ AC = BC = AB = 3厘米∵ 点D是线段BC的中点，∴ CD = BC = 1.5厘米∴ AD = AC + CD= 3 + 1.5= 4.5厘米小结
直线、射线、线段的概念和表示；
线段的比较方法：度量法、叠合法；
线段的中点：把一条线段分成相等两部分的点
直线的性质：两点确定一条直线；
5.线段的性质：两点之间线段最短．
6、两点之间的距离：两点之间线段的长度。1、下列图形能比较大小的是（ ）
A、直线与线段
B、直线与射线
C、两条线段
D、射线与线段练习：c2.已知直线L上顺次三个点A、B、C，已知AB=10cm,BC=4cm。
（1）如果D是AC的中点，那么AD= cm.
（2）如果M是AB的中点，那么MD= cm.
（3）如图，AB=AC―( ),AM+MB=AD+( )

BACDM（3）如图 AB=6cm，点C是AB的中点，点D是CB的中点，则AD=____cm（4）如图，下列说法 ，不能判断点C是线段AB的中点的是( )
A、AC=CB B、AB=2AC
C、AC+CB=AB D、CB= AB C4.5（5）如图，AD=AB—____=AC+ _____BDCD(10)已知A、B是数轴上的两点，AB = 3，点B表示-1，则点A表示（ ），AB的中点C表示（ ）拓展创新 已知线段AB=10,点C在直线AB上，且AC=4,若点D是AB的中点，求DC的长． 情况一：点C在A的左侧拓展创新 已知线段AB=10,点C在直线AB上，且AC=4,若点D是AB的中点，求DC的长． 情况二：点C在A的右侧