6.6 平方差公式(1)课件
图片预览



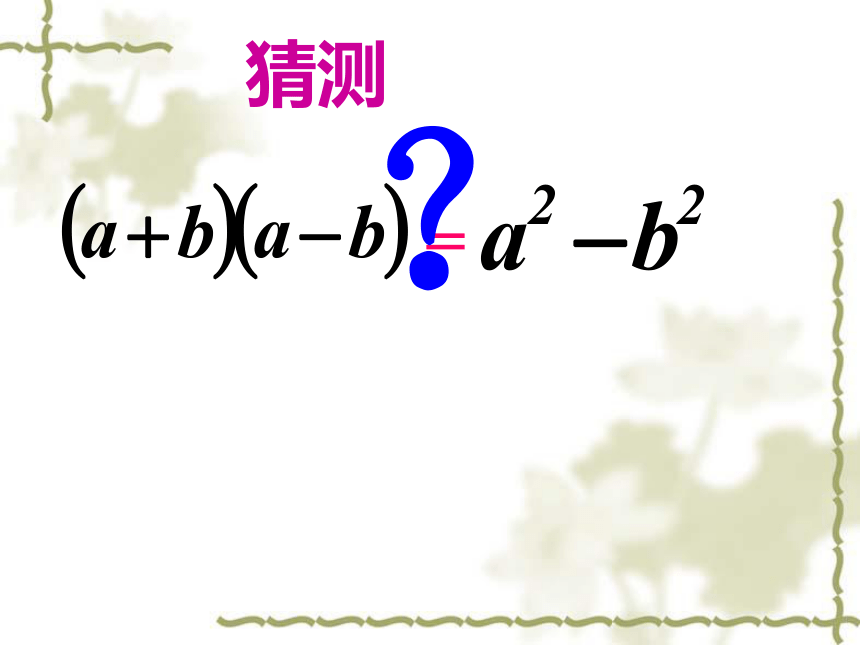


文档简介
课件17张PPT。 平方差公式(1)学习目标探索平方差公式,并牢记平方差公式
熟练应用公式进行简单的计算 按照多项式乘以多项式的法则计算下列题目: (1) (x+2)(x-2)
(2) (1+3a)(1-3a) (3) (x+5y)(x-5y)
(4) (y+3z)(y-3z) 观察以上算式及其计算结果,你发现了什么规律?算式的规律:2)两个二项式中有一项完全相同,另一项互为相反数;3)结果为两个整式差的形式.自学指导1)是两个二项式相乘;结果的规律:4)结果为相同项的平方减互为相反数的项的平方.= ? 猜测 证明:(a+b)(a-b) 我们经历了由发现——猜测——证明的过程,最后得出一个公式性的结论,我们将这个公式叫做平方差公式.即: (a+b)(a-b)两数和与这两数差的积,等于它们的平方差.(多项式乘法法则)(合并同类项)欣赏例1、例2 思考:应用平方差公式时注意些什么?
先确定平方差公式中的“a”和“b”.
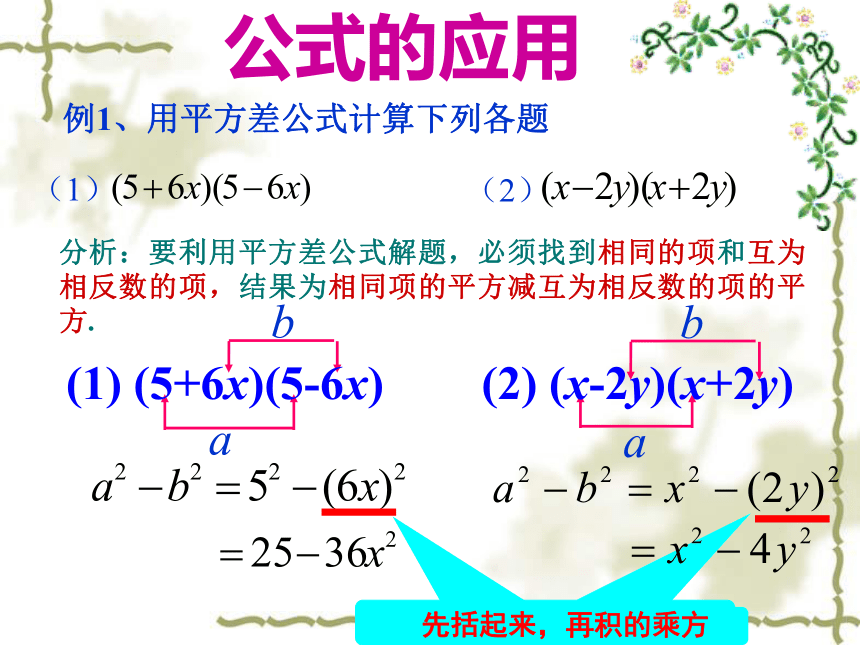
把系数和所有字母一起用括号括起来再平方。公式的应用 例1、用平方差公式计算下列各题(1) (2) (1) (5+6x)(5-6x)(2) (x-2y)(x+2y)分析:要利用平方差公式解题,必须找到相同的项和互为相反数的项,结果为相同项的平方减互为相反数的项的平方.先括起来,再积的乘方(-m+n)(-m-n)(3) (-m+n)(-m-n)解:-m是相同项,要连同符号添加括号。符号相同项,要连同符号添加括号。所有字母添加括号。1)(3m+2n)(3m-2n)
2) (b+2a)(b-2a)
3)
4)(-4a-1)(4a-1)
练 习思考:44页【想一想】 由此你得到什么启示? 判断多项式的结构是否符号平方差公式!45页 随堂练习1训练下列计算对不对?如果不对,怎样改正?
2)错1) 分析:最后结果应是两项的平方差错 3) 分析:应是相同项的平方减互为相反数的项的平方 错 4) 分析:不满足平方差公式的特点,没有相同项 错 分析:应将 当作一个整体,用括号括起来再平方 45页 随堂练习2训练平方差公式重复运用: 计算二次应用一次应用训练计算小 结
1、平方差公式是特殊的多项式乘法,要理解并掌握公式的结构特征.
??? 2、计算中注意公式的重复使用,确保结果最简。 2) 右边是相同项的平方减互为相反数的 项的平方.1) 左边是两个二项式相乘,其中一 项完全相同,另一项互为相反数.
熟练应用公式进行简单的计算 按照多项式乘以多项式的法则计算下列题目: (1) (x+2)(x-2)
(2) (1+3a)(1-3a) (3) (x+5y)(x-5y)
(4) (y+3z)(y-3z) 观察以上算式及其计算结果,你发现了什么规律?算式的规律:2)两个二项式中有一项完全相同,另一项互为相反数;3)结果为两个整式差的形式.自学指导1)是两个二项式相乘;结果的规律:4)结果为相同项的平方减互为相反数的项的平方.= ? 猜测 证明:(a+b)(a-b) 我们经历了由发现——猜测——证明的过程,最后得出一个公式性的结论,我们将这个公式叫做平方差公式.即: (a+b)(a-b)两数和与这两数差的积,等于它们的平方差.(多项式乘法法则)(合并同类项)欣赏例1、例2 思考:应用平方差公式时注意些什么?
先确定平方差公式中的“a”和“b”.
把系数和所有字母一起用括号括起来再平方。公式的应用 例1、用平方差公式计算下列各题(1) (2) (1) (5+6x)(5-6x)(2) (x-2y)(x+2y)分析:要利用平方差公式解题,必须找到相同的项和互为相反数的项,结果为相同项的平方减互为相反数的项的平方.先括起来,再积的乘方(-m+n)(-m-n)(3) (-m+n)(-m-n)解:-m是相同项,要连同符号添加括号。符号相同项,要连同符号添加括号。所有字母添加括号。1)(3m+2n)(3m-2n)
2) (b+2a)(b-2a)
3)
4)(-4a-1)(4a-1)
练 习思考:44页【想一想】 由此你得到什么启示? 判断多项式的结构是否符号平方差公式!45页 随堂练习1训练下列计算对不对?如果不对,怎样改正?
2)错1) 分析:最后结果应是两项的平方差错 3) 分析:应是相同项的平方减互为相反数的项的平方 错 4) 分析:不满足平方差公式的特点,没有相同项 错 分析:应将 当作一个整体,用括号括起来再平方 45页 随堂练习2训练平方差公式重复运用: 计算二次应用一次应用训练计算小 结
1、平方差公式是特殊的多项式乘法,要理解并掌握公式的结构特征.
??? 2、计算中注意公式的重复使用,确保结果最简。 2) 右边是相同项的平方减互为相反数的 项的平方.1) 左边是两个二项式相乘,其中一 项完全相同,另一项互为相反数.
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
