第五单元5.2.2《梯形的认识》(教学设计)-四年级上册数学人教版
文档属性
| 名称 | 第五单元5.2.2《梯形的认识》(教学设计)-四年级上册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-23 14:31:55 | ||
图片预览


文档简介
《梯形的认识》教学设计
备教材内容
1.本节课学习的是教材66页的内容及相关习题。
2.本节课是在学生认识了平行与垂直,认识长方形、正方形和平行四边形的特征、会画平行四边形的高的基础上进行教学的。例3教学认识梯形。教材先提供生活中的实例,然后概括出梯形的定义,再认识梯形各部分的名称,最后给出了等腰梯形、直角梯形的定义和直观图,形成对梯形的完整认识。例4通过回顾已学过的四边形引导学生探讨长方形、正方形和平行四边形之间的关系,进一步从平行的角度认识长方形、正方形边的特征,由此学会用集合图表示四边形之间的关系。
3.本节课学习的梯形在整个小学阶段属于最后一类直线型平面图形,与前面已学的各种图形有着十分密切的联系,本节课的学习也对后续学习梯形面积的计算,解决生活中的设计问题起着至关重要的作用。
备教法学法
学习本节课之前,学生已经掌握了长方形、正方形、平行四边形、三角形等平面图形的本质特征和平行及平行线间的距离等有关内容,为本节课教学做好了一定的知识、技能准备。梯形虽然是学生初次接触的图形,但在实际生活中,学生已建立了一定的表象。只是很难准确地抽象出它的本质属性。在教学中,先用课件呈现丰富的生活原型,帮助学生认识梯形以及感受梯形在生活中的广泛应用。然后学生动手操作,用三角尺推一推、量一量,认识梯形的特征,理解梯形的定义。让学生经历从生活化到数学化的过程,体会数学与生活的密切联系。最后用知识迁移的方法,引领学生探究画梯形的高。在教学直角梯形和等腰梯形的认识时,也是通过动手操作,发现它们各自的特点,理解各自的定义。关于本节课的教学难点——正确用集合图表示长方形、正方形、梯形、平行四边形的关系,采用小组合作的学习方式,通过观察、讨论,得出结论。教学中注重让学生通过观察、操作、推理等手段,发展学生的空间观念,使学生从感性认识逐步上升到理性认识的高度。
备教学目标
1.通过观察、比较、操作等实践活动,认识梯形特征,并概括出梯形的定义。能够画出
梯形的高,认识直角梯形和等腰梯形,并通过分类活动进一步认识四边形。
2. 经历“剪一剪”、“画一画”的过程,通过辨析巩固梯形的概念,发展空间观念。
3. 经历操作、辨析等活动中,积累数学活动经验。
备教学重难点
重点:掌握梯形的特征。
难点:掌握梯形的高的画法。
备已学知识
1.长方形、正方形和平行四边形的特征。
长方形:两组对边分别相等,四个角都是直角。
正方形:四条边都相等,四个角都是直角。
平行四边形:两组对边分别平行,两组对边分别相等。
2.画平行四边形的高。
用画垂线的方法,画平行线间的垂直线段,标注垂足、底、高。
备知识讲解
知识点一 认识梯形
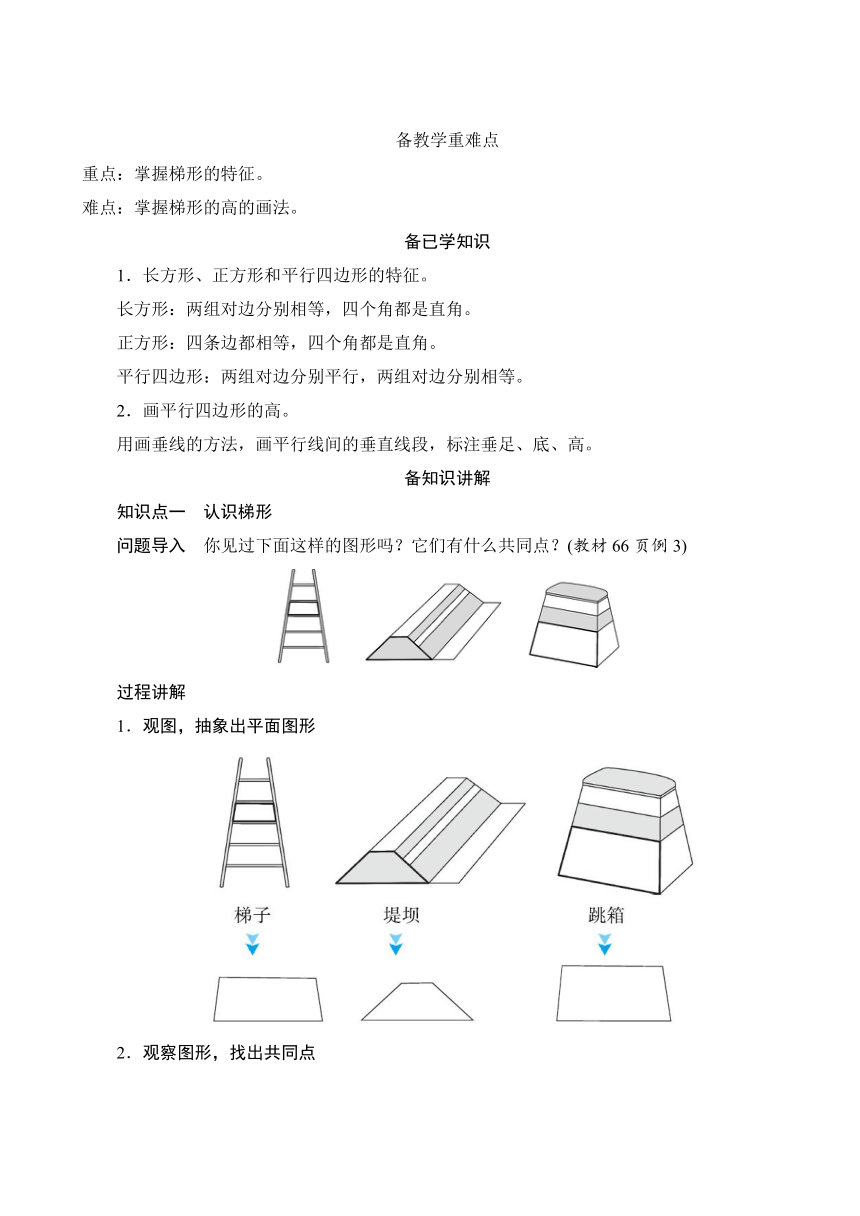
问题导入 你见过下面这样的图形吗?它们有什么共同点?(教材66页例3)
过程讲解
1.观图,抽象出平面图形
2.观察图形,找出共同点
重点提示 判断梯形的两个条件:必须是四边形;只有一组对边平行。
每个图形都有四条边,其中只有一组对边平行,而且互相平行的一组对边的长度不相等。
3.明确梯形的定义
只有一组对边平行的四边形叫做梯形。
4.梯形各部分的名称
在梯形中,互相平行的一组对边叫做梯形的底,通常把较短的底叫做上底,较长的底叫做下底;通过底上的一个点向对边画垂线,这点和垂足之间的线段叫做梯形的高,一个梯形有无数条高;梯形中不平行的一组对边叫做梯形的腰。如上图。
5.梯形高的画法
(1)画高的方法:相当于过直线外一点画已知直线的垂线,即在梯形的底上选一点向对边画一条垂线,这点和垂足之间的线段就是梯形的高。从梯形的两个底上任取一点,都可以向它的对边画高,但通常从上底的一个顶点向它的对边画高。
(2)画高的注意事项。
①所画的高用虚线表示。②一定要标直角符号。③一般把高画在图形 内,而不把高画在底边的延长线上。如右图。
6.特殊的梯形
重点提示
等腰梯形的两腰相等,两个底角也相等;直角梯形的一条高就是垂直于上底、下底的腰。
(1)等腰梯形:两腰相等的梯形叫做等腰梯形(如图1)。
(2)直角梯形:有一个角是直角的梯形叫做直角梯形(如图2)。
归纳总结
1.梯形的定义:只有一组对边平行的四边形叫做梯形。
2.梯形各部分的名称。
3.两腰相等的梯形叫做等腰梯形;有一个角是直角的梯形叫做直角梯形。
知识点二 四边形之间的关系
问题导入 我们认识了哪些四边形?(教材66页例4)
过程讲解
1.列举学过的四边形
2.比较各种四边形的特征
四边形 边数 对边是 否平行 对角是 否相等 对边是 否相等
正方形 4 是 是,且四个角都是直角 是,且四条边都相等
长方形 4 是 是,且四个角都是直角 是
平行四边形 4 是 是 是
梯形 4 只有一组 对边平行 否 平行的一组对边不相等;等腰梯形的两腰相等
3.探究长方形、正方形和平行四边形之间的关系
通过观察表格中各种四边形的特征发现:
(1)长方形和正方形具有平行四边形的所有特征,所以长方形和正方形是特殊的平行四边形。
(2)正方形具有长方形的所有特征,所以正方形是特殊的长方形。
4.将正方形、长方形、平行四边形和梯形分类
根据对边平行的情况可以把长方形、正方形、平行四边形和梯形分成两类:
(1)两组对边分别平行:长方形、正方形和平行四边形。
(2)只有一组对边平行:梯形。
5.用集合图表示四边形之间的关系
[思想方法解读:用集合图表示各种四边形之间的关系,渗透了集合思想。集合思想就是运用集合的概念、逻辑语言、运算、图形等来解决数学问题的思想方法。]
归纳总结
1.正方形是特殊的长方形。
2.长方形和正方形是特殊的平行四边形。
备易错易混
误区 判断:有一组对边平行的四边形是梯形。(√)
错解分析 此题错在没有准确掌握梯形的特征。“有一组对边平行”和“只有一组对边平行”有着本质的区别。“有一组对边平行”并不能说明另一组对边不平行,而“只有一组对边平行”除了说明本身这一组对边平行外,还强调另一组对边不平行。
错解改正 ×
温馨提示
梯形只有一组对边平行。
备综合能力
思维开放 运用分类法和数线段的方法解决数图形的问题
典型例题 数一数下面的图形中有几个平行四边形和梯形。
思路分析 思路一 要不重复、不遗漏地数出每种图形的个数,可以分类来数。先数单个图形的个数,再数组合图形的个数。平行四边形要在两组平行线之间找。列表如下:
数的 方式 单个小平行 四边形 由2个平行四 边形组合 由3个平行四 边形组合
图形
个数 3 2 1
梯形要分左、右两组来数。数的方法与数平行四边形的方法相同,先分别数出左、右两组中梯形的个数,再相加。
思路二 一条线段上有n条基本线段,则这条线段上一共有[n+(n-1)+(n-2)+…+1]条线段。
图中大平行四边形的左边上有3条基本线段,一共有3+2+1=6(条)线段,分别以这6条线段中的一条为一条边的平行四边形共有6个。
图中分别以大平行四边形左边的6条线段中的一条为一条腰的梯形共有6个,分别以大平行四边形右边的6条线段中的一条为一条腰的梯形也共有6个,一共有6×2=12(个)梯形。
正确解答 有6个平行四边形和12个梯形。
方法总结 数图形的个数时,要按照一定的顺序数,做到不重复、不遗漏。
方法运用 运用转化法解决求周长的问题
典型例题 右图是一条方形螺线。已知每相邻两条平行线之间的距离为1厘米,求螺线的总长度。(图中单位:厘米)
思路分析 可先将图形切割、拼组转化,再求螺线的总长度。如图所示,按箭头方向转动虚线部分,能够将图形转化成三个边长分别为3厘米、5厘米、7厘米的正方形和中间的一个边长为1厘米的 。(图中单位:厘米)
正确解答 (3+5+7)×4+1×3=63(厘米)
答:螺线的总长度是63厘米。
方法提示 解决此题时,先用切割、拼组等方法将已知图形转化成规则图形,再求总长度。
备教学资源
梯形金字塔
古代埃及玛斯塔巴形式的王室坟墓一直沿用到第三王朝,左塞王梯形金字塔(或称层级金字塔)是坟墓建筑史上重要的里程碑。
左塞王梯形金字塔是高61.2米,底边东西长143米、南北长125米的六级阶梯形金字塔,梯形金字塔虽然很快被更高更大的建筑物所超越,但是直到拉美西斯二世时代,它仍然是令人敬畏的。
为什么堤坝的横截面要修成梯形
1.防水压。
随着水的深度的增加,压强也随之增加,水越深,压强越大,所以把堤坝修成下宽上窄的形状可以使堤坝承受较大的水压。
2.防渗漏。
堤坝下部受水的压强越大,水越容易渗进坝体。把下部修得宽些,就可以延长堤坝内水的渗透路径,增大渗透阻力,从而提高堤坝的防渗透性能。
3.防滑动。
堤坝内水的压力总有将堤坝向外水平推动和将堤坝推向下游的运动趋势,堤坝基底需要有与之抗衡的静摩擦力,才能保持堤坝平衡。将堤坝下部修宽,既可以增大坝体的重力,又可以增大迎水面上水对坝体竖直向下的压力,因此,可以增强坝体与坝基间的最大静摩擦力,以达到防止堤坝滑动的目的。
备教材内容
1.本节课学习的是教材66页的内容及相关习题。
2.本节课是在学生认识了平行与垂直,认识长方形、正方形和平行四边形的特征、会画平行四边形的高的基础上进行教学的。例3教学认识梯形。教材先提供生活中的实例,然后概括出梯形的定义,再认识梯形各部分的名称,最后给出了等腰梯形、直角梯形的定义和直观图,形成对梯形的完整认识。例4通过回顾已学过的四边形引导学生探讨长方形、正方形和平行四边形之间的关系,进一步从平行的角度认识长方形、正方形边的特征,由此学会用集合图表示四边形之间的关系。
3.本节课学习的梯形在整个小学阶段属于最后一类直线型平面图形,与前面已学的各种图形有着十分密切的联系,本节课的学习也对后续学习梯形面积的计算,解决生活中的设计问题起着至关重要的作用。
备教法学法
学习本节课之前,学生已经掌握了长方形、正方形、平行四边形、三角形等平面图形的本质特征和平行及平行线间的距离等有关内容,为本节课教学做好了一定的知识、技能准备。梯形虽然是学生初次接触的图形,但在实际生活中,学生已建立了一定的表象。只是很难准确地抽象出它的本质属性。在教学中,先用课件呈现丰富的生活原型,帮助学生认识梯形以及感受梯形在生活中的广泛应用。然后学生动手操作,用三角尺推一推、量一量,认识梯形的特征,理解梯形的定义。让学生经历从生活化到数学化的过程,体会数学与生活的密切联系。最后用知识迁移的方法,引领学生探究画梯形的高。在教学直角梯形和等腰梯形的认识时,也是通过动手操作,发现它们各自的特点,理解各自的定义。关于本节课的教学难点——正确用集合图表示长方形、正方形、梯形、平行四边形的关系,采用小组合作的学习方式,通过观察、讨论,得出结论。教学中注重让学生通过观察、操作、推理等手段,发展学生的空间观念,使学生从感性认识逐步上升到理性认识的高度。
备教学目标
1.通过观察、比较、操作等实践活动,认识梯形特征,并概括出梯形的定义。能够画出
梯形的高,认识直角梯形和等腰梯形,并通过分类活动进一步认识四边形。
2. 经历“剪一剪”、“画一画”的过程,通过辨析巩固梯形的概念,发展空间观念。
3. 经历操作、辨析等活动中,积累数学活动经验。
备教学重难点
重点:掌握梯形的特征。
难点:掌握梯形的高的画法。
备已学知识
1.长方形、正方形和平行四边形的特征。
长方形:两组对边分别相等,四个角都是直角。
正方形:四条边都相等,四个角都是直角。
平行四边形:两组对边分别平行,两组对边分别相等。
2.画平行四边形的高。
用画垂线的方法,画平行线间的垂直线段,标注垂足、底、高。
备知识讲解
知识点一 认识梯形
问题导入 你见过下面这样的图形吗?它们有什么共同点?(教材66页例3)
过程讲解
1.观图,抽象出平面图形
2.观察图形,找出共同点
重点提示 判断梯形的两个条件:必须是四边形;只有一组对边平行。
每个图形都有四条边,其中只有一组对边平行,而且互相平行的一组对边的长度不相等。
3.明确梯形的定义
只有一组对边平行的四边形叫做梯形。
4.梯形各部分的名称
在梯形中,互相平行的一组对边叫做梯形的底,通常把较短的底叫做上底,较长的底叫做下底;通过底上的一个点向对边画垂线,这点和垂足之间的线段叫做梯形的高,一个梯形有无数条高;梯形中不平行的一组对边叫做梯形的腰。如上图。
5.梯形高的画法
(1)画高的方法:相当于过直线外一点画已知直线的垂线,即在梯形的底上选一点向对边画一条垂线,这点和垂足之间的线段就是梯形的高。从梯形的两个底上任取一点,都可以向它的对边画高,但通常从上底的一个顶点向它的对边画高。
(2)画高的注意事项。
①所画的高用虚线表示。②一定要标直角符号。③一般把高画在图形 内,而不把高画在底边的延长线上。如右图。
6.特殊的梯形
重点提示
等腰梯形的两腰相等,两个底角也相等;直角梯形的一条高就是垂直于上底、下底的腰。
(1)等腰梯形:两腰相等的梯形叫做等腰梯形(如图1)。
(2)直角梯形:有一个角是直角的梯形叫做直角梯形(如图2)。
归纳总结
1.梯形的定义:只有一组对边平行的四边形叫做梯形。
2.梯形各部分的名称。
3.两腰相等的梯形叫做等腰梯形;有一个角是直角的梯形叫做直角梯形。
知识点二 四边形之间的关系
问题导入 我们认识了哪些四边形?(教材66页例4)
过程讲解
1.列举学过的四边形
2.比较各种四边形的特征
四边形 边数 对边是 否平行 对角是 否相等 对边是 否相等
正方形 4 是 是,且四个角都是直角 是,且四条边都相等
长方形 4 是 是,且四个角都是直角 是
平行四边形 4 是 是 是
梯形 4 只有一组 对边平行 否 平行的一组对边不相等;等腰梯形的两腰相等
3.探究长方形、正方形和平行四边形之间的关系
通过观察表格中各种四边形的特征发现:
(1)长方形和正方形具有平行四边形的所有特征,所以长方形和正方形是特殊的平行四边形。
(2)正方形具有长方形的所有特征,所以正方形是特殊的长方形。
4.将正方形、长方形、平行四边形和梯形分类
根据对边平行的情况可以把长方形、正方形、平行四边形和梯形分成两类:
(1)两组对边分别平行:长方形、正方形和平行四边形。
(2)只有一组对边平行:梯形。
5.用集合图表示四边形之间的关系
[思想方法解读:用集合图表示各种四边形之间的关系,渗透了集合思想。集合思想就是运用集合的概念、逻辑语言、运算、图形等来解决数学问题的思想方法。]
归纳总结
1.正方形是特殊的长方形。
2.长方形和正方形是特殊的平行四边形。
备易错易混
误区 判断:有一组对边平行的四边形是梯形。(√)
错解分析 此题错在没有准确掌握梯形的特征。“有一组对边平行”和“只有一组对边平行”有着本质的区别。“有一组对边平行”并不能说明另一组对边不平行,而“只有一组对边平行”除了说明本身这一组对边平行外,还强调另一组对边不平行。
错解改正 ×
温馨提示
梯形只有一组对边平行。
备综合能力
思维开放 运用分类法和数线段的方法解决数图形的问题
典型例题 数一数下面的图形中有几个平行四边形和梯形。
思路分析 思路一 要不重复、不遗漏地数出每种图形的个数,可以分类来数。先数单个图形的个数,再数组合图形的个数。平行四边形要在两组平行线之间找。列表如下:
数的 方式 单个小平行 四边形 由2个平行四 边形组合 由3个平行四 边形组合
图形
个数 3 2 1
梯形要分左、右两组来数。数的方法与数平行四边形的方法相同,先分别数出左、右两组中梯形的个数,再相加。
思路二 一条线段上有n条基本线段,则这条线段上一共有[n+(n-1)+(n-2)+…+1]条线段。
图中大平行四边形的左边上有3条基本线段,一共有3+2+1=6(条)线段,分别以这6条线段中的一条为一条边的平行四边形共有6个。
图中分别以大平行四边形左边的6条线段中的一条为一条腰的梯形共有6个,分别以大平行四边形右边的6条线段中的一条为一条腰的梯形也共有6个,一共有6×2=12(个)梯形。
正确解答 有6个平行四边形和12个梯形。
方法总结 数图形的个数时,要按照一定的顺序数,做到不重复、不遗漏。
方法运用 运用转化法解决求周长的问题
典型例题 右图是一条方形螺线。已知每相邻两条平行线之间的距离为1厘米,求螺线的总长度。(图中单位:厘米)
思路分析 可先将图形切割、拼组转化,再求螺线的总长度。如图所示,按箭头方向转动虚线部分,能够将图形转化成三个边长分别为3厘米、5厘米、7厘米的正方形和中间的一个边长为1厘米的 。(图中单位:厘米)
正确解答 (3+5+7)×4+1×3=63(厘米)
答:螺线的总长度是63厘米。
方法提示 解决此题时,先用切割、拼组等方法将已知图形转化成规则图形,再求总长度。
备教学资源
梯形金字塔
古代埃及玛斯塔巴形式的王室坟墓一直沿用到第三王朝,左塞王梯形金字塔(或称层级金字塔)是坟墓建筑史上重要的里程碑。
左塞王梯形金字塔是高61.2米,底边东西长143米、南北长125米的六级阶梯形金字塔,梯形金字塔虽然很快被更高更大的建筑物所超越,但是直到拉美西斯二世时代,它仍然是令人敬畏的。
为什么堤坝的横截面要修成梯形
1.防水压。
随着水的深度的增加,压强也随之增加,水越深,压强越大,所以把堤坝修成下宽上窄的形状可以使堤坝承受较大的水压。
2.防渗漏。
堤坝下部受水的压强越大,水越容易渗进坝体。把下部修得宽些,就可以延长堤坝内水的渗透路径,增大渗透阻力,从而提高堤坝的防渗透性能。
3.防滑动。
堤坝内水的压力总有将堤坝向外水平推动和将堤坝推向下游的运动趋势,堤坝基底需要有与之抗衡的静摩擦力,才能保持堤坝平衡。将堤坝下部修宽,既可以增大坝体的重力,又可以增大迎水面上水对坝体竖直向下的压力,因此,可以增强坝体与坝基间的最大静摩擦力,以达到防止堤坝滑动的目的。
