29.5正多边形与圆随堂练习(含答案)冀教版数学九年级下册
文档属性
| 名称 | 29.5正多边形与圆随堂练习(含答案)冀教版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 633.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-23 00:00:00 | ||
图片预览



文档简介
29.5正多边形与圆随堂练习-冀教版数学九年级下册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知圆周角∠ACB=130°,则圆心角∠AOB=( )
A.130° B.115° C.100° D.50°
2.正方形的外接圆半径与内切圆的半径之比为( )
A.:1 B.2:1 C.1: D.1:2
3.⊙O的半径OA=6 cm,扇形AOB的圆心角是120°,则扇形面积是( )
A.6π cm2 B.8π cm2 C.12π cm2 D.24π cm2
4.△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是( )
A.80° B.160° C.80°或20° D.80°或100°
5.阅读理解:如图 所示,在平面内选一定点 ,引一条有方向的射线 ,再选定一个单位长度,那么平面上任一点 的位置可由 的长度 与 的度数 确定,有序数对 称为 点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图 的极坐标系下,如果正六边形的边长为 ,有一边 在射线 上,则正六边形的顶点 的极坐标应记为( )
A. B. C. D.
6.如图所示,小明从半径为的圆形纸片中剪下圆周的一个扇形,然后利用剪下的扇形制作成一个圆锥形玩具纸帽(接缝处不重叠),那么这个圆锥的高为( )
A. B. C. D.
7.将边长为2的正五边形沿对角线折叠,使点A落在正五边形内部的点M处,则下列说法正确的是( )
A.点E、M、C在同一条直线上 B.点M是这个五边形外接圆圆心
C. D.点M到直线、的距离相等
8.一个正三角形和一个正六边形的面积相等,则它们的边长比为( )
A.﹕1 B.﹕1 C.﹕1 D.﹕1
9.下列关于正多边形的叙述,正确的是( )
A.正七边形既是轴对称图形又是中心对称图形
B.存在一个正多边形,它的外角和为
C.任何正多边形都有一个外接圆
D.不存在每个外角都是对应每个内角两倍的正多边形
10.如图,△ABC是圆O的内接正三角形,弦EF过BC的中点D,且EF∥AB,若AB=4,则DE的长为( )
A.1 B.﹣1 C. D.2
二、填空题
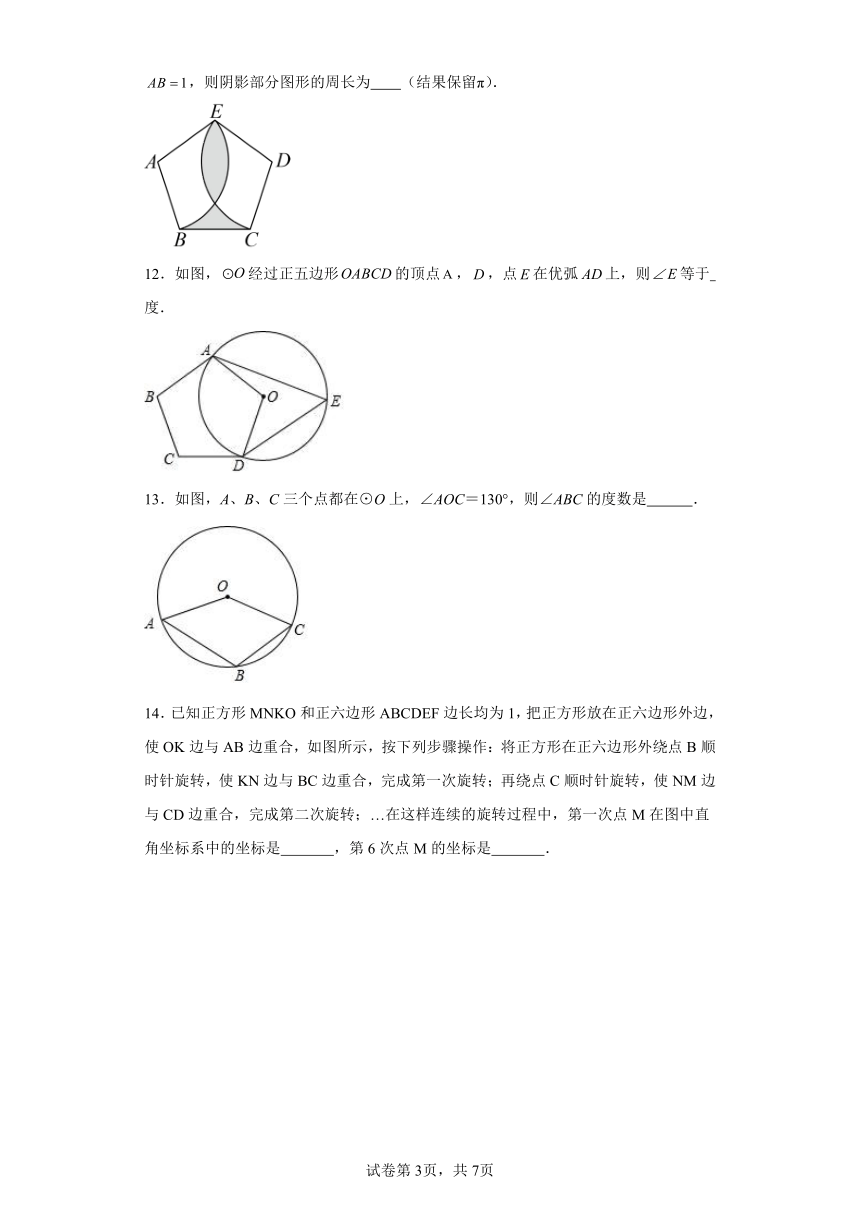
11.如图,分别以正五边形的顶点A,D为圆心,以长为半径画,.若,则阴影部分图形的周长为 (结果保留π).
12.如图,经过正五边形的顶点,,点在优弧上,则等于 度.
13.如图,A、B、C三个点都在⊙O上,∠AOC=130°,则∠ABC的度数是 .
14.已知正方形MNKO和正六边形ABCDEF边长均为1,把正方形放在正六边形外边,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形外绕点B顺时针旋转,使KN边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使NM边与CD边重合,完成第二次旋转;…在这样连续的旋转过程中,第一次点M在图中直角坐标系中的坐标是 ,第6次点M的坐标是 .
15.古人认为“天圆地方”,故以圆璧祭天,以玉琮祭地,《周礼·春官·大宗伯》记载“以玉作六器,以礼天地四方”,长江流域良渚文化,创制美玉,尤以琮(如图1所示)、璧最为经典. 琮为内圆外方之器,此玉琮素面琢磨细腻,色泽温润,两端射口稍露,比例恰到好处. 如图2,是“琮”的横截面的示意图,其“外方”是一个边长为的正方形,内圆圆O的圆心与正方形的中心重合,正方形的四个角上各有一个腰长为的等腰,圆O与其斜边相切,则圆O的半径为 .
16.如图,已知正六边形ABCDEF的边长是5,点P是AD上的一动点,则PE+PF的最小值是 .
17.如图,六个含30°角的直角三角板拼出两个正六边形,若大正六边形的面积为6,则中间小正六边形的面积为 .
18.如图,边长为的正六边形ABCDEF的顶点A、B在圆O上,顶点C、D、E、F在该圆内,∠AOB=36°,将正六边形ABCDEF绕点A逆时针旋转,当点F第一次落在圆上时,点E运动的路线长是 (结果保留π).
19.我国魏晋时期著名的数学家刘徽在《九章算术》中提出了“割圆术——割之弥细,所失弥少,隔之又割,以至不可割,则与圆周合体,而无所失也.”也就是利用圆的内接多边形逐步逼近圆的方法来近似计算圆的面积和周长.如图1,若用圆的内接正六边形的面积来近似估计半径为1的⊙O的面积,再用如图2的圆的内接正十二边形的面积来近似估计半径为1的⊙O的面积,则 .(结果保留根号)
20.如图,点、、在上,若,则 .
三、解答题
21.如图,四边形内接于,,,垂足为.
(1)若,求的度数;
(2)求证:.
22.如图,在正方形中,是边上的动点(与点、不重合),且,于点,与的延长线交于点,连接、.
(1)求证:①;②;
(2)若,在点运动过程中,探究:
①线段的长度是否改变?若不变,求出这个定值;若改变,请说明理由;
②当为何值时,为等腰直角三角形.
23.已知⊙O的直径AB=4,点C在⊙O上,连接AC,沿AC折叠劣弧,记折叠后的劣弧为.
(1)如图1,当经过圆心O时,求的长.
(2)如图2,当与AB相切于A时.
①画出所在的圆的圆心P.
②求出阴影部分弓形的面积.
24.(1)如图①,M、N分别是⊙O的内接正△ABC的边AB、BC上的点,且BM=CN,连接OM,ON,求∠MON的度数.
(2)图②、③、…… ④中,M、N分别是⊙O的内接正方形ABCD、正五边ABCDE、……正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON;则图②中∠MON的度数是__________,图③中∠MON的度数是__________;……由此可猜测在n边形图中∠MON的度数是_______
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.A
3.C
4.D
5.A
6.C
7.A
8.A
9.C
10.B
11.
12.54
13.115°.
14.
15.
16.10
17.
18.
19.
20.
21.(1);(2)略
22.(1)略;(2)①在点运动过程中,的长度不变,且CG=2;②AE=.
23.(1)的长=;(2)①P点为所求,见解析; ②S阴=π-2.
24.(1)120°
(2)90°、72°、°
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知圆周角∠ACB=130°,则圆心角∠AOB=( )
A.130° B.115° C.100° D.50°
2.正方形的外接圆半径与内切圆的半径之比为( )
A.:1 B.2:1 C.1: D.1:2
3.⊙O的半径OA=6 cm,扇形AOB的圆心角是120°,则扇形面积是( )
A.6π cm2 B.8π cm2 C.12π cm2 D.24π cm2
4.△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是( )
A.80° B.160° C.80°或20° D.80°或100°
5.阅读理解:如图 所示,在平面内选一定点 ,引一条有方向的射线 ,再选定一个单位长度,那么平面上任一点 的位置可由 的长度 与 的度数 确定,有序数对 称为 点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图 的极坐标系下,如果正六边形的边长为 ,有一边 在射线 上,则正六边形的顶点 的极坐标应记为( )
A. B. C. D.
6.如图所示,小明从半径为的圆形纸片中剪下圆周的一个扇形,然后利用剪下的扇形制作成一个圆锥形玩具纸帽(接缝处不重叠),那么这个圆锥的高为( )
A. B. C. D.
7.将边长为2的正五边形沿对角线折叠,使点A落在正五边形内部的点M处,则下列说法正确的是( )
A.点E、M、C在同一条直线上 B.点M是这个五边形外接圆圆心
C. D.点M到直线、的距离相等
8.一个正三角形和一个正六边形的面积相等,则它们的边长比为( )
A.﹕1 B.﹕1 C.﹕1 D.﹕1
9.下列关于正多边形的叙述,正确的是( )
A.正七边形既是轴对称图形又是中心对称图形
B.存在一个正多边形,它的外角和为
C.任何正多边形都有一个外接圆
D.不存在每个外角都是对应每个内角两倍的正多边形
10.如图,△ABC是圆O的内接正三角形,弦EF过BC的中点D,且EF∥AB,若AB=4,则DE的长为( )
A.1 B.﹣1 C. D.2
二、填空题
11.如图,分别以正五边形的顶点A,D为圆心,以长为半径画,.若,则阴影部分图形的周长为 (结果保留π).
12.如图,经过正五边形的顶点,,点在优弧上,则等于 度.
13.如图,A、B、C三个点都在⊙O上,∠AOC=130°,则∠ABC的度数是 .
14.已知正方形MNKO和正六边形ABCDEF边长均为1,把正方形放在正六边形外边,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形外绕点B顺时针旋转,使KN边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使NM边与CD边重合,完成第二次旋转;…在这样连续的旋转过程中,第一次点M在图中直角坐标系中的坐标是 ,第6次点M的坐标是 .
15.古人认为“天圆地方”,故以圆璧祭天,以玉琮祭地,《周礼·春官·大宗伯》记载“以玉作六器,以礼天地四方”,长江流域良渚文化,创制美玉,尤以琮(如图1所示)、璧最为经典. 琮为内圆外方之器,此玉琮素面琢磨细腻,色泽温润,两端射口稍露,比例恰到好处. 如图2,是“琮”的横截面的示意图,其“外方”是一个边长为的正方形,内圆圆O的圆心与正方形的中心重合,正方形的四个角上各有一个腰长为的等腰,圆O与其斜边相切,则圆O的半径为 .
16.如图,已知正六边形ABCDEF的边长是5,点P是AD上的一动点,则PE+PF的最小值是 .
17.如图,六个含30°角的直角三角板拼出两个正六边形,若大正六边形的面积为6,则中间小正六边形的面积为 .
18.如图,边长为的正六边形ABCDEF的顶点A、B在圆O上,顶点C、D、E、F在该圆内,∠AOB=36°,将正六边形ABCDEF绕点A逆时针旋转,当点F第一次落在圆上时,点E运动的路线长是 (结果保留π).
19.我国魏晋时期著名的数学家刘徽在《九章算术》中提出了“割圆术——割之弥细,所失弥少,隔之又割,以至不可割,则与圆周合体,而无所失也.”也就是利用圆的内接多边形逐步逼近圆的方法来近似计算圆的面积和周长.如图1,若用圆的内接正六边形的面积来近似估计半径为1的⊙O的面积,再用如图2的圆的内接正十二边形的面积来近似估计半径为1的⊙O的面积,则 .(结果保留根号)
20.如图,点、、在上,若,则 .
三、解答题
21.如图,四边形内接于,,,垂足为.
(1)若,求的度数;
(2)求证:.
22.如图,在正方形中,是边上的动点(与点、不重合),且,于点,与的延长线交于点,连接、.
(1)求证:①;②;
(2)若,在点运动过程中,探究:
①线段的长度是否改变?若不变,求出这个定值;若改变,请说明理由;
②当为何值时,为等腰直角三角形.
23.已知⊙O的直径AB=4,点C在⊙O上,连接AC,沿AC折叠劣弧,记折叠后的劣弧为.
(1)如图1,当经过圆心O时,求的长.
(2)如图2,当与AB相切于A时.
①画出所在的圆的圆心P.
②求出阴影部分弓形的面积.
24.(1)如图①,M、N分别是⊙O的内接正△ABC的边AB、BC上的点,且BM=CN,连接OM,ON,求∠MON的度数.
(2)图②、③、…… ④中,M、N分别是⊙O的内接正方形ABCD、正五边ABCDE、……正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON;则图②中∠MON的度数是__________,图③中∠MON的度数是__________;……由此可猜测在n边形图中∠MON的度数是_______
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.A
3.C
4.D
5.A
6.C
7.A
8.A
9.C
10.B
11.
12.54
13.115°.
14.
15.
16.10
17.
18.
19.
20.
21.(1);(2)略
22.(1)略;(2)①在点运动过程中,的长度不变,且CG=2;②AE=.
23.(1)的长=;(2)①P点为所求,见解析; ②S阴=π-2.
24.(1)120°
(2)90°、72°、°
答案第1页,共2页
答案第1页,共2页
