冀教版数学九年级下册 29.4切线长定理随堂练习(无答案)
文档属性
| 名称 | 冀教版数学九年级下册 29.4切线长定理随堂练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 440.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-23 18:28:31 | ||
图片预览

文档简介
29.4切线长定理随堂练习-冀教版数学九年级下册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列命题中错误的有( )
①平分弦的直径垂直于弦,并且平分弦所对的两条弧;
②在同圆或等圆中,相等的圆心角所对的弧相等;
③三个点确定一个圆
④反比例函数的图像在一、三象限,y随x的增大而减小
⑤三角形的内心到各边的距离相等,三角形的外心是三条边垂直平分线的交点
A.1个 B.2个 C.3个 D.4个
2.如图,的顶点是上的一个动点,,,边,分别交于点,,分别过点,作的切线交于点,且点恰好在边上,连接,若的半径为,则的最大值为( )
A. B. C. D.
3.如图,点是的内心,,,,于点,则的长为( )
A.2 B.4 C.5 D.6.
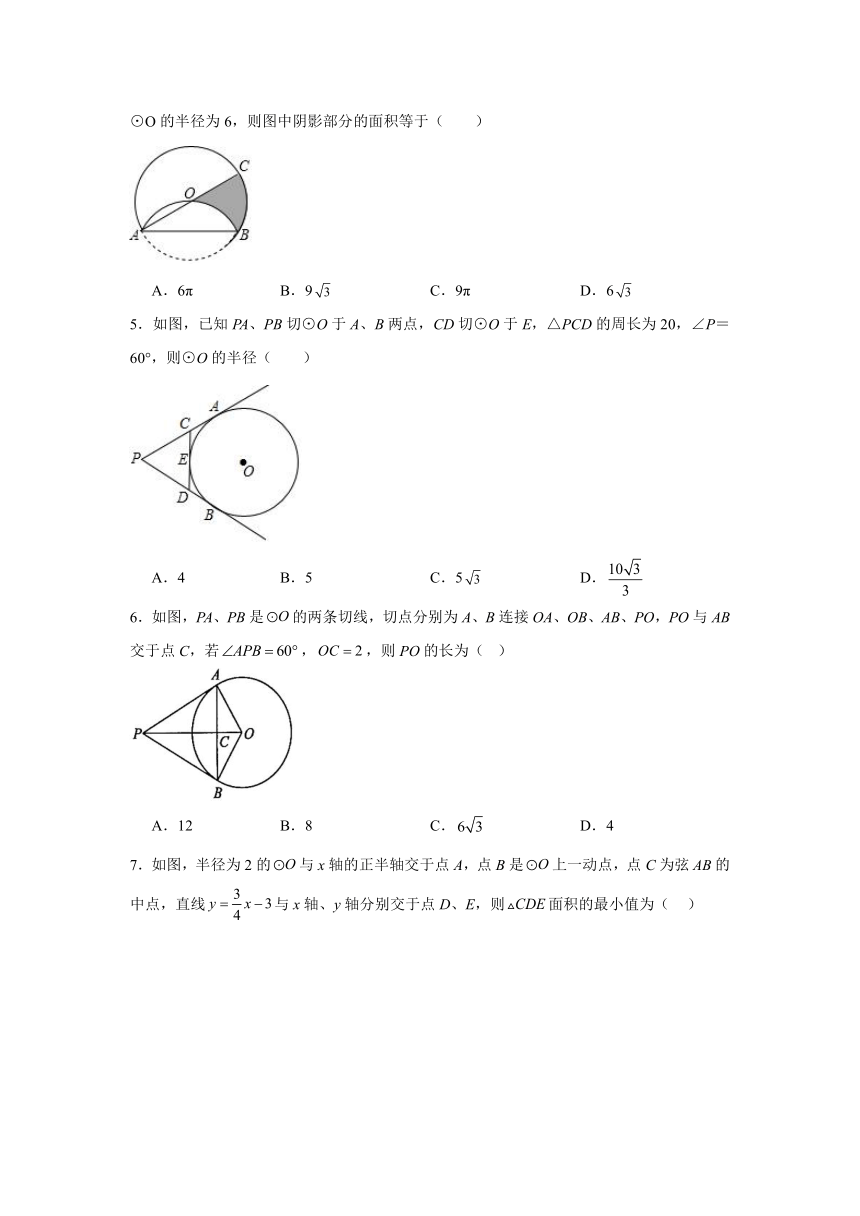
4.如图,AB是⊙O的弦,AC是⊙O的直径,将沿着AB弦翻折,恰好经过圆心O.若⊙O的半径为6,则图中阴影部分的面积等于( )
A.6π B.9 C.9π D.6
5.如图,已知PA、PB切⊙O于A、B两点,CD切⊙O于E,△PCD的周长为20,∠P=60°,则⊙O的半径( )
A.4 B.5 C.5 D.
6.如图,PA、PB是的两条切线,切点分别为A、B连接OA、OB、AB、PO,PO与AB交于点C,若,,则PO的长为( )
A.12 B.8 C. D.4
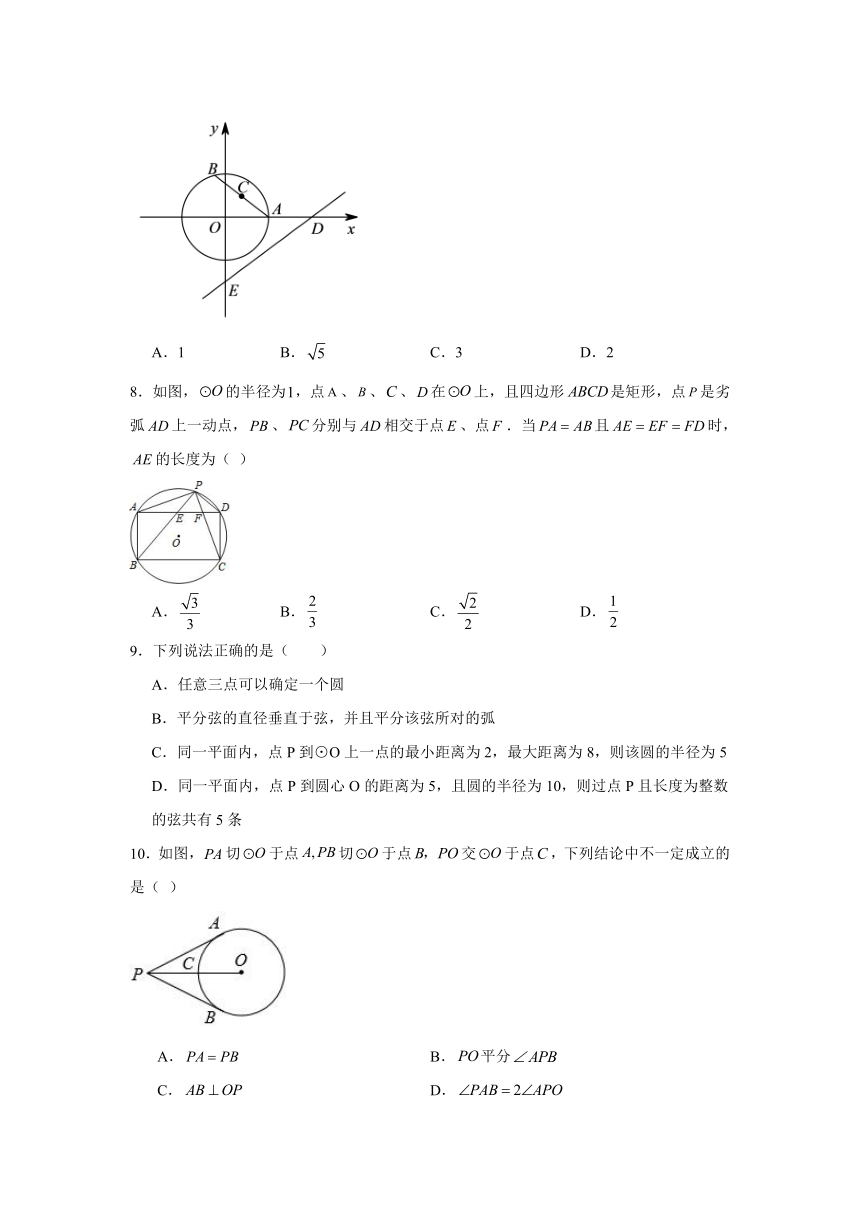
7.如图,半径为2的与x轴的正半轴交于点A,点B是上一动点,点C为弦的中点,直线与x轴、y轴分别交于点D、E,则面积的最小值为( )
A.1 B. C.3 D.2
8.如图,的半径为,点、、、在上,且四边形是矩形,点是劣弧上一动点,、分别与相交于点、点.当且时,的长度为( )
A. B. C. D.
9.下列说法正确的是( )
A.任意三点可以确定一个圆
B.平分弦的直径垂直于弦,并且平分该弦所对的弧
C.同一平面内,点P到⊙O上一点的最小距离为2,最大距离为8,则该圆的半径为5
D.同一平面内,点P到圆心O的距离为5,且圆的半径为10,则过点P且长度为整数的弦共有5条
10.如图,切于点切于点交于点,下列结论中不一定成立的是( )
A. B.平分
C. D.
二、填空题
11.如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交于点E,以点O为圆心,OC的长为半径作交OB于点D,若OA=2,则阴影部分的面积为 .
12.如图,为的直径,点在的延长线上,,与相切,切点分别为,.若,,则
13.三边长分别是5cm,12cm,13cm的三角形的内切圆半径为 cm.
14.如图,已知为的直径,、为的切线,、为切点,交于点,的延长线交于点,连接、.给出以下结论:①;②;③点为的内心.其中正确的是 (填序号).
15.如图,∠ACB=60°,半径为3cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是 cm.
16.如图,在直角坐标系中,已知点A(6,0),B(6,),C(0,),点P为平面内一点,连接BP,OP,CP,且,则CP的最小值为 .
17.如图,在平面直角坐标系中,⊙P的半径为5,圆心P坐标是(5,a)(a>5),函数y=x的图象被⊙P截得的弦AB的长为4,则a的值是 .
18.已知O,I分别是△ABC的外心和内心,∠BOC=140°,则∠BIC的大小是 .
19.如图,半径为2,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH,交OA于点H,设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,线段BI的最小值为 .
20.如图,Rt△ABC中,∠BAC=90°,AC=6,AB=8,O为Rt△ABC的外心,I为Rt△ABC的内心,延长AI交⊙O于点D.连接OI,则cos∠OID 的值为 .
三、解答题
21.如图,在菱形中,对角线,相交于点E,经过A,D两点,交对角线于点F,连接交于点G,且.
(1)求证:是的切线;
(2)已知的半径与菱形的边长之比为,求的值.
22.在矩形ABCD中,AB=2,BC=1,以AB为直径的半圆切CD于E,P为CD上的动点(不与C、D重合),连结AP交半圆于F,连结BP、BF,如图甲所示.
(1)当时,图甲中有几对全等的三角形?将其表示出来.
(2)P点在CD上移动,还有能构成全等三角形的情况吗?若有,请说出还有几次,并在图乙中用尺规作出每次构成全等三角形时的图形(不写作法,保留作图痕迹);若没有,说明理由.
23.如图,圆的内接五边形ABCDE中,AD和BE交于点N,AB和EC的延长线交于点M,CD∥BE,BC∥AD,BM=BC=1,点D是的中点.
(1)求证:BC=DE;
(2)求证:AE是圆的直径;
(3)求圆的面积.
24.如图,△ABC内接于⊙O,点D在⊙O外,∠ADC=90°,BD交⊙O于点E,交AC于点F,∠EAC=∠DCE,∠CEB=∠DCA,CD=6,AD=8.
(1)求证:AB∥CD;
(2)求证:CD是⊙O的切线;
(3)求tan∠ACB的值.
25.定义:如果一个三角形中有两个内角α,β,满足α+2β=90°,那么我们称这个三角形为“近直角三角形”.
(1)若△ABC是“近直角三角形”,∠B>90°,∠C=50°,则∠A= °;
(2)如图,在Rt△ABC中,∠ACB=90°,点O为AB边上一点,以OB为半径的圆与AC相切于点D,连接BD.求证:△ABD是“近直角三角形”.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列命题中错误的有( )
①平分弦的直径垂直于弦,并且平分弦所对的两条弧;
②在同圆或等圆中,相等的圆心角所对的弧相等;
③三个点确定一个圆
④反比例函数的图像在一、三象限,y随x的增大而减小
⑤三角形的内心到各边的距离相等,三角形的外心是三条边垂直平分线的交点
A.1个 B.2个 C.3个 D.4个
2.如图,的顶点是上的一个动点,,,边,分别交于点,,分别过点,作的切线交于点,且点恰好在边上,连接,若的半径为,则的最大值为( )
A. B. C. D.
3.如图,点是的内心,,,,于点,则的长为( )
A.2 B.4 C.5 D.6.
4.如图,AB是⊙O的弦,AC是⊙O的直径,将沿着AB弦翻折,恰好经过圆心O.若⊙O的半径为6,则图中阴影部分的面积等于( )
A.6π B.9 C.9π D.6
5.如图,已知PA、PB切⊙O于A、B两点,CD切⊙O于E,△PCD的周长为20,∠P=60°,则⊙O的半径( )
A.4 B.5 C.5 D.
6.如图,PA、PB是的两条切线,切点分别为A、B连接OA、OB、AB、PO,PO与AB交于点C,若,,则PO的长为( )
A.12 B.8 C. D.4
7.如图,半径为2的与x轴的正半轴交于点A,点B是上一动点,点C为弦的中点,直线与x轴、y轴分别交于点D、E,则面积的最小值为( )
A.1 B. C.3 D.2
8.如图,的半径为,点、、、在上,且四边形是矩形,点是劣弧上一动点,、分别与相交于点、点.当且时,的长度为( )
A. B. C. D.
9.下列说法正确的是( )
A.任意三点可以确定一个圆
B.平分弦的直径垂直于弦,并且平分该弦所对的弧
C.同一平面内,点P到⊙O上一点的最小距离为2,最大距离为8,则该圆的半径为5
D.同一平面内,点P到圆心O的距离为5,且圆的半径为10,则过点P且长度为整数的弦共有5条
10.如图,切于点切于点交于点,下列结论中不一定成立的是( )
A. B.平分
C. D.
二、填空题
11.如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交于点E,以点O为圆心,OC的长为半径作交OB于点D,若OA=2,则阴影部分的面积为 .
12.如图,为的直径,点在的延长线上,,与相切,切点分别为,.若,,则
13.三边长分别是5cm,12cm,13cm的三角形的内切圆半径为 cm.
14.如图,已知为的直径,、为的切线,、为切点,交于点,的延长线交于点,连接、.给出以下结论:①;②;③点为的内心.其中正确的是 (填序号).
15.如图,∠ACB=60°,半径为3cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是 cm.
16.如图,在直角坐标系中,已知点A(6,0),B(6,),C(0,),点P为平面内一点,连接BP,OP,CP,且,则CP的最小值为 .
17.如图,在平面直角坐标系中,⊙P的半径为5,圆心P坐标是(5,a)(a>5),函数y=x的图象被⊙P截得的弦AB的长为4,则a的值是 .
18.已知O,I分别是△ABC的外心和内心,∠BOC=140°,则∠BIC的大小是 .
19.如图,半径为2,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH,交OA于点H,设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,线段BI的最小值为 .
20.如图,Rt△ABC中,∠BAC=90°,AC=6,AB=8,O为Rt△ABC的外心,I为Rt△ABC的内心,延长AI交⊙O于点D.连接OI,则cos∠OID 的值为 .
三、解答题
21.如图,在菱形中,对角线,相交于点E,经过A,D两点,交对角线于点F,连接交于点G,且.
(1)求证:是的切线;
(2)已知的半径与菱形的边长之比为,求的值.
22.在矩形ABCD中,AB=2,BC=1,以AB为直径的半圆切CD于E,P为CD上的动点(不与C、D重合),连结AP交半圆于F,连结BP、BF,如图甲所示.
(1)当时,图甲中有几对全等的三角形?将其表示出来.
(2)P点在CD上移动,还有能构成全等三角形的情况吗?若有,请说出还有几次,并在图乙中用尺规作出每次构成全等三角形时的图形(不写作法,保留作图痕迹);若没有,说明理由.
23.如图,圆的内接五边形ABCDE中,AD和BE交于点N,AB和EC的延长线交于点M,CD∥BE,BC∥AD,BM=BC=1,点D是的中点.
(1)求证:BC=DE;
(2)求证:AE是圆的直径;
(3)求圆的面积.
24.如图,△ABC内接于⊙O,点D在⊙O外,∠ADC=90°,BD交⊙O于点E,交AC于点F,∠EAC=∠DCE,∠CEB=∠DCA,CD=6,AD=8.
(1)求证:AB∥CD;
(2)求证:CD是⊙O的切线;
(3)求tan∠ACB的值.
25.定义:如果一个三角形中有两个内角α,β,满足α+2β=90°,那么我们称这个三角形为“近直角三角形”.
(1)若△ABC是“近直角三角形”,∠B>90°,∠C=50°,则∠A= °;
(2)如图,在Rt△ABC中,∠ACB=90°,点O为AB边上一点,以OB为半径的圆与AC相切于点D,连接BD.求证:△ABD是“近直角三角形”.
