5.1 相交线同步课堂一讲一练(练)(含解析)
文档属性
| 名称 | 5.1 相交线同步课堂一讲一练(练)(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 16:09:17 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
七下同步课堂一讲一练
5.1 相交线
基础训练
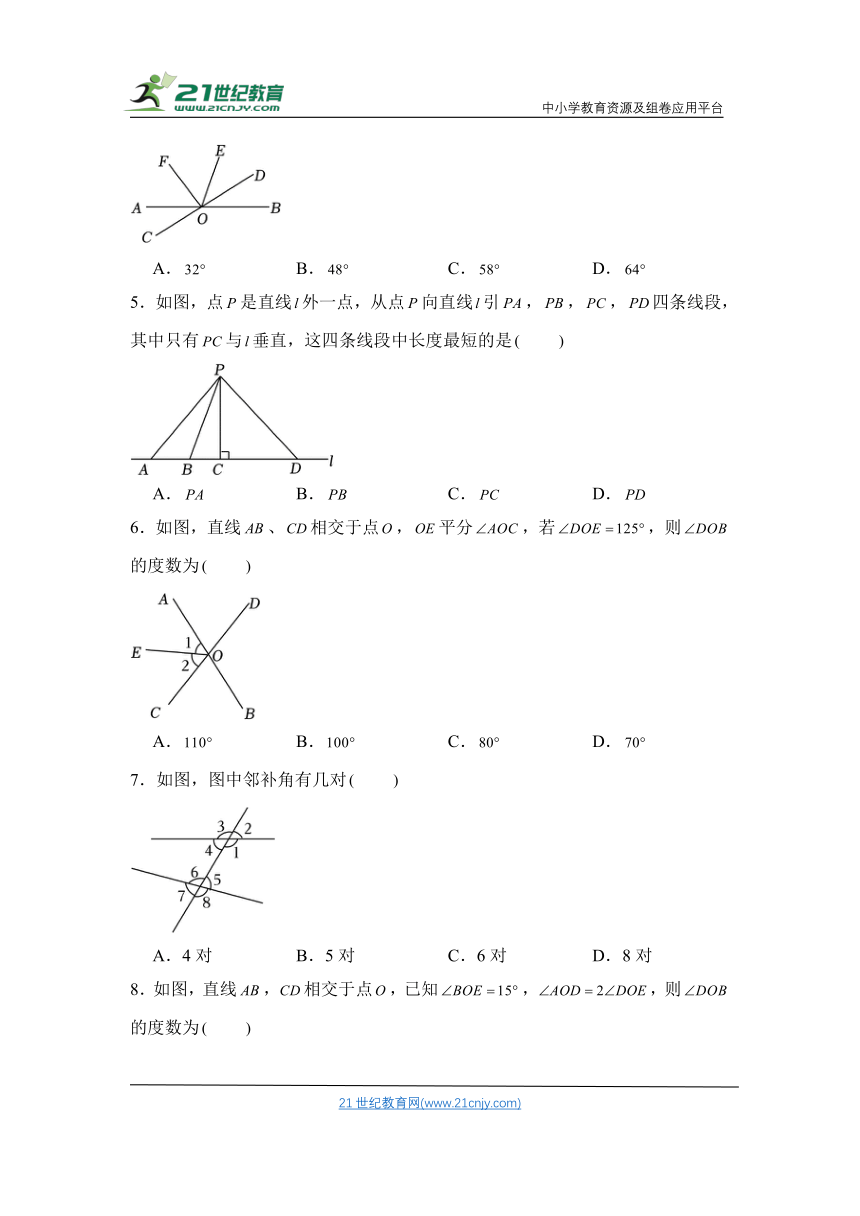
一、选择题
1.下列选项中,和是对顶角的是
A. B. C. D.
2.图中,和是同位角的是
A. B. C. D.
3.如图,测量运动员跳远成绩选取的是的长度,其依据是
A.两点确定一条直线 B.两点之间直线最短
C.两点之间线段最短 D.垂线段最短
4.如图,直线、相交于点,,平分,若,则的度数为
A. B. C. D.
5.如图,点是直线外一点,从点向直线引,,,四条线段,其中只有与垂直,这四条线段中长度最短的是
A. B. C. D.
6.如图,直线、相交于点,平分,若,则的度数为
A. B. C. D.
7.如图,图中邻补角有几对
A.4对 B.5对 C.6对 D.8对
8.如图,直线,相交于点,已知,,则的度数为
A. B. C. D.
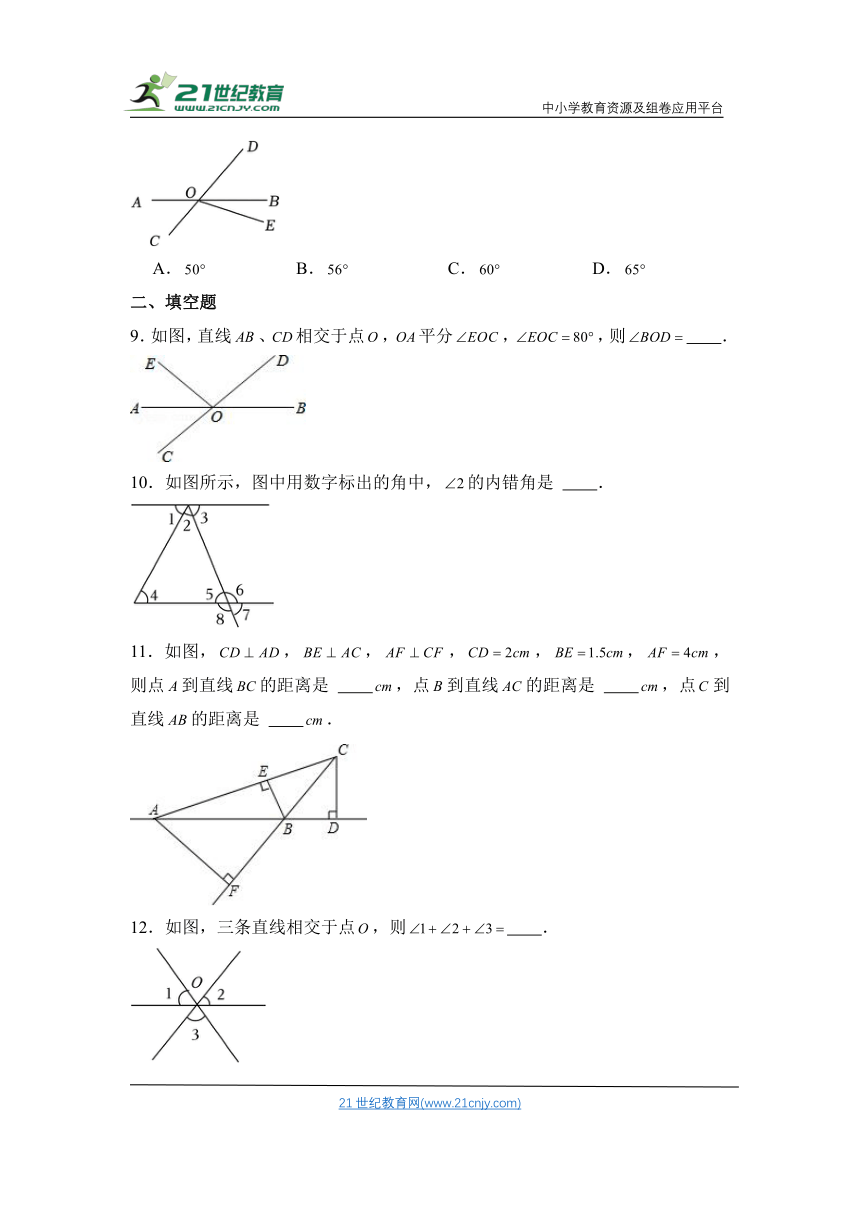
二、填空题
9.如图,直线、相交于点,平分,,则 .
10.如图所示,图中用数字标出的角中,的内错角是 .
11.如图,,,,,,,则点到直线的距离是 ,点到直线的距离是 ,点到直线的距离是 .
12.如图,三条直线相交于点,则 .
13.如图,两条直线,相交,,则 .
三、解答题
14.如图,图中所标出的,,,,中,哪两个角是同位角?哪两个角是内错角?哪两个角是同旁内角?
15.如图,,平分,,求的大小.
16.如图,直线,相交于点,平分,于点,若,求的大小.
17.如图:已知直线、相交于,,若,求的度数.
18.如图,直线、相交于点,,垂足为,.
(1)求的度数;
(2)若平分,求,的度数.
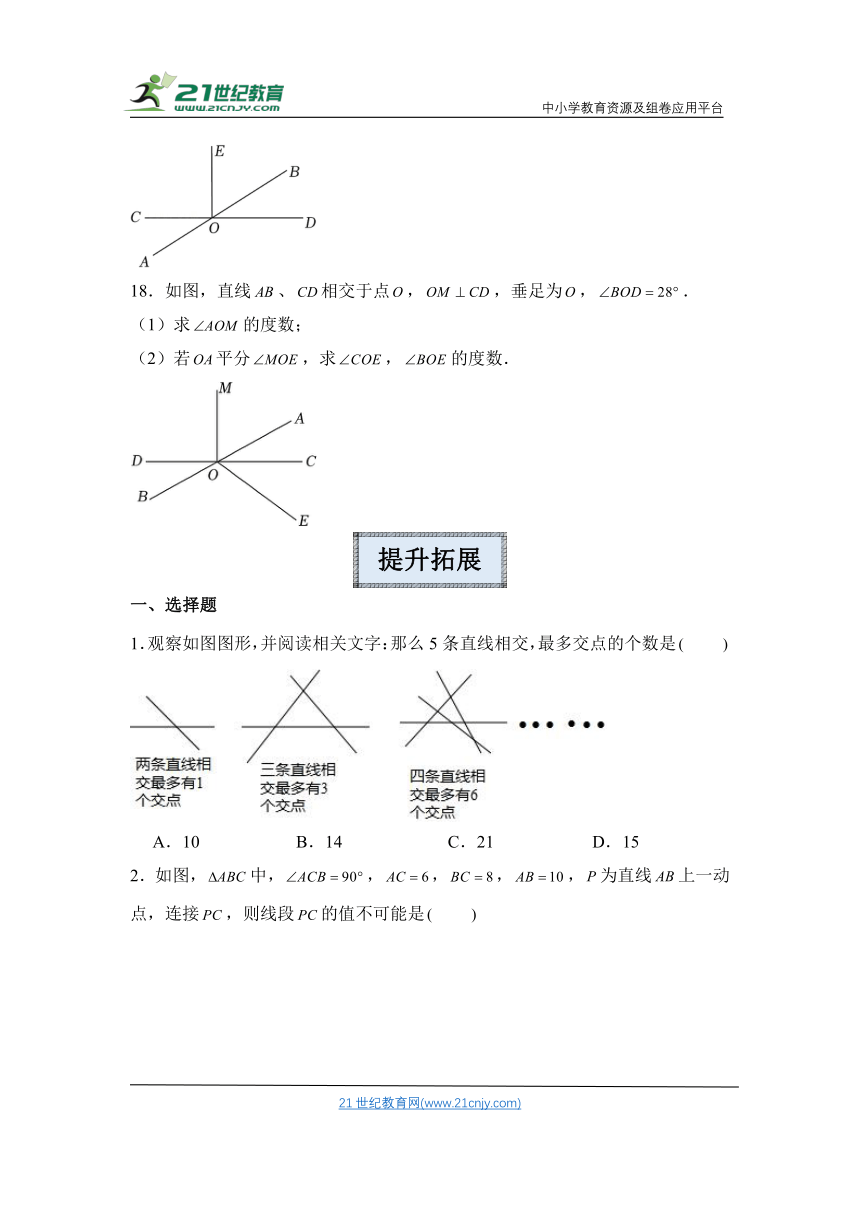
提升拓展
一、选择题
1.观察如图图形,并阅读相关文字:那么5条直线相交,最多交点的个数是
A.10 B.14 C.21 D.15
2.如图,中,,,,,为直线上一动点,连接,则线段的值不可能是
A.4.8 B.6 C.4 D.5
3.如图,直线、被直线和所截,下列说法正确的是
A.与是同旁内角 B.与是同位角
C.与是内错角 D.与是同旁内角
4.如图,直线,交于点,平分,,平分,若,则等于
A. B. C. D.
5.如图,的邻补角是
A. B.和 C. D.和
二、填空题
6.如图,与相交于点,若,,则 .
7.如图,直线,相交于点,,垂足为,且平分.
(1)若,则的度数为 ;
(2)与的数量关系为 .
8.如图,直线,相交于点,平分,且,则的度数是 .
9.如图,点在直线上,于,平分,平分,则的度数为 .
三、解答题
10.如图,已知直线,被直线,所截,直线,,相交于点,按要求完成下列各小题.
(1)在图中的这9个角中,同位角共有多少对?请你全部写出来;
(2)和是什么位置关系的角?和之间的位置关系与和的相同吗?
11.如图,直线,相交于点,平分,.
(1)若,求的度数;
(2)猜想与之间的位置关系,并证明.
12.如图所示,直线,相交于点,平分,射线在内部.
(1)若,求的度数.
(2)若,求的度数.
真题在线
一、选择题
1.数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示
A.同旁内角、同位角、内错角 B.同位角、内错角、对顶角
C.对顶角、同位角、同旁内角 D.同位角、内错角、同旁内角
2.如图,利用工具测量角,则的大小为
A. B. C. D.
3.如图,直线,被直线所截,下列各组角是同位角的是
A.与 B.与 C.与 D.与
4.如图,直线,相交于点,,垂足为.若,则的度数为
A. B. C. D.
5.如图,直线、相交于点,若,则的度数是
A. B. C. D.
6.如图,直线与相交于点,,,则的度数是
A. B. C. D.
7.如图,与是内错角的是
A. B. C. D.
8.如图,设点是直线外一点,,垂足为点,点是直线上的一个动点,连结,则
A. B. C. D.
9.如图,在平面内作已知直线的垂线,可作垂线的条数有
A.0条 B.1条 C.2条 D.无数条
二、填空题
10.如图,直线,相交于点,,则 .
11.如图,与相交于点,是的平分线,且恰好平分,则 度.
12.如图,3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,按照这样的规律,则20条直线两两相交最多有 个交点.
13.如图,某单位要在河岸上建一个水泵房引水到处.他们的做法是:过点作于点,将水泵房建在了处.这样做最节省水管长度,其数学道理是 .
基础训练
1.解:对顶角的定义:两条直线相交后所得,有公共顶点且两边互为反向延长线的两个角叫做对顶角,观察选项,只有选项符合,
故选:.
2.解:、和不是同位角,故不符合题意;
、和不是同位角,故不符合题意;
、和不是同位角,故不符合题意;
、和是同位角,故符合题意.
故选:.
3.解:该运动员跳远成绩的依据是:垂线段最短;
故选:.
4.解:,,
,
平分,
.
,
.
故选:.
5.解:点是直线外一点,从点向直线引,,,四条线段,其中只有与垂直,这四条线段中长度最短的是.
故选:.
6.解:,
,
平分,
,
.
故选:.
7.解:与是邻补角,与是邻补角,与是邻补角,与是邻补角,与是邻补角,与是邻补角,与是邻补角,与是邻补角共8对,
故选:.
8.解:设,
则,
由题意得:,
解得:,
,
故选:.
9.解:平分,,
,
.
故答案为:.
10.解:图中用数字标出的角中,的内错角是.
故答案为:.
11.解:,,,,,,
点到直线的距离是,点到直线的距离是,点到直线的距离是.
故答案为:4、1.5、2.
12.解:根据对顶角相等,可得,
由平角的定义,可得,
,
故答案为:.
13.解:,与是邻补角,
,即,
,
由邻补角的定义得.
故答案为:.
14.解:与,与是同位角;
与,与是内错角;
与,与是同旁内角.
15.解:,
,
又,
,
平分,
,
,
即.
16.解:,
,
,
,
平分,
,
.
17.解:,,
,
,
.
18.解:(1),
,
,
;
(2)平分,
,
,
,
.
提升拓展
1.解:两条直线相交,最多交点数为1个;
三条直线相交,最多交点数为(个;
四条直线相交,最多交点数为(个;
五条直线相交,最多交点数为(个.
故选:.
2.解:在中,,,,,
当时,的值最小,
此时:,
.
线段的值不可能是4,
故选:.
3.解:、与是内错角,错误;
、与不是同位角,错误;
、与不是同旁内角,错误;
、与是同旁内角,正确;
故选:.
4.解:,
,
平分,
,
,
,
平分,
,
,
故选:.
5.解:因为构成的两边与射线和有关;
从射线来看,的邻补角是,
从射线来看,的邻补角是,
的邻补角有,,
故选:.
6.解:,
,
,
,
,
故答案为:.
7.解:(1),
,
,,
,
平分,
,
,
.
故答案为:;
(2),,
,
,
,
.
故答案为:.
8.解:,
.
平分,
.
与是对顶角,
.
故答案为:65.
9.解:于,,
,
平分,平分,
,,
.
故答案为:.
10.解:(1)如图所示:同位角共有5对:
分别是和,和,和,和,和;
(2)和是同旁内角,和也是同旁内角,故和之间的位置关系与和的相同.
11.解:(1),
,
平分,
,
,
即;
(2),
证明:设,则,
,
,
又平分,
,
又,
,
,
即.
12.解:(1)直线、相交于点,
,
,
平分,
,
;
(2)平分,
,
,
,
,,
,
.
真题在线
一、选择题
1.解:根据同位角、内错角、同旁内角的概念,可知
第一个图是同位角,第二个图是内错角,第三个图是同旁内角.
故选:.
2.解:根据对顶角相等的性质,可得:,
故选:.
3.解:根据同位角、邻补角、对顶角的定义进行判断,
、和是对顶角,故错误;
、和是同位角,故正确;
、和是内错角,故错误;
、和是邻补角,故错误.
故选:.
4.解:,
,
,
.
故选:.
5.解:,与是对顶角,
.
故选:.
6.解:,
.
,,
.
故选:.
7.解:根据内错角的定义,的内错角是.
故选:.
8.解:,点是直线上的一个动点,连结,
,
故选:.
9.解:在同一平面内,与已知直线垂直的直线有无数条,
所以作已知直线的垂线,可作无数条.
故选:.
二、填空题
10.解:和是一对顶角,
.
故答案为:70.
11.解:是的平分线,恰好平分,
,,
,
,
,
,
故答案为:60.
12.解:2条直线相交有1个交点,
3条直线相交最多有个交点,
4条直线相交最多有个交点,
条直线相交最多有个交点,
条直线相交最多有190个交点.
故答案为190.
13.解:过点作于点,将水泵房建在了处.这样做最节省水管长度,其数学道理是垂线段最短.
故答案为:垂线段最短.
21世纪教育网(www.21cnjy.com)
七下同步课堂一讲一练
5.1 相交线
基础训练
一、选择题
1.下列选项中,和是对顶角的是
A. B. C. D.
2.图中,和是同位角的是
A. B. C. D.
3.如图,测量运动员跳远成绩选取的是的长度,其依据是
A.两点确定一条直线 B.两点之间直线最短
C.两点之间线段最短 D.垂线段最短
4.如图,直线、相交于点,,平分,若,则的度数为
A. B. C. D.
5.如图,点是直线外一点,从点向直线引,,,四条线段,其中只有与垂直,这四条线段中长度最短的是
A. B. C. D.
6.如图,直线、相交于点,平分,若,则的度数为
A. B. C. D.
7.如图,图中邻补角有几对
A.4对 B.5对 C.6对 D.8对
8.如图,直线,相交于点,已知,,则的度数为
A. B. C. D.
二、填空题
9.如图,直线、相交于点,平分,,则 .
10.如图所示,图中用数字标出的角中,的内错角是 .
11.如图,,,,,,,则点到直线的距离是 ,点到直线的距离是 ,点到直线的距离是 .
12.如图,三条直线相交于点,则 .
13.如图,两条直线,相交,,则 .
三、解答题
14.如图,图中所标出的,,,,中,哪两个角是同位角?哪两个角是内错角?哪两个角是同旁内角?
15.如图,,平分,,求的大小.
16.如图,直线,相交于点,平分,于点,若,求的大小.
17.如图:已知直线、相交于,,若,求的度数.
18.如图,直线、相交于点,,垂足为,.
(1)求的度数;
(2)若平分,求,的度数.
提升拓展
一、选择题
1.观察如图图形,并阅读相关文字:那么5条直线相交,最多交点的个数是
A.10 B.14 C.21 D.15
2.如图,中,,,,,为直线上一动点,连接,则线段的值不可能是
A.4.8 B.6 C.4 D.5
3.如图,直线、被直线和所截,下列说法正确的是
A.与是同旁内角 B.与是同位角
C.与是内错角 D.与是同旁内角
4.如图,直线,交于点,平分,,平分,若,则等于
A. B. C. D.
5.如图,的邻补角是
A. B.和 C. D.和
二、填空题
6.如图,与相交于点,若,,则 .
7.如图,直线,相交于点,,垂足为,且平分.
(1)若,则的度数为 ;
(2)与的数量关系为 .
8.如图,直线,相交于点,平分,且,则的度数是 .
9.如图,点在直线上,于,平分,平分,则的度数为 .
三、解答题
10.如图,已知直线,被直线,所截,直线,,相交于点,按要求完成下列各小题.
(1)在图中的这9个角中,同位角共有多少对?请你全部写出来;
(2)和是什么位置关系的角?和之间的位置关系与和的相同吗?
11.如图,直线,相交于点,平分,.
(1)若,求的度数;
(2)猜想与之间的位置关系,并证明.
12.如图所示,直线,相交于点,平分,射线在内部.
(1)若,求的度数.
(2)若,求的度数.
真题在线
一、选择题
1.数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示
A.同旁内角、同位角、内错角 B.同位角、内错角、对顶角
C.对顶角、同位角、同旁内角 D.同位角、内错角、同旁内角
2.如图,利用工具测量角,则的大小为
A. B. C. D.
3.如图,直线,被直线所截,下列各组角是同位角的是
A.与 B.与 C.与 D.与
4.如图,直线,相交于点,,垂足为.若,则的度数为
A. B. C. D.
5.如图,直线、相交于点,若,则的度数是
A. B. C. D.
6.如图,直线与相交于点,,,则的度数是
A. B. C. D.
7.如图,与是内错角的是
A. B. C. D.
8.如图,设点是直线外一点,,垂足为点,点是直线上的一个动点,连结,则
A. B. C. D.
9.如图,在平面内作已知直线的垂线,可作垂线的条数有
A.0条 B.1条 C.2条 D.无数条
二、填空题
10.如图,直线,相交于点,,则 .
11.如图,与相交于点,是的平分线,且恰好平分,则 度.
12.如图,3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,按照这样的规律,则20条直线两两相交最多有 个交点.
13.如图,某单位要在河岸上建一个水泵房引水到处.他们的做法是:过点作于点,将水泵房建在了处.这样做最节省水管长度,其数学道理是 .
基础训练
1.解:对顶角的定义:两条直线相交后所得,有公共顶点且两边互为反向延长线的两个角叫做对顶角,观察选项,只有选项符合,
故选:.
2.解:、和不是同位角,故不符合题意;
、和不是同位角,故不符合题意;
、和不是同位角,故不符合题意;
、和是同位角,故符合题意.
故选:.
3.解:该运动员跳远成绩的依据是:垂线段最短;
故选:.
4.解:,,
,
平分,
.
,
.
故选:.
5.解:点是直线外一点,从点向直线引,,,四条线段,其中只有与垂直,这四条线段中长度最短的是.
故选:.
6.解:,
,
平分,
,
.
故选:.
7.解:与是邻补角,与是邻补角,与是邻补角,与是邻补角,与是邻补角,与是邻补角,与是邻补角,与是邻补角共8对,
故选:.
8.解:设,
则,
由题意得:,
解得:,
,
故选:.
9.解:平分,,
,
.
故答案为:.
10.解:图中用数字标出的角中,的内错角是.
故答案为:.
11.解:,,,,,,
点到直线的距离是,点到直线的距离是,点到直线的距离是.
故答案为:4、1.5、2.
12.解:根据对顶角相等,可得,
由平角的定义,可得,
,
故答案为:.
13.解:,与是邻补角,
,即,
,
由邻补角的定义得.
故答案为:.
14.解:与,与是同位角;
与,与是内错角;
与,与是同旁内角.
15.解:,
,
又,
,
平分,
,
,
即.
16.解:,
,
,
,
平分,
,
.
17.解:,,
,
,
.
18.解:(1),
,
,
;
(2)平分,
,
,
,
.
提升拓展
1.解:两条直线相交,最多交点数为1个;
三条直线相交,最多交点数为(个;
四条直线相交,最多交点数为(个;
五条直线相交,最多交点数为(个.
故选:.
2.解:在中,,,,,
当时,的值最小,
此时:,
.
线段的值不可能是4,
故选:.
3.解:、与是内错角,错误;
、与不是同位角,错误;
、与不是同旁内角,错误;
、与是同旁内角,正确;
故选:.
4.解:,
,
平分,
,
,
,
平分,
,
,
故选:.
5.解:因为构成的两边与射线和有关;
从射线来看,的邻补角是,
从射线来看,的邻补角是,
的邻补角有,,
故选:.
6.解:,
,
,
,
,
故答案为:.
7.解:(1),
,
,,
,
平分,
,
,
.
故答案为:;
(2),,
,
,
,
.
故答案为:.
8.解:,
.
平分,
.
与是对顶角,
.
故答案为:65.
9.解:于,,
,
平分,平分,
,,
.
故答案为:.
10.解:(1)如图所示:同位角共有5对:
分别是和,和,和,和,和;
(2)和是同旁内角,和也是同旁内角,故和之间的位置关系与和的相同.
11.解:(1),
,
平分,
,
,
即;
(2),
证明:设,则,
,
,
又平分,
,
又,
,
,
即.
12.解:(1)直线、相交于点,
,
,
平分,
,
;
(2)平分,
,
,
,
,,
,
.
真题在线
一、选择题
1.解:根据同位角、内错角、同旁内角的概念,可知
第一个图是同位角,第二个图是内错角,第三个图是同旁内角.
故选:.
2.解:根据对顶角相等的性质,可得:,
故选:.
3.解:根据同位角、邻补角、对顶角的定义进行判断,
、和是对顶角,故错误;
、和是同位角,故正确;
、和是内错角,故错误;
、和是邻补角,故错误.
故选:.
4.解:,
,
,
.
故选:.
5.解:,与是对顶角,
.
故选:.
6.解:,
.
,,
.
故选:.
7.解:根据内错角的定义,的内错角是.
故选:.
8.解:,点是直线上的一个动点,连结,
,
故选:.
9.解:在同一平面内,与已知直线垂直的直线有无数条,
所以作已知直线的垂线,可作无数条.
故选:.
二、填空题
10.解:和是一对顶角,
.
故答案为:70.
11.解:是的平分线,恰好平分,
,,
,
,
,
,
故答案为:60.
12.解:2条直线相交有1个交点,
3条直线相交最多有个交点,
4条直线相交最多有个交点,
条直线相交最多有个交点,
条直线相交最多有190个交点.
故答案为190.
13.解:过点作于点,将水泵房建在了处.这样做最节省水管长度,其数学道理是垂线段最短.
故答案为:垂线段最短.
21世纪教育网(www.21cnjy.com)
