19.2 证明举例—用普通语言叙述的几何命题的证明(第7课时)课件(共18张PPT)-2023-2024学年八年级数学上册同步精品课堂(沪教版)
文档属性
| 名称 | 19.2 证明举例—用普通语言叙述的几何命题的证明(第7课时)课件(共18张PPT)-2023-2024学年八年级数学上册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
沪教版八年级上册
第18章 正比例函数与反比例函数
19.2 证明举例—用普通语言叙述的几何命题的证明(第7课时)
目 录
1 学习目标
2 新课讲解
3 课本例题
4 课本练习
6 随堂检测
7 课堂小结
5 题型讲解
学习目标
经历添加辅助线进行演绎推理的过程,了解旋转在几何证明中的运用,进一步获得探究证题思路的经历,丰富演绎证明的经验,体会在图形运动思想的指导下添置辅助线的方法和构造基本图形的方法。
初步掌握演绎推理的规范表达,发展逻辑思维和演绎推理的能力。
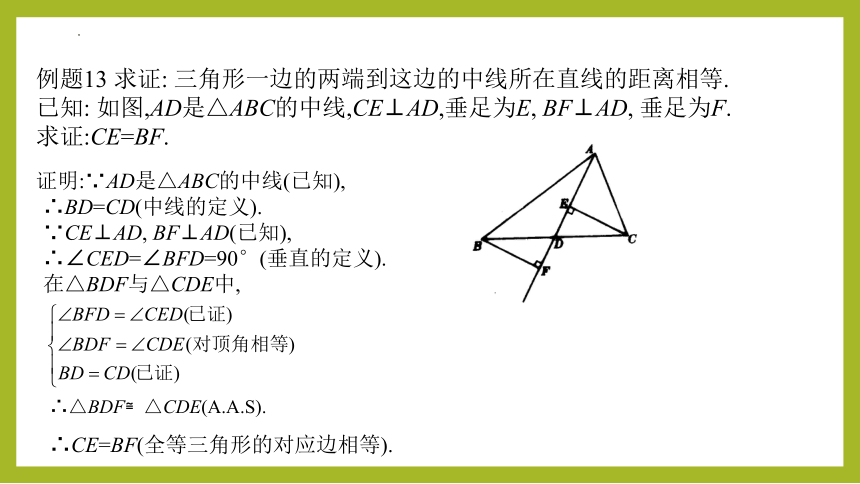
例题13 求证: 三角形一边的两端到这边的中线所在直线的距离相等.
已知: 如图,AD是△ABC的中线,CE⊥AD,垂足为E, BF⊥AD, 垂足为F.
求证:CE=BF.
证明:∵AD是△ABC的中线(已知),
∴BD=CD(中线的定义).
∵CE⊥AD, BF⊥AD(已知),
∴∠CED=∠BFD=90°(垂直的定义).
在△BDF与△CDE中,
∴△BDF≌△CDE(A.A.S).
∴CE=BF(全等三角形的对应边相等).
例题14 求证:有两边及其中一边上的中线对应相等的两个三角形全等.
已知:如图,在△ABC与△A’B’C’中,AD、A’D’分别是BC、B’C’上的中线,
AB=A’B’,BC=B’C’,AD=A’D’.
求证:△ABC≌△A’B’C’.
又∵BC=B’C’(已知),
∴BD=B’D’(等式性质).
在△ABD与△A’B’D’中,
AB=A’B’(已知)
BD=B’D’(已证),
AD=A’D’(已知),
∴△ABD≌△A’B’D’ (S.S.S).
得∠B=∠B′(全等三角形的对应角相等).
在△ABC与△A’B’C’中
AB=A’B’(已知)
∠B=∠B’(已证),
BC=B’C’(已知)
∴△ABC≌△A’B’C’ (S.A.S)
例题14 求证:有两边及其中一边上的中线对应相等的两个三角形全等.
已知:如图,在△ABC与△A’B’C’中,AD、A’D’分别是BC、B’C’上的中线,
AB=A’B’,BC=B’C’,AD=A’D’.
求证:△ABC≌△A’B’C’.
课本练习
已知:如图,在 △ABC 与 △A'B'C 中,AB = A′B′,AC = A′C′,CD,C'D' 分别是 △ABC,△A'B'C' 的中线,且 CD = C′D'.
求证:△ABC ≌ △A'B′C′.
证明:∵ AB = A'B',CD,CD' 分别是 △ABC,△A'B′C′ 的中线,
∴ AB = A′B′,即 AD = A′D′.
1.证明:如果两个三角形有两条边和其中一边上的中线分别相等,那么这两个三角形全等.
随堂检测
在 △ADC 与 △A'D'C′ 中,
∴ △ADC ≌ △A′D′C′ (SSS).
∴∠A = ∠A′.
在 △ABC 与 △A'B′C′ 中,
∴△ABC ≌ △A'B′C′ (SAS).
1.证明:如果两个三角形有两条边和其中一边上的中线分别相等,那么这两小三角形全等.
2.求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知: 如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.
证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).
又∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边).
A
B
C
E
(
(
1
2
D
3.证明:两条平行线的一组同旁内角的平分线互相垂直.4.求证:全等三角形对应边的高相等.
已知:如图,△ABC ≌△A′B′C′ ,AD,A′ D′ 分别是△ABC 和△A′B′C′的高.求证:AD= A′D′ .
A
B
C
D
A ′
B ′
C ′
D ′
文字命题证明
需要画图,
写出已知和求证
分析:从图中可以看出,AD、A'D'分别属于△ABD与△A'B'D',
要证AD = A'D',只需证明这两个三角形全等即可.
证明: ∵ △ABC≌△A′B′C′ (已知),
∴ AB=A′B′(全等三角形的对应边相等),
∵∠ B= ∠B′ (全等三角形的对应角相等).
在△ABD和△A′B′D′中,
∵
∴ △ABD≌△A′B′D′(A.A.S)
∴AD = A′D′ (全等三角形的对应边相等).
∠ADB=∠A′D′B′ = 90 °(已知),
∠B=∠B′ (已证),
AB=A′B′(已证),
于此类似,你能说明全等三角形对应边上的中线、对应角的平分线又有什么关系呢?
A
B
C
5.求证三个角都相等的三角形是等边三角形.
已知:如图,∠A= ∠ B=∠C.
求证: AB=AC=BC.
∵ ∠A= ∠B,
∴ AC=BC.
∵ ∠B=∠C,
∴ AB=AC.
∴AB=AC=BC.
证明:
6.求证:有一个角是60°的等腰三角形是等边三角形
已知: 若AB=AC, ∠A= 60°.
求证: AB=AC=BC.
证明:∵AB=AC , ∠A= 60 °.
∴∠B=∠C= (180°-∠A)= 60°.
∴∠A= ∠B=∠C.
∴AB=AC=BC.
A
B
C
7.求证:如果一个三角形两边上的高相等,那么这个三角形是等腰三角形.
课堂小结:
1.一般地当遇到三角形一边的中线(或中点) 的有关问题时,往往考虑利用图形的旋转,构造全等三角形来添加辅助线.
2.利用图形的旋转运动可以把分散的已知条件集中起来, 从而找到添加辅助线的方法,解决问题.
沪教版八年级上册
第18章 正比例函数与反比例函数
19.2 证明举例—用普通语言叙述的几何命题的证明(第7课时)
目 录
1 学习目标
2 新课讲解
3 课本例题
4 课本练习
6 随堂检测
7 课堂小结
5 题型讲解
学习目标
经历添加辅助线进行演绎推理的过程,了解旋转在几何证明中的运用,进一步获得探究证题思路的经历,丰富演绎证明的经验,体会在图形运动思想的指导下添置辅助线的方法和构造基本图形的方法。
初步掌握演绎推理的规范表达,发展逻辑思维和演绎推理的能力。
例题13 求证: 三角形一边的两端到这边的中线所在直线的距离相等.
已知: 如图,AD是△ABC的中线,CE⊥AD,垂足为E, BF⊥AD, 垂足为F.
求证:CE=BF.
证明:∵AD是△ABC的中线(已知),
∴BD=CD(中线的定义).
∵CE⊥AD, BF⊥AD(已知),
∴∠CED=∠BFD=90°(垂直的定义).
在△BDF与△CDE中,
∴△BDF≌△CDE(A.A.S).
∴CE=BF(全等三角形的对应边相等).
例题14 求证:有两边及其中一边上的中线对应相等的两个三角形全等.
已知:如图,在△ABC与△A’B’C’中,AD、A’D’分别是BC、B’C’上的中线,
AB=A’B’,BC=B’C’,AD=A’D’.
求证:△ABC≌△A’B’C’.
又∵BC=B’C’(已知),
∴BD=B’D’(等式性质).
在△ABD与△A’B’D’中,
AB=A’B’(已知)
BD=B’D’(已证),
AD=A’D’(已知),
∴△ABD≌△A’B’D’ (S.S.S).
得∠B=∠B′(全等三角形的对应角相等).
在△ABC与△A’B’C’中
AB=A’B’(已知)
∠B=∠B’(已证),
BC=B’C’(已知)
∴△ABC≌△A’B’C’ (S.A.S)
例题14 求证:有两边及其中一边上的中线对应相等的两个三角形全等.
已知:如图,在△ABC与△A’B’C’中,AD、A’D’分别是BC、B’C’上的中线,
AB=A’B’,BC=B’C’,AD=A’D’.
求证:△ABC≌△A’B’C’.
课本练习
已知:如图,在 △ABC 与 △A'B'C 中,AB = A′B′,AC = A′C′,CD,C'D' 分别是 △ABC,△A'B'C' 的中线,且 CD = C′D'.
求证:△ABC ≌ △A'B′C′.
证明:∵ AB = A'B',CD,CD' 分别是 △ABC,△A'B′C′ 的中线,
∴ AB = A′B′,即 AD = A′D′.
1.证明:如果两个三角形有两条边和其中一边上的中线分别相等,那么这两个三角形全等.
随堂检测
在 △ADC 与 △A'D'C′ 中,
∴ △ADC ≌ △A′D′C′ (SSS).
∴∠A = ∠A′.
在 △ABC 与 △A'B′C′ 中,
∴△ABC ≌ △A'B′C′ (SAS).
1.证明:如果两个三角形有两条边和其中一边上的中线分别相等,那么这两小三角形全等.
2.求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知: 如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.
证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).
又∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边).
A
B
C
E
(
(
1
2
D
3.证明:两条平行线的一组同旁内角的平分线互相垂直.4.求证:全等三角形对应边的高相等.
已知:如图,△ABC ≌△A′B′C′ ,AD,A′ D′ 分别是△ABC 和△A′B′C′的高.求证:AD= A′D′ .
A
B
C
D
A ′
B ′
C ′
D ′
文字命题证明
需要画图,
写出已知和求证
分析:从图中可以看出,AD、A'D'分别属于△ABD与△A'B'D',
要证AD = A'D',只需证明这两个三角形全等即可.
证明: ∵ △ABC≌△A′B′C′ (已知),
∴ AB=A′B′(全等三角形的对应边相等),
∵∠ B= ∠B′ (全等三角形的对应角相等).
在△ABD和△A′B′D′中,
∵
∴ △ABD≌△A′B′D′(A.A.S)
∴AD = A′D′ (全等三角形的对应边相等).
∠ADB=∠A′D′B′ = 90 °(已知),
∠B=∠B′ (已证),
AB=A′B′(已证),
于此类似,你能说明全等三角形对应边上的中线、对应角的平分线又有什么关系呢?
A
B
C
5.求证三个角都相等的三角形是等边三角形.
已知:如图,∠A= ∠ B=∠C.
求证: AB=AC=BC.
∵ ∠A= ∠B,
∴ AC=BC.
∵ ∠B=∠C,
∴ AB=AC.
∴AB=AC=BC.
证明:
6.求证:有一个角是60°的等腰三角形是等边三角形
已知: 若AB=AC, ∠A= 60°.
求证: AB=AC=BC.
证明:∵AB=AC , ∠A= 60 °.
∴∠B=∠C= (180°-∠A)= 60°.
∴∠A= ∠B=∠C.
∴AB=AC=BC.
A
B
C
7.求证:如果一个三角形两边上的高相等,那么这个三角形是等腰三角形.
课堂小结:
1.一般地当遇到三角形一边的中线(或中点) 的有关问题时,往往考虑利用图形的旋转,构造全等三角形来添加辅助线.
2.利用图形的旋转运动可以把分散的已知条件集中起来, 从而找到添加辅助线的方法,解决问题.
