导数的概念(山西省大同市阳高县)
文档属性
| 名称 | 导数的概念(山西省大同市阳高县) |

|
|
| 格式 | rar | ||
| 文件大小 | 319.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-05 00:00:00 | ||
图片预览











文档简介
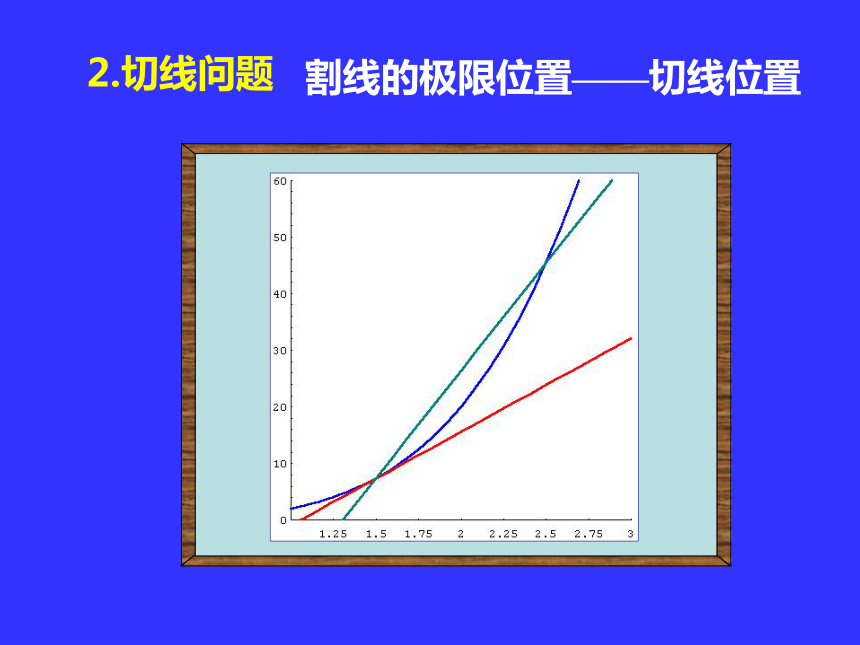
课件32张PPT。第二章 导数与微分 第一节 导数概念一、引例二、导数的定义三、导数的几何意义四、函数的可导性与连续性的关系一、引例1.自由落体运动的瞬时速度问题如图,如图, 让点 N 沿曲线 C 趋于M 时,割线 MN 的极限位置 MT,就称为曲线 C 在 M 点的切线.极限位置即比较两个公式 两个问题的共性:
所求量为函数增量与自变量增量之比的极限. 就定义为曲线上任意一点切线斜率的大小,它反映了该切线斜率就是函数值改变量对自变量改变量的变化率.类似问题还有:加速度是速度增量与时间增量之比的极限.
角速度是转角增量与时间增量之比的极限.
线密度是质量增量与长度增量之比的极限.
电流强度是电量增量与时间增量之比的极限.二、导数的定义 设函数 在点 的某个邻域内有定义? 如果极限存在,则称函数 在点 处可导,并称这个
极限为函数 在点 处的导数.记为 ,
即
1. 导数的定义.也可记作:注: 如果上述极限不存在,则称函数在点 处不可导.特别地,当时,则称函数 在点 处的导数为无穷大,此时,导数不存在.导数定义的其它表达形式函数在一点的导数是因变量在该点处的变化率,它反映了因变量随自变量的变化而变化的快慢程度.例1. 求函数 在点 处的导数.解 或 2. 导函数的定义.如果函数 在开区间I内的每点处都可导,就称函数 在开区间I内可导.这时,对于任一,都对应着 的一个确定的导数值.这样就构成了一个新的函数,这个函数叫做原来函数的导函数,简称导数.记作注: 导函数的定义式或函数 在某点 处的导数 与导函数 的区别与联系.区别: 是函数, 是数值.联系: 函数 在点 处的导数 就是导函数 在点 处的函数值,即:在以上两式中,虽然 可以取区间 内的任何数值,但在极限过程中, 是常量, 或 是变量.例2. 求函数 为常数)的导数.解 即 这就是说,常数的导数等于零. 例3. 求函数 的导数.解 即 例4. 求函数 的导数.解 即 例5. 求函数 (n为正整数)在 处的导数.解 即 更一般地 (其中 为常数)例6. 求函数 的导数.解 即 同理可得例7. 求函数 的导数.解 令即 特别地例8. 求函数 的导数.解 即 特别地特别地,特别地,以上得到的是部分基本初等函数的导数公式.3. 单侧导数.函数 在点 处的左导数函数 在点 处的右导数注: 导数与单侧导数的关系:函数 在点 处可导的充要条件是:左导数 和右导数 都存在且相等,即:如果函数 在开区间 内可导,且及 都存在,就说 在闭区间上可导.例9. 求函数 在 处的导数.解 函数 在 处不可导. 切线 法线 三、导数的几何意义函数 在点 处 的导数 在几何上表示曲线 在点处的切线的斜率,即( 为倾角) 切线方程为切线方程为例10. 求等边双曲线 在点( ,2)处的切线的斜率,并写出在该点处的切线方程和法线方程.解 ,所求切线即法线的斜率分别为, .所求切线方程为 ,即 .所求切线方程为 ,即 .例11. 求曲线 的通过点(0,-4)的切线方程.解 设切点为 ( , ) ,则切线的斜率为于是所求切线方程可设为把(0,-4)代入上式,得解之得故所求切线方程为即四、函数的可导性与连续性的关系如果函数 在点 处可导,则它在点 处连续.证明 函数 在点 处可导,(其中 ) 函数 在点 处连续.注: 函数 在点 处连续,但在点 处不一定可导.如果函数 在点 处不连续,则在点 处一定不可导.连续但不可导的例子例12. 函数 在区间 内连续,但在点 处不可导.这是因为:在点 处有函数 在点 处导数为无穷大,即导数不存在.例13. 函数 在区间 内连续,但在点处不可导.内容小结1.导数的实质:增量之比的极限.2.3.导数的几何意义:切线的斜率.4.可导必连续,但连续不一定可导.5.已学求导公式特别地,特别地,5.可导性的判断方法:(1) 不连续,一定不可导;(2) 直接用导数定义;(3) 看左右导数是否存在且相等.
所求量为函数增量与自变量增量之比的极限. 就定义为曲线上任意一点切线斜率的大小,它反映了该切线斜率就是函数值改变量对自变量改变量的变化率.类似问题还有:加速度是速度增量与时间增量之比的极限.
角速度是转角增量与时间增量之比的极限.
线密度是质量增量与长度增量之比的极限.
电流强度是电量增量与时间增量之比的极限.二、导数的定义 设函数 在点 的某个邻域内有定义? 如果极限存在,则称函数 在点 处可导,并称这个
极限为函数 在点 处的导数.记为 ,
即
1. 导数的定义.也可记作:注: 如果上述极限不存在,则称函数在点 处不可导.特别地,当时,则称函数 在点 处的导数为无穷大,此时,导数不存在.导数定义的其它表达形式函数在一点的导数是因变量在该点处的变化率,它反映了因变量随自变量的变化而变化的快慢程度.例1. 求函数 在点 处的导数.解 或 2. 导函数的定义.如果函数 在开区间I内的每点处都可导,就称函数 在开区间I内可导.这时,对于任一,都对应着 的一个确定的导数值.这样就构成了一个新的函数,这个函数叫做原来函数的导函数,简称导数.记作注: 导函数的定义式或函数 在某点 处的导数 与导函数 的区别与联系.区别: 是函数, 是数值.联系: 函数 在点 处的导数 就是导函数 在点 处的函数值,即:在以上两式中,虽然 可以取区间 内的任何数值,但在极限过程中, 是常量, 或 是变量.例2. 求函数 为常数)的导数.解 即 这就是说,常数的导数等于零. 例3. 求函数 的导数.解 即 例4. 求函数 的导数.解 即 例5. 求函数 (n为正整数)在 处的导数.解 即 更一般地 (其中 为常数)例6. 求函数 的导数.解 即 同理可得例7. 求函数 的导数.解 令即 特别地例8. 求函数 的导数.解 即 特别地特别地,特别地,以上得到的是部分基本初等函数的导数公式.3. 单侧导数.函数 在点 处的左导数函数 在点 处的右导数注: 导数与单侧导数的关系:函数 在点 处可导的充要条件是:左导数 和右导数 都存在且相等,即:如果函数 在开区间 内可导,且及 都存在,就说 在闭区间上可导.例9. 求函数 在 处的导数.解 函数 在 处不可导. 切线 法线 三、导数的几何意义函数 在点 处 的导数 在几何上表示曲线 在点处的切线的斜率,即( 为倾角) 切线方程为切线方程为例10. 求等边双曲线 在点( ,2)处的切线的斜率,并写出在该点处的切线方程和法线方程.解 ,所求切线即法线的斜率分别为, .所求切线方程为 ,即 .所求切线方程为 ,即 .例11. 求曲线 的通过点(0,-4)的切线方程.解 设切点为 ( , ) ,则切线的斜率为于是所求切线方程可设为把(0,-4)代入上式,得解之得故所求切线方程为即四、函数的可导性与连续性的关系如果函数 在点 处可导,则它在点 处连续.证明 函数 在点 处可导,(其中 ) 函数 在点 处连续.注: 函数 在点 处连续,但在点 处不一定可导.如果函数 在点 处不连续,则在点 处一定不可导.连续但不可导的例子例12. 函数 在区间 内连续,但在点 处不可导.这是因为:在点 处有函数 在点 处导数为无穷大,即导数不存在.例13. 函数 在区间 内连续,但在点处不可导.内容小结1.导数的实质:增量之比的极限.2.3.导数的几何意义:切线的斜率.4.可导必连续,但连续不一定可导.5.已学求导公式特别地,特别地,5.可导性的判断方法:(1) 不连续,一定不可导;(2) 直接用导数定义;(3) 看左右导数是否存在且相等.
