北师大版八年级数学上册 4.1 函数 压轴练习 (无答案)
文档属性
| 名称 | 北师大版八年级数学上册 4.1 函数 压轴练习 (无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 279.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-23 00:00:00 | ||
图片预览



文档简介
4.1 函数(压轴练习)-北师大版八年级上册
一.选择题
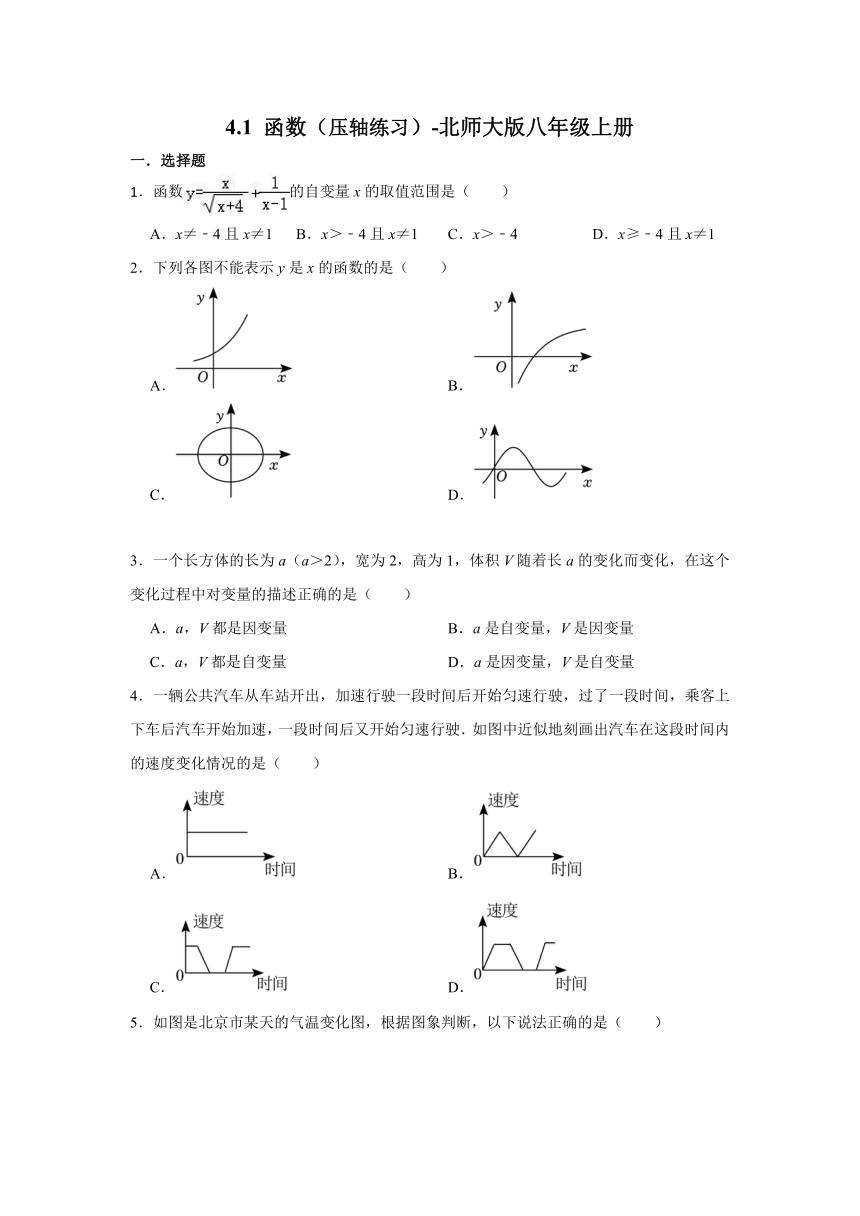
.函数的自变量x的取值范围是( )
A.x≠﹣4且x≠1 B.x>﹣4且x≠1 C.x>﹣4 D.x≥﹣4且x≠1
2.下列各图不能表示y是x的函数的是( )
A. B.
C. D.
3.一个长方体的长为a(a>2),宽为2,高为1,体积V随着长a的变化而变化,在这个变化过程中对变量的描述正确的是( )
A.a,V都是因变量 B.a是自变量,V是因变量
C.a,V都是自变量 D.a是因变量,V是自变量
4.一辆公共汽车从车站开出,加速行驶一段时间后开始匀速行驶,过了一段时间,乘客上下车后汽车开始加速,一段时间后又开始匀速行驶.如图中近似地刻画出汽车在这段时间内的速度变化情况的是( )
A. B.
C. D.
5.如图是北京市某天的气温变化图,根据图象判断,以下说法正确的是( )
A.当日最低气温是0℃
B.从早上6时开始气温逐渐升高,直到15时到达当日最高气温接近40℃
C.当日温度为10℃的时间点有两个
D.当日气温在20℃以下的时长超过12个小时
6.甲乙两同学从A地出发,骑自行车在同一条路上骑行到目的地B地,他们离出发
地的距离s(千米)和行驶时间t(时)之间的函数关系的图象,有下列说法:
①他们都骑行了18千米,但不是同时到达目的地;
②甲在中途停留了0.5小时;
③乙比甲晚出发了0.5小时,却早到了0.5小时;
④相遇后甲的速度大于乙的速度.
其中不符合图象描述的说法是( )
A.① B.② C.③ D.④
7.如图,在△ABC中,AD⊥BC,BC=7cm,点P是线段BC上一个动点,运动至点C停止,则△APC的面积S随点P的运动时间x之间的关系式为( )
A.S= 3x B.S=5(7﹣x)
C.S= D.S=
8.赵师傅到合肥某加油站加油,如图是所用的加油机上的数据显示牌,其中因变量是( )
A.金额 B.数量 C.单价 D.金额和数量
9.一条小船沿直线从A码头向B码头匀速前进,到达B码头后,停留一段时间,在整个过程中,这条小船与B码头的距离s(单位:m)(单位:min)之间的关系如图所示,则这条小船从A码头到B码头的速度和从B码头返回A码头的速度分别为( )
A.15m/min,25m/min B.25m/min,15m/min
C.25m/min,30m/min D.30m/min,25m/min
10.小明在游乐场坐过山车,在某一段60秒时间内过山车的高度h(米)与时间t(秒),则过山车距水平地面的最高高度为( )
A.98米 B.80米 C.53米 D.30米
二.填空题
11.某商店为减少某种商品的积压,采取降价销售的策略.商品原价为520元/件,随着不同幅度的降价,如下表所示:
降价/元 10 20 30 40 50 60 …
日销量/件 155 160 165 170 175 180 …
根据以上日销售量随降价幅度的变化情况,当售价为440元时,日销量为 件.
12.在一次实验中,小强把一根弹簧的上端固定,在其下端悬挂物体,写出弹簧长ycm与所挂重物xkg的关系式 .
所挂物重量x(kg) 0 1 2 3 4 5
弹簧长度y(cm) 20 22 24 26 28 30
13.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,它的高度h与n的函数关系是 .
14.下面的三个问题中都有两个变量:
①汽车从A地匀速行驶到B地,汽车的剩余路程y与行驶时间x;
②将水箱中的水匀速放出,直至放完,水箱中的剩余水量y与放水时间x;
③用长度一定的绳子围成一个矩形,矩形的面积y与一边长x.
其中,变量y与变量x之间的函数关系可以用如图所示的图象表示的是 (填序号).
15.自变量x与因变量y的关系如图,当x每增加1时,y增加 .
三.解答题
16.长方形的一边长是8,其邻边长为x,周长是y.
(1)写出x和y之间的关系式;
(2)当y=48时,x等于多少?
17.某公交车每月支出为4000元,每月的乘车人数x(人)与每月利润(利润=收入﹣支出)y(元)(每位乘客的公交票价是固定不变的).
x(人) … 500 1000 1500 2000 2500 3000
y(元) … ﹣3000 ﹣2000 ﹣1000 0 1000 2000
(1)在这个变化过程中,自变量是 ,因变量是 ;
(2)观察表中数据可知,每月乘客量至少达到 人时,该公交车才不会亏损;
(3)每位乘客的公交票价是 元;
(4)预测当每月乘车人数为5000人时,每月利润为 元.
18.某公交车每天的支出费用为600元,每天的乘车人数x(人)与每天利润(利润=票款收入﹣支出费用),如下表所示(每位乘客的乘车票价固定不变):
x(人) … 200 250 300 350 400 …
y(元) … ﹣200 ﹣100 0 100 200 …
根据表格中的数据,回答下列问题:
(1)观察表中数据可知,当乘客量达到 人以上时,该公交车才不会亏损;
(2)请写出公交车每天利润y(元)与每天乘车人数x(人)的关系式:y= ;
(3)当一天乘客人数为多少人时,利润是1000元?
19.由于惯性的作用.行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离“.为了测定某种型号小型载客汽车的刹车性能,(车速不超过140km/h).对这种型号的汽车进行了测试
刹车时车速v(km/h) 0 10 20 30 40 50 …
刹车距离s(m) 0 2.5 5 7.5 10 12.5 …
请回答下列问题,
(1)在这个变化过程中,自变量是 ,关于自变量的函数是 ;
(2)根据上表反映的规律写出该种型号汽车s与v之间的关系式: ;
(3)该型号汽车在高速公路上发生了一次交通事故.现场测得刹车距离为32m,推测刹车时车速是多少?并说明事故发生时,汽车是超速行驶还是正常行驶?(相关法规:《道路交通安全法》第七十八条:高速公路上行驶的小型载客汽车最高车速不得超过每小时120公里.)
20.如图是某市一天的气温变化图,在这一天中,气温随着时间变化而变化,回答下列问题.
(1)上午10时的气温是 ℃.
(2)在这一天中,(0时到24时均在内)气温在什么时候达到最高,最高温度是多少摄氏度?气温在什么时候达到最低
(3)如果某旅行团这天想去登山,登山的气温最好在18℃以上,请问该旅行团适宜登山的时间从几点开始
一.选择题
.函数的自变量x的取值范围是( )
A.x≠﹣4且x≠1 B.x>﹣4且x≠1 C.x>﹣4 D.x≥﹣4且x≠1
2.下列各图不能表示y是x的函数的是( )
A. B.
C. D.
3.一个长方体的长为a(a>2),宽为2,高为1,体积V随着长a的变化而变化,在这个变化过程中对变量的描述正确的是( )
A.a,V都是因变量 B.a是自变量,V是因变量
C.a,V都是自变量 D.a是因变量,V是自变量
4.一辆公共汽车从车站开出,加速行驶一段时间后开始匀速行驶,过了一段时间,乘客上下车后汽车开始加速,一段时间后又开始匀速行驶.如图中近似地刻画出汽车在这段时间内的速度变化情况的是( )
A. B.
C. D.
5.如图是北京市某天的气温变化图,根据图象判断,以下说法正确的是( )
A.当日最低气温是0℃
B.从早上6时开始气温逐渐升高,直到15时到达当日最高气温接近40℃
C.当日温度为10℃的时间点有两个
D.当日气温在20℃以下的时长超过12个小时
6.甲乙两同学从A地出发,骑自行车在同一条路上骑行到目的地B地,他们离出发
地的距离s(千米)和行驶时间t(时)之间的函数关系的图象,有下列说法:
①他们都骑行了18千米,但不是同时到达目的地;
②甲在中途停留了0.5小时;
③乙比甲晚出发了0.5小时,却早到了0.5小时;
④相遇后甲的速度大于乙的速度.
其中不符合图象描述的说法是( )
A.① B.② C.③ D.④
7.如图,在△ABC中,AD⊥BC,BC=7cm,点P是线段BC上一个动点,运动至点C停止,则△APC的面积S随点P的运动时间x之间的关系式为( )
A.S= 3x B.S=5(7﹣x)
C.S= D.S=
8.赵师傅到合肥某加油站加油,如图是所用的加油机上的数据显示牌,其中因变量是( )
A.金额 B.数量 C.单价 D.金额和数量
9.一条小船沿直线从A码头向B码头匀速前进,到达B码头后,停留一段时间,在整个过程中,这条小船与B码头的距离s(单位:m)(单位:min)之间的关系如图所示,则这条小船从A码头到B码头的速度和从B码头返回A码头的速度分别为( )
A.15m/min,25m/min B.25m/min,15m/min
C.25m/min,30m/min D.30m/min,25m/min
10.小明在游乐场坐过山车,在某一段60秒时间内过山车的高度h(米)与时间t(秒),则过山车距水平地面的最高高度为( )
A.98米 B.80米 C.53米 D.30米
二.填空题
11.某商店为减少某种商品的积压,采取降价销售的策略.商品原价为520元/件,随着不同幅度的降价,如下表所示:
降价/元 10 20 30 40 50 60 …
日销量/件 155 160 165 170 175 180 …
根据以上日销售量随降价幅度的变化情况,当售价为440元时,日销量为 件.
12.在一次实验中,小强把一根弹簧的上端固定,在其下端悬挂物体,写出弹簧长ycm与所挂重物xkg的关系式 .
所挂物重量x(kg) 0 1 2 3 4 5
弹簧长度y(cm) 20 22 24 26 28 30
13.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,它的高度h与n的函数关系是 .
14.下面的三个问题中都有两个变量:
①汽车从A地匀速行驶到B地,汽车的剩余路程y与行驶时间x;
②将水箱中的水匀速放出,直至放完,水箱中的剩余水量y与放水时间x;
③用长度一定的绳子围成一个矩形,矩形的面积y与一边长x.
其中,变量y与变量x之间的函数关系可以用如图所示的图象表示的是 (填序号).
15.自变量x与因变量y的关系如图,当x每增加1时,y增加 .
三.解答题
16.长方形的一边长是8,其邻边长为x,周长是y.
(1)写出x和y之间的关系式;
(2)当y=48时,x等于多少?
17.某公交车每月支出为4000元,每月的乘车人数x(人)与每月利润(利润=收入﹣支出)y(元)(每位乘客的公交票价是固定不变的).
x(人) … 500 1000 1500 2000 2500 3000
y(元) … ﹣3000 ﹣2000 ﹣1000 0 1000 2000
(1)在这个变化过程中,自变量是 ,因变量是 ;
(2)观察表中数据可知,每月乘客量至少达到 人时,该公交车才不会亏损;
(3)每位乘客的公交票价是 元;
(4)预测当每月乘车人数为5000人时,每月利润为 元.
18.某公交车每天的支出费用为600元,每天的乘车人数x(人)与每天利润(利润=票款收入﹣支出费用),如下表所示(每位乘客的乘车票价固定不变):
x(人) … 200 250 300 350 400 …
y(元) … ﹣200 ﹣100 0 100 200 …
根据表格中的数据,回答下列问题:
(1)观察表中数据可知,当乘客量达到 人以上时,该公交车才不会亏损;
(2)请写出公交车每天利润y(元)与每天乘车人数x(人)的关系式:y= ;
(3)当一天乘客人数为多少人时,利润是1000元?
19.由于惯性的作用.行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离“.为了测定某种型号小型载客汽车的刹车性能,(车速不超过140km/h).对这种型号的汽车进行了测试
刹车时车速v(km/h) 0 10 20 30 40 50 …
刹车距离s(m) 0 2.5 5 7.5 10 12.5 …
请回答下列问题,
(1)在这个变化过程中,自变量是 ,关于自变量的函数是 ;
(2)根据上表反映的规律写出该种型号汽车s与v之间的关系式: ;
(3)该型号汽车在高速公路上发生了一次交通事故.现场测得刹车距离为32m,推测刹车时车速是多少?并说明事故发生时,汽车是超速行驶还是正常行驶?(相关法规:《道路交通安全法》第七十八条:高速公路上行驶的小型载客汽车最高车速不得超过每小时120公里.)
20.如图是某市一天的气温变化图,在这一天中,气温随着时间变化而变化,回答下列问题.
(1)上午10时的气温是 ℃.
(2)在这一天中,(0时到24时均在内)气温在什么时候达到最高,最高温度是多少摄氏度?气温在什么时候达到最低
(3)如果某旅行团这天想去登山,登山的气温最好在18℃以上,请问该旅行团适宜登山的时间从几点开始
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
