苏科版九年级上册《11.5.1 认识机械效率》2023年同步练习卷(含解析)
文档属性
| 名称 | 苏科版九年级上册《11.5.1 认识机械效率》2023年同步练习卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 120.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-10-23 20:13:55 | ||
图片预览



文档简介
苏科版九年级上册《11.5.1 认识机械效率》2023年同步练习卷
一、选择题
1.做值日时,小阳将一桶水从一楼提到二楼。此过程中,关于做功的说法正确的是( )
A.对桶做的功是有用功
B.对水做的功是有用功
C.对水做的功是额外功
D.克服自身重力做的功是总功
2.机械甲的机械效率比机械乙的机械效率高,这表明( )
A.甲做的有用功比乙做的有用功多
B.甲做的总功比乙做的总功少
C.做相同的总功,甲做的有用功比乙做的有用功多
D.做相同的总功,甲做的有用功比乙做的有用功少
3.某同学不小心把水桶掉进井里,当他把桶从井里捞上来时,桶里带了一些水。下列有关有用功、额外功、总功的说法中正确的是( )
A.克服桶的重力做的功是总功
B.克服桶内水的重力做的功是有用功
C.克服桶的重力做的功是有用功
D.克服桶内水的重力做的功是总功
4.分别用杠杆、斜面和滑轮组将同一物体举到相同的高度,做的有用功是( )
A.一样多 B.斜面的多 C.滑轮组的多 D.杠杆的多
5.下列关于机械效率的说法错误的是( )
A.当总功一定时,有用功越多,机械效率越高
B.当有用功一定时,额外功越少,机械效率越高
C.当额外功一定时,有用功越多,机械效率越高
D.做有用功越多的机械,机械效率一定越高
6.下列关于功率和机械效率的说法中,正确的是( )
A.做功快的机械,功率一定大
B.功率大的机械,做功一定多
C.机械效率高的机械,功率一定大
D.做功多的机械,机械效率一定高
7.甲、乙两种机械的效率分别是70%和50%,则下列说法中正确的是( )
A.使用甲机械省力
B.使用甲机械省功
C.使用甲机械做功快
D.乙机械的额外功在总功中占的比例大
8.两台机械所做的总功之比是之2:1,它们的机械效率之比是3:4,则它们所做的有用功之比为( )
A.2:1 B.3:4 C.8:3 D.3:2
9.如图所示,斜面高2m、长4m,小明用平行于斜面的拉力F,将重400N的物体从斜面底端拉到顶端,已知拉力F=250N。对此过程,下列结果中正确的是( )
A.有用功为1000J B.总功为1600J
C.额外功为500J D.机械效率为80%
二、填空题
10.升旗过程中,克服旗的重力做的功是 ,克服绳子重力做的功是 ;克服摩擦力做的功是 。(填“有用功”“额外功”或“总功”)
11.某滑轮组的机械效率为80%表示的含义是 ,当它完成1000J的总功时,所做的有用功为 J,若克服动滑轮的重力所做的功是150J,则克服摩擦和绳重所做的功是 J
12.用如图甲的滑轮组提升重200N的物体,已知拉力F为80N,不计绳重和摩擦,物体和绳子自由端的运动情况如图乙所示,反映绳子自由端运动的图线是 (选填“A”或“B”),动滑轮重为 N,3s内对物体做的有用功为 J。
13.重为5N的钩码挂在A点时,人的拉力F为4N,钩码上升0.3m时,动力作用点C上升0.5m,此时机械效率为 。在这个过程中,克服摩擦和杠杆自身重力所做的功是 J。
三、实验探究题
14.在“探究滑轮”的实验中,小明所在实验小组,进行了如下实验。
(1)用弹簧测力计沿竖直方向 拉一个动滑轮,使挂在它下面的钩码缓缓上升,测量拉力F、绳端移动的距离s,钩码所受重力G及其上升的高度h。
实验序号 手拉绳子的力F/N 手移动的距离s/cm 钩码的重力G/N 钩码上升的高度h/cm
1 0.60 10 1.00 5
2 0.85 10 1.50 5
3 1.10 10 2.00 5
(2)为了多测几组数据,我们可以改变 ,也可以改变钩码上升高度,重复上述步骤。
(3)将实验数据填入表格中。
①该实验的目的是探究比较 与动滑轮拉钩码所做的功是否相等。
②根据实验目的分析实验数据可知,使用动滑轮 (能/不能)省功。
四、计算题
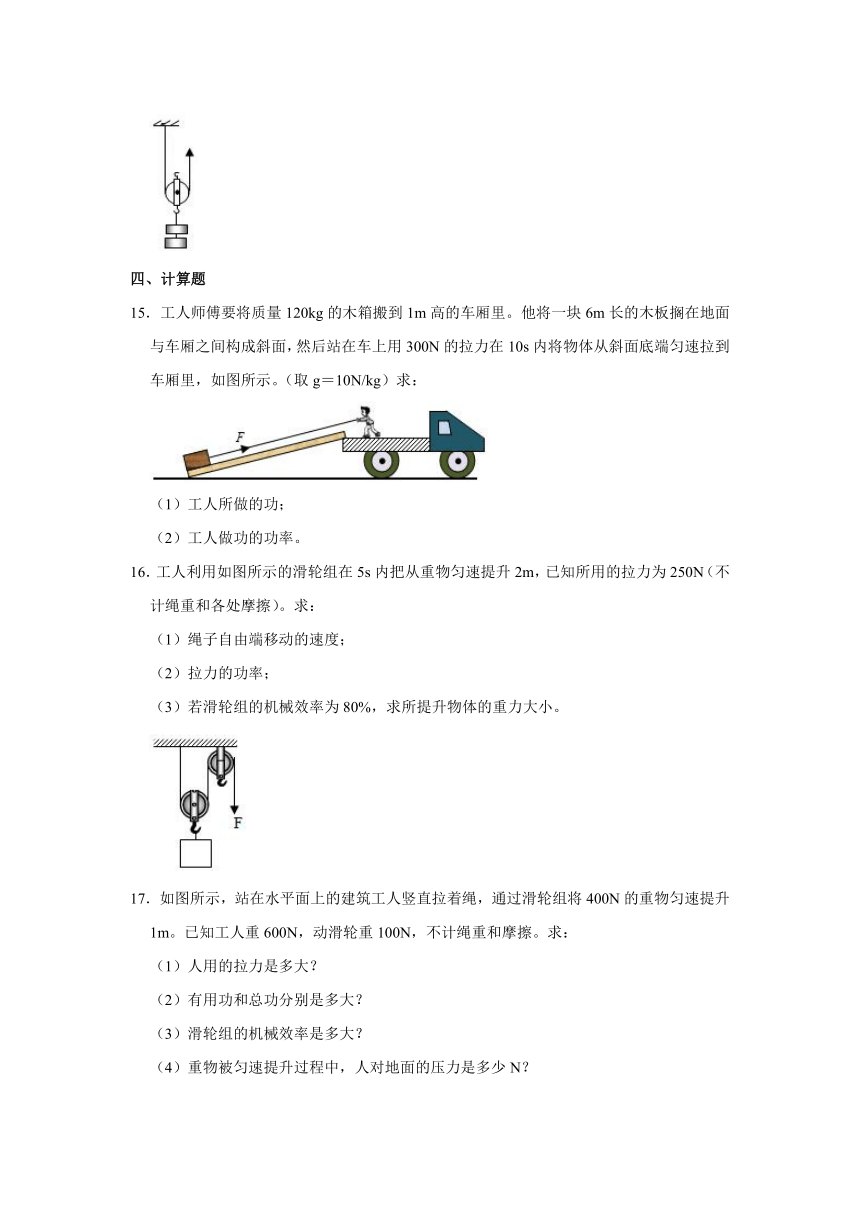
15.工人师傅要将质量120kg的木箱搬到1m高的车厢里。他将一块6m长的木板搁在地面与车厢之间构成斜面,然后站在车上用300N的拉力在10s内将物体从斜面底端匀速拉到车厢里,如图所示。(取g=10N/kg)求:
(1)工人所做的功;
(2)工人做功的功率。
16.工人利用如图所示的滑轮组在5s内把从重物匀速提升2m,已知所用的拉力为250N(不计绳重和各处摩擦)。求:
(1)绳子自由端移动的速度;
(2)拉力的功率;
(3)若滑轮组的机械效率为80%,求所提升物体的重力大小。
17.如图所示,站在水平面上的建筑工人竖直拉着绳,通过滑轮组将400N的重物匀速提升1m。已知工人重600N,动滑轮重100N,不计绳重和摩擦。求:
(1)人用的拉力是多大?
(2)有用功和总功分别是多大?
(3)滑轮组的机械效率是多大?
(4)重物被匀速提升过程中,人对地面的压力是多少N?
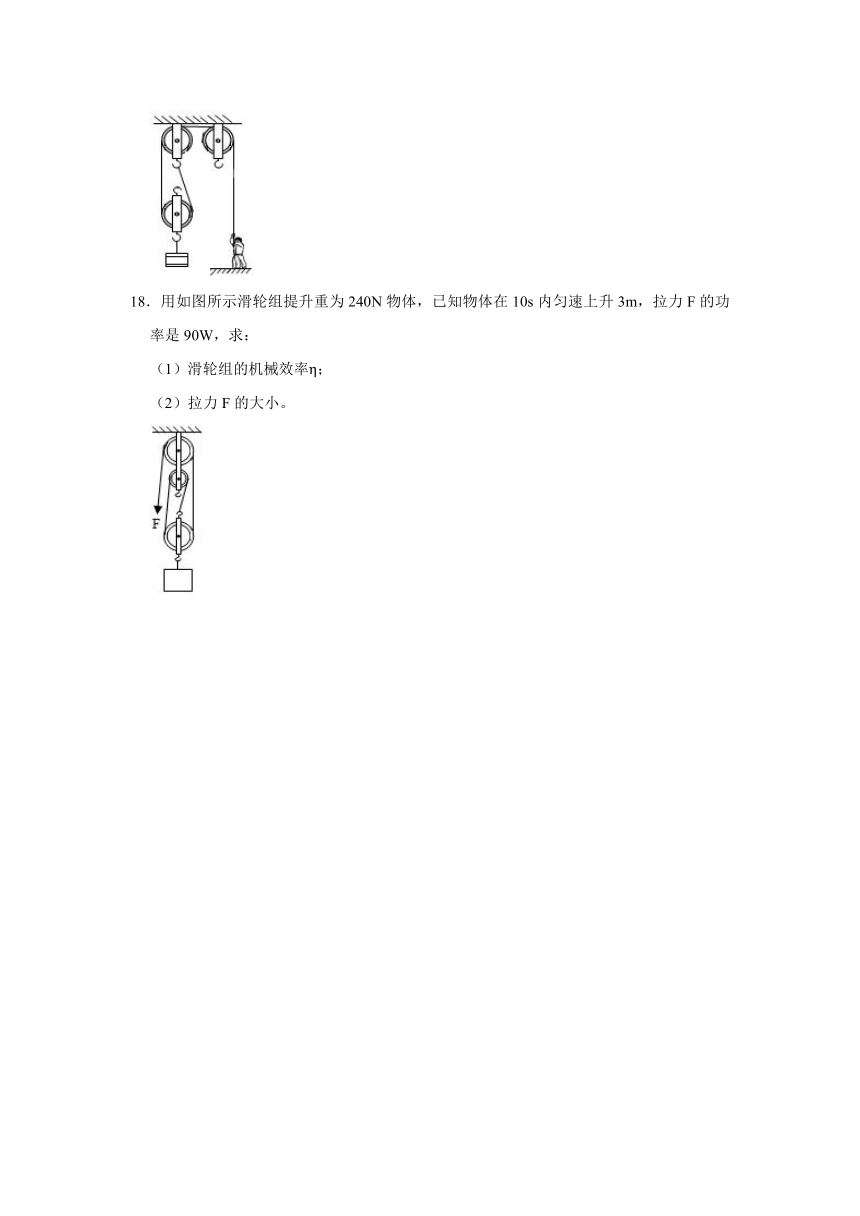
18.用如图所示滑轮组提升重为240N物体,已知物体在10s内匀速上升3m,拉力F的功率是90W,求:
(1)滑轮组的机械效率η;
(2)拉力F的大小。
苏科版九年级上册《11.5.1 认识机械效率》2023年同步练习卷
参考答案与试题解析
一、选择题
1.【解答】解:小阳目的是提水,对水做的功为有用功,故B正确、C错;
对桶做的功为额外功,故A错;
小阳把水、桶、自身提升做的功为总功,故D错。
故选:B。
2.【解答】解:根据机械效率定义,知:
在没有确定总功或有用功两个量中一个相等时,没法比较另一个的大小,故A、B选项不对;
而C、D选项总功相等,甲的机械效率高,甲做的有用功多;
故选:C。
3.【解答】解:
由题意可知,该同学的目的是把桶从井里捞上来,所以克服桶的重力做的功是有用功;因桶里带了一些水,但又不得不对水做功,即克服桶内水的重力做的功是额外功;而克服水和桶的总重力做的功是总功,故C正确,ABD错误。
故选:C。
4.【解答】解:用杠杆、斜面和滑轮组将同一物体举到相同的高度,根据公式W=Gh可知,做的有用功相等。
故选:A。
5.【解答】解:A、由公式η=知,在总功一定时,有用功越多,机械效率越高,故A正确;
B、由公式η==知,在有用功一定时,额外功越少,机械效率越高,故B正确;
C、由公式η==知,在额外功一定时,有用功越多,机械效率越高,故C正确;
D、由公式η=知,有用功较多,总功不确定,机械效率不能确定,故D错误。
故选:D。
6.【解答】解:
A、说法正确,因为功率就是描述物体做功快慢的物理量。做功快,功率一定大。
B、说法错误,物体做功多少与功率和时间都有关系。功率大,时间不确定,功率不能确定。
C、说法错误,由于机械效率是有用功与总功的比值。机械效率高,功率不一定大;
D、由于机械效率是有用功与总功的比值,做功多,机械效率不一定高。
故选:A。
7.【解答】解:A、机械效率高是指做的功中有用功占的比例高,与是否省力没有关系。故此项不符合题意。
B、使用任何机械都不省功。故此项不符合题意。
C、功率是表示做功的快慢,而功率与机械效率没有必然的联系。故此项不符合题意。
D、乙的机械效率较低,说明有用功占总功的比例小,相应的,额外功占总功的比例就比较大。此项符合题意。
故选:D。
8.【解答】解:由η=可得,W有1:W有2=η1W总1:η2W总2=3×2:4×1=3:2。
故选:D。
9.【解答】解:
A、小明对物体做的有用功:W有用=Gh=400N×2m=800J,故A错误;
B、拉力F做的总功:W总=Fs=250N×4m=1000J,故B错误;
C、额外功:W额=W总﹣W有用=1000J﹣800J=200J,故C错误;
D、斜面的机械效率:
η==×100%=80%,故D正确。
故选:D。
二、填空题
10.【解答】解:我们的目的是把旗提升到一定高度,所以升旗过程中,克服旗的重力做的功是有用功;
克服绳子重力做的功和克服摩擦力做的功是没有用的但又不得不做的功,即额外功。
故答案为:有用功;额外功;额外功。
11.【解答】解:
机械效率是指有用功占总功的百分比,某滑轮组的机械效率为80%,其含义是有用功占总功的80%。
由此可知,当它完成1000J的总功时,所做的有用功为W有用=η×W总=80%×1000J=800J,
额外功:W额总=W总﹣W有=1000J﹣800J=200J,
已知克服动滑轮的重力所做的功是150J,则克服摩擦和绳重所做的功W额=200J﹣150J=50J。
故答案为:用该滑轮组做功时有用功占总功的80%;800;50。
12.【解答】解:(1)由图甲可知,n=3,则拉力端移动距离s=3h,所以图乙中上面的倾斜直线A是绳子自由端运动的s﹣t图像,而下面的倾斜直线B是物体运动的s﹣t图像;
(2)不计绳重和摩擦,拉力F=(G+G动),则动滑轮重力:
G动=3F﹣G=3×80N﹣200N=40N;
(3)由图乙可知,t=3s时,物体运动的高度h=1.5m,
对物体做的有用功:W有用=Gh=200N×1.5m=300J。
故答案为:A;40;300。
13.【解答】解:(1)拉力作的有用功:
W有用=Gh=5N×0.3m=1.5J,
拉力做的总功:
W总=Fs=4N×0.5m=2J,
杠杆的机械效率:
η===75%;
(2)克服摩擦和杠杆自身重力所做的额外功:
W额=W总﹣W有用=2J﹣1.5J=0.5J。
故答案为:75%;0.5。
三、实验探究题
14.【解答】解:(1)用弹簧测力计沿竖直方向匀速拉一个动滑轮,此时系统处于平衡状态,测力计示数等于拉力大小,使挂在它下面钩码缓缓上升,测量拉力F。
(2)为了多测几组数据,我们可以改变提升物体的重力,即改变钩码的个数,也可以改变钩码上升高度,重复上述步骤。
(3)①由表中数据知,根据W=Fs,可求出拉力做的功,故该实验的目的是探究比较动力做的功与动滑轮拉钩码所做的功是否相等。
②根据实验目的分析实验数据可知,动力做的功:W1=F1s1=0.6N×0.1m=0.06J,
动滑轮拉钩码所做的功:W1′=G′1h′1=1N×0.05m=0.05J,
所以W1>W1′,同理第2、3次动力做的功也大于动滑轮拉钩码所做的功,
故使用动滑轮不能省功。
故答案为:(1)匀速;(2)钩码的个数;(3)①动力做的功;②不能。
四、计算题
15.【解答】解:(1)工人所做的功W=Fs=300N×6m=1800J。
(2)工人做功的功率P==180W。
答:(1)工人所做的功是1800J;
(2)工人做功的功率是180W。
16.【解答】解:
(1)由图知n=2,绳子自由端移动的距离s=2h=2×2m=4m,
绳子自由端移动的速度:
v===0.8m/s;
(2)拉力做的总功:
W总=Fs=250N×4m=1000J,
拉力的功率:
P===200W;
(3)根据η=×100%得有用功:
W有用=η×W总=80%×1000J=800J;
由W有用=Gh可得物体的重力:
G===400N。
答:(1)绳子自由端移动的速度为0.8m/s;
(2)拉力的功率为200W;
(3)若滑轮组的机械效率为80%,所提升物体的重力大小为400N。
17.【解答】解:(1)由图可知,滑轮组绳子的有效股数n=2,
不计绳重和摩擦,人用的拉力:F=(G+G动)=×(400N+100N)=250N;
(2)拉力所做的有用功:W有=Gh=400N×1m=400J,
绳子自由端移动的距离:s=nh=2×1m=2m,
拉力所做的总功:W总=Fs=250N×2m=500J;
(3)滑轮组的机械效率:η=×100%=×100%=80%;
(4)重物被匀速提升过程中,人对地面的压力:F压=G人﹣F=600N﹣250N=350N。
答:(1)人用的拉力是250N;
(2)有用功和总功分别是500J;
(3)滑轮组的机械效率是80%;
(4)重物被匀速提升过程中,人对地面的压力是350N。
18.【解答】解:(1)提升物体做的有用功:W有=Gh=240N×3m=720J;
由P=可得,拉力所做的总功:W总=Pt=90W×10s=900J,
滑轮组的机械效率η=×100%=×100%=80%;
(2)由图可知,滑轮组绳子的有效股数n=3,
则绳端移动的距离s=nh=3×3m=9m,
由W=Fs可得,拉力F===100N。
答:(1)滑轮组的机械效率为80%;
(2)拉力F的大小为100N。
一、选择题
1.做值日时,小阳将一桶水从一楼提到二楼。此过程中,关于做功的说法正确的是( )
A.对桶做的功是有用功
B.对水做的功是有用功
C.对水做的功是额外功
D.克服自身重力做的功是总功
2.机械甲的机械效率比机械乙的机械效率高,这表明( )
A.甲做的有用功比乙做的有用功多
B.甲做的总功比乙做的总功少
C.做相同的总功,甲做的有用功比乙做的有用功多
D.做相同的总功,甲做的有用功比乙做的有用功少
3.某同学不小心把水桶掉进井里,当他把桶从井里捞上来时,桶里带了一些水。下列有关有用功、额外功、总功的说法中正确的是( )
A.克服桶的重力做的功是总功
B.克服桶内水的重力做的功是有用功
C.克服桶的重力做的功是有用功
D.克服桶内水的重力做的功是总功
4.分别用杠杆、斜面和滑轮组将同一物体举到相同的高度,做的有用功是( )
A.一样多 B.斜面的多 C.滑轮组的多 D.杠杆的多
5.下列关于机械效率的说法错误的是( )
A.当总功一定时,有用功越多,机械效率越高
B.当有用功一定时,额外功越少,机械效率越高
C.当额外功一定时,有用功越多,机械效率越高
D.做有用功越多的机械,机械效率一定越高
6.下列关于功率和机械效率的说法中,正确的是( )
A.做功快的机械,功率一定大
B.功率大的机械,做功一定多
C.机械效率高的机械,功率一定大
D.做功多的机械,机械效率一定高
7.甲、乙两种机械的效率分别是70%和50%,则下列说法中正确的是( )
A.使用甲机械省力
B.使用甲机械省功
C.使用甲机械做功快
D.乙机械的额外功在总功中占的比例大
8.两台机械所做的总功之比是之2:1,它们的机械效率之比是3:4,则它们所做的有用功之比为( )
A.2:1 B.3:4 C.8:3 D.3:2
9.如图所示,斜面高2m、长4m,小明用平行于斜面的拉力F,将重400N的物体从斜面底端拉到顶端,已知拉力F=250N。对此过程,下列结果中正确的是( )
A.有用功为1000J B.总功为1600J
C.额外功为500J D.机械效率为80%
二、填空题
10.升旗过程中,克服旗的重力做的功是 ,克服绳子重力做的功是 ;克服摩擦力做的功是 。(填“有用功”“额外功”或“总功”)
11.某滑轮组的机械效率为80%表示的含义是 ,当它完成1000J的总功时,所做的有用功为 J,若克服动滑轮的重力所做的功是150J,则克服摩擦和绳重所做的功是 J
12.用如图甲的滑轮组提升重200N的物体,已知拉力F为80N,不计绳重和摩擦,物体和绳子自由端的运动情况如图乙所示,反映绳子自由端运动的图线是 (选填“A”或“B”),动滑轮重为 N,3s内对物体做的有用功为 J。
13.重为5N的钩码挂在A点时,人的拉力F为4N,钩码上升0.3m时,动力作用点C上升0.5m,此时机械效率为 。在这个过程中,克服摩擦和杠杆自身重力所做的功是 J。
三、实验探究题
14.在“探究滑轮”的实验中,小明所在实验小组,进行了如下实验。
(1)用弹簧测力计沿竖直方向 拉一个动滑轮,使挂在它下面的钩码缓缓上升,测量拉力F、绳端移动的距离s,钩码所受重力G及其上升的高度h。
实验序号 手拉绳子的力F/N 手移动的距离s/cm 钩码的重力G/N 钩码上升的高度h/cm
1 0.60 10 1.00 5
2 0.85 10 1.50 5
3 1.10 10 2.00 5
(2)为了多测几组数据,我们可以改变 ,也可以改变钩码上升高度,重复上述步骤。
(3)将实验数据填入表格中。
①该实验的目的是探究比较 与动滑轮拉钩码所做的功是否相等。
②根据实验目的分析实验数据可知,使用动滑轮 (能/不能)省功。
四、计算题
15.工人师傅要将质量120kg的木箱搬到1m高的车厢里。他将一块6m长的木板搁在地面与车厢之间构成斜面,然后站在车上用300N的拉力在10s内将物体从斜面底端匀速拉到车厢里,如图所示。(取g=10N/kg)求:
(1)工人所做的功;
(2)工人做功的功率。
16.工人利用如图所示的滑轮组在5s内把从重物匀速提升2m,已知所用的拉力为250N(不计绳重和各处摩擦)。求:
(1)绳子自由端移动的速度;
(2)拉力的功率;
(3)若滑轮组的机械效率为80%,求所提升物体的重力大小。
17.如图所示,站在水平面上的建筑工人竖直拉着绳,通过滑轮组将400N的重物匀速提升1m。已知工人重600N,动滑轮重100N,不计绳重和摩擦。求:
(1)人用的拉力是多大?
(2)有用功和总功分别是多大?
(3)滑轮组的机械效率是多大?
(4)重物被匀速提升过程中,人对地面的压力是多少N?
18.用如图所示滑轮组提升重为240N物体,已知物体在10s内匀速上升3m,拉力F的功率是90W,求:
(1)滑轮组的机械效率η;
(2)拉力F的大小。
苏科版九年级上册《11.5.1 认识机械效率》2023年同步练习卷
参考答案与试题解析
一、选择题
1.【解答】解:小阳目的是提水,对水做的功为有用功,故B正确、C错;
对桶做的功为额外功,故A错;
小阳把水、桶、自身提升做的功为总功,故D错。
故选:B。
2.【解答】解:根据机械效率定义,知:
在没有确定总功或有用功两个量中一个相等时,没法比较另一个的大小,故A、B选项不对;
而C、D选项总功相等,甲的机械效率高,甲做的有用功多;
故选:C。
3.【解答】解:
由题意可知,该同学的目的是把桶从井里捞上来,所以克服桶的重力做的功是有用功;因桶里带了一些水,但又不得不对水做功,即克服桶内水的重力做的功是额外功;而克服水和桶的总重力做的功是总功,故C正确,ABD错误。
故选:C。
4.【解答】解:用杠杆、斜面和滑轮组将同一物体举到相同的高度,根据公式W=Gh可知,做的有用功相等。
故选:A。
5.【解答】解:A、由公式η=知,在总功一定时,有用功越多,机械效率越高,故A正确;
B、由公式η==知,在有用功一定时,额外功越少,机械效率越高,故B正确;
C、由公式η==知,在额外功一定时,有用功越多,机械效率越高,故C正确;
D、由公式η=知,有用功较多,总功不确定,机械效率不能确定,故D错误。
故选:D。
6.【解答】解:
A、说法正确,因为功率就是描述物体做功快慢的物理量。做功快,功率一定大。
B、说法错误,物体做功多少与功率和时间都有关系。功率大,时间不确定,功率不能确定。
C、说法错误,由于机械效率是有用功与总功的比值。机械效率高,功率不一定大;
D、由于机械效率是有用功与总功的比值,做功多,机械效率不一定高。
故选:A。
7.【解答】解:A、机械效率高是指做的功中有用功占的比例高,与是否省力没有关系。故此项不符合题意。
B、使用任何机械都不省功。故此项不符合题意。
C、功率是表示做功的快慢,而功率与机械效率没有必然的联系。故此项不符合题意。
D、乙的机械效率较低,说明有用功占总功的比例小,相应的,额外功占总功的比例就比较大。此项符合题意。
故选:D。
8.【解答】解:由η=可得,W有1:W有2=η1W总1:η2W总2=3×2:4×1=3:2。
故选:D。
9.【解答】解:
A、小明对物体做的有用功:W有用=Gh=400N×2m=800J,故A错误;
B、拉力F做的总功:W总=Fs=250N×4m=1000J,故B错误;
C、额外功:W额=W总﹣W有用=1000J﹣800J=200J,故C错误;
D、斜面的机械效率:
η==×100%=80%,故D正确。
故选:D。
二、填空题
10.【解答】解:我们的目的是把旗提升到一定高度,所以升旗过程中,克服旗的重力做的功是有用功;
克服绳子重力做的功和克服摩擦力做的功是没有用的但又不得不做的功,即额外功。
故答案为:有用功;额外功;额外功。
11.【解答】解:
机械效率是指有用功占总功的百分比,某滑轮组的机械效率为80%,其含义是有用功占总功的80%。
由此可知,当它完成1000J的总功时,所做的有用功为W有用=η×W总=80%×1000J=800J,
额外功:W额总=W总﹣W有=1000J﹣800J=200J,
已知克服动滑轮的重力所做的功是150J,则克服摩擦和绳重所做的功W额=200J﹣150J=50J。
故答案为:用该滑轮组做功时有用功占总功的80%;800;50。
12.【解答】解:(1)由图甲可知,n=3,则拉力端移动距离s=3h,所以图乙中上面的倾斜直线A是绳子自由端运动的s﹣t图像,而下面的倾斜直线B是物体运动的s﹣t图像;
(2)不计绳重和摩擦,拉力F=(G+G动),则动滑轮重力:
G动=3F﹣G=3×80N﹣200N=40N;
(3)由图乙可知,t=3s时,物体运动的高度h=1.5m,
对物体做的有用功:W有用=Gh=200N×1.5m=300J。
故答案为:A;40;300。
13.【解答】解:(1)拉力作的有用功:
W有用=Gh=5N×0.3m=1.5J,
拉力做的总功:
W总=Fs=4N×0.5m=2J,
杠杆的机械效率:
η===75%;
(2)克服摩擦和杠杆自身重力所做的额外功:
W额=W总﹣W有用=2J﹣1.5J=0.5J。
故答案为:75%;0.5。
三、实验探究题
14.【解答】解:(1)用弹簧测力计沿竖直方向匀速拉一个动滑轮,此时系统处于平衡状态,测力计示数等于拉力大小,使挂在它下面钩码缓缓上升,测量拉力F。
(2)为了多测几组数据,我们可以改变提升物体的重力,即改变钩码的个数,也可以改变钩码上升高度,重复上述步骤。
(3)①由表中数据知,根据W=Fs,可求出拉力做的功,故该实验的目的是探究比较动力做的功与动滑轮拉钩码所做的功是否相等。
②根据实验目的分析实验数据可知,动力做的功:W1=F1s1=0.6N×0.1m=0.06J,
动滑轮拉钩码所做的功:W1′=G′1h′1=1N×0.05m=0.05J,
所以W1>W1′,同理第2、3次动力做的功也大于动滑轮拉钩码所做的功,
故使用动滑轮不能省功。
故答案为:(1)匀速;(2)钩码的个数;(3)①动力做的功;②不能。
四、计算题
15.【解答】解:(1)工人所做的功W=Fs=300N×6m=1800J。
(2)工人做功的功率P==180W。
答:(1)工人所做的功是1800J;
(2)工人做功的功率是180W。
16.【解答】解:
(1)由图知n=2,绳子自由端移动的距离s=2h=2×2m=4m,
绳子自由端移动的速度:
v===0.8m/s;
(2)拉力做的总功:
W总=Fs=250N×4m=1000J,
拉力的功率:
P===200W;
(3)根据η=×100%得有用功:
W有用=η×W总=80%×1000J=800J;
由W有用=Gh可得物体的重力:
G===400N。
答:(1)绳子自由端移动的速度为0.8m/s;
(2)拉力的功率为200W;
(3)若滑轮组的机械效率为80%,所提升物体的重力大小为400N。
17.【解答】解:(1)由图可知,滑轮组绳子的有效股数n=2,
不计绳重和摩擦,人用的拉力:F=(G+G动)=×(400N+100N)=250N;
(2)拉力所做的有用功:W有=Gh=400N×1m=400J,
绳子自由端移动的距离:s=nh=2×1m=2m,
拉力所做的总功:W总=Fs=250N×2m=500J;
(3)滑轮组的机械效率:η=×100%=×100%=80%;
(4)重物被匀速提升过程中,人对地面的压力:F压=G人﹣F=600N﹣250N=350N。
答:(1)人用的拉力是250N;
(2)有用功和总功分别是500J;
(3)滑轮组的机械效率是80%;
(4)重物被匀速提升过程中,人对地面的压力是350N。
18.【解答】解:(1)提升物体做的有用功:W有=Gh=240N×3m=720J;
由P=可得,拉力所做的总功:W总=Pt=90W×10s=900J,
滑轮组的机械效率η=×100%=×100%=80%;
(2)由图可知,滑轮组绳子的有效股数n=3,
则绳端移动的距离s=nh=3×3m=9m,
由W=Fs可得,拉力F===100N。
答:(1)滑轮组的机械效率为80%;
(2)拉力F的大小为100N。
同课章节目录
- 第十一章 简单机械和功
- 1 杠杆
- 2 滑轮
- 3 功
- 4 功率
- 5 机械效率
- 第十二章 机械能和内能
- 1 动能 势能 机械能
- 2 内能 热传递
- 3 物质的比热容
- 4 机械能和内能的相互转化
- 第十三章 电路初探
- 1 初识家用电器和电路
- 2 电路连接的基本方式
- 3 电流和电流表的使用
- 4 电压和电压表的使用
- 第十四章 欧姆定律
- 1 电阻
- 2 变阻器
- 3 欧姆定律
- 4 欧姆定律的应用
- 第十五章 电功和电热
- 电能表与电功
- 电功率
- 电热器 电流的热效应
- 家庭电路与安全用电
- 第十六章 电磁转换
- 磁体与磁场
- 电流的磁场
- 磁场对电流的作用 电动机
- 安装直流电动机模型
- 电磁感应 发电机
- 第十七章 电磁波与现代通信
- 信息与信息传播
- 电磁波及其传播
- 现代通信 走进信息时代
- 第十八章 能源与可持续发展
- 能源利用与社会发展
- 核能
- 太阳能
- 能量转化的基本规律
- 能源与可持续发展
