苏科版九年级上册《12.2 内能 热传递 12.3 物质的比热容》2023年同步练习卷(含解析)
文档属性
| 名称 | 苏科版九年级上册《12.2 内能 热传递 12.3 物质的比热容》2023年同步练习卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 243.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-10-23 20:16:45 | ||
图片预览


文档简介
苏科版九年级上册《12.2 内能 热传递 物质的比热容》2023年同步练习卷
一、选择题
1.用稳定的热源给一个物体均匀加热,设物体吸收的热量与加热时间成正比,得到其温度随时间变化的曲线如图所示,那么它在固态时的比热与液态时的比热之比是( )
A.1:2 B.2:1 C.1:4 D.4:1
2.将一杯热水倒入盛有冷水的容器中,冷水的温度升高了10℃,再向容器内倒入一杯相同质量和温度的热水,容器中的水温又升高了6℃。如果继续向容器中倒入5杯同样的热水,则容器中的水温会升高(不计热量损失)( )
A.14℃ B.12℃ C.9℃ D.4℃
3.甲、乙两物体吸收相等热量后,甲物体的温度变化量大。如甲物体的比热容为c甲,质量为m甲,乙物体比热容为c乙,质量是m乙,则下列说法中,一定错误的是( )
A.若m甲=m乙,则c甲<c乙 B.若c甲=c乙,则m甲<m乙
C.若m甲>m乙,则c甲>c乙 D.若c甲<c乙,则m甲<m乙
4.有两个温度和质量都相同的金属球,先把甲球放入盛有热水的杯中,热平衡后水温降低了Δt.把甲球取出,再将乙球放入杯中,热平衡后水温又降低了Δt,则甲球比热c甲和乙球比热c乙大小的关系是( )
A.c甲>c乙 B.c甲<c乙
C.c甲=c乙 D.以上三种情况都有可能
5.冷水的质量为m,温度为t1,吸收一定热量后,温度升高到t;另有质量为2m的热水,如果先放出同样热量后温度也降到t,那么热水原来的温度应是( )
A. B. C. D.
6.如图是用相同的加热装置对a、b、c(已知质量关系为mb=mc)三种物质加热至沸腾时,它们的温度随时间变化的图象。下列对图象的分析正确的是( )
A.b的比热容大于c的比热容
B.t1﹣t2时间内物质a的温度不变,内能不变
C.温度从T1升高到T2时,a物质吸收的热量比b多
D.如果a、b是同种物质,b的质量大于a的质量
7.网上曾热销一时的“55度杯”,称“能很快将开水变成适饮的温水,而后又能将凉水变成适饮的温水”。为破解此中秘密,某同学设计了如图乙模型。设此杯内胆中被封存着300g水,室温20℃;现向杯中倒入200g、100℃开水,摇一摇,杯内水温迅速降至t1,饮用后迅速将200g室温矿泉水倒入该杯,摇一摇,矿泉水的温度可升至t2,若忽略内胆及空间的热能消耗,则t1,t2分别大约为( )
A.50℃50℃ B.52℃39.2℃ C.40℃60℃ D.55℃55℃
8.质量相等的甲、乙两金属块,其材质不同。将它们放入沸水中,一段时间后温度均达到100℃,然后将它们按不同的方式投入一杯冷水中,使冷水升温。第一种方式:先从沸水中取出甲,将其投入冷水,当达到热平衡后将甲从杯中取出,测得水温升高10℃;然后将乙从沸水中取出投入这杯水中,再次达到热平衡,测得水温又升高了10℃.第二种方式:从沸水中取出甲、乙投入冷水,使之达到热平衡。则在第二种方式下,这杯冷水温度的变化是( )
A.升高不足20℃ B.升高超过20℃
C.恰好升高了20℃ D.条件不足,无法判断
二、多选题
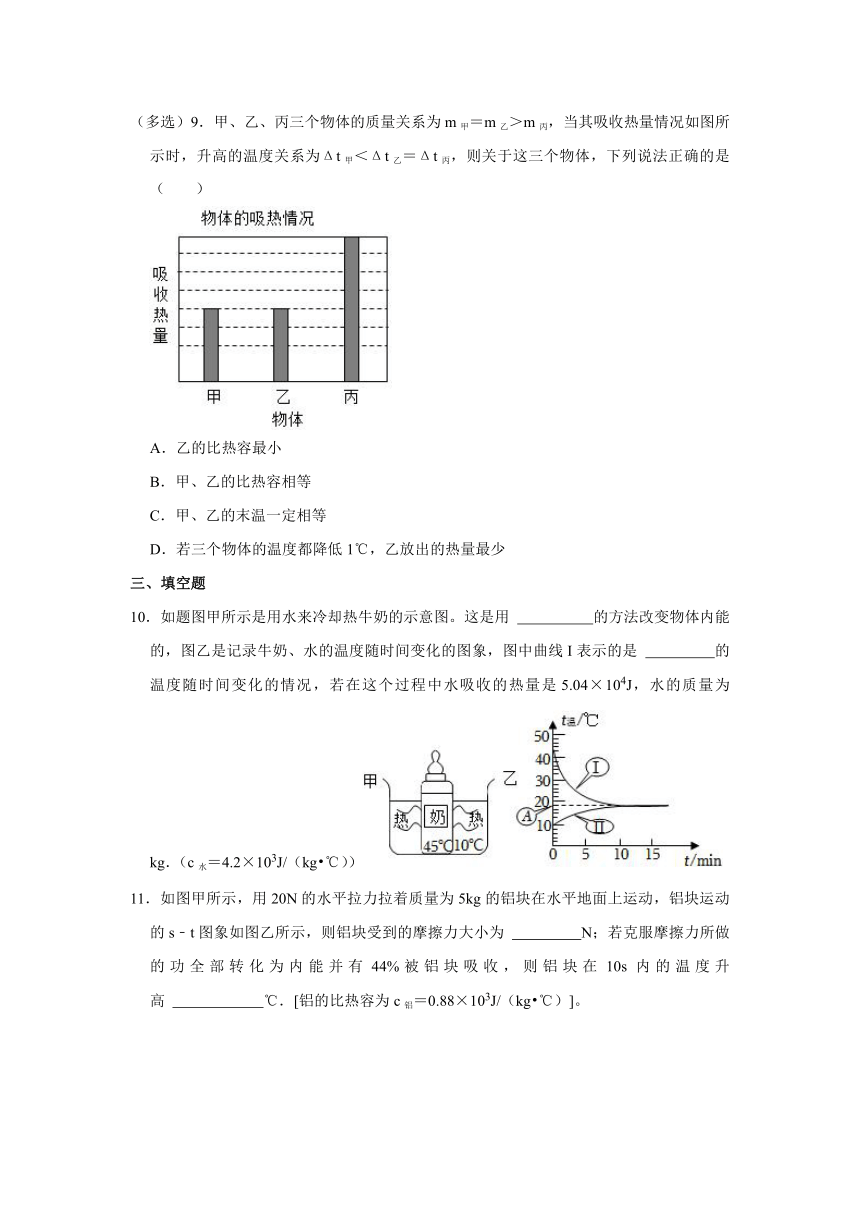
(多选)9.甲、乙、丙三个物体的质量关系为m甲=m乙>m丙,当其吸收热量情况如图所示时,升高的温度关系为Δt甲<Δt乙=Δt丙,则关于这三个物体,下列说法正确的是( )
A.乙的比热容最小
B.甲、乙的比热容相等
C.甲、乙的末温一定相等
D.若三个物体的温度都降低1℃,乙放出的热量最少
三、填空题
10.如题图甲所示是用水来冷却热牛奶的示意图。这是用 的方法改变物体内能的,图乙是记录牛奶、水的温度随时间变化的图象,图中曲线I表示的是 的温度随时间变化的情况,若在这个过程中水吸收的热量是5.04×104J,水的质量为 kg.(c水=4.2×103J/(kg ℃))
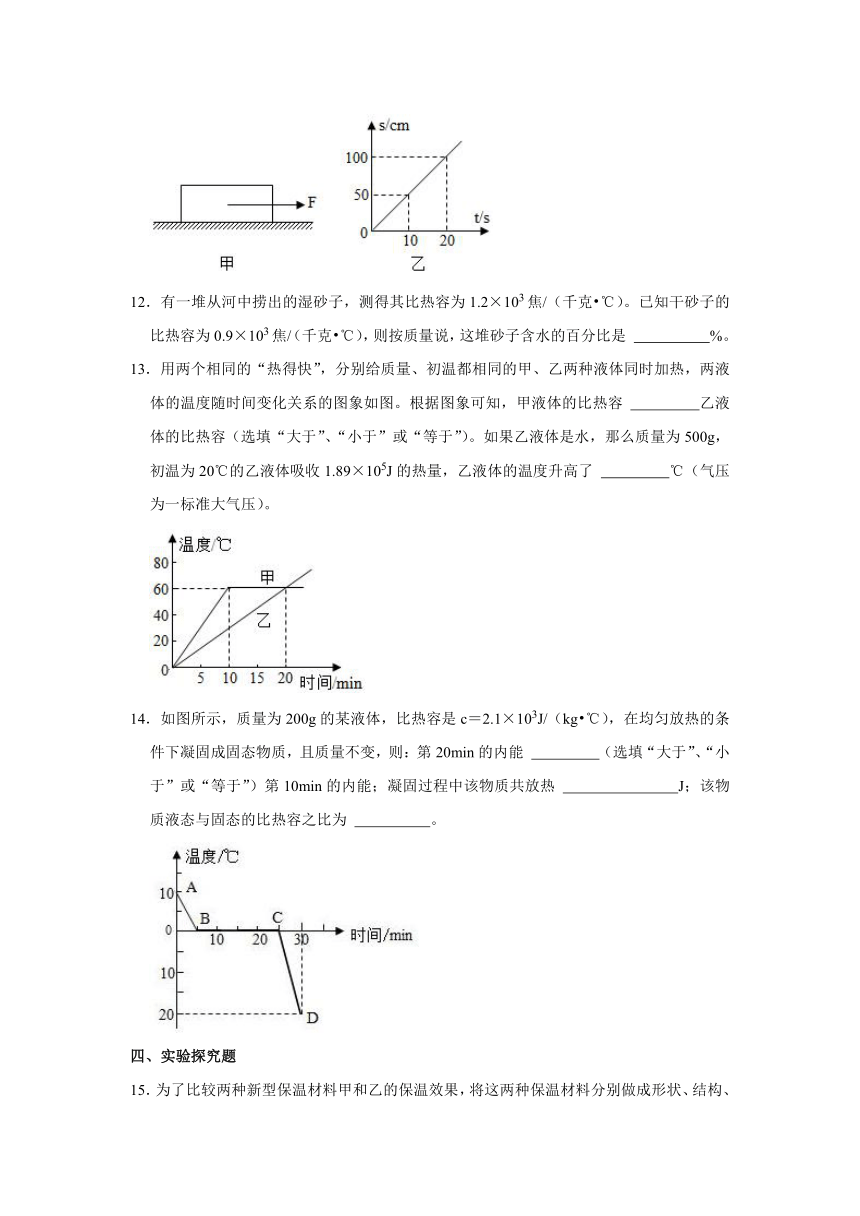
11.如图甲所示,用20N的水平拉力拉着质量为5kg的铝块在水平地面上运动,铝块运动的s﹣t图象如图乙所示,则铝块受到的摩擦力大小为 N;若克服摩擦力所做的功全部转化为内能并有44%被铝块吸收,则铝块在10s内的温度升高 ℃.[铝的比热容为c铝=0.88×103J/(kg ℃)]。
12.有一堆从河中捞出的湿砂子,测得其比热容为1.2×103焦/(千克 ℃)。已知干砂子的比热容为0.9×103焦/(千克 ℃),则按质量说,这堆砂子含水的百分比是 %。
13.用两个相同的“热得快”,分别给质量、初温都相同的甲、乙两种液体同时加热,两液体的温度随时间变化关系的图象如图。根据图象可知,甲液体的比热容 乙液体的比热容(选填“大于”、“小于”或“等于”)。如果乙液体是水,那么质量为500g,初温为20℃的乙液体吸收1.89×105J的热量,乙液体的温度升高了 ℃(气压为一标准大气压)。
14.如图所示,质量为200g的某液体,比热容是c=2.1×103J/(kg ℃),在均匀放热的条件下凝固成固态物质,且质量不变,则:第20min的内能 (选填“大于”、“小于”或“等于”)第10min的内能;凝固过程中该物质共放热 J;该物质液态与固态的比热容之比为 。
四、实验探究题
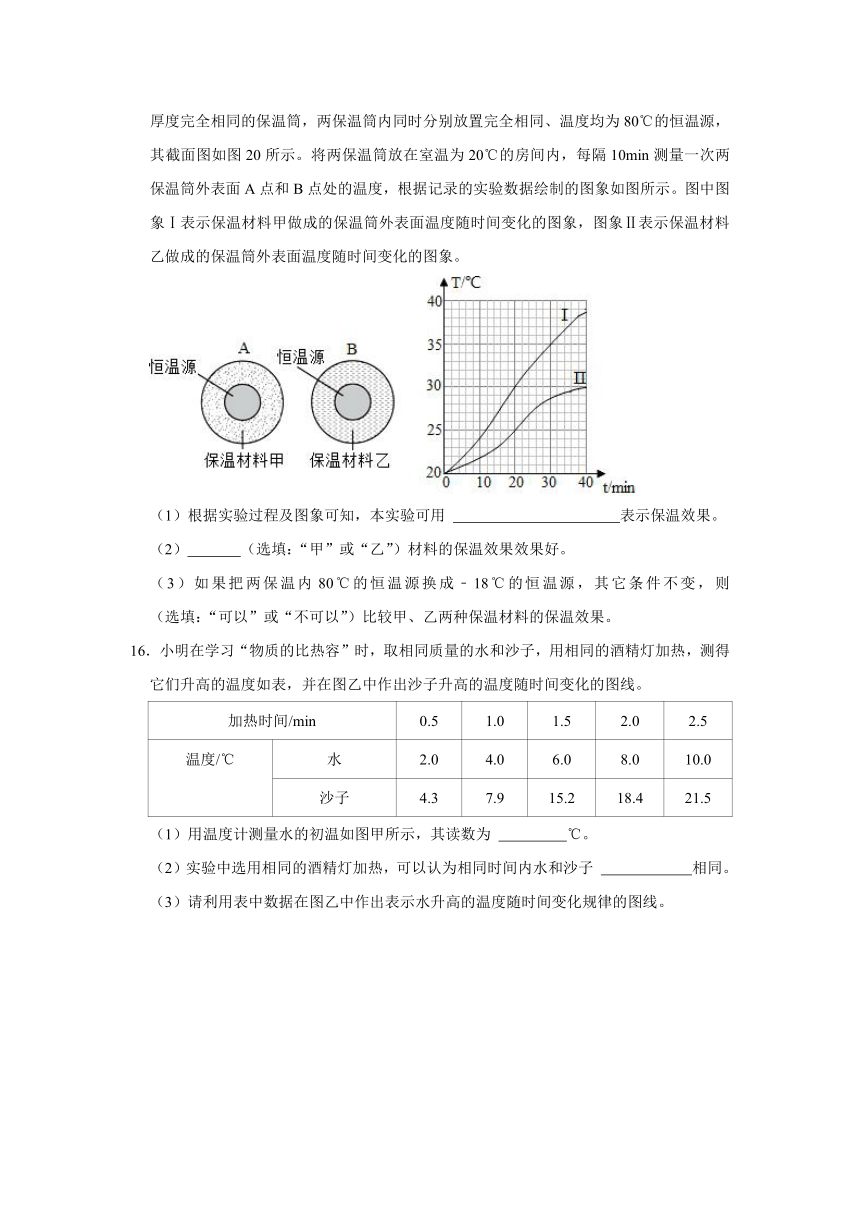
15.为了比较两种新型保温材料甲和乙的保温效果,将这两种保温材料分别做成形状、结构、厚度完全相同的保温筒,两保温筒内同时分别放置完全相同、温度均为80℃的恒温源,其截面图如图20所示。将两保温筒放在室温为20℃的房间内,每隔10min测量一次两保温筒外表面A点和B点处的温度,根据记录的实验数据绘制的图象如图所示。图中图象Ⅰ表示保温材料甲做成的保温筒外表面温度随时间变化的图象,图象Ⅱ表示保温材料乙做成的保温筒外表面温度随时间变化的图象。
(1)根据实验过程及图象可知,本实验可用 表示保温效果。
(2) (选填:“甲”或“乙”)材料的保温效果效果好。
(3)如果把两保温内80℃的恒温源换成﹣18℃的恒温源,其它条件不变,则 (选填:“可以”或“不可以”)比较甲、乙两种保温材料的保温效果。
16.小明在学习“物质的比热容”时,取相同质量的水和沙子,用相同的酒精灯加热,测得它们升高的温度如表,并在图乙中作出沙子升高的温度随时间变化的图线。
加热时间/min 0.5 1.0 1.5 2.0 2.5
温度/℃ 水 2.0 4.0 6.0 8.0 10.0
沙子 4.3 7.9 15.2 18.4 21.5
(1)用温度计测量水的初温如图甲所示,其读数为 ℃。
(2)实验中选用相同的酒精灯加热,可以认为相同时间内水和沙子 相同。
(3)请利用表中数据在图乙中作出表示水升高的温度随时间变化规律的图线。
(4)小明再用50g水和100g水做实验,以吸收的热量Q为纵坐标,升高的温度Δt为横坐标,分别画出50g水和100g水的Q﹣Δt图象,它们都是过原点的直线,即Q=kΔt.进一步分析,发现这两条直线的k值之比与对应水的 之比相等。
17.根据能量转化与守恒定律,在与外界没有热传递的条件下,物体内能的增加量与外界对物体做功多少相等。为了验证此规律,某兴趣小组设计了如图所示的实验,在容器里装一定质量的水,中间装上带有叶片的转轴,转轴上绕上绳子,绳子另一端通过滑轮与一重物相连,当重物下降时,绳子拉动转轴转动,带动叶片旋转,使容器里的水温度升高,结合水的比热计算出水中增加的内能。以此验证水的内能增加量与重物的重力做功多少是否相等。
(1)为了完成此实验,除已提供质量的电子天平外,还需要的测量工具有 。
(2)兴趣小组在实验过程中发现,水内能的增加量小于重物做功的大小,请写出造成这种现象的一种原因 。
(3)改进实验后,获得那如表数据,规律得到验证。
实验序号 重物质量(千克) 下降高度(米) 升高温度(℃)
1 20 5 0.5
2 20 10 1.0
3 20 15 1.5
4 10 10 0.5
5 30 10 1.5
6 40 10 2.0
若使容器内相同质量水的温度升高2.5℃,则25千克的重物需下降 米。
五、计算题
18.某太阳能热水器,水容量为100L,该热水器在冬季有效日照时段里,平均每平方米的面积上每小时接收的太阳能约为2.8×106J,若该热水器接收太阳能的有效面积为1.5m2,每天日照时间按8h计算,若这些太阳能能使装满水的热水器中的水温从20℃升高到60℃[水的比热容为4.2×103J/(kg ℃),水的密度为1.0×103kg/m3,求:
(1)热水器中水的质量;
(2)一天内热水器中的水吸收的热量;
(3)热水器在冬季的效率。
19.物理兴趣小组的同学在研究“沙子和水谁的吸热本领大”时,选用了两只完全相同的酒精灯分别给质量都是0.4kg的沙子和水加热。他们绘制出沙子与水的温度随加热时间变化的图像如图所示,a图是沙子吸热升温的图像。那么:
(1)加热满2min时,水吸收了多少热量?
(2)求出沙子的比热容大约是多少?
20.某校科技小组为培养某种热带植物制作了一个小型温室,其内部有一个恒温加热器。当温室外温度为10℃时,温室内温度为22℃;当温室外温度为16℃时,温室内温度为27℃.假定温室内加热器与室内间、室内与室外间的热量传递与温度差成正比。
(1)求该温室中加热器的温度;
(2)为节省能源,科技小组的同学对该温室进行了适当的保温改造,使室内向室外的热传递的热量减少了20%.那么,当户外温度为10℃的情况下,求室内温度。
苏科版九年级上册《12.2 内能 热传递 物质的比热容》2023年同步练习卷
参考答案与试题解析
一、选择题
1.【解答】解:在质量不变的前提下,吸收热量之比为1:2,温度升高之比为2:1,
根据Q=cmΔt计算可知该物体在固态时的比热与液态时的比热之比是1:4。
所以A,B.D错误,C正确。
故选:C。
2.【解答】解:设热水和冷水的温度差为t,
因为质量为m0的一小杯热水倒入盛有质量为m的冷水的保温容器中,使得冷水温度升高了10℃,
所以Q吸=Q放,即cm0(t﹣10℃)=cm×10℃﹣﹣﹣﹣﹣﹣﹣①
又向保温容器中倒入一小杯同质量为m0同温度的热水,水温又上升了6℃,
Q吸=Q放,即cm0(t﹣10℃﹣6℃)=c(m+m0)×6℃﹣﹣﹣﹣﹣﹣﹣②
联立①②可得:m=3m0;
代入①式可得,t=40℃;
如果继续向容器中倒入5杯同样的热水,则由热平衡方程可知:
5m0c(40℃﹣10℃﹣6℃﹣Δt)=(m+2m0)cΔt,
即5m0c(40℃﹣10℃﹣6℃﹣Δt)=(3m0+2m0)cΔt,
解得Δt=12℃。
故选:B。
3.【解答】解:
甲物体吸收的热量Q甲=c甲m甲Δt甲,乙物体吸收的热量Q乙=c乙m乙Δt乙,
由题知,甲、乙两物体吸收相等的热量,即:Q甲=Q乙,
则:c甲m甲Δt甲=c乙m乙Δt乙,
因为甲物体的温度变化量大,即Δt甲>Δt乙,
所以c甲m甲<c乙m乙,
变形可得<,
A、若m甲=m乙,由上式可知>1,则c甲<c乙,故A正确;
B、若c甲=c乙,由上式可知<1,则m甲<m乙,故B正确;
C、若m甲>m乙,由上式可知>>1,则c甲<c乙,故C一定错误;
D、因为c甲m甲<c乙m乙,若c甲<c乙,则有3种可能,即m甲=m乙,或m甲<m乙,或m甲>m乙,故D可能正确。
故选:C。
4.【解答】解:先后将甲、乙两球投入到同一杯水中,水降低的温度相同,水放出的热量相同,
∵由题知,Q吸=Q放,
∴甲、乙两球吸收的热量相同,
而乙球比甲球少升高了Δt,即乙球的末温低;
由上述分析可知,质量相同的甲、乙两球,吸收相同的热量,乙球升高的温度少,所以乙球的比热容大。
故选:B。
5.【解答】解:设热水原来的温度为t0:
冷水吸收的热量:
Q吸=cm(t﹣t1),
∵Q吸=Q放,
∴热水放出的热量:
Q放=c2m(t0﹣t)=cm(t﹣t1),
解得:
t0=,故C正确。
故选:C。
6.【解答】解:由图象知:
A、用相同的加热装置对b、c两种物质加热时,0﹣t2时间内这两种物质吸收的热量相同,b物质升高的温度较大,由公式c=知,b的比热容小于c的比热容,故A错误;
B、t1﹣t2时间内物质a的温度不变(处于沸腾过程中),但质量减少,所以其内能减少,故B错误;
C、用相同的加热装置,温度从T1升高到T2时,a物质的加热时间比b物质短,所以a物质吸收的热量比b少,故C错误;
D、如果a、b是同种物质,比热容相同,升高相同的温度时,b的加热时间长,说明b吸收的热量多,根据Q=cmΔt知,b的质量大于a的质量,故D正确。
故选:D。
7.【解答】解:
①热水放出的热量:Q放=cm(t0﹣t),冷水吸收的热量:Q吸=cm(t﹣t0);
②假设热水放出的热量全部被凉水吸收,
所以Q吸=Q放,
即4.2×103J/(kg ℃)×0.2kg×(100℃﹣t1)=4.2×103J/(kg ℃)×0.3kg×(t1﹣20℃);
解得t1=52℃。
③速将200g室温矿泉水倒入该杯,摇一摇,矿泉水的温度可升至t2,
即4.2×103J/(kg ℃)×0.3kg×(52℃﹣t2)=4.2×103J/(kg ℃)×0.2kg×(t2﹣20℃);
解得t2=39.2℃。
故选:B。
8.【解答】解:设冷水的温度为t0,甲投入冷水后放热Q放=C甲m(100℃﹣10℃﹣t0),水吸收的热量为Q吸=C水m水10℃,
不考虑热传递过程热量的损失,则有Q放=Q吸,
c甲m(100℃﹣10℃﹣t0)=c水m水10℃,
即:=﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
乙投入冷水后放热Q放′=C乙m(100℃﹣10℃﹣10℃﹣t0),水吸收的热量仍为Q吸=C水m水10℃,
同理则有:=﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②
同时投入后,假设冷水先和甲热交换,而乙温度不变,这样水温上升10℃,达到t1;然后再与乙热交换,水温又上升10℃,达到t2.而此时甲的温度t1小于水和乙的温度t2,会吸收热量,所以温度在上升20℃的基础上必然要下降一点。
故选:A。
二、多选题
9.【解答】解:对于甲和乙,吸收的热量相等,m甲=m乙,Δt甲<Δt乙,根据c=,可得出:甲乙比热容关系为:c甲>c乙。
对于乙和丙,m乙>m丙,Δt乙=Δt丙,Q丙>Q乙,根据c=,可得出:乙丙比热容关系为:c丙>c乙。
由此可得:乙的比热容最小。
已知Δt甲<Δt乙,由于甲、乙的初温关系不确定,所末温的大小关系不确定。
若三个物体的温度都降低1℃,即Δt相同,根据公式Q吸=cmΔt,由于c甲>c乙,m甲=m乙,Δt相同,可得出甲放出的热量比乙多;由图象可知,乙和丙升高相同温度时,丙吸收的热量多,所以,当乙和丙降低相同温度(均为1℃)时,丙放出的热量比乙多。可见,甲放出的热量比乙多,丙放出的热量比乙多,即乙放出的热量最少。
故BC错误,AD正确。
故选:AD。
三、填空题
10.【解答】解:用水来冷却热牛奶,是通过热传递的方法改变内能的;
用水来冷却牛奶,热牛奶的温度是逐渐降低的,所以热牛奶温度随时间变化的曲线应是Ⅰ;
A点温度为18℃,它是牛奶和水混合后的共同温度;
这个过程中水吸收的热量:
Q吸=c水m水(t﹣t0)=4.2×103J/(kg ℃)×m×(18℃﹣10℃)=5.04×104J;
解得m=1.5kg。
故答案为:热传递;Ⅰ;1.5。
11.【解答】解:∵铝块在水平地面上匀速运动,
∴铝块受到的摩擦力:f=F=20N,
由图可知:铝块在10s内通过的路程为50cm,
则铝块克服摩擦阻力做功:
W=Fs=20N×0.5m=10J,
铝块的内能增加值:
Q=W×44%=10J×44%=4.4J,
由Q=cmΔt得:
Δt===0.001℃。
故答案为:20;0.001。
12.【解答】解:m1﹣干砂子的质量,m2﹣水的质量,m﹣砂子和水的混合物的质量;
c1﹣干砂子的比热容,c2﹣水的比热容,c﹣砂子和水的混合物的比热容;Q1﹣干砂子吸收的热量,Q2﹣水吸收的热量,Q﹣砂子和水的混合物吸收的热量;
Δt﹣温度差。
砂子和水的混合物、砂子、水各自吸收的热量可以表示为:
Q=c(m1+m2)Δt (1)
Q1=c1m1Δt (2)
Q2=c2m2Δt (3)
由这三个式子可以解出
=;
代入数值可得:×100%=×100%=9.1%。
故答案为:9.1。
13.【解答】解:
(1)由图象可以看出:在相等时间内,液体甲温度变化量大,则甲液体温度升高较快;而两个加热器相同、加热时间相等时,两种液体吸收的热量相等,由公式Q吸=mcΔt可知,在质量相等、初温相同、吸热也相同的情况下,温度升高快的液体比热容小,所以甲的比热容小于乙的比热容;
(2)根据Q吸=cm(t﹣t0)得:
t=+t0=+20℃=110℃,
因为一标准大气压下,水的沸点为100℃,
所以乙液体的温度升高到100℃后温度不变,
Δt=100℃﹣20℃=80℃。
故答案为:小于;80。
14.【解答】解:
(1)由凝固图象可知,该物质在凝固时温度保持0℃不变,物质在凝固时,放出热量、内能变小,所以第20min的内能小于第10min的内能;
(2)由图象可知,物质从A点降温到B点时,用了5min,温度降低了10℃,
所以,此过程中放出的热量Q放=c液mΔt=2.1×103J/(kg ℃)×0.2kg×10℃=4.2×103J;
因该物质是均匀放热,且质量不变,
所以,相同时间内,物质放出的热量相等,
故凝固过程用了20min,故放出热量为Q凝固放=4×4.2×103J=1.68×104J;
由图象知,液态降温10℃和固态降温20℃所用的时间相等,所以它们放出的热量相等,因为固态段和液态段物质的质量m相同,由图象知,放热时间相同,即热量相同,液态段降温是10℃,固态段降温是20℃,从而计算得比热容之比为:
====2:1。
故答案为:小于;1.68×104;2:1。
四、实验探究题
15.【解答】解:(1)由图知在相等时间内,乙的温度升高的少,乙材料的保温性能好,故可用单位时间内保温筒外表面的温度变化表示保温效果;
(2)由(1)分析可知,在相等时间内,乙的温度升高的少,乙材料的保温性能好;
(3)如果把两保温筒内80℃的恒温源换成﹣18℃的恒温源,其它条件不变,可以通过相同时间,升高的温度多少来比较甲、乙两种保温材料的保温效果。
故答案为:(1)单位时间内保温筒外表面的温度变化;(2)乙;(3)可以。
16.【解答】解:(1)由图知:温度计的分度值为1℃;“20”在“10”的上方,液柱最高处在两者之间,所以显示的温度高于0℃,为18℃。
(2)选用了两个相同的酒精灯,分别给水和沙子加热,这样做的目的是使水和沙子在相同时间吸收相同的热量相同;
(3)根据表中数据在表中找出对应的点连线,水升高的温度随时间变化规律的图线如下图所示:
(4)根据Q=cmΔt可知,知Q=kΔt中的k=cm,则有k1=cm1,k2=cm2,
故=,即这两条直线的k值与对应水的质量之比相等。
故答案为:(1)18; (2)吸收的热量;(3)图象如上图;(4)质量。
17.【解答】解:(1)实验中应需要用刻度尺测量重物下降的高度、用温度计水升高的温度;
(2)在实验的过程中,由于滑轮存在摩擦、液体会散热等情况,使得水内能的增加量小于重物做功的大小;
(3)20kg的重物高度下降5m,水温升高0.5℃,即1kg的重物高度下降1m,水温升高0.005℃,则有25kg的重物高度下降1m,水温升高0.125℃,要使水温升高2.5℃,根据比例可知需要下降的高度为20m。
故答案为:(1)刻度尺、温度计;(2)滑轮存在摩擦;(3)20。
五、计算题
18.【解答】解:(1)热水器中水的体积:
V=100L=100dm3=0.1m3,
由ρ=可得,热水器中水的质量:
m=ρV=1.0×103kg/m3×0.1m3=100kg;
(2)一天内热水器中的水吸收的热量:
Q吸=cm(t﹣t0)=4.2×103J/(kg ℃)×100kg×(60℃﹣20℃)=1.68×107J;
(3)一天内热水器接收太阳能的能量:
E=2.8×106J/(m2 h)×1.5m2×8h=3.36×107J,
热水器在冬季的效率:
η=×100%=×100%=50%。
答:(1)热水器中水的质量为100kg;
(2)一天内热水器中的水吸收的热量1.68×107J;
(3)热水器在冬季的效率为50%
19.【解答】解:(1)由题知,沙子和水的质量相等,且沙子的比热容比水小,吸收相同热量时(加热相同时间),由公式Δt=可知,沙子升高的温度多,所以图a表示的是沙子吸热升温的过程。
由b图象可知,加热满2min时,水的温度从20℃上升到70℃,
则加热满2min时水吸收的热量:
Q水吸=c水m水Δt水=4.2×103J/(kg ℃)×0.4kg×(70℃﹣20℃)=8.4×104J。
(2)相同时间内酒精灯燃烧放出相同的热量,
在2分钟的时间内,沙子吸收的热量:Q沙吸=Q水吸=8.4×104J,
又因为加热满2min,沙子的温度从20℃上升到250℃,
Δt沙=250℃﹣20℃=230℃,m沙=0.4kg,
由Q吸=cmΔt可得,沙子的比热容:
c沙==≈913J/(kg ℃)。
故答案为:(1)加热满2min时,水吸收了8.4×104J热量;
(2)沙子的比热容为913J/(kg ℃)。
20.【解答】解:(1)设加热器的温度为t,温室内加热器与室内传递的热量与温度差的比例系数为k1,室内与室外间传递的热量与温度差的比例系数为k2,
第一种情况为:k1(t﹣22℃)=k2(22℃﹣10℃)﹣﹣﹣﹣﹣①
第二种情况为:k1(t﹣27℃)=k2(27℃﹣16℃)﹣﹣﹣﹣﹣②
①÷②得,t=82℃,=;
(2)设室内温度为t1,则有k1(82℃﹣t1)=k2(t1﹣10℃)(1﹣20%),
解得室内温度:t1=24.4℃。
答:(1)该温室中加热器的温度为82℃;
(2)为节省能源,科技小组的同学对该温室进行了适当的保温改造,使室内向室外的热传递的热量减少了20%.那么,当户外温度为10℃的情况下,室内温度为24.4℃。
一、选择题
1.用稳定的热源给一个物体均匀加热,设物体吸收的热量与加热时间成正比,得到其温度随时间变化的曲线如图所示,那么它在固态时的比热与液态时的比热之比是( )
A.1:2 B.2:1 C.1:4 D.4:1
2.将一杯热水倒入盛有冷水的容器中,冷水的温度升高了10℃,再向容器内倒入一杯相同质量和温度的热水,容器中的水温又升高了6℃。如果继续向容器中倒入5杯同样的热水,则容器中的水温会升高(不计热量损失)( )
A.14℃ B.12℃ C.9℃ D.4℃
3.甲、乙两物体吸收相等热量后,甲物体的温度变化量大。如甲物体的比热容为c甲,质量为m甲,乙物体比热容为c乙,质量是m乙,则下列说法中,一定错误的是( )
A.若m甲=m乙,则c甲<c乙 B.若c甲=c乙,则m甲<m乙
C.若m甲>m乙,则c甲>c乙 D.若c甲<c乙,则m甲<m乙
4.有两个温度和质量都相同的金属球,先把甲球放入盛有热水的杯中,热平衡后水温降低了Δt.把甲球取出,再将乙球放入杯中,热平衡后水温又降低了Δt,则甲球比热c甲和乙球比热c乙大小的关系是( )
A.c甲>c乙 B.c甲<c乙
C.c甲=c乙 D.以上三种情况都有可能
5.冷水的质量为m,温度为t1,吸收一定热量后,温度升高到t;另有质量为2m的热水,如果先放出同样热量后温度也降到t,那么热水原来的温度应是( )
A. B. C. D.
6.如图是用相同的加热装置对a、b、c(已知质量关系为mb=mc)三种物质加热至沸腾时,它们的温度随时间变化的图象。下列对图象的分析正确的是( )
A.b的比热容大于c的比热容
B.t1﹣t2时间内物质a的温度不变,内能不变
C.温度从T1升高到T2时,a物质吸收的热量比b多
D.如果a、b是同种物质,b的质量大于a的质量
7.网上曾热销一时的“55度杯”,称“能很快将开水变成适饮的温水,而后又能将凉水变成适饮的温水”。为破解此中秘密,某同学设计了如图乙模型。设此杯内胆中被封存着300g水,室温20℃;现向杯中倒入200g、100℃开水,摇一摇,杯内水温迅速降至t1,饮用后迅速将200g室温矿泉水倒入该杯,摇一摇,矿泉水的温度可升至t2,若忽略内胆及空间的热能消耗,则t1,t2分别大约为( )
A.50℃50℃ B.52℃39.2℃ C.40℃60℃ D.55℃55℃
8.质量相等的甲、乙两金属块,其材质不同。将它们放入沸水中,一段时间后温度均达到100℃,然后将它们按不同的方式投入一杯冷水中,使冷水升温。第一种方式:先从沸水中取出甲,将其投入冷水,当达到热平衡后将甲从杯中取出,测得水温升高10℃;然后将乙从沸水中取出投入这杯水中,再次达到热平衡,测得水温又升高了10℃.第二种方式:从沸水中取出甲、乙投入冷水,使之达到热平衡。则在第二种方式下,这杯冷水温度的变化是( )
A.升高不足20℃ B.升高超过20℃
C.恰好升高了20℃ D.条件不足,无法判断
二、多选题
(多选)9.甲、乙、丙三个物体的质量关系为m甲=m乙>m丙,当其吸收热量情况如图所示时,升高的温度关系为Δt甲<Δt乙=Δt丙,则关于这三个物体,下列说法正确的是( )
A.乙的比热容最小
B.甲、乙的比热容相等
C.甲、乙的末温一定相等
D.若三个物体的温度都降低1℃,乙放出的热量最少
三、填空题
10.如题图甲所示是用水来冷却热牛奶的示意图。这是用 的方法改变物体内能的,图乙是记录牛奶、水的温度随时间变化的图象,图中曲线I表示的是 的温度随时间变化的情况,若在这个过程中水吸收的热量是5.04×104J,水的质量为 kg.(c水=4.2×103J/(kg ℃))
11.如图甲所示,用20N的水平拉力拉着质量为5kg的铝块在水平地面上运动,铝块运动的s﹣t图象如图乙所示,则铝块受到的摩擦力大小为 N;若克服摩擦力所做的功全部转化为内能并有44%被铝块吸收,则铝块在10s内的温度升高 ℃.[铝的比热容为c铝=0.88×103J/(kg ℃)]。
12.有一堆从河中捞出的湿砂子,测得其比热容为1.2×103焦/(千克 ℃)。已知干砂子的比热容为0.9×103焦/(千克 ℃),则按质量说,这堆砂子含水的百分比是 %。
13.用两个相同的“热得快”,分别给质量、初温都相同的甲、乙两种液体同时加热,两液体的温度随时间变化关系的图象如图。根据图象可知,甲液体的比热容 乙液体的比热容(选填“大于”、“小于”或“等于”)。如果乙液体是水,那么质量为500g,初温为20℃的乙液体吸收1.89×105J的热量,乙液体的温度升高了 ℃(气压为一标准大气压)。
14.如图所示,质量为200g的某液体,比热容是c=2.1×103J/(kg ℃),在均匀放热的条件下凝固成固态物质,且质量不变,则:第20min的内能 (选填“大于”、“小于”或“等于”)第10min的内能;凝固过程中该物质共放热 J;该物质液态与固态的比热容之比为 。
四、实验探究题
15.为了比较两种新型保温材料甲和乙的保温效果,将这两种保温材料分别做成形状、结构、厚度完全相同的保温筒,两保温筒内同时分别放置完全相同、温度均为80℃的恒温源,其截面图如图20所示。将两保温筒放在室温为20℃的房间内,每隔10min测量一次两保温筒外表面A点和B点处的温度,根据记录的实验数据绘制的图象如图所示。图中图象Ⅰ表示保温材料甲做成的保温筒外表面温度随时间变化的图象,图象Ⅱ表示保温材料乙做成的保温筒外表面温度随时间变化的图象。
(1)根据实验过程及图象可知,本实验可用 表示保温效果。
(2) (选填:“甲”或“乙”)材料的保温效果效果好。
(3)如果把两保温内80℃的恒温源换成﹣18℃的恒温源,其它条件不变,则 (选填:“可以”或“不可以”)比较甲、乙两种保温材料的保温效果。
16.小明在学习“物质的比热容”时,取相同质量的水和沙子,用相同的酒精灯加热,测得它们升高的温度如表,并在图乙中作出沙子升高的温度随时间变化的图线。
加热时间/min 0.5 1.0 1.5 2.0 2.5
温度/℃ 水 2.0 4.0 6.0 8.0 10.0
沙子 4.3 7.9 15.2 18.4 21.5
(1)用温度计测量水的初温如图甲所示,其读数为 ℃。
(2)实验中选用相同的酒精灯加热,可以认为相同时间内水和沙子 相同。
(3)请利用表中数据在图乙中作出表示水升高的温度随时间变化规律的图线。
(4)小明再用50g水和100g水做实验,以吸收的热量Q为纵坐标,升高的温度Δt为横坐标,分别画出50g水和100g水的Q﹣Δt图象,它们都是过原点的直线,即Q=kΔt.进一步分析,发现这两条直线的k值之比与对应水的 之比相等。
17.根据能量转化与守恒定律,在与外界没有热传递的条件下,物体内能的增加量与外界对物体做功多少相等。为了验证此规律,某兴趣小组设计了如图所示的实验,在容器里装一定质量的水,中间装上带有叶片的转轴,转轴上绕上绳子,绳子另一端通过滑轮与一重物相连,当重物下降时,绳子拉动转轴转动,带动叶片旋转,使容器里的水温度升高,结合水的比热计算出水中增加的内能。以此验证水的内能增加量与重物的重力做功多少是否相等。
(1)为了完成此实验,除已提供质量的电子天平外,还需要的测量工具有 。
(2)兴趣小组在实验过程中发现,水内能的增加量小于重物做功的大小,请写出造成这种现象的一种原因 。
(3)改进实验后,获得那如表数据,规律得到验证。
实验序号 重物质量(千克) 下降高度(米) 升高温度(℃)
1 20 5 0.5
2 20 10 1.0
3 20 15 1.5
4 10 10 0.5
5 30 10 1.5
6 40 10 2.0
若使容器内相同质量水的温度升高2.5℃,则25千克的重物需下降 米。
五、计算题
18.某太阳能热水器,水容量为100L,该热水器在冬季有效日照时段里,平均每平方米的面积上每小时接收的太阳能约为2.8×106J,若该热水器接收太阳能的有效面积为1.5m2,每天日照时间按8h计算,若这些太阳能能使装满水的热水器中的水温从20℃升高到60℃[水的比热容为4.2×103J/(kg ℃),水的密度为1.0×103kg/m3,求:
(1)热水器中水的质量;
(2)一天内热水器中的水吸收的热量;
(3)热水器在冬季的效率。
19.物理兴趣小组的同学在研究“沙子和水谁的吸热本领大”时,选用了两只完全相同的酒精灯分别给质量都是0.4kg的沙子和水加热。他们绘制出沙子与水的温度随加热时间变化的图像如图所示,a图是沙子吸热升温的图像。那么:
(1)加热满2min时,水吸收了多少热量?
(2)求出沙子的比热容大约是多少?
20.某校科技小组为培养某种热带植物制作了一个小型温室,其内部有一个恒温加热器。当温室外温度为10℃时,温室内温度为22℃;当温室外温度为16℃时,温室内温度为27℃.假定温室内加热器与室内间、室内与室外间的热量传递与温度差成正比。
(1)求该温室中加热器的温度;
(2)为节省能源,科技小组的同学对该温室进行了适当的保温改造,使室内向室外的热传递的热量减少了20%.那么,当户外温度为10℃的情况下,求室内温度。
苏科版九年级上册《12.2 内能 热传递 物质的比热容》2023年同步练习卷
参考答案与试题解析
一、选择题
1.【解答】解:在质量不变的前提下,吸收热量之比为1:2,温度升高之比为2:1,
根据Q=cmΔt计算可知该物体在固态时的比热与液态时的比热之比是1:4。
所以A,B.D错误,C正确。
故选:C。
2.【解答】解:设热水和冷水的温度差为t,
因为质量为m0的一小杯热水倒入盛有质量为m的冷水的保温容器中,使得冷水温度升高了10℃,
所以Q吸=Q放,即cm0(t﹣10℃)=cm×10℃﹣﹣﹣﹣﹣﹣﹣①
又向保温容器中倒入一小杯同质量为m0同温度的热水,水温又上升了6℃,
Q吸=Q放,即cm0(t﹣10℃﹣6℃)=c(m+m0)×6℃﹣﹣﹣﹣﹣﹣﹣②
联立①②可得:m=3m0;
代入①式可得,t=40℃;
如果继续向容器中倒入5杯同样的热水,则由热平衡方程可知:
5m0c(40℃﹣10℃﹣6℃﹣Δt)=(m+2m0)cΔt,
即5m0c(40℃﹣10℃﹣6℃﹣Δt)=(3m0+2m0)cΔt,
解得Δt=12℃。
故选:B。
3.【解答】解:
甲物体吸收的热量Q甲=c甲m甲Δt甲,乙物体吸收的热量Q乙=c乙m乙Δt乙,
由题知,甲、乙两物体吸收相等的热量,即:Q甲=Q乙,
则:c甲m甲Δt甲=c乙m乙Δt乙,
因为甲物体的温度变化量大,即Δt甲>Δt乙,
所以c甲m甲<c乙m乙,
变形可得<,
A、若m甲=m乙,由上式可知>1,则c甲<c乙,故A正确;
B、若c甲=c乙,由上式可知<1,则m甲<m乙,故B正确;
C、若m甲>m乙,由上式可知>>1,则c甲<c乙,故C一定错误;
D、因为c甲m甲<c乙m乙,若c甲<c乙,则有3种可能,即m甲=m乙,或m甲<m乙,或m甲>m乙,故D可能正确。
故选:C。
4.【解答】解:先后将甲、乙两球投入到同一杯水中,水降低的温度相同,水放出的热量相同,
∵由题知,Q吸=Q放,
∴甲、乙两球吸收的热量相同,
而乙球比甲球少升高了Δt,即乙球的末温低;
由上述分析可知,质量相同的甲、乙两球,吸收相同的热量,乙球升高的温度少,所以乙球的比热容大。
故选:B。
5.【解答】解:设热水原来的温度为t0:
冷水吸收的热量:
Q吸=cm(t﹣t1),
∵Q吸=Q放,
∴热水放出的热量:
Q放=c2m(t0﹣t)=cm(t﹣t1),
解得:
t0=,故C正确。
故选:C。
6.【解答】解:由图象知:
A、用相同的加热装置对b、c两种物质加热时,0﹣t2时间内这两种物质吸收的热量相同,b物质升高的温度较大,由公式c=知,b的比热容小于c的比热容,故A错误;
B、t1﹣t2时间内物质a的温度不变(处于沸腾过程中),但质量减少,所以其内能减少,故B错误;
C、用相同的加热装置,温度从T1升高到T2时,a物质的加热时间比b物质短,所以a物质吸收的热量比b少,故C错误;
D、如果a、b是同种物质,比热容相同,升高相同的温度时,b的加热时间长,说明b吸收的热量多,根据Q=cmΔt知,b的质量大于a的质量,故D正确。
故选:D。
7.【解答】解:
①热水放出的热量:Q放=cm(t0﹣t),冷水吸收的热量:Q吸=cm(t﹣t0);
②假设热水放出的热量全部被凉水吸收,
所以Q吸=Q放,
即4.2×103J/(kg ℃)×0.2kg×(100℃﹣t1)=4.2×103J/(kg ℃)×0.3kg×(t1﹣20℃);
解得t1=52℃。
③速将200g室温矿泉水倒入该杯,摇一摇,矿泉水的温度可升至t2,
即4.2×103J/(kg ℃)×0.3kg×(52℃﹣t2)=4.2×103J/(kg ℃)×0.2kg×(t2﹣20℃);
解得t2=39.2℃。
故选:B。
8.【解答】解:设冷水的温度为t0,甲投入冷水后放热Q放=C甲m(100℃﹣10℃﹣t0),水吸收的热量为Q吸=C水m水10℃,
不考虑热传递过程热量的损失,则有Q放=Q吸,
c甲m(100℃﹣10℃﹣t0)=c水m水10℃,
即:=﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
乙投入冷水后放热Q放′=C乙m(100℃﹣10℃﹣10℃﹣t0),水吸收的热量仍为Q吸=C水m水10℃,
同理则有:=﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②
同时投入后,假设冷水先和甲热交换,而乙温度不变,这样水温上升10℃,达到t1;然后再与乙热交换,水温又上升10℃,达到t2.而此时甲的温度t1小于水和乙的温度t2,会吸收热量,所以温度在上升20℃的基础上必然要下降一点。
故选:A。
二、多选题
9.【解答】解:对于甲和乙,吸收的热量相等,m甲=m乙,Δt甲<Δt乙,根据c=,可得出:甲乙比热容关系为:c甲>c乙。
对于乙和丙,m乙>m丙,Δt乙=Δt丙,Q丙>Q乙,根据c=,可得出:乙丙比热容关系为:c丙>c乙。
由此可得:乙的比热容最小。
已知Δt甲<Δt乙,由于甲、乙的初温关系不确定,所末温的大小关系不确定。
若三个物体的温度都降低1℃,即Δt相同,根据公式Q吸=cmΔt,由于c甲>c乙,m甲=m乙,Δt相同,可得出甲放出的热量比乙多;由图象可知,乙和丙升高相同温度时,丙吸收的热量多,所以,当乙和丙降低相同温度(均为1℃)时,丙放出的热量比乙多。可见,甲放出的热量比乙多,丙放出的热量比乙多,即乙放出的热量最少。
故BC错误,AD正确。
故选:AD。
三、填空题
10.【解答】解:用水来冷却热牛奶,是通过热传递的方法改变内能的;
用水来冷却牛奶,热牛奶的温度是逐渐降低的,所以热牛奶温度随时间变化的曲线应是Ⅰ;
A点温度为18℃,它是牛奶和水混合后的共同温度;
这个过程中水吸收的热量:
Q吸=c水m水(t﹣t0)=4.2×103J/(kg ℃)×m×(18℃﹣10℃)=5.04×104J;
解得m=1.5kg。
故答案为:热传递;Ⅰ;1.5。
11.【解答】解:∵铝块在水平地面上匀速运动,
∴铝块受到的摩擦力:f=F=20N,
由图可知:铝块在10s内通过的路程为50cm,
则铝块克服摩擦阻力做功:
W=Fs=20N×0.5m=10J,
铝块的内能增加值:
Q=W×44%=10J×44%=4.4J,
由Q=cmΔt得:
Δt===0.001℃。
故答案为:20;0.001。
12.【解答】解:m1﹣干砂子的质量,m2﹣水的质量,m﹣砂子和水的混合物的质量;
c1﹣干砂子的比热容,c2﹣水的比热容,c﹣砂子和水的混合物的比热容;Q1﹣干砂子吸收的热量,Q2﹣水吸收的热量,Q﹣砂子和水的混合物吸收的热量;
Δt﹣温度差。
砂子和水的混合物、砂子、水各自吸收的热量可以表示为:
Q=c(m1+m2)Δt (1)
Q1=c1m1Δt (2)
Q2=c2m2Δt (3)
由这三个式子可以解出
=;
代入数值可得:×100%=×100%=9.1%。
故答案为:9.1。
13.【解答】解:
(1)由图象可以看出:在相等时间内,液体甲温度变化量大,则甲液体温度升高较快;而两个加热器相同、加热时间相等时,两种液体吸收的热量相等,由公式Q吸=mcΔt可知,在质量相等、初温相同、吸热也相同的情况下,温度升高快的液体比热容小,所以甲的比热容小于乙的比热容;
(2)根据Q吸=cm(t﹣t0)得:
t=+t0=+20℃=110℃,
因为一标准大气压下,水的沸点为100℃,
所以乙液体的温度升高到100℃后温度不变,
Δt=100℃﹣20℃=80℃。
故答案为:小于;80。
14.【解答】解:
(1)由凝固图象可知,该物质在凝固时温度保持0℃不变,物质在凝固时,放出热量、内能变小,所以第20min的内能小于第10min的内能;
(2)由图象可知,物质从A点降温到B点时,用了5min,温度降低了10℃,
所以,此过程中放出的热量Q放=c液mΔt=2.1×103J/(kg ℃)×0.2kg×10℃=4.2×103J;
因该物质是均匀放热,且质量不变,
所以,相同时间内,物质放出的热量相等,
故凝固过程用了20min,故放出热量为Q凝固放=4×4.2×103J=1.68×104J;
由图象知,液态降温10℃和固态降温20℃所用的时间相等,所以它们放出的热量相等,因为固态段和液态段物质的质量m相同,由图象知,放热时间相同,即热量相同,液态段降温是10℃,固态段降温是20℃,从而计算得比热容之比为:
====2:1。
故答案为:小于;1.68×104;2:1。
四、实验探究题
15.【解答】解:(1)由图知在相等时间内,乙的温度升高的少,乙材料的保温性能好,故可用单位时间内保温筒外表面的温度变化表示保温效果;
(2)由(1)分析可知,在相等时间内,乙的温度升高的少,乙材料的保温性能好;
(3)如果把两保温筒内80℃的恒温源换成﹣18℃的恒温源,其它条件不变,可以通过相同时间,升高的温度多少来比较甲、乙两种保温材料的保温效果。
故答案为:(1)单位时间内保温筒外表面的温度变化;(2)乙;(3)可以。
16.【解答】解:(1)由图知:温度计的分度值为1℃;“20”在“10”的上方,液柱最高处在两者之间,所以显示的温度高于0℃,为18℃。
(2)选用了两个相同的酒精灯,分别给水和沙子加热,这样做的目的是使水和沙子在相同时间吸收相同的热量相同;
(3)根据表中数据在表中找出对应的点连线,水升高的温度随时间变化规律的图线如下图所示:
(4)根据Q=cmΔt可知,知Q=kΔt中的k=cm,则有k1=cm1,k2=cm2,
故=,即这两条直线的k值与对应水的质量之比相等。
故答案为:(1)18; (2)吸收的热量;(3)图象如上图;(4)质量。
17.【解答】解:(1)实验中应需要用刻度尺测量重物下降的高度、用温度计水升高的温度;
(2)在实验的过程中,由于滑轮存在摩擦、液体会散热等情况,使得水内能的增加量小于重物做功的大小;
(3)20kg的重物高度下降5m,水温升高0.5℃,即1kg的重物高度下降1m,水温升高0.005℃,则有25kg的重物高度下降1m,水温升高0.125℃,要使水温升高2.5℃,根据比例可知需要下降的高度为20m。
故答案为:(1)刻度尺、温度计;(2)滑轮存在摩擦;(3)20。
五、计算题
18.【解答】解:(1)热水器中水的体积:
V=100L=100dm3=0.1m3,
由ρ=可得,热水器中水的质量:
m=ρV=1.0×103kg/m3×0.1m3=100kg;
(2)一天内热水器中的水吸收的热量:
Q吸=cm(t﹣t0)=4.2×103J/(kg ℃)×100kg×(60℃﹣20℃)=1.68×107J;
(3)一天内热水器接收太阳能的能量:
E=2.8×106J/(m2 h)×1.5m2×8h=3.36×107J,
热水器在冬季的效率:
η=×100%=×100%=50%。
答:(1)热水器中水的质量为100kg;
(2)一天内热水器中的水吸收的热量1.68×107J;
(3)热水器在冬季的效率为50%
19.【解答】解:(1)由题知,沙子和水的质量相等,且沙子的比热容比水小,吸收相同热量时(加热相同时间),由公式Δt=可知,沙子升高的温度多,所以图a表示的是沙子吸热升温的过程。
由b图象可知,加热满2min时,水的温度从20℃上升到70℃,
则加热满2min时水吸收的热量:
Q水吸=c水m水Δt水=4.2×103J/(kg ℃)×0.4kg×(70℃﹣20℃)=8.4×104J。
(2)相同时间内酒精灯燃烧放出相同的热量,
在2分钟的时间内,沙子吸收的热量:Q沙吸=Q水吸=8.4×104J,
又因为加热满2min,沙子的温度从20℃上升到250℃,
Δt沙=250℃﹣20℃=230℃,m沙=0.4kg,
由Q吸=cmΔt可得,沙子的比热容:
c沙==≈913J/(kg ℃)。
故答案为:(1)加热满2min时,水吸收了8.4×104J热量;
(2)沙子的比热容为913J/(kg ℃)。
20.【解答】解:(1)设加热器的温度为t,温室内加热器与室内传递的热量与温度差的比例系数为k1,室内与室外间传递的热量与温度差的比例系数为k2,
第一种情况为:k1(t﹣22℃)=k2(22℃﹣10℃)﹣﹣﹣﹣﹣①
第二种情况为:k1(t﹣27℃)=k2(27℃﹣16℃)﹣﹣﹣﹣﹣②
①÷②得,t=82℃,=;
(2)设室内温度为t1,则有k1(82℃﹣t1)=k2(t1﹣10℃)(1﹣20%),
解得室内温度:t1=24.4℃。
答:(1)该温室中加热器的温度为82℃;
(2)为节省能源,科技小组的同学对该温室进行了适当的保温改造,使室内向室外的热传递的热量减少了20%.那么,当户外温度为10℃的情况下,室内温度为24.4℃。
同课章节目录
- 第十一章 简单机械和功
- 1 杠杆
- 2 滑轮
- 3 功
- 4 功率
- 5 机械效率
- 第十二章 机械能和内能
- 1 动能 势能 机械能
- 2 内能 热传递
- 3 物质的比热容
- 4 机械能和内能的相互转化
- 第十三章 电路初探
- 1 初识家用电器和电路
- 2 电路连接的基本方式
- 3 电流和电流表的使用
- 4 电压和电压表的使用
- 第十四章 欧姆定律
- 1 电阻
- 2 变阻器
- 3 欧姆定律
- 4 欧姆定律的应用
- 第十五章 电功和电热
- 电能表与电功
- 电功率
- 电热器 电流的热效应
- 家庭电路与安全用电
- 第十六章 电磁转换
- 磁体与磁场
- 电流的磁场
- 磁场对电流的作用 电动机
- 安装直流电动机模型
- 电磁感应 发电机
- 第十七章 电磁波与现代通信
- 信息与信息传播
- 电磁波及其传播
- 现代通信 走进信息时代
- 第十八章 能源与可持续发展
- 能源利用与社会发展
- 核能
- 太阳能
- 能量转化的基本规律
- 能源与可持续发展
