人教版数学7年级下册 第五章 相交线与平行线 小结学案(含答案)
文档属性
| 名称 | 人教版数学7年级下册 第五章 相交线与平行线 小结学案(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 80.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 09:04:52 | ||
图片预览

文档简介
小结
班级:_____________姓名:__________________组号:_________
相交线与平行线复习(2)
一、知识梳理
(一)平行线判定与性质:
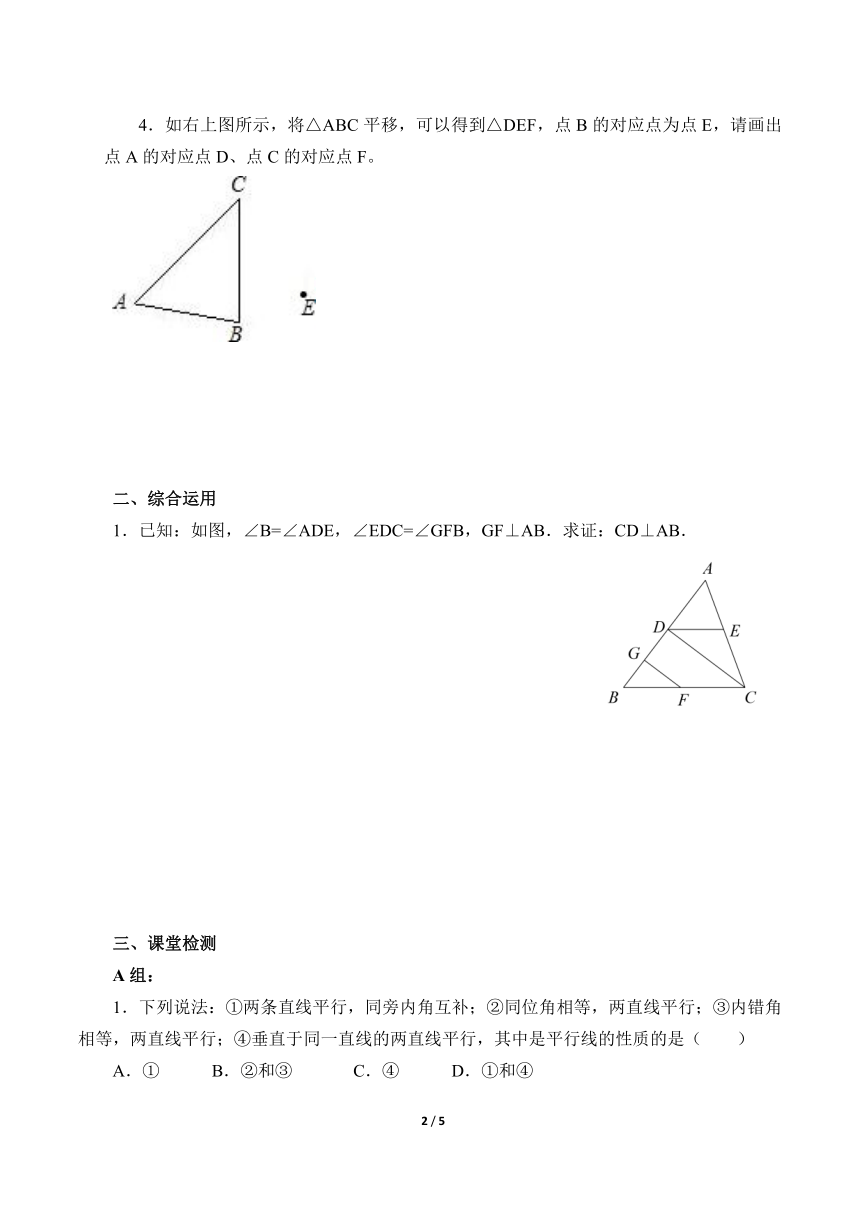
1.如图所示,(1)如果∠1= ,那么AB∥EF;
(2)如果∠1= ,那么DF∥AC;
(3)如果∠DEC+ =180°,那么DE∥BC.
2.如图所示,若AB∥DC,∠1=39°,∠C和∠D互余,
则∠D= ,∠B= 。
3.已知:如图,AB∥CD,EF分别交于AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD。求证:EG∥FH。
证明:∵AB∥CD(已知),
∴∠AEF=∠EFD.( )
∵EG平分∠AEF,FH平分∠EFD.( )
∴∠ =∠AEF,
∠ =∠EFD,( )
∴∠ =∠ 。
∴EG∥FH。( )
归纳:平行线判定与性质的有何区别:
(二)动手操作:
4.如右上图所示,将△ABC平移,可以得到△DEF,点B的对应点为点E,请画出点A的对应点D、点C的对应点F。
二、综合运用
1.已知:如图,∠B=∠ADE,∠EDC=∠GFB,GF⊥AB.求证:CD⊥AB.
三、课堂检测
A组:
1.下列说法:①两条直线平行,同旁内角互补;②同位角相等,两直线平行;③内错角相等,两直线平行;④垂直于同一直线的两直线平行,其中是平行线的性质的是( )
A.① B.②和③ C.④ D.①和④
B组:
2.如图,∠ABC和∠ACB的平分线BO与CO相交于点O,EF过点O,且EF∥BC,若∠BOC=130°,∠ABC∶∠ACB=3∶2,则∠AEF=________,∠EFC=_________。
四、课堂小结
通过本节课的复习,你学到了哪些?还有哪些困惑?
五、拓展延伸(选做题)
1.已知:如图,AB∥DE,CM平分∠BCE,CN⊥CM。求证:∠B=2∠DCN。
【答案】
【知识梳理】
1.(1)∠A
(2)∠2
(3)∠C
2.39° 129°
3.证明:∵AB∥CD(已知),
∴∠AEF=∠EFD.(两直线平行,内错角相等)
∵EG平分∠AEF,FH平分∠EFD.( 已知 )
∴ ∠ GEF =∠AEF,
∠ HFE =∠EFD,(角平分线定义)
∴∠ GEF =∠ HFE 。
∴EG∥FH。(内错角相等,两直线平行)
归纳:判定是由已知角的关系得到平行,性质是先有平行再得到角的关系
4.
【综合运用】
1.证明:∵∠B=∠ADE,
∴DE∥BC,
∴∠EDC=∠DCF,
∵∠EDC=∠GFB,
∴∠DCF=∠GFB,
∴CD∥GF,
∴∠CDG=∠FGB,
∵GF⊥AB
∴∠CDG=∠FGB=90°,
∴CD⊥AB
课堂检测
1.A
2.60° 140°
课堂小结
略
拓展延伸
证明:∵AB∥DE,
∴∠B+∠BCE=180°,∠B=∠BCD,
∵CM平分∠BCE,
∴∠1=∠2,
∵CN⊥CM,
∴∠2+∠3=90°,∠1+∠4=90°,
∴∠3=∠4,
∵∠3+∠4=∠BCD,
∴∠B=2∠DCN。
完成情况
复习导航:阅读书P34-35,带着书中的问题进行复习思考。
5 / 5
班级:_____________姓名:__________________组号:_________
相交线与平行线复习(2)
一、知识梳理
(一)平行线判定与性质:
1.如图所示,(1)如果∠1= ,那么AB∥EF;
(2)如果∠1= ,那么DF∥AC;
(3)如果∠DEC+ =180°,那么DE∥BC.
2.如图所示,若AB∥DC,∠1=39°,∠C和∠D互余,
则∠D= ,∠B= 。
3.已知:如图,AB∥CD,EF分别交于AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD。求证:EG∥FH。
证明:∵AB∥CD(已知),
∴∠AEF=∠EFD.( )
∵EG平分∠AEF,FH平分∠EFD.( )
∴∠ =∠AEF,
∠ =∠EFD,( )
∴∠ =∠ 。
∴EG∥FH。( )
归纳:平行线判定与性质的有何区别:
(二)动手操作:
4.如右上图所示,将△ABC平移,可以得到△DEF,点B的对应点为点E,请画出点A的对应点D、点C的对应点F。
二、综合运用
1.已知:如图,∠B=∠ADE,∠EDC=∠GFB,GF⊥AB.求证:CD⊥AB.
三、课堂检测
A组:
1.下列说法:①两条直线平行,同旁内角互补;②同位角相等,两直线平行;③内错角相等,两直线平行;④垂直于同一直线的两直线平行,其中是平行线的性质的是( )
A.① B.②和③ C.④ D.①和④
B组:
2.如图,∠ABC和∠ACB的平分线BO与CO相交于点O,EF过点O,且EF∥BC,若∠BOC=130°,∠ABC∶∠ACB=3∶2,则∠AEF=________,∠EFC=_________。
四、课堂小结
通过本节课的复习,你学到了哪些?还有哪些困惑?
五、拓展延伸(选做题)
1.已知:如图,AB∥DE,CM平分∠BCE,CN⊥CM。求证:∠B=2∠DCN。
【答案】
【知识梳理】
1.(1)∠A
(2)∠2
(3)∠C
2.39° 129°
3.证明:∵AB∥CD(已知),
∴∠AEF=∠EFD.(两直线平行,内错角相等)
∵EG平分∠AEF,FH平分∠EFD.( 已知 )
∴ ∠ GEF =∠AEF,
∠ HFE =∠EFD,(角平分线定义)
∴∠ GEF =∠ HFE 。
∴EG∥FH。(内错角相等,两直线平行)
归纳:判定是由已知角的关系得到平行,性质是先有平行再得到角的关系
4.
【综合运用】
1.证明:∵∠B=∠ADE,
∴DE∥BC,
∴∠EDC=∠DCF,
∵∠EDC=∠GFB,
∴∠DCF=∠GFB,
∴CD∥GF,
∴∠CDG=∠FGB,
∵GF⊥AB
∴∠CDG=∠FGB=90°,
∴CD⊥AB
课堂检测
1.A
2.60° 140°
课堂小结
略
拓展延伸
证明:∵AB∥DE,
∴∠B+∠BCE=180°,∠B=∠BCD,
∵CM平分∠BCE,
∴∠1=∠2,
∵CN⊥CM,
∴∠2+∠3=90°,∠1+∠4=90°,
∴∠3=∠4,
∵∠3+∠4=∠BCD,
∴∠B=2∠DCN。
完成情况
复习导航:阅读书P34-35,带着书中的问题进行复习思考。
5 / 5
